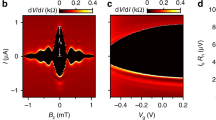
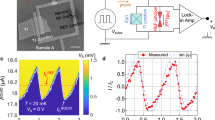
Abstract
Majorana zero modes—quasiparticle states localized at the boundaries of topological superconductors—are expected to be ideal building blocks for fault-tolerant quantum computing1,2. Several observations of zero-bias conductance peaks measured by tunnelling spectroscopy above a critical magnetic field have been reported as experimental indications of Majorana zero modes in superconductor–semiconductor nanowires3,4,5,6,7,8. On the other hand, two-dimensional systems offer the alternative approach of confining Majorana channels within planar Josephson junctions, in which the phase difference φ between the superconducting leads represents an additional tuning knob that is predicted to drive the system into the topological phase at lower magnetic fields than for a system without phase bias9,10. Here we report the observation of phase-dependent zero-bias conductance peaks measured by tunnelling spectroscopy at the end of Josephson junctions realized on a heterostructure consisting of aluminium on indium arsenide. Biasing the junction to φ ≈ π reduces the critical field at which the zero-bias peak appears, with respect to φ = 0. The phase and magnetic-field dependence of the zero-energy states is consistent with a model of Majorana zero modes in finite-size Josephson junctions. As well as providing experimental evidence of phase-tuned topological superconductivity, our devices are compatible with superconducting quantum electrodynamics architectures11 and are scalable to the complex geometries needed for topological quantum computing9,12,13.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
References
Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor–semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Das, A. et al. Zero-bias peaks and splitting in an Al–InAs nanowire topological superconductor as a signature of Majorana fermions. Nat. Phys. 8, 887–895 (2012).
Deng, M. T. et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 354, 1557–1562 (2016).
Suominen, H. J. et al. Zero-energy modes from coalescing Andreev states in a two-dimensional semiconductor–superconductor hybrid platform. Phys. Rev. Lett. 119, 176805 (2017).
Nichele, F. et al. Scaling of Majorana zero-bias conductance peaks. Phys. Rev. Lett. 119, 136803 (2017).
Zhang, H. et al. Quantized Majorana conductance. Nature 556, 74–79 (2018).
Hell, M., Leijnse, M. & Flensberg, K. Two-dimensional platform for networks of Majorana bound states. Phys. Rev. Lett. 118, 107701 (2017).
Pientka, F. et al. Topological superconductivity in a planar Josephson junction. Phys. Rev. X 7, 021032 (2017).
Casparis, L. et al. Superconducting gatemon qubit based on a proximitized two-dimensional electron gas. Nat. Nanotechnol. 13, 915–919 (2018).
Hell, M., Flensberg, K. & Leijnse, M. Coupling and braiding Majorana bound states in networks defined in two-dimensional electron gases with proximity-induced superconductivity. Phys. Rev. B 96, 035444 (2017).
Stern, A. & Berg, E. Fractional Josephson vortices and braiding of Majorana zero modes in planar superconductor–semiconductor heterostructures. Phys. Rev. Lett. 122, 107701 (2019).
Shabani, J. et al. Two-dimensional epitaxial superconductor–semiconductor heterostructures: a platform for topological superconducting networks. Phys. Rev. B 93, 155402 (2016).
Krogstrup, P. et al. Epitaxy of semiconductor–superconductor nanowires. Nat. Mater. 14, 400–406 (2015).
Kjaergaard, M. et al. Quantized conductance doubling and hard gap in a two-dimensional semiconductor–superconductor heterostructure. Nat. Commun. 7, 12841 (2016).
Kjaergaard, M. et al. Transparent semiconductor–superconductor interface and induced gap in an epitaxial heterostructure Josephson junction. Phys. Rev. Appl. 7, 034029 (2017).
Blonder, G. E., Tinkham, M. & Klapwijk, T. M. Transition from metallic to tunneling regimes in superconducting micro-constrictions: excess current, charge imbalance, and supercurrent conversion. Phys. Rev. B 25, 4515–4532 (1982).
Klapwijk, T. M. Proximity effect from an Andreev perspective. J. Supercond. 17, 593–611 (2004).
Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana fermions and a topological phase transition in semiconductor–superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Oreg, Y., Refael, G. & von Oppen, F. Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).
Tinkham, M. Introduction to Superconductivity (Dover, Mineola, 2004).
Andreev, A. F. The thermal conductivity of the intermediate state in superconductors. Sov. Phys. JETP 19, 1228–1231 (1964).
Kulik, I. O. Macroscopic quantization and the proximity effect in S–N–S junctions. Sov. Phys. JETP 30, 944–950 (1970).
Yokoyama, T., Eto, M. & Nazarov, V. Y. Josephson current through semiconductor nanowire with spin–orbit interaction in magnetic field. J. Phys. Soc. Jpn 82, 054703 (2013).
van Woerkom, D. J. et al. Microwave spectroscopy of spinful Andreev bound states in ballistic semiconductor. Nat. Phys. 13, 876–881 (2017).
Haim, A. & Stern, A. The double-edge sword of disorder in multichannel topological superconductors. https://arXiv.org/abs/1808.07886 (2018).
Suominen, H. J. et al. Anomalous Fraunhofer interference in epitaxial superconductor–semiconductor Josephson junctions. Phys. Rev. B 95, 035307 (2017).
Hart, S. et al. Controlled finite momentum pairing and spatially varying order parameter in proximitized HgTe quantum wells. Nat. Phys. 13, 87–93 (2016).
Drachmann, A. C. C. et al. Proximity effect transfer from NbTi into a semiconductor heterostructure via epitaxial aluminum. Nano Lett. 17, 1200–1203 (2017).
Delfanazari, K. et al. On-chip Andreev devices: hard superconducting gap and quantum transport in ballistic Nb–In0.75Ga0.25As-quantum-well–Nb Josephson junctions. Adv. Mater. 29, 1701836 (2017).
Thomas, C. et al. High-mobility InAs 2DEGs on GaSb substrates: a platform for mesoscopic quantum transport. Phys. Rev. Mater. 2, 104602 (2018).
Vurgaftman, I., Meyer, J. R. & Ram-Mohan, L. R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 89, 5815–5875 (2001).
O’Farrell, E. C. T. et al. Hybridization of sub-gap states in one-dimensional superconductor–semiconductor Coulomb islands. Phys. Rev. Lett. 121, 256803 (2018).
Groth, C. W., Wimmer, M., Akhmerov, A. R. & Waintal, X. Kwant: a software package for quantum transport. New J. Phys. 16, 063065 (2014).
Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys. Uspekhi 44, 131 (2001).
Tewari, S. & Sau, J. D. Topological invariants for spin–orbit coupled superconductor nanowires. Phys. Rev. Lett. 109, 150408 (2012).
Beenakker, C. W. J. Quantum transport in semiconductor–superconductor microjunctions. Phys. Rev. B 46, 12841–12844 (1992).
Acknowledgements
This work was supported by Microsoft Corporation, the Danish National Research Foundation, the Villum Foundation, ERC Project MUNATOP, CRC-183 and the Israeli Science Foundation. We thank E. O’Farrell, M. Hell, K. Flensberg and J. Folk for discussions.
Reviewer information
Nature thanks Kaveh Delfanazari and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
S.G., C.T., T.W., R.K., G.C.G. and M.J.M. developed and grew the InAs/Al heterostructure. A.F., A.M.W. and A.C.C.D. fabricated the devices. A.F., A.M.W. and A.C.C.D. performed the measurements with input from C.M.M. and F.N. Data analysis was done by A.F., A.M.W. and E.P.M. F.S., A.K., E.B. and A.S. developed the theoretical model and carried out the simulations. C.M.M. and F.N. conceived the experiment. All authors contributed to interpreting the data. The manuscript was written by A.F., A.M.W., C.M.M. and F.N. with suggestions from all other authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Calculated spectra for a symmetric device.
a, Topological phase diagram as a function of the Zeeman energy \({E}_{{\rm{Z}}}\) and the 2DEG chemical potential µ for two values of the phase bias \(\phi \) = 0, π, calculated from the tight-binding Hamiltonian for JJ1 with infinite length (see Methods) and symmetric superconducting leads. The curves indicate the critical value of \({E}_{{\rm{Z}}}\) above which the system is tuned into the topological phase. b, Topological phase diagram as a function of \({E}_{{\rm{Z}}}\) and \(\phi \) for different values of µ, as indicated by the horizontal ticks in a. The diagrams were calculated for a junction with width W1 = 80 nm, superconducting lead width WS1 = 160 nm, induced gap ∆L,R = 150 µeV and Rashba spin–orbit coupling constant α = 100 meV Å. The length of the junction L1 was assumed to be infinite in order to obtain a well-defined topological invariant, as described in the Methods. c–g, Calculated energy spectra as a function of \(\phi \) for different values of the Zeeman energy. The spectra were obtained for the same parameters used in a and b, except for L1 = 1.6 µm. For this left–right symmetric junction, the topological transition can occur at \({E}_{{\rm{Z}}}\) = 0 for \(\phi \) = π and specific values of chemical potential. We calculate the spectra and Majorana wavefunctions at this fine-tuned chemical potential µ = 79.25 meV (corresponding to the purple curve in b). For the chosen parameters, the system undergoes a topological transition at \({E}_{{\rm{Z}}}\) = 0 for \(\phi \) = π and at \({E}_{{\rm{Z}}}\) = 0.12 meV for \(\phi \) = 0. The lowest-energy subgap states are shown in red and indicate two Majorana zero modes at the edges of the junction in the topological regime. As a function of \({E}_{{\rm{Z}}}\) these states first reach zero energy at \(\phi \) = π and progressively extend in phase. At high values of \({E}_{{\rm{Z}}}\), the Majorana modes oscillate around zero energy owing to their hybridization, caused by the finite size of our system. This is particularly evident at \(\phi \) = π, where the induced gap is minimized and the coherence length is maximized. h, i, Probability density \({\left|\Psi \right|}^{2}\) of the Majorana wavefunction calculated as a function of the spatial directions x and y in JJ1 for \({E}_{{\rm{Z}}}\) = 0.13 meV and \(\phi \) = 0, π. The x coordinate extends in the width direction including the superconducting leads (\(2{W}_{{\rm{S}}1}+{W}_{1}\)) = 0.4 µm, with x = 0 indicating the centre of the junction, while y is the coordinate along the length of the junction. The Majorana wavefunctions are localized in the y direction at the edges of the junction when the lowest energy states in the spectrum are close to zero energy. In the x direction, the Majorana modes are delocalized below the superconducting leads, owing to our geometry having \({W}_{{\rm{S}}1}\ll {\xi }_{{\rm{S}}}\).
Extended Data Fig. 2 Non-symmetric device spectra.
Calculated topological phase diagrams and energy spectra for a left–right asymmetric junction (here the asymmetry is introduced by having ∆L \(\ne \)∆R). As explained in the Methods, the left–right symmetry may be broken by disorder27,28, different geometric sizes of the superconducting leads, or different coupling of the 2DEG to the superconductors on the two sides of the junctions. a, Topological phase diagram as a function of \({E}_{{\rm{Z}}}\) and µ for \(\phi \) = 0, π, calculated from the tight-binding Hamiltonian for JJ1 with infinite length (see Methods). b, Topological phase diagram as a function of \({E}_{{\rm{Z}}}\) and \(\phi \) for different values of µ, as indicated by the horizontal ticks in a. The diagrams were calculated for a junction with W1 = 80 nm, WS1 = 160 nm, left-induced gap ∆L = 150 µeV, right-induced gap ∆R = 100 µeV and α = 100 meV Å. c–g, Calculated energy spectra as a function of \(\phi \) for different values of the Zeeman energy. The spectra were obtained for the same parameters used in a and b, except for L1 = 1.6 µm. Note that the gap for the fine-tuned chemical potential µ = 79.25 meV, which closes at \(\phi \) = π and \({E}_{{\rm{Z}}}\) = 0 for a left–right symmetric junction (see Extended Data Fig. 1a, c), now becomes non-zero, and is approximately \(| {{\Delta }}_{{\rm{L}}}-{{\Delta }}_{{\rm{R}}}\)|. As a result, the topological transition for \(\phi \) = π occurs at finite Zeeman field. For the chosen parameters, the system undergoes a topological transition at \({E}_{{\rm{Z}}}\) = 0.02 meV for \(\phi \) = π and at \({E}_{{\rm{Z}}}\) = 0.1 meV for \(\phi \) = 0. The lowest subgap states are shown in red and indicate two Majorana zero modes at the edges of the junction in the topological regime. The behaviour of the calculated Majorana modes is qualitatively consistent with that of the observed zero-bias peaks in tunnelling conductance. h, i, Probability density \({\left|\Psi \right|}^{2}\) of the Majorana wavefunction calculated as a function of the spatial directions x and y in JJ1 for \({E}_{{\rm{Z}}}\) = 0.13 meV and \(\phi \) = 0, π.
Extended Data Fig. 3 Transport spectroscopy in transverse field for device 1.
a–h, Differential conductance G as a function of the magnetic flux Φ threading the SQUID loop and source–drain bias, Vsd, measured at different values of the transverse magnetic field Bt (applied in plane orthogonally to the junction) in device 1. Several ABSs enter the gap without sticking to zero energy. The induced gap collapses at Bt ≈ 360 mT.
Extended Data Fig. 4 Quantum point contact characterization and stability of the zero-bias peak.
a, G as a function of Vsd and QPC voltage Vqpc at zero field in device 1. b, Differential conductance at zero source–drain bias, G(Vsd = 0 mV), versus averaged differential conductance at finite source–drain bias, G(|Vsd| > 0.4 mV). The green line is the theoretically predicted conductance in an Andreev-enhanced QPC, \({G}_{{\rm{S}}}=2{G}_{0}\frac{{G}_{{\rm{N}}}^{2}}{{\left(2{G}_{0}-{G}_{{\rm{N}}}\right)}^{2}}\) (ref. 38), where \({G}_{{\rm{S}}}\) is the sub-gap conductance, \({G}_{{\rm{N}}}\) is the above-gap conductance and \({G}_{0}=2{e}^{2}/h\) is the quantum of conductance. No fitting parameters have been used. c, G as a function of Vsd and Vqpc at parallel field B|| = 780 mT and \(\phi \) ≈ 0.8π for gate voltages V1 = −110 mV and Vtop = −35 mV. d, G as a function of Vsd and Vtop at B|| = 600 mT and \(\phi \) ≈ 0 for V1 = −118.5 mV and Vqpc = −2.366 mV. In both c and d, the ZBP is robust against variation of the above-gap conductance of about one order of magnitude. e, f, G as a function of Vsd and B||, for different values of \(\phi \) in device 1. The plots have been reconstructed from measurements similar to those shown in Fig. 2 of the main text. For \(\phi \) ≈ π, a ZBP forms at B|| = 0.35 T, whereas for \(\phi \) = 0 it appears at B|| = 575 mT. The ZBP at \(\phi \) ≈ π oscillates and moves away from zero energy as the field is increased.
Extended Data Fig. 5 Tunnelling spectroscopy at lower tunnelling transmission in devices 1 and 2.
a–j, Results obtained for device 1. k–t, Results obtained for device 2. The devices were intended to be lithographically identical. a, c, e, g, i, G as a function of Φ threading the SQUID loop and Vsd measured at different values of B|| in device 1 (W1 = 80 nm). The QPC was tuned to reduce the above-gap conductance by a factor of about 3 with respect to the one measured in the regime presented in the main text. At zero field, the sub-gap conductance is suppressed. Colour extrema have been saturated. b, d, f, h, j, Conductance line cuts versus Vsd taken at \(\phi \) = 0, π, as indicated by red and black ticks in a, c, e, g, i. The grey dashed lines indicate Vsd = 0. k, m, o, q, s, G as a function of Φ threading the SQUID loop and Vsd measured at different values of B|| in device 2 (W1 = 80 nm). Colour extrema have been saturated. l, n, p, r, t, Conductance line cuts versus Vsd taken at phase bias \(\phi \) = 0, π, as indicated by red and black ticks in k, m, o, q, s. The grey dashed lines indicate Vsd = 0.
Extended Data Fig. 6 Measurement of the third harmonic of the current.
a, G as a function of Vsd and Φ at B|| = 850 mT measured with an excitation amplitude Vac = 3 µV in device 1. b, Numerical second derivative of the conductance \(G^{\prime\prime} \left({V}_{{\rm{sd}}}\right){\left.=\left({\partial }^{2}G/\partial {V}^{2}\right)\right|}_{{V}_{{\rm{sd}}}}\) as a function of Vsd and Φ calculated from the data shown in a. c, Third harmonic of the current \({I}_{3\omega }\) versus Vsd and Φ measured by the lock-in amplifier using an excitation Vac = 15 µV, as explained in the Methods. To increase the signal-to-noise ratio, the amplitude of the excitation has been chosen to be greater than the temperature-limited full-width at half-maximum of a Lorentzian feature, that is, Vac ≈ 3.5 kBT, where \({k}_{{\rm{B}}}\) is the Boltzmann constant and T ≈ 40 mK is the electron temperature in our devices. Most of the features present in b are reproduced in c. d, e, Line cuts of G as a function of Vsd taken at \(\phi \) = 0, π as indicated by the ticks in a. f, \({I}_{3\omega }\left({V}_{{\rm{sd}}}=0\right)\) as a function of Φ: a positive value of \({I}_{3\omega }\left({V}_{{\rm{sd}}}=0\right)\) indicates a ZBP in G. See Methods for further details.
Extended Data Fig. 7 Zero-bias peak stability in device 2 (W1 = 80 nm).
a, G as a function of Φ threading the SQUID loop and Vsd measured at different values of B|| in device 2 at V1 = −191 mV. b, Third harmonic of the current \({I}_{3\omega }\left({V}_{{\rm{sd}}}=0\right)\) measured by the lock-in amplifier at zero bias as a function of V1 and Φ for different values of B||. \({I}_{3\omega }\left({V}_{{\rm{sd}}}=0\right)\propto -G^{\prime\prime} \left({V}_{{\rm{sd}}}=0\right)\) \(=-{\left.\left({\partial }^{2}G/\partial {V}^{2}\right)\right|}_{{V}_{{\rm{sd}}}=0}\), as shown in the Methods and Extended Data Fig. 6. A positive value of \({I}_{3\omega }\left({V}_{{\rm{sd}}}=0\right)\) corresponds to a ZBP in conductance as a function of Vsd. As B|| is increased, the ZBP expands in phase and in V1 range, consistent to what is observed in Fig. 3 of the main text for device 1. c, \({I}_{3\omega }\left({V}_{{\rm{sd}}}=0\right)\) measured by the lock-in amplifier at zero bias as a function of B|| and Φ for different values of V1. A positive value of \({I}_{3\omega }\left({V}_{{\rm{sd}}}=0\right)\) corresponds to a ZBP in conductance as a function of Vsd. The critical field at which the ZBP first appear is minimized at φ ≈ π. The behaviour of the ZBP is tuned by V1 and is qualitatively consistent with the topological phase diagrams shown in Extended Data Fig. 2a, b.
Extended Data Fig. 8 Tunnelling spectroscopy in device 3 (W1 = 120 nm).
a–h, G as a function of Φ and Vsd measured at different values of B|| in device 3 (W1 = 120 nm). In this device, spectroscopy was performed with a QPC forming a tunnel barrier between the top edge of JJ1 and a wide planar Al lead, following the approach of refs 6,7. At B|| = 0, the superconducting probe generates a flux-independent gap \({{\Delta }}_{{\rm{p}}{\rm{r}}{\rm{o}}{\rm{b}}{\rm{e}}}^{\ast }\) ≈ 200 µeV added to the junction gap ∆ ≈ 100 µeV, together with the characteristic features of negative differential conductance, as visible in a. When a moderate parallel field is applied, the superconducting gap below the superconducting plane softens, creating a finite density of states at zero energy. This feature allows the Al plane to be used as an effective normal lead that can probe discrete states close to zero energy in the junction. At B|| = 250 mT, we can see a complete phase modulation of ∆, indicating that the Al plane gap is already soft (see b). As the field is increased, two ABSs move towards zero energy, forming a ZBP first localized at phase bias φ ≈ π and then extending up to φ = 0, as shown in c–f. At higher fields, the induced gap collapses (g, h). The lower value of ∆ and critical field compared to that observed in devices 1 and 2 are presumably due to the larger width of the junction.
Extended Data Fig. 9 Behaviour of the Josephson critical current at B|| = 0.
a, To investigate the behaviour of the Josephson current in our device, we measured the differential resistance R = dV/dI of the SQUID with a conventional four-probe technique by applying an a.c. bias Iac < 5 nA, superimposed on a variable d.c. bias Idc, to one of the superconducting leads of the interferometer. During these measurements the QPC was pinched off at Vqpc = −5 V. The Josephson critical current of JJ1 can be measured independently by pinching off JJ2. b, Differential resistance R1 of JJ1 as a function of the Idc and V1 measured in device 2. The region of zero resistance indicates that a dissipationless Josephson current due to Cooper pair transport is flowing through the junction. c, R1 as a function of Idc and the out-of-plane field B⊥ displaying a characteristic Fraunhofer pattern, with a periodicity compatible with the area of JJ1 \({W}_{1}\times {L}_{1}\) ≈ 0.13 µm2. For both the measurements displayed in a and c, JJ2 was pinched off by setting the gate voltage V2 = −1.5 V. d, When JJ2 was open (V2 = 0), the differential resistance of the SQUID RSQUID showed periodic oscillations (periodicity of 250 µT, consistent with the area of the superconducting loop, ∼8 µm2) superimposed to the Fraunhofer patterns of both junctions. The ratio between the critical currents of the junctions at zero field is extracted from the average value of the SQUID critical current and the semi-amplitude of the SQUID oscillations, resulting in Ic,2(0)/Ic,1(0) = 5.2.
Extended Data Fig. 10 Josephson current revival in parallel field.
a–c, Differential resistance R1 of JJ1 as a function of B⊥ and B|| measured in devices 2, 6 and 7 for Idc = 0 and Iac = 5 nA. All the devices are characterized by width W1 = 80 nm and length L1 = 1.6 µm, while the width of the superconducting leads WS1 (see Fig. 1a) is varied. Device 2 is characterized by WS1 = 160 nm, device 6 has WS1 = 500 nm and device 7 WS1 = 1 µm. In the case of WS1 = 160 nm (a), JJ1 becomes resistive at B|| ≈ 1.1 T, and a supercurrent revival is observed above 2 T. The normal state transition of the epitaxial Al occurs at B|| ≈ 2.4 T, where the junction resistance reaches a value of about 1 kΩ without any magnetic-field dependence. When WS1 is increased, the supercurrent revivals occur at lower values of B|| and show an evident periodicity of about 300 mT and about 150 mT for WS1 = 500 nm (b) and WS1 = 1 µm (c), respectively. d, e, R1 as a function of Idc and B|| measured in devices 6 and 7 for B⊥ = 0, as shown by the dashed lines in b and c. The Josephson current shows a clear Fraunhofer pattern due to orbital effects of the in-plane field penetrating the proximitized 2DEG below the Al leads10. The measurements were performed with the QPC and junction 2 pinched off.
Rights and permissions
About this article
Cite this article
Fornieri, A., Whiticar, A.M., Setiawan, F. et al. Evidence of topological superconductivity in planar Josephson junctions. Nature 569, 89–92 (2019). https://doi.org/10.1038/s41586-019-1068-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1068-8
This article is cited by
-
Superconducting diode effect sign change in epitaxial Al-InAs Josephson junctions
Communications Physics (2024)
-
Superconducting tunnel junctions with layered superconductors
Quantum Frontiers (2024)
-
Aharonov–Bohm effect modified by the Majorana bound states in a parallel double-quantum-dot structure
Journal of the Korean Physical Society (2024)
-
Microwave-induced conductance replicas in hybrid Josephson junctions without Floquet—Andreev states
Nature Communications (2023)
-
Majorana zero modes in Y-shape interacting Kitaev wires
npj Quantum Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.