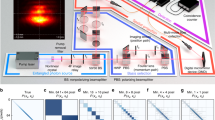
Abstract
Quantum scrambling is the dispersal of local information into many-body quantum entanglements and correlations distributed throughout an entire system. This concept accompanies the dynamics of thermalization in closed quantum systems, and has recently emerged as a powerful tool for characterizing chaos in black holes1,2,3,4. However, the direct experimental measurement of quantum scrambling is difficult, owing to the exponential complexity of ergodic many-body entangled states. One way to characterize quantum scrambling is to measure an out-of-time-ordered correlation function (OTOC); however, because scrambling leads to their decay, OTOCs do not generally discriminate between quantum scrambling and ordinary decoherence. Here we implement a quantum circuit that provides a positive test for the scrambling features of a given unitary process5,6. This approach conditionally teleports a quantum state through the circuit, providing an unambiguous test for whether scrambling has occurred, while simultaneously measuring an OTOC. We engineer quantum scrambling processes through a tunable three-qubit unitary operation as part of a seven-qubit circuit on an ion trap quantum computer. Measured teleportation fidelities are typically about 80 per cent, and enable us to experimentally bound the scrambling-induced decay of the corresponding OTOC measurement.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All relevant data are available from the corresponding author upon request.
References
Hayden, P. & Preskill, J. Black holes as mirrors: quantum information in random subsystems. J. High Energy Phys. 2007, 120 (2007).
Kitaev, A. A simple model of quantum holography. http://online.kitp.ucsb.edu/online/entangled15/kitaev/ (2015).
Shenker, S. H. & Stanford, D. Black holes and the butterfly effect. J. High Energy Phys. 2014, 67 (2014).
Maldacena, J., Shenker, S. H. & Stanford, D. A bound on chaos. J. High Energy Phys. 2016, 106 (2016).
Yoshida, B. & Kitaev, A. Efficient decoding for the Hayden-Preskill protocol. Preprint at http://arxiv.org/abs/1710.03363 (2017).
Yoshida, B. & Yao, N. Y. Disentangling scrambling and decoherence via quantum teleportation. Phys. Rev. X 9, 011006 (2018).
Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Ann. Rev. Condensed Matter Phys. 6, 15–38 (2015).
Maldacena, J. The large-N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 38, 1113 (1999).
Hawking, S. W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 14, 2460–2473 (1976).
Page, D. N. Average entropy of a subsystem. Phys. Rev. Lett. 71, 1291–1294 (1993).
Gao, P., Jafferis, D. L. & Wall, A. C. Traversable wormholes via a double trace deformation. J. High Energy Phys. 2017, 151 (2017).
Maldacena, J., Stanford, D. & Yang, Z. Diving into traversable wormholes. Fortschr. Phys. 65, 1700034 (2017).
Swingle, B., Bentsen, G., Schleier-Smith, M. & Hayden, P. Measuring the scrambling of quantum information. Phys. Rev. A 94, 040302 (2016).
Yao, N. Y. et al. Interferometric approach to probing fast scrambling. Preprint at http://arxiv.org/abs/1607.01801 (2016).
Li, J. et al. Measuring out-of-time-order correlators on a nuclear magnetic resonance quantum simulator. Phys. Rev. X 7, 031011 (2017).
Gärttner, M. et al. Measuring out-of-time-order correlations and multiple quantum spectra in a trapped-ion quantum magnet. Nature Phys. 13, 781–786 (2017).
Meier, E. J., Ang’ong’a, J., An, F. A. & Gadway, B. Exploring quantum signatures of chaos on a Floquet synthetic lattice. Preprint at http://arxiv.org/abs/1705.06714 (2017).
Wei, K. X., Ramanathan, C. & Cappellaro, P. Exploring localization in nuclear spin chains. Phys. Rev. Lett. 120, 070501 (2018).
Yunger Halpern, N., Swingle, B. & Dressel, J. Quasiprobability behind the out-of-time-ordered correlator. Phys. Rev. A 97, 042105 (2018).
Blake, M., Davison, R. A. & Sachdev, S. Thermal diffusivity and chaos in metals without quasiparticles. Phys. Rev. D 96, 106008 (2017).
Banerjee, S. & Altman, E. Solvable model for a dynamical quantum phase transition from fast to slow scrambling. Phys. Rev. B 95, 134302 (2017).
Larkin, A. I. & Ovchinnikov, Y. N. Quasiclassical method in the theory of superconductivity. Sov. Phys. JETP 28, 1200–1205 (1969).
Roberts, D. A., Stanford, D. & Susskind, L. Localized shocks. J. High Energy Phys. 2015, 51 (2015).
Swingle, B. & Yunger Halpern, N. Resilience of scrambling measurements. Phys. Rev. A 97, 062113 (2018).
Maldacena, J. & Susskind, L. Cool horizons for entangled black holes. Fortschr. Phys. 61, 781–811 (2013).
Hosur, P., Qi, X.-L., Roberts, D. A. & Yoshida, B. Chaos in quantum channels. J. High Energy Phys. 2016, 4 (2016).
Debnath, S. et al. Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63–66 (2016).
Olmschenk, S. et al. Manipulation and detection of a trapped Yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007).
Lanyon, B. P. et al. Universal digital quantum simulation with trapped ions. Science 334, 57–61 (2011).
Cirac, J. I. & Zoller, P. Goals and opportunities in quantum simulation. Nat. Phys. 8, 264–266 (2012).
Grover, L. K. in Proc. Twenty-eighth Annual ACM Symposium on Theory of Computing (STOC ’96) 212–219 (ACM, New York, 1996); https://doi.org/10.1145/237814.237866.
Maldacena, J. Eternal black holes in anti-de Sitter. J. High Energy Phys. 2003, 021 (2003).
Knill, E. et al. Randomized benchmarking of quantum gates. Phys. Rev. A 77, 012307 (2008).
Mølmer, K. & Sørensen, A. Multiparticle entanglement of hot trapped ions. Phys. Rev. Lett. 82, 1835 (1999).
Zhu, S.-L., Monroe, C. & Duan, L.-M. Arbitrary-speed quantum gates within large ion crystals through minimum control of laser beams. Europhys. Lett. 73, 485–491 (2006).
Choi, T. et al. Optimal quantum control of multimode couplings between trapped ion qubits for scalable entanglement. Phys. Rev. Lett. 112, 190502 (2014).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993).
Acknowledgements
We gratefully acknowledge discussions with R. Bousso, D. Harlow, F. Machado, I. Siddiqi, L. Susskind and Q. Zhuang. Additionally, we thank E. Edwards for the development of Fig. 1. This work is supported in part by the ARO through the IARPA LogiQ programme, the AFOSR MURI on Quantum Measurement and Verification, the ARO MURI on Modular Quantum Circuits, the DOE ASCR Program, and the NSF Physics Frontier Center at JQI. T.S. and N.Y.Y. acknowledge support from the Office of Science, Office of High Energy Physics of the US Department of Energy under contract number DE-AC02-05CH11231 through the COMPHEP pilot “Probing information scrambling via quantum teleportation” and the Office of Advanced Scientific Computing Research, Quantum Algorithm Teams Program. Research at the Perimeter Institute is supported by the Government of Canada through Innovation, Science and Economic Development Canada and by the province of Ontario through the Ministry of Economic Development, Job Creation and Trade. T.S. acknowledges support from the National Science Foundation Graduate Research Fellowship Program under grant number DGE 1752814.
Reviewer information
Nature thanks Daniel Harlow and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
K.A.L., C.F., N.M.L. and C.M. all contributed equally to the data collection and analysis presented in this manuscript. T.S. and N.Y.Y. contributed equally to the numerical simulation. All authors contributed equally in designing and planning experiments.
Corresponding author
Ethics declarations
Competing interests
The authors declare competing interests: C.M. is a founding scientist of IonQ, Inc.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Experimental apparatus.
Horizontal, dark-purple counter-propagating laser beams are illustrated with a large global beam illuminating one side of the chain and two of the seven individually modulated, tightly focused beams on the other side. The middle seven of the nine 171Yb+ ions are imaged, which allows us to address each qubit independently. Individual addressing is accomplished by imagining each ion onto an individual photomultiplier tube. The light purple, vertical light cones represent light collection from the ions onto the photomultiplier tubes.
Extended Data Fig. 2 Circuit representation of the scrambling unitary used for the probabilistic teleportation scheme.
See equation (4). The scheme consists of six two-qubit entangling XX-gates and individual Z-rotations.
Extended Data Fig. 3 Experimental sequence used for the probabilistic teleportation scheme.
Any one of the three Bell measurements can be used. The scrambling unitary has been simplified using the identity given in equation (6).
Extended Data Fig. 5 Circuit depicting experiment from Fig. 2.
a, Circuit for the unitary used in Fig. 2. b, The same unitary with varying degrees of scrambling for the data in Fig. 2. The angles of the Z-rotations are changed according to \(\theta =\pm \frac{\alpha {\rm{\pi }}}{2}\) to continuously scan between not scrambling (α = 0) and maximally scrambling (α = 1).
Extended Data Fig. 6 Circuit representation of the scrambling unitary from equation (7), used for the data in Fig. 4.
The breakdown into native gates for the experimental implementation is shown in Extended Data Fig. 7. A reduced circuit, made up of only the first three controlled-Z gates, is used to create the classical scrambling unitary \({\hat{U}}_{{\rm{c}}}\).
Extended Data Fig. 7 The scrambling unitary from equation (7) compiled into native gates.
This circuit was used for the measurements in Fig. 4.
Rights and permissions
About this article
Cite this article
Landsman, K.A., Figgatt, C., Schuster, T. et al. Verified quantum information scrambling. Nature 567, 61–65 (2019). https://doi.org/10.1038/s41586-019-0952-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-0952-6
This article is cited by
-
Quantum many-body simulations on digital quantum computers: State-of-the-art and future challenges
Nature Communications (2024)
-
Many-body Hilbert space scarring on a superconducting processor
Nature Physics (2023)
-
Many-body quantum chaos in stroboscopically-driven cold atoms
Communications Physics (2023)
-
Exploiting disorder to probe spin and energy hydrodynamics
Nature Physics (2023)
-
Charge transport, information scrambling and quantum operator-coherence in a many-body system with U(1) symmetry
Journal of High Energy Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.