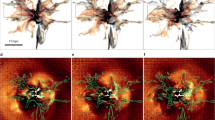
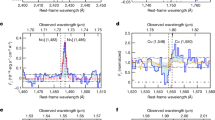
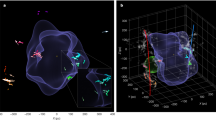
Abstract
The origin of the supermassive black holes that inhabit the centres of massive galaxies remains unclear1,2. Direct-collapse black holes—remnants of supermassive stars, with masses around 10,000 times that of the Sun—are ideal seed candidates3,4,5,6. However, their very existence and their formation environment in the early Universe are still under debate, and their supposed rarity makes modelling their formation difficult7,8. Models have shown that rapid collapse of pre-galactic gas (with a mass infall rate above some critical value) in metal-free haloes is a requirement for the formation of a protostellar core that will then form a supermassive star9,10. Here we report a radiation hydrodynamics simulation of early galaxy formation11,12 that produces metal-free haloes massive enough and with sufficiently high mass infall rates to form supermassive stars. We find that pre-galactic haloes and their associated gas clouds that are exposed to a Lyman–Werner intensity roughly three times the intensity of the background radiation and that undergo at least one period of rapid mass growth early in their evolution are ideal environments for the formation of supermassive stars. The rapid growth induces substantial dynamical heating13,14, amplifying the Lyman–Werner suppression that originates from a group of young galaxies 20 kiloparsecs away. Our results strongly indicate that the dynamics of structure formation, rather than a critical Lyman–Werner flux, is the main driver of the formation of massive black holes in the early Universe. We find that the seeds of massive black holes may be much more common than previously considered in overdense regions of the early Universe, with a co-moving number density up to 10−3 per cubic megaparsec.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The numerical experiments presented here were run with a hybrid OpenMP+MPI fork of the Enzo code, which is available from https://bitbucket.org/jwise77/openmp, using the changeset bcb436949d16. The data are publicly available from the Renaissance Simulation Laboratory at http://girder.rensimlab.xyz.
References
Volonteri, M. The formation and evolution of massive black holes. Science 337, 544–547 (2012).
Greif, T. H. The numerical frontier of the high-redshift Universe. Comput. Astrophys. Cosmol. 2, 3 (2015).
Omukai, K. Primordial star formation under far-ultraviolet radiation. Astrophys. J. 546, 635–651 (2001).
Begelman, M. C., Volonteri, M. & Rees, M. J. Formation of supermassive black holes by direct collapse in pre-galactic haloes. Mon. Not. R. Astron. Soc. 370, 289–298 (2006).
Hosokawa, T., Omukai, K. & Yorke, H. W. Rapidly accreting supergiant protostars: embryos of supermassive black holes? Astrophys. J. 756, 93 (2012).
Ardaneh, K. et al. Direct collapse to supermassive black hole seeds with radiation transfer: cosmological haloes. Mon. Not. R. Astron. Soc. 479, 2277–2293 (2018).
Habouzit, M., Volonteri, M., Latif, M., Dubois, Y. & Peirani, S. On the number density of ‘direct collapse’ black hole seeds. Mon. Not. R. Astron. Soc. 463, 529–540 (2016).
Chon, S., Hosokawa, T. & Yoshida, N. Radiation hydrodynamics simulations of the formation of direct-collapse supermassive stellar systems. Mon. Not. R. Astron. Soc. 475, 4104–4121 (2018).
Hosokawa, T., Yorke, H. W., Inayoshi, K., Omukai, K. & Yoshida, N. Formation of primordial supermassive stars by rapid mass accretion. Astrophys. J. 778, 178 (2013).
Umeda, H., Hosokawa, T., Omukai, K. & Yoshida, N. The final fates of accreting supermassive stars. Astrophys. J. 830, L34 (2016).
O’Shea, B. W., Wise, J. H., Xu, H. & Norman, M. L. Probing the ultraviolet luminosity function of the earliest galaxies with the renaissance simulations. Astrophys. J. 807, L12 (2015).
Xu, H., Wise, J. H., Norman, M. L., Ahn, K. & O’Shea, B. W. Galaxy properties and UV escape fractions during the epoch of reionization: results from the Renaissance simulations. Astrophys. J. 833, 84 (2016).
Yoshida, N., Abel, T., Hernquist, L. & Sugiyama, N. Simulations of early structure formation: primordial gas clouds. Astrophys. J. 592, 645–663 (2003).
Fernandez, R., Bryan, G. L., Haiman, Z. & Li, M. H2 suppression with shocking inflows: testing a pathway for supermassive black hole formation. Mon. Not. R. Astron. Soc. 439, 3798–3807 (2014).
Mortlock, D. J. et al. A luminous quasar at a redshift of z = 7.085. Nature 474, 616–619 (2011).
Bañados, E. et al. An 800-million-solar-mass black hole in a significantly neutral Universe at a redshift of 7.5. Nature 553, 473–476 (2018).
Bryan, G. L. et al. ENZO: an adaptive mesh refinement code for astrophysics. Astrophys. J. Suppl. Ser. 211, 19 (2014).
Wise, J. H. & Abel, T. ENZO+MORAY: radiation hydrodynamics adaptive mesh refinement simulations with adaptive ray tracing. Mon. Not. R. Astron. Soc. 414, 3458–3491 (2011).
Shang, C., Bryan, G. L. & Haiman, Z. Supermassive black hole formation by direct collapse: keeping protogalactic gas H2 free in dark matter haloes with virial temperatures T vir ≳ 104 K. Mon. Not. R. Astron. Soc. 402, 1249–1262 (2010).
Agarwal, B., Smith, B., Glover, S., Natarajan, P. & Khochfar, S. New constraints on direct collapse black hole formation in the early Universe. Mon. Not. R. Astron. Soc. 459, 4209–4217 (2016).
Glover, S. C. O. Simulating the formation of massive seed black holes in the early Universe – I. An improved chemical model. Mon. Not. R. Astron. Soc. 451, 2082–2096 (2015).
Machacek, M. E., Bryan, G. L. & Abel, T. Simulations of pregalactic structure formation with radiative feedback. Astrophys. J. 548, 509–521 (2001).
Schleicher, D. R. G., Palla, F., Ferrara, A., Galli, D. & Latif, M. Massive black hole factories: supermassive and quasi-star formation in primordial halos. Astron. Astrophys. 558, A59 (2013).
Hosokawa, T. et al. Formation of massive primordial stars: intermittent UV feedback with episodic mass accretion. Astrophys. J. 824, 119 (2016).
Sakurai, Y., Hosokawa, T., Yoshida, N. & Yorke, H. W. Formation of primordial supermassive stars by burst accretion. Mon. Not. R. Astron. Soc. 452, 755–764 (2015).
Hirano, S., Hosokawa, T., Yoshida, N. & Kuiper, R. Supersonic gas streams enhance the formation of massive black holes in the early universe. Science 357, 1375–1378 (2017).
Onoue, M. et al. Minor contribution of quasars to ionizing photon budget at z ∼ 6: update on quasar luminosity function at the faint end with Subaru/Suprime-Cam. Astrophys. J. 847, L15 (2017).
Kim, Y. et al. The Infrared Medium-deep Survey. IV. The low Eddington ratio of a faint quasar at z ∼ 6: not every supermassive black hole is growing fast in the early Universe. Astrophys. J. 855, 138 (2018).
Turk, M. J. et al. yt: a multi-code analysis toolkit for astrophysical simulation data. Astrophys. J. Suppl. Ser. 192, 9 (2011).
Abel, T., Bryan, G. L. & Norman, M. L. The formation of the first star in the Universe. Science 295, 93–98 (2002).
O’Shea, B. W. & Norman, M. L. Population III star formation in a ΛCDM Universe. I. The effect of formation redshift and environment on protostellar accretion rate. Astrophys. J. 654, 66–92 (2007).
Turk, M. J., Abel, T. & O’Shea, B. The formation of population III binaries from cosmological initial conditions. Science 325, 601–605 (2009).
Xu, H., Wise, J. H. & Norman, M. L. Population III stars and remnants in high-redshift galaxies. Astrophys. J. 773, 83 (2013).
Xu, H., Ahn, K., Wise, J. H., Norman, M. L. & O’Shea, B. W. Heating the intergalactic medium by X-Rays from population III binaries in high-redshift galaxies. Astrophys. J. 791, 110 (2014).
Chen, P., Wise, J. H., Norman, M. L., Xu, H. & O’Shea, B. W. Scaling relations for galaxies prior to reionization. Astrophys. J. 795, 144 (2014).
Ahn, K., Xu, H., Norman, M. L., Alvarez, M. A. & Wise, J. H. Spatially extended 21 cm signal from strongly clustered UV and X-ray sources in the early Universe. Astrophys. J. 802, 8 (2015).
Xu, H., Norman, M. L., O’Shea, B. W. & Wise, J. H. Late pop III star formation during the epoch of reionization: results from the Renaissance simulations. Astrophys. J. 823, 140 (2016).
Komatsu, E. et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: cosmological interpretation. Astrophys. J. Suppl. Ser. 192, 18 (2011).
Hahn, O. & Abel, T. Multi-scale initial conditions for cosmological simulations. Mon. Not. R. Astron. Soc. 415, 2101–2121 (2011).
Abel, T., Anninos, P., Zhang, Y. & Norman, M. L. Modeling primordial gas in numerical cosmology. New Astron. 2, 181–207 (1997).
Smith, B. D., Turk, M. J., Sigurdsson, S., O’Shea, B. W. & Norman, M. L. Three modes of metal-enriched star formation in the early Universe. Astrophys. J. 691, 441–451 (2009).
Behroozi, P. S., Wechsler, R. H. & Wu, H.-Y. The ROCKSTAR phase-space temporal halo finder and the velocity offsets of cluster cores. Astrophys. J. 762, 109 (2013).
Behroozi, P. S. et al. Gravitationally consistent halo catalogs and merger trees for precision cosmology. Astrophys. J. 763, 18 (2013).
Wise, J. H., Turk, M. J., Norman, M. L. & Abel, T. The birth of a galaxy: primordial metal enrichment and stellar populations. Astrophys. J. 745, 50 (2012).
Regan, J. A., Johansson, P. H. & Wise, J. H. Forming super-massive black hole seeds under the influence of a nearby anisotropic multi-frequency source. Mon. Not. R. Astron. Soc. 459, 3377–3394 (2016).
Wise, J. H. & Abel, T. Suppression of H2 cooling in the ultraviolet background. Astrophys. J. 671, 1559–1567 (2007).
O’Shea, B. W. & Norman, M. L. Population III star formation in a Λ CDM Universe. II. Effects of a photodissociating background. Astrophys. J. 673, 14–33 (2008).
Naoz, S., Yoshida, N. & Gnedin, N. Y. Simulations of early baryonic structure formation with stream velocity. II. The gas fraction. Astrophys. J. 763, 27 (2013).
Regan, J. A., Johansson, P. H. & Wise, J. H. The effect of dark matter resolution on the collapse of baryons in high-redshift numerical simulations. Mon. Not. R. Astron. Soc. 449, 3766–3779 (2015).
Kitsionas, S. & Whitworth, A. P. Smoothed particle hydrodynamics with particle splitting, applied to self-gravitating collapse. Mon. Not. R. Astron. Soc. 330, 129–136 (2002).
Bromm, V. & Loeb, A. Formation of the first supermassive black holes. Astrophys. J. 596, 34–46 (2003).
Dotti, M., Colpi, M., Haardt, F. & Mayer, L. Supermassive black hole binaries in gaseous and stellar circumnuclear discs: orbital dynamics and gas accretion. Mon. Not. R. Astron. Soc. 379, 956–962 (2007).
Hirano, S. et al. One hundred first stars: protostellar evolution and the final masses. Astrophys. J. 781, 60 (2014).
Chiaki, G. & Yoshida, N. Particle splitting in smoothed particle hydrodynamics based on Voronoi diagram. Mon. Not. R. Astron. Soc. 451, 3955–3963 (2015).
Wolcott-Green, J., Haiman, Z. & Bryan, G. L. Photodissociation of H2 in protogalaxies: modelling self-shielding in three-dimensional simulations. Mon. Not. R. Astron. Soc. 418, 838–852 (2011).
Smith, B. D. et al. GRACKLE: a chemistry and cooling library for astrophysics. Mon. Not. R. Astron. Soc. 466, 2217–2234 (2017).
Barkana, R. & Loeb, A. In the beginning: the first sources of light and the reionization of the Universe. Phys. Rep. 349, 125–238 (2001).
Wise, J. H. & Abel, T. Resolving the formation of protogalaxies. I. Virialization. Astrophys. J. 665, 899–910 (2007).
Wechsler, R. H., Bullock, J. S., Primack, J. R., Kravtsov, A. V. & Dekel, A. Concentrations of dark halos from their assembly histories. Astrophys. J. 568, 52–70 (2002).
Regan, J. A. & Haehnelt, M. G. The formation of compact massive self-gravitating discs in metal-free haloes with virial temperatures of 13000-30000K. Mon. Not. R. Astron. Soc. 393, 858–871 (2009).
Wang, B. & Silk, J. Gravitational instability and disk star formation. Astrophys. J. 427, 759–769 (1994).
Hartwig, T., Agarwal, B. & Regan, J. A. Gravitational wave signals from the first massive black hole seeds. Mon. Not. R. Astron. Soc. 479, L23–L27 (2018).
Shu, F. H. Self-similar collapse of isothermal spheres and star formation. Astrophys. J. 214, 488–497 (1977).
Bonnell, I. A., Bate, M. R. & Zinnecker, H. On the formation of massive stars. Mon. Not. R. Astron. Soc. 298, 93–102 (1998).
Hosokawa, T., Yorke, H. W. & Omukai, K. Evolution of massive protostars via disk accretion. Astrophys. J. 721, 478–492 (2010).
Woods, T. E., Heger, A., Whalen, D. J., Haemmerlé, L. & Klessen, R. S. On the maximum mass of accreting primordial supermassive stars. Astrophys. J. 842, L6 (2017).
Chen, K.-J., Heger, A., Woosley, S., Almgren, A. & Whalen, D. J. Pair instability supernovae of very massive population III stars. Astrophys. J. 792, 44 (2014).
Ota, K. et al. Large-scale environment of a z = 6.61 luminous quasar probed by Lyα emitters and Lyman break galaxies. Astrophys. J. 856, 109 (2018).
Shankar, F. The demography of supermassive black holes: growing monsters at the heart of galaxies. New Astron. Rev. 53, 57–77 (2009).
Terrazas, B. A. et al. Quiescence correlates strongly with directly measured black hole mass in central galaxies. Astrophys. J. 830, L12 (2016).
Benson, A. J. GALACTICUS: a semi-analytic model of galaxy formation. New Astron. 17, 175–197 (2012).
Heger, A., Fryer, C. L., Woosley, S. E., Langer, N. & Hartmann, D. H. How massive single stars end their life. Astrophys. J. 591, 288–300 (2003).
Chatzopoulos, E. & Wheeler, J. C. Effects of rotation on the minimum mass of primordial progenitors of pair-instability supernovae. Astrophys. J. 748, 42 (2012).
Visbal, E., Haiman, Z. & Bryan, G. L. A no-go theorem for direct collapse black holes without a strong ultraviolet background. Mon. Not. R. Astron. Soc. 442, L100–L104 (2014).
Acknowledgements
J.H.W. thanks A. Benson for assistance with the code Galacticus. J.H.W. was supported by NSF awards AST-1614333 and OAC-1835213, NASA grant NNX17AG23G, and Hubble theory grant HST-AR-14326. J.A.R. acknowledges support from the EU commission via the Marie Skłodowska-Curie Grant ‘SMARTSTARS’ (grant number 699941). B.W.O. was supported in part by NSF awards PHY-1430152, AST-1514700 and OAC-1835213, by NASA grants NNX12AC98G and NNX15AP39G, and by Hubble theory grants HST-AR-13261.01-A and HST-AR-14315.001-A. M.L.N. was supported by NSF grants AST-1109243, AST-1615858 and OAC-1835213. The simulation was performed on Blue Waters operated by the National Center for Supercomputing Applications (NCSA) with PRAC allocation support by the NSF (awards ACI-0832662, ACI-1238993 and ACI-1514580). The subsequent analysis and the re-simulations were performed with NSF’s XSEDE allocation AST-120046 on the Stampede2 resource. This research is part of the Blue Waters sustained-petascale computing project, which is supported by the NSF (awards OCI-0725070 and ACI-1238993) and the state of Illinois. Blue Waters is a joint effort of the University of Illinois at Urbana-Champaign and its NCSA. The freely available astrophysical analysis code yt29 and plotting library matplotlib were used to construct numerous plots within this paper. Computations described in this work were performed using the publicly available Enzo code, which is the product of a collaborative effort of many independent scientists from numerous institutions.
Reviewer information
Nature thanks N. Yoshida and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
J.H.W. and J.A.R. conceived the idea, performed the analysis and drafted the paper. The Renaissance simulations were conducted by H.X. and J.H.W., and the re-simulations of the target haloes were conducted by J.H.W. B.W.O. performed the Monte Carlo analysis for the number density estimate. All authors contributed to the interpretation of the results and to the text of the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Simulated and critical halo mass growth rates for SMS formation.
A halo conducive for SMS formation must grow to the atomic-cooling limit (2.2 × 107Mʘ at z = 15; orange dotted line) without hosting star formation or being chemically enriched from nearby galaxies. Haloes with masses below minimum mass Mmin,LW (dashed green line) are suppressed by an external LW radiation field. Above this mass, haloes with sufficient dynamical heating to suppress radiative cooling grow above a critical rate (equation (1)), shown for H2 number fractions fH2 of 10−4 (blue solid line), 10−5 (orange solid line) and 10−6 (green solid line). The simulated growth rates of the MMH (circles) and LWH (triangles) are above the 10−6 rate once the halo masses pass Mmin,LW. Above a halo mass of 8 × 106Mʘ (a virial temperature of 8,000 K at z = 15), dynamical heating will not suppress cooling because the atomic-radiative cooling rates are several orders of magnitude higher than the molecular ones. Both haloes grow rapidly to Mmin,LW, causing dynamical heating and preventing collapse for a sound-crossing time. The LWH grows from 8 × 106Mʘ to the atomic-cooling limit within a dynamical time of the central core. Both conditions set a critical growth rate (thick solid grey lines). All other atomic-cooling haloes (grey points) have similar growth rates between halo masses of Mmin,LW and 8 × 106Mʘ but far short of the critical growth rate. Nearly all of these haloes cool and form stars before reaching the atomic-cooling limit.
Extended Data Fig. 2 Gravitational instability of the growing core.
The ratio of the enclosed gas mass Menc and the Jeans mass MJeans as a function enclosed gas mass is shown for the MMH (solid lines) and the LWH (dashed lines) when each halo first becomes gravitationally unstable (thick black lines), that is, when Menc/MJeans ≥ 1 (shaded region), and in the final simulation state (thin blue lines). The orange circles and red squares indicate the mass scale of the collapsing gas cloud that is co-located with the centre of the host halo.
Extended Data Fig. 3 Thermal and turbulent support of the collapsing core.
a, b, Gravitational forces dominate over thermal and turbulent internal pressures within the collapsing core in the MMH (a) and the LWH (b). The thermal sound speed (blue dotted lines) and turbulent root-mean-square velocity (orange dash-dotted line) both contribute to the effective sound speed (black solid line) that provides partial resistance to a catastrophic collapse. The radial infall speed (green dashed line) shows that the flow becomes supersonic at the Jeans mass scale and then transitions to a subsonic flow at smaller mass scales. In the LWH, the radial inflow becomes transonic at a mass scale of 103Mʘ.
Extended Data Fig. 4 Rotational properties of the target haloes.
a, Radially averaged profiles of circular velocity \({v}_{{\rm{Kep}}}=\sqrt{GM/r}\) (red lines) and rotational velocity vrot (blue lines) around the largest principal axis of the MMH (dashed lines) and the LWH (solid lines) at the end of the simulation. b, Radially averaged profiles of the fractional rotational support; a ratio greater than one indicates that rotational velocities are sufficient to prevent gravitational collapse. The shaded regions show where the systems are rotationally supported: 2 × 103Mʘ–3.3 × 105Mʘ for the MMH (light shading) and 7 × 103Mʘ–6 × 104Mʘ for the LWH (dark shading). Rotation works in tandem with thermal and turbulent pressures to marginally slow the collapse, seen in the lower infall speeds at these mass scales in Extended Data Fig. 3. Inside 100Mʘ, this rotational measure becomes ill-defined because the rotation centre and centre-of-mass are not co-located; thus, we do not conclude that the inner portions are rotationally supported even though vrot/vKep > 1.
Extended Data Fig. 5 Distribution of fragmentation-prone regions.
a–d, Density-weighted projections of a local estimate of the Toomre Q parameter (equation (2)) for the MMH (a, b) and the LWH (c, d) in a field of view of 20 pc (left) and 4 pc (right), centred on the densest point and aligned to be perpendicular with the angular momentum vector of the disk. A value greater than one indicates that rotation and internal pressure stabilizes regions against fragmentation into smaller self-gravitating objects. In the MMH, this analysis highlights the clump fragments with the filaments being only marginally stable at Q ≈ 1. The sheet in the LWH that formed from a preceding major halo merger is apparent in this measure. The bulk of the sheet is only marginally stable, with the edge and collapsing centre containing an environment that is conducive to fragmentation.
Extended Data Fig. 6 Growth rates for fragmentation.
A rotating system will fragment into self-gravitating clumps only when the growth rates of the density perturbations are faster than the collapse timescale. a, Cylindrical radial profiles of Q when considering only thermal support (red) and with thermal and turbulent support (blue), for the MMH (dashed) and the LWH (solid). The shaded region indicates where the system is unstable to fragmentation. b, The unstable regions have a characteristic growth rate, defining a growth timescale tgrow, which exhibits an increasing trend with radius for the MMH (orange) and the LWH (green). c, If the ratio of tgrow and the free-fall time tff is less than one, the region can fragment before it gravitationally collapses. In the MMH, this condition is true at radii less than 0.03 pc, indicating that small-scale fragmentation might occur but will subsequently be suppressed by a rapid monolithic collapse. The LWH exhibits this feature inside 0.1 pc but is surrounded by gas that is stable against fragmentation.
Extended Data Fig. 7 Clump infall rates and timescales.
Similar to the results presented in Fig. 4d, the self-gravitating clumps are growing through radial infall. a, The infall rates are computed as the mass flux through spherical shells and steadily increase with enclosed mass. The rate in the single clump of the LWH (dotted purple line) is more than a factor three greater than the three major clumps in the MMH. The circles mark the infall rate at the clump mass. b, The infall time, the ratio of the mass enclosed and infall rate, is an informative scale that can be used to compare against star-formation timescales. This timescale is constant and approximately 10 kyr within 100Mʘ for all clumps and rises to about 100 kyr for the entire clump, marked by the circles. This rapid infall suggests that sufficient mass will collapse into the supermassive protostar before it reaches main-sequence.
Extended Data Fig. 8 Thermal and turbulent support of collapsing clumps.
a–d, Same as Extended Data Fig. 3, but for the clumps in the LWH (a) and the MMH (b–d). The vertical dotted lines mark the clump mass. The radial inflows are subsonic for all four clumps, but the clump in LWH contains transonic flows between 100Mʘ and 1,000Mʘ. Thermal support is dominant inside the clumps, unlike the larger parent Jeans-unstable system, where turbulent effective pressures are comparable to their thermal counterparts (see Extended Data Fig. 3).
Extended Data Fig. 9 Abundance estimate of DCBHs.
The cumulative probability of the co-moving number density of haloes that potentially host supermassive star formation is shown for the rare-peak (red solid line), normal (blue dashed line) and void (black dash-dotted line) regions of the Renaissance simulations. Their respective median number densities are 1.1 × 10−3, about 10−7 and 0 haloes per co-moving Mpc3. Subsequent DCBH formation is most likely to occur in overdense regions of the early Universe, whereas few or no haloes will form in average and underdense regions.
Supplementary information
Video 1
Rotation and zoom of the most massive halo (MMHalo). Projections of gas density (left) and temperature (right), zooming from cosmological scales to the supermassive star candidate
Video 2
Rotation and zoom of the most irradiated halo (LWHalo). Projections of gas density (left) and temperature (right), zooming from cosmological scales to the supermassive star candidate
Rights and permissions
About this article
Cite this article
Wise, J.H., Regan, J.A., O’Shea, B.W. et al. Formation of massive black holes in rapidly growing pre-galactic gas clouds. Nature 566, 85–88 (2019). https://doi.org/10.1038/s41586-019-0873-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-0873-4
This article is cited by
-
Evidence for heavy-seed origin of early supermassive black holes from a z ≈ 10 X-ray quasar
Nature Astronomy (2023)
-
Astrophysics with the Laser Interferometer Space Antenna
Living Reviews in Relativity (2023)
-
Turbulent cold flows gave birth to the first quasars
Nature (2022)
-
The origins of massive black holes
Nature Reviews Physics (2021)
-
Formation of the First Stars and Black Holes
Space Science Reviews (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.