Abstract
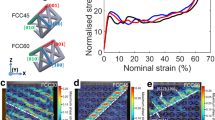
Architected materials that consist of periodic arrangements of nodes and struts are lightweight and can exhibit combinations of properties (such as negative Poisson ratios) that do not occur in conventional solids. Architected materials reported previously are usually constructed from identical ‘unit cells’ arranged so that they all have the same orientation. As a result, when loaded beyond the yield point, localized bands of high stress emerge, causing catastrophic collapse of the mechanical strength of the material. This ‘post-yielding collapse’ is analogous to the rapid decreases in stress associated with dislocation slip in metallic single crystals. Here we use the hardening mechanisms found in crystalline materials to develop architected materials that are robust and damage-tolerant, by mimicking the microscale structure of crystalline materials—such as grain boundaries, precipitates and phases. The crystal-inspired mesoscale structures in our architected materials are as important for their mechanical properties as are crystallographic microstructures in metallic alloys. Our approach combines the hardening principles of metallurgy and architected materials, enabling the design of materials with desired properties.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The datasets generated and analysed during this study are available from the corresponding author on reasonable request.
Change history
28 February 2019
In Fig. 4a of this Article, owing to an error in the production process, the scale bar inadvertently read 1 mm instead of 1 m. This error has been corrected online.
References
Cottrell, A. Dislocations and Plastic Flow in Crystals (Clarendon Press, New York, 1953).
Argon, A. Strengthening Mechanisms in Crystal Plasticity (Oxford Univ. Press, New York, 2007).
Dimiduk, D. M., Uchic, M. D. & Parthasarathy, T. A. Size-affected single-slip behavior of pure nickel microcrystals. Acta Mater. 53, 4065–4077 (2005).
Csikor, F. F., Motz, C., Weygand, D., Zaiser, M. & Zapperi, S. Dislocation avalanches, strain bursts, and the problem of plastic forming at the micrometer scale. Science 318, 251–254 (2007).
Pham, M. S., Holdsworth, S. R., Janssens, K. G. F. & Mazza, E. Cyclic deformation response of AISI 316L at room temperature: mechanical behaviour, microstructural evolution, physically-based evolutionary constitutive modelling. Int. J. Plasticity 47, 143–164 (2013).
Imrich, P. J., Kirchlechner, C., Motz, C. & Dehm, G. Differences in deformation behavior of bicrystalline Cu micropillars containing a twin boundary or a large-angle grain boundary. Acta Mater. 73, 240–250 (2014).
Hall, E. O. The deformation and ageing of mild steel: III. Discussion of Results. Proc. Phys. Soc. B 64, 747–753 (1951).
Petch, N. J. The cleavage strength of polycrystals. J. Iron Steel Inst. 174, 25–28 (1953).
Subedi, S., Beyerlein, I. J., LeSar, R. & Rollett, A. D. Strength of nanoscale metallic multilayers. Scr. Mater. 145, 132–136 (2018).
Wegst, U. G. K., Bai, H., Saiz, E., Tomsia, A. P. & Ritchie, R. O. Bioinspired structural materials. Nat. Mater. 14, 23–36 (2015).
Barthelat, F. Architectured materials in engineering and biology: fabrication, structure, mechanics and performance. Int. Mater. Rev. 60, 413–430 (2015).
Chen, P.-Y., McKittrick, J. & Meyers, M. A. Biological materials: functional adaptations and bioinspired designs. Prog. Mater. Sci. 57, 1492–1704 (2012).
Gu, G. X., Libonati, F., Wettermark, S. D. & Buehler, M. J. Printing nature: unraveling the role of nacre’s mineral bridges. J. Mech. Behav. Biomed. Mater. 76, 135–144 (2017).
Gibson, L. J. & Ashby, M. F. Cellular Solids: Structure and Properties (Cambridge Univ. Press, Cambridge, 1997).
Schaedler, T. A. & Carter, W. B. Architected cellular materials. Annu. Rev. Mater. Res. 46, 187–210 (2016).
Schaedler, T. A. et al. Ultralight metallic microlattices. Science 334, 962–965 (2011).
Lakes, R. Foam structures with a negative Poisson’s ratio. Science 235, 1038–1040 (1987).
Andreassen, E., Lazarov, B. S. & Sigmund, O. Design of manufacturable 3D extremal elastic microstructure. Mech. Mater. 69, 1–10 (2014).
Qin, Z., Jung, G. S., Kang, M. J. & Buehler, M. J. The mechanics and design of a lightweight three-dimensional graphene assembly. Sci. Adv. 3, e1601536 (2017).
Zheng, X. et al. Multiscale metallic metamaterials. Nat. Mater. 15, 1100–1106 (2016); addendum 16, 497 (2017).
Qiu, C. et al. Influence of processing conditions on strut structure and compressive properties of cellular lattice structures fabricated by selective laser melting. Mater. Sci. Eng. A 628, 188–197 (2015); corrigendum 638, 228–231 (2015).
Maskery, I. et al. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 670, 264–274 (2016).
Bouaziz, O., Brechet, Y. & Embury, J. D. Heterogeneous and architectured materials: a possible strategy for design of structural materials. Adv. Eng. Mater. 10, 24–36 (2008).
Li, L. L. et al. Microcompression and cyclic deformation behaviors of coaxial copper bicrystals with a single twin boundary. Scr. Mater. 69, 199–202 (2013).
Armstrong, R., Codd, I., Douthwaite, R. M. & Petch, N. J. The plastic deformation of polycrystalline aggregates. Philos. Mag. 7, 45–58 (1962).
Kimura, Y., Inoue, T., Yin, F. & Tsuzaki, K. Inverse temperature dependence of toughness in an ultrafine grain-structure steel. Science 320, 1057–1060 (2008).
Hirth, J. P. The influence of grain boundaries on mechanical properties. Metall. Trans. 3, 3047–3067 (1972).
Suresh, S. & Ritchie, R. O. Propagation of short fatigue cracks. Int. Mater. Rev. 29, 445–475 (1984).
Pham, M. S. & Holdsworth, S. R. Role of microstructural condition on fatigue damage development of AISI 316L at 20 and 300 °C. Int. J. Fatigue 51, 36–48 (2013).
Kobayashi, S., Nakamura, M., Tsurekawa, S. & Watanabe, T. Effect of grain boundary microstructure on fatigue crack propagation in austenitic stainless steel. J. Mater. Sci. 46, 4254–4260 (2011).
Pham, M.-S. & Holdsworth, S. Evolution of relationships between dislocation microstructures and internal stresses of AISI 316L during cyclic loading at 293 K and 573 K (20 °C and 300 °C). Metall. Mater. Trans. A 45, 738–751 (2014).
Reed, R. C. The Superalloys: Fundamentals and Applications Ch. 2 (Cambridge Univ. Press, Cambridge, 2006).
Orowan, E. Discussion on internal stresses. In Symp. Internal Stresses in Metals and Alloys 451–453 (Inst. of Metals, 1948).
Hirsch, P. B. & Humpreys, F. J. The deformation of single crystals of copper and copper-zinc alloys containing alumina particles - I. Macroscopic properties and workhardening theory. Proc. R. Soc. Lond. A 318, 45–72 (1970).
Porter, D. A. & Easterling, K. E. Phase Transformations in Metals and Alloys (CRC Press, Boca Raton, 2009).
Kresling, B. in Deployable Structures and Biological Morphology (eds Furuya, H. et al.) 188–195 (Internet-First Univ. Press, Ithaca, 2008).
Zhao, H. et al. Atomic-scale understanding of stress-induced phase transformation in cold-rolled Hf. Acta Mater. 131, 271–279 (2017).
Shan, S. et al. Multistable architected materials for trapping elastic strain energy. Adv. Mater. 27, 4296–4301 (2015).
Restrepo, D., Mankame, N. D. & Zavattieri, P. D. Phase transforming cellular materials. Extreme Mech. Lett. 4, 52–60 (2015).
Acknowledgements
M.-S.P. thanks A. Rollett, F. Dunne, C. Gourlay and S. Holdsworth for discussions, T. Walton and P. Hooper for fabricating some lattices, A. Piglione for providing an SEM image of γ/γ′ microstructure, and an Engineering Alloys Fellowship awarded by the Department of Materials, Imperial College London. M.-S.P. also thanks M. M. Attallah and D. M. Dimiduk for providing the original versions of Fig. 1b, f. I.T. is grateful for funding through EPSRC grants EP/P006566/1 and EP/L02513/1, and the Royal Academy of Engineering.
Reviewer information
Nature thanks C. Niordson, N. Pugno and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
M.-S.P. developed the idea and directed the research. C.L. carried out the computer-aided design, fabrication, mechanical tests and post analyses. J.L. performed the FEM. I.T. discussed and contributed to the development of the concept. All the authors participated in analysing and interpreting the data. The manuscript was written and approved by all authors.
Corresponding author
Ethics declarations
Competing interests
A patent developed on the basis of the approach proposed in this study has been filed, managed by Imperial Innovations.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Mimicking a crystal lattice.
a, Unit cell of the fcc lattice. b, A macro-lattice cube consisting of 8 × 8 × 8 macro-unit cells. c–e, The rotation sequence to form a twin meta-grain.
Extended Data Fig. 2 Different numbers of meta-grains within the same global volume (40 mm × 40 mm × 40 mm).
a, A single meta-grain. b, c, Two twinned meta-grains, with (b) and without (c) the outer frame. d–h, Four (d), eight (e), 16 (f), 18 (g) and 27 (h) meta-grains. The locations of the boundaries are highlighted.
Extended Data Fig. 3 Repeatability of the mechanical behaviour of architected materials.
a–c, Materials consisting of two (a), eight (b) and 16 (c) meta-grains.
Extended Data Fig. 4 Effect of meta-grain size on mechanical strength.
a, Stress–strain curves of architected materials consisting of different numbers of meta-grains. b, The flow stress σf of architected materials containing meta-grains at a given nominal strain of 40% increases as the size of the meta-grains decreases.
Extended Data Fig. 5 Mimicking crystalline grains separated by incoherent high-angle boundaries.
a, Model of eight meta-grains. b, c, The orientations of lattices (with respect to the global X, Y and Z co-ordinates) in the four meta-grains in the top (b) and bottom (c) layers.
Extended Data Fig. 6 Deformation behaviour of an architected material containing eight meta-grains separated by incoherent high-angle boundaries.
a, b, Macro-lattice fabricated from 316L stainless steel (a) and an elasto-plastic polymer (b). c, d, Stress–strain constitutive behaviour of the macro-lattices fabricated from the steel (c) and polymer (d).
Extended Data Fig. 7 Mimicking precipitates.
a, Meta-precipitate lattice (orange) embedded in the matrix. b, Cubic morphology and locations of meta-precipitates inside the fcc meta-phase. c, fcc unit cell of the matrix. d, Face-centred tetragonal unit cell of the meta-precipitate.
Extended Data Fig. 8 Repeatability of the mechanical behaviour of an architected material.
This material contains 25 meta-precipitates.
Extended Data Fig. 9 Mimicking multiple phases.
a, Single fcc-phase meta-grain. b, Single bcc-phase meta-grain. c, A cube of meta-polygrains (left panel) consisting of two meta-phases: fcc (top and bottom layers; middle panel) and bcc (middle layer; right panel).
Extended Data Fig. 10 Kresling lattice.
a, Unit cell. b, hcp-inspired meta-phase.
Extended Data Fig. 11 Helical movement changes the stack sequence of nodes.
Red lines represent the helical movements of basal nodes; for clarity, only the movement of basal nodes on the top plane are shown.
Supplementary information
Video 1
Finite-element method simulation of an architected material containing two twinned meta-grains mimicking twinned bi-crystals. Colour represents the degrees of true strain during compression
Video 2
Experimental record of the deformation behaviour of an architected hexagonal lattice during a compression loading–unloading cycle
Video 3
Finite-element method simulation of the deformation behaviour of an architected hexagonal lattice during a compression loading–unloading cycle. Colour represents the degrees of true strain during deformation
Rights and permissions
About this article
Cite this article
Pham, MS., Liu, C., Todd, I. et al. Damage-tolerant architected materials inspired by crystal microstructure. Nature 565, 305–311 (2019). https://doi.org/10.1038/s41586-018-0850-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0850-3
This article is cited by
-
Wood-inspired metamaterial catalyst for robust and high-throughput water purification
Nature Communications (2024)
-
Obtaining auxetic and isotropic metamaterials in counterintuitive design spaces: an automated optimization approach and experimental characterization
npj Computational Materials (2024)
-
Strain and Microstructural Evolution in Architected Lattices: A Comparison of Electron Beam and Laser Powder Bed Fusion
Metallurgical and Materials Transactions A (2024)
-
Metallurgy and Solidification Microstructure Control of Fusion-Based Additive Manufacturing Fabricated Metallic Alloys: A Review
Acta Metallurgica Sinica (English Letters) (2024)
-
Manufacturability-aware deep generative design of 3D metamaterial units for additive manufacturing
Structural and Multidisciplinary Optimization (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.