Abstract
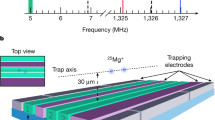
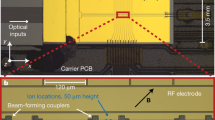
Quantum error correction is essential for realizing the full potential of large-scale quantum information processing devices1,2. Fundamental to its experimental realization is the repetitive detection of errors via projective measurements of quantum correlations among qubits, as well as corrections using conditional feedback3. Repetitive application of such tasks requires that they neither induce unwanted crosstalk nor impede further control operations, which is challenging owing to the need to dissipatively couple qubits to the classical world for detection and reinitialization. For trapped ions, state readout involves scattering large numbers of resonant photons, which increases the probability of stray light causing errors on nearby qubits and leads to undesirable recoil heating of the ion motion. Here we demonstrate up to 50 sequential measurements of correlations between two beryllium ion microwave qubits using an ancillary optical qubit in a calcium ion, and implement feedback that allows us to stabilize two-qubit subspaces as well as Bell states, a class of maximally entangled states. Multi-qubit mixed-species gates are used to transfer information within the register from the qubit to the ancilla, enabling readout with negligible crosstalk to the data qubits. Heating of the ion motion during detection is mitigated by recooling all three ions using light that interacts with only the calcium ion, known as sympathetic cooling. A key element of our experimental setup is a powerful classical control system that features flexible in-sequence processing for feedback control. The methods employed here provide essential tools for scaling trapped-ion quantum computing, quantum-state control and entanglement-enhanced quantum metrology4.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data generated and analysed during this study are available from the corresponding authors upon reasonable request.
References
Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996).
Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493–R2496 (1995).
Gottesman, D. Theory of fault-tolerant quantum computation. Phys. Rev. A 57, 127–137 (1998).
Leibfried, D. et al. Toward Heisenberg-limited spectroscopy with multiparticle entangled states. Science 304, 1476–1478 (2004).
Terhal, B. M. Quantum error correction for quantum memories. Rev. Mod. Phys. 87, 307–346 (2015).
Steane, A. M. Overhead and noise threshold of fault-tolerant quantum error correction. Phys. Rev. A 68, 042322 (2003).
Cory, D. G. et al. Experimental quantum error correction. Phys. Rev. Lett. 81, 2152–2155 (1998).
Chiaverini, J. et al. Realization of quantum error correction. Nature 432, 602–605 (2004).
Reed, M. D. et al. Realization of three-qubit quantum error correction with superconducting circuits. Nature 482, 382–385 (2012).
Barreiro, J. T. et al. An open-system quantum simulator with trapped ions. Nature 470, 486–491 (2011).
Pfaff, W. et al. Demonstration of entanglement-by-measurement of solid-state qubits. Nat. Phys. 9, 29–33 (2013).
Ristè, D. et al. Deterministic entanglement of superconducting qubits by parity measurement and feedback. Nature 502, 350–354 (2013).
Cramer, J. et al. Repeated quantum error correction on a continuously encoded qubit by real-time feedback. Nat. Commun. 7, 11526 (2016).
Sun, L. et al. Tracking photon jumps with repeated quantum non-demolition parity measurements. Nature 511, 444–448 (2014).
Monz, T. et al. Realization of a scalable Shor algorithm. Science 351, 1068–1070 (2016).
Schmidt, P. O. et al. Spectroscopy using quantum logic. Science 309, 749–752 (2005).
Tan, T. R. et al. Multi-element logic gates for trapped-ion qubits. Nature 528, 380–383 (2015).
Barrett, M. D. et al. Sympathetic cooling of 9Be+and 24Mg+for quantum logic. Phys. Rev. A 68, 042302 (2003).
Home, J. P. et al. Complete methods set for scalable ion trap quantum information processing. Science 325, 1227–1230 (2009).
Hume, D. B., Rosenband, T. & Wineland, D. J. High-fidelity adaptive qubit detection through repetitive quantum nondemolition measurements. Phys. Rev. Lett. 99, 120502 (2007).
Langer, C. et al. Long-lived qubit memory using atomic ions. Phys. Rev. Lett. 95, 060502 (2005).
Ballance, C. J. et al. Hybrid quantum logic and a test of Bell’s inequality using two different atomic isotopes. Nature 528, 384–386 (2015).
Gaebler, J. P. et al. High-fidelity universal gate set for 9Be+ ion qubits. Phys. Rev. Lett. 117, 060505 (2016).
Roos, C. F. et al. Experimental demonstration of ground state laser cooling with electromagnetically induced transparency. Phys. Rev. Lett. 85, 5547–5550 (2000).
Sørensen, A. & Mølmer, K. Entanglement and quantum computation with ions in thermal motion. Phys. Rev. A 62, 022311 (2000).
Lee, P. J. et al. Phase control of trapped ion quantum gates. J. Opt. B 7, S371–S383 (2005).
Monroe, C. et al. Resolved-sideband raman cooling of a bound atom to the 3D zero-point energy. Phys. Rev. Lett. 75, 4011–4014 (1995).
Ballance, C. J., Harty, T. P., Linke, N. M., Sepiol, M. A. & Lucas, D. M. High-fidelity quantum logic gates using trapped-ion hyperfine qubits. Phys. Rev. Lett. 117, 060504 (2016).
Brown, N. C. & Brown, K. R. Comparing Zeeman qubits to hyperfine qubits in the context of the surface code: 174Yb+ and 171Yb+. Phys. Rev. A 97, 052301 (2018).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, Cambridge, 2000).
Schäfer, V. et al. Fast quantum logic gates with trapped-ion qubits. Nature 555, 75–78 (2018).
Raussendorf, R. & Briegel, H. J. A one-way quantum computer. Phys. Rev. Lett. 86, 5188–5191 (2001).
Gottesman, D. & Chuang, I. L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 402, 390–393 (1999).
de Clercq, L. E. et al. Parallel transport quantum logic gates with trapped ions. Phys. Rev. Lett. 116, 080502 (2016).
Home, J. P. Chapter 4 – quantum science and metrology with mixed-species ion chains. Adv. Atom. Mol. Opt. Phys. 62, 231–277 (2013).
Kienzler, D. et al. Quantum harmonic oscillator state synthesis by reservoir engineering. Science 347, 53–56 (2015).
Keitch, B., Negnevitsky, V. & Zhang, W. Programmable and scalable radio-frequency pulse sequence generator for multi-qubit quantum information experiments. Preprint at http://arxiv.org/abs/1710.04282 (2017).
Ralph, T. C., Bartlett, S. D., O’Brien, J. L., Pryde, G. J. & Wiseman, H. M. Quantum nondemolition measurements for quantum information. Phys. Rev. A 73, 012113 (2006).
Acknowledgements
We thank D. Kienzler, L. de Clercq and D. Nadlinger for contributions to the apparatus, J. Alonso for discussions and M. Grau and T.-L. Nguyen for reading the manuscript. We acknowledge support from the Swiss National Science Foundation through research grant 200020_165555 and through grant 51NF40-160591 from the National Centre of Competence in Research for Quantum Science and Technology (QSIT). K.K.M. is supported by an ETH Zürich Postdoctoral Fellowship. This research is partly based on work supported by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via the US Army Research Office grant W911NF-16-1-0070. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the ODNI, IARPA or the US Government. The US Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the view of the US Army Research Office.
Reviewer information
Nature thanks B. Blinov and T. Northup for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
Experimental data were taken by V.N., M.M. and K.K.M., using an apparatus built primarily by M.M., V.N., H.-Y.L. and C.F. V.N. and K.K.M. performed the data analysis, and M.M., K.K.M. and J.P.H. performed the modelling. V.N., M.M., K.K.M. and J.P.H. wrote the manuscript, with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Ion crystal and beam configuration.
Three co-trapped ions in a single harmonic potential well are addressed by Raman beam pairs for Be+ and a 729-nm beam for Ca+. The laser frequencies (written in solid text) correspond to those applied for single-qubit operations, resonant with the qubit transition (here ωCa is the optical qubit frequency, ωBe is an optical frequency near 313 nm, ω0 is the beryllium microwave qubit frequency, and ωco,1 and ωco,2 are the laser frequencies of the co-propagating Raman beams). The faint text represents modified frequencies used to address the sidebands that are associated with the in-phase centre-of-mass (COM) mode of the three-ion crystal at 1.56 MHz, at a small detuning δ to drive the entangling MS gates. Arrows above the ions indicate the normal-mode displacement directions for this mode, as well as the ‘Egyptian’ (4.20 MHz) and the out-of-phase (4.11 MHz) axial modes.
Extended Data Fig. 2 Experimental Bell measurement correlations.
Correlations between pairs of successive \({M}_{{S}_{Z}}\) measurement operations, categorized by the feedback that took place between them. Values of 1 (0) represent perfect correlation (anti-correlation). Upward-pointing (downward-pointing) triangles show the SZ (SX) correlations where no feedback occurred; thus, for SZ the sequence is SZ−SX−SZ. Pentagons (diamonds) are data obtained with the application of CX (CZ), which nominally commutes with SZ (SX); for example, the sequence SZ−SX−CX−SZ. Squares (hexagons) are correlations between two measurements in which CZ (CX)—namely, a correction that anti-commutes with the operator of interest—took place. Circles and stars indicate data for which both CX and CZ occurred. The plots use the same raw data as Fig. 3, and uncertainties reflect projection noise; the uncertainties fluctuate noticeably owing to the varying numbers of events considered for each point, which corresponds to a subset of the full dataset.
Extended Data Fig. 3 Simulated subspace measurement correlations.
By defining P(0i) as the probability of applying a feedback operation in the ith measurement round, we plot the conditional probability of feeding back on the system twice in a row (P(0i+1| 0i)) or just once (P(0i+1| 1i)) for both the experimental data and the simulation (‘sim’). Uncertainties for P(0i+1| 0i) are much larger owing to the rarity of these events (an average of 100 events over 10,000 simulated points).
Rights and permissions
About this article
Cite this article
Negnevitsky, V., Marinelli, M., Mehta, K.K. et al. Repeated multi-qubit readout and feedback with a mixed-species trapped-ion register. Nature 563, 527–531 (2018). https://doi.org/10.1038/s41586-018-0668-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0668-z
Keywords
This article is cited by
-
Seeking a quantum advantage with trapped-ion quantum simulations of condensed-phase chemical dynamics
Nature Reviews Chemistry (2024)
-
Realization of a crosstalk-avoided quantum network node using dual-type qubits of the same ion species
Nature Communications (2024)
-
Criticality-enhanced electric field gradient sensor with single trapped ions
npj Quantum Information (2024)
-
Realizing a deep reinforcement learning agent for real-time quantum feedback
Nature Communications (2023)
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.