Abstract
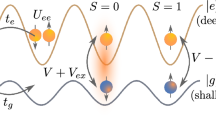
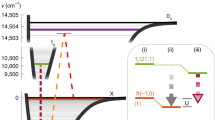
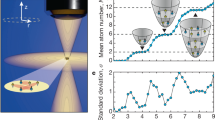
Alkaline-earth atoms have metastable ‘clock’ states with minute-long optical lifetimes, high-spin nuclei and SU(N)-symmetric interactions, making them powerful platforms for atomic clocks1, quantum information processing2 and quantum simulation3. Few-particle systems of such atoms provide opportunities to observe the emergence of complex many-body phenomena with increasing system size4. Multi-body interactions among particles are emergent phenomena, which cannot be broken down into sums over underlying pairwise interactions. They could potentially be used to create exotic states of quantum matter5,6, but have yet to be explored in ultracold fermions. Here we create arrays of isolated few-body systems in an optical clock based on a three-dimensional lattice of fermionic 87Sr atoms. We use high-resolution clock spectroscopy to directly observe the onset of elastic and inelastic multi-body interactions among atoms. We measure the frequency shifts of the clock transition for varying numbers of atoms per lattice site, from n = 1 to n = 5, and observe nonlinear interaction shifts characteristic of elastic multi-body effects. These measurements, combined with theory, elucidate an emergence of SU(N)-symmetric multi-body interactions, which are unique to fermionic alkaline-earth atoms. To study inelastic multi-body effects, we use these frequency shifts to isolate n-occupied sites in the lattice and measure the corresponding lifetimes of the clock states. This allows us to access the short-range few-body physics without experiencing the systematic effects that are encountered in a bulk gas. The lifetimes that we measure in the isolated few-body systems agree very well with numerical predictions based on a simple model for the interatomic potential, suggesting a universality in ultracold collisions. By connecting these few-body systems through tunnelling, the favourable energy and timescales of the interactions will allow our system to be used for studies of high-spin quantum magnetism7,8 and the Kondo effect3,9.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available within the paper.
References
Ludlow, A. D., Boyd, M. M., Ye, J., Peik, E. & Schmidt, P. O. Optical atomic clocks. Rev. Mod. Phys. 87, 637–701 (2015).
Daley, A. J. Quantum computing and quantum simulation with group-II atoms. Quantum Inform. Process. 10, 865–884 (2011).
Cazalilla, M. A. & Rey, A. M. Ultracold Fermi gases with emergent SU(N) symmetry. Rep. Prog. Phys. 77, 124401 (2014).
Wenz, A. N. et al. From few to many: observing the formation of a Fermi sea one atom at a time. Science 342, 457–460 (2013).
Fradkin, E. H., Nayak, C., Tsvelik, A. & Wilczek, F. A Chern-Simons effective field theory for the Pfaffian quantum Hall state. Nucl. Phys. B 516, 704–718 (1998).
Büchler, H. P., Micheli, A. & Zoller, P. Three-body interactions with cold polar molecules. Nat. Phys. 3, 726–731 (2007).
Zhang, X. et al. Spectroscopic observation of SU(N)-symmetric interactions in Sr orbital magnetism. Science 345, 1467–1473 (2014).
Gorshkov, A. V. et al. Two-orbital SU(N) magnetism with ultracold alkaline-earth atoms. Nat. Phys. 6, 289–295 (2010).
Riegger, L. et al. Localized magnetic moments with tunable spin exchange in a gas of ultracold fermions. Phys. Rev. Lett. 120, 143601 (2018).
Taie, S., Yamazaki, R., Sugawa, S. & Takahashi, Y. An SU(6) Mott insulator of an atomic Fermi gas realized by large-spin Pomeranchuk cooling. Nat. Phys. 8, 825–830 (2012).
Hofrichter, C. et al. Direct probing of the Mott crossover in the SU(N) Fermi-Hubbard model. Phys. Rev. X 6, 021030 (2016).
Scazza, F. et al. Observation of two-orbital spin-exchange interactions with ultracold SU(N)-symmetric fermions. Nat. Phys. 10, 779–784 (2014); corrigendum 11, 514 (2015).
Cappellini, G. et al. Direct observation of coherent interorbital spin-exchange dynamics. Phys. Rev. Lett. 113, 120402 (2014).
Höfer, M. et al. Observation of an orbital interaction-induced Feshbach resonance in 173Yb. Phys. Rev. Lett. 115, 265302 (2015).
Pagano, G. et al. Strongly interacting gas of two-electron fermions at an orbital Feshbach resonance. Phys. Rev. Lett. 115, 265301 (2015).
Hammer, H.-W., Nogga, A. & Schwenk, A. Colloquium: Three-body forces: from cold atoms to nuclei. Rev. Mod. Phys. 85, 197–217 (2013).
Johnson, P. R., Blume, D., Yin, X. Y., Flynn, W. F. & Tiesinga, E. Effective renormalized multi-body interactions of harmonically confined ultracold neutral bosons. New J. Phys. 14, 053037 (2012); corrigendum 20, 079501 (2018).
Will, S. et al. Time-resolved observation of coherent multi-body interactions in quantum phase revivals. Nature 465, 197–201 (2010).
Mark, M. J. et al. Precision measurements on a tunable Mott insulator of ultracold atoms. Phys. Rev. Lett. 107, 175301 (2011).
Ferlaino, F. et al. Efimov resonances in ultracold quantum gases. Few-Body Syst. 51, 113–133 (2011).
Fletcher, R. J. et al. Two- and three-body contacts in the unitary Bose gas. Science 355, 377–380 (2017).
Greene, C. H., Giannakeas, P. & Pérez-Ríos, J. Universal few-body physics and cluster formation. Rev. Mod. Phys. 89, 035006 (2017).
D’Incao, J. P. Few-body physics in resonantly interacting ultracold quantum gases. J. Phys. B 51, 043001 (2018).
Wolf, J. et al. State-to-state chemistry for three body recombination in an ultracold rubidium gas. Science 358, 921–924 (2017).
Campbell, S. L. et al. A Fermi-degenerate three-dimensional optical lattice clock. Science 358, 90–94 (2017).
Marti, G. E. et al. Imaging optical frequencies with 100µHz precision and 1.1µm resolution. Phys. Rev. Lett. 120, 103201 (2018).
Campbell, G. K. et al. Imaging the Mott insulator shells by using atomic clock shifts. Science 313, 649–652 (2006).
Kato, S. et al. Laser spectroscopic probing of coexisting superfluid and insulating states of an atomic Bose–Hubbard system. Nat. Commun. 7, 11341 (2016).
Zang, X.-P., Yang, M., Ozaydin, F., Song, W. & Cao, Z.-L. Generating multiatom entangled W states via light-matter interface based fusion mechanism. Sci. Rep. 5, 16245 (2015).
Martinez de Escobar, Y. N. et al. Two-photon photoassociative spectroscopy of ultracold 88Sr. Phys. Rev. A 78, 062708 (2008).
Burt, E. A. et al. Coherence, correlations, and collisions: what one learns about Bose-Einstein condensates from their decay. Phys. Rev. Lett. 79, 337–340 (1997).
Söding, J. et al. Three-body decay of a rubidium Bose-Einstein condensate. Appl. Phys. B 69, 257–261 (1999).
Wang, J., D’Incao, J. P., Wang, Y. & Greene, C. H. Universal three-body recombination via resonant d-wave interactions. Phys. Rev. A 86, 062511 (2012).
Acknowledgements
We acknowledge technical contributions from W. Milner, E. Oelker, J. Robinson, L. Sonderhouse and W. Zhang, and discussions with T. Bothwell, S. Bromley, C. Kennedy, D. Kedar, S. Kolkowitz, M. D. Lukin, A. Safavi-Naini and C. Sanner. This work was supported by NIST, DARPA, W911NF-16-1-0576 through ARO, AFOSR-MURI, AFOSR, NSF-1734006 and NASA. A.G. is supported by a postdoctoral fellowship from the Japan Society for the Promotion of Science and G.E.M. is supported by a postdoctoral fellowship from the National Research Council. J.P.D. acknowledges support from NSF Grant PHY-1607204.
Author information
Authors and Affiliations
Contributions
A.G., R.B.H., G.E.M., S.L.C. and J.Y. contributed to the experiments. M.A.P., P.S.J., J.P.D. and A.M.R. contributed to the development of the theoretical model. All authors discussed the results, contributed to the data analysis and worked together on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains detailed discussions of low-energy effective multi-body theory, occupation number dependence of three-body lifetime, extracting free-space scattering lengths and calculations of three-body lifetimes based on a universal van der Waals model. It also includes Supplementary Figure 1 showing trap-depth dependence of multi-body clock shifts. The calculated shifts from the three-body theory show good agreement with the experimental data in the wide range of the mean trap depths.
Rights and permissions
About this article
Cite this article
Goban, A., Hutson, R.B., Marti, G.E. et al. Emergence of multi-body interactions in a fermionic lattice clock. Nature 563, 369–373 (2018). https://doi.org/10.1038/s41586-018-0661-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0661-6
Keywords
This article is cited by
-
Reshaped three-body interactions and the observation of an Efimov state in the continuum
Nature Communications (2024)
-
Many-body correlations in one-dimensional optical lattices with alkaline-earth(-like) atoms
Scientific Reports (2023)
-
Realization of highly isolated stable few-spin systems based on alkaline-earth fermions
Frontiers of Physics (2023)
-
Heuristic machinery for thermodynamic studies of SU(N) fermions with neural networks
Nature Communications (2021)
-
Thermodynamics of a deeply degenerate SU(N)-symmetric Fermi gas
Nature Physics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.