Abstract
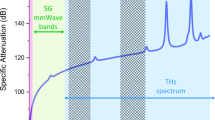
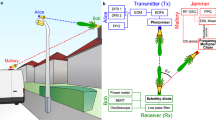
Resiliency against eavesdropping and other security threats has become one of the key design considerations for communication systems. As wireless systems become ubiquitous, there is an increasing need for security protocols at all levels, including software (such as encryption), hardware (such as trusted platform modules) and the physical layer (such as wave-front engineering)1,2,3,4,5. With the inevitable shift to higher carrier frequencies, especially in the terahertz range (above 100 gigahertz), an important consideration is the decreased angular divergence (that is, the increased directionality) of transmitted signals, owing to the reduced effects of diffraction on waves with shorter wavelengths. In recent years, research on wireless devices6,9,8 and systems9,12,11 that operate at terahertz frequencies has ramped up markedly. These high-frequency, narrow-angle broadcasts present a more challenging environment for eavesdroppers compared to the wide-area broadcasts used at lower frequencies12,13. However, despite the widespread assumption of improved security for high-frequency wireless data links14,15,16, the possibility of terahertz eavesdropping has not yet been characterized. A few recent studies have considered the issue at lower frequencies5,6,,12,13,17,18, but generally with the idea that the eavesdropper’s antenna must be located within the broadcast sector of the transmitting antenna, leading to the conclusion that eavesdropping becomes essentially impossible when the transmitted signal has sufficiently high directionality15. Here we demonstrate that, contrary to this expectation, an eavesdropper can intercept signals in line-of-sight transmissions, even when they are transmitted at high frequencies with narrow beams. The eavesdropper’s techniques are different from those for lower-frequency transmissions, as they involve placing an object in the path of the transmission to scatter radiation towards the eavesdropper. We also discuss one counter-measure for this eavesdropping technique, which involves characterizing the backscatter of the channel. We show that this counter-measure can be used to detect some, although not all, eavesdroppers. Our work highlights the importance of physical-layer security in terahertz wireless networks and the need for transceiver designs that incorporate new counter-measures.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
References
Shiu, Y.-S., Chang, S. Y., Wu, H.-C., Huang, S. C.-H. & Chen, H.-H. Physical layer security in wireless networks: a tutorial. IEEE Wirel. Commun. 18, 66–74 (2011).
Yang, N. et al. Safeguarding 5G wireless communication networks using physical layer security. IEEE Commun. Mag. 53, 20–27 (2015).
Zou, Y., Zhu, J., Wang, X. & Hanzo, L. A survey on wireless security: technical challenges, recent advances, and future trends. Proc. IEEE 104, 1727–1765 (2016).
Sun, L. & Du, Q. Physical layer security with its application in 5G networks: a review. China Commun. 14, 1–14 (2017).
Ju, Y., Wang, H.-M., Zheng, T.-X., Yin, Q. & Lee, M. H. Safeguarding millimeter wave communications against randomly located eavesdroppers. IEEE Trans. Wirel. Commun. 17, 2675–2689 (2018).
Gao, W. et al. High-contrast terahertz wave modulation by gated graphene enhanced by extraordinary transmission through ring apertures. Nano Lett. 14, 1242–1248 (2014).
Karl, N. J., McKinney, R. W., Monnai, Y., Mendis, R. & Mittleman, D. M. Frequency-division multiplexing in the terahertz range using a leaky-wave antenna. Nat. Photon. 9, 717–720 (2015).
Reichel, K. S., Mendis, R. & Mittleman, D. M. A broadband terahertz waveguide T-junction variable power splitter. Sci. Rep. 6, 28925 (2016).
Hermelo, M. F., Shih, P.-T. B., Steeg, M., Ng’oma, A. & Stöhr, A. Spectral efficient 64-QAM-OFDM terahertz communication link. Opt. Express 25, 19360–19370 (2017).
Ma, J., Karl, N. J., Bretin, S., Ducournau, G. & Mittleman, D. M. Frequency-division multiplexer and demultiplexer for terahertz wireless links. Nat. Commun. 8, 729 (2017).
Ma, J., Shrestha, R., Moeller, L. & Mittleman, D. M. Channel performance of indoor and outdoor terahertz wireless links. APL Photon. 3, 051601 (2018).
Steinmetzer, D., Chen, J., Classen, J., Knightly, E. & Hollick, M. Eavesdropping with periscopes: experimental security analysis of highly directional millimeter waves. In Proc. IEEE Conf. Commun. Netw. Security (CNS) 335–343 (IEEE, 2015).
Zhu, Y., Wang, L., Wong, K.-K. & Heath, R. W. Secure communications in millimeter wave ad hoc networks. IEEE Trans. Wirel. Commun. 16, 3205–3217 (2017).
Federici, J. & Moeller, L. Review of terahertz and subterahertz wireless communications. J. Appl. Phys. 107, 111101 (2010).
Akyildiz, I. F., Jornet, J. M. & Han, C. Terahertz band: next frontier for wireless communications. Phys. Commun. 12, 16–32 (2014).
Kürner, T. & Priebe, S. Towards THz communications – status in research, standardization and regulation. J. Infrared Millim. THz Waves 35, 53–62 (2014).
Vuppala, S., Biswas, S. & Ratnarajah, T. An analysis on secure communications in millimeter/micro-wave hybrid networks. IEEE Trans. Commun. 64, 3507–3519 (2016).
Kim, M., Hwang, E. & Kim, J.-N. Analysis of eavesdropping attack in mmWave-based WPANs with directional antennas. Wirel. Netw. 23, 355–369 (2017).
Pierpoint, M. & Rebeiz, G. M. Paving the way for 5G realization and mmWave communication systems. Mirowave J. 59, 106–108 (2016).
Xu, J. et al. Statistical analysis of path losses for sectorized wireless networks. IEEE Trans. Commun. 65, 1828–1838 (2017).
Babakhani, A., Rutledge, D. B. & Hajimiri, A. Transmitter architectures based on near-field direct antenna modulation. IEEE J. Solid-State Circuits 43, 2674–2692 (2008).
Djordjevic, I. B. Multidimensional OAM-based secure high-speed wireless communications. IEEE Access 5, 16416–16428 (2017).
Rifà-Pous, H. & Herrera-Joancomarti, J. Computational and energy costs of cryptographic algorithms on handheld devices. Future Internet 3, 31–48 (2011).
Headland, D., Monnai, Y., Abbott, D., Fumeaux, C. & Withayachumnankul, W. Tutorial: terahertz beamforming, from concept to realizations. APL Photon. 3, 051101 (2018).
Song, H.-J. & Nagatsuma, T. Present and future of terahertz communications. IEEE Trans. THz Sci. Technol. 1, 256–263 (2011).
Koenig, S. et al. Wireless sub-THz communication system with high data rate. Nat. Photon. 7, 977–981 (2013).
Ducournau, G. et al. Ultrawide-bandwidth single-channel 0.4-THz wireless link combining broadband quasi-optic photomixer and coherent detection. IEEE Trans. THz Sci. Technol. 4, 328–337 (2014).
Barros, J. & Rodrigues, M. R. D. Secrecy capacity of wireless channels. In Proc. IEEE Symp. Inform. Theory 356–360 (IEEE, 2006).
Csiszár, I. & Körner, J. Broadcast channels with confidential messages. IEEE Trans. Inf. Theory 24, 339–348 (1978).
Petrov, V., Komarov, M., Moltchanov, D., Jornet, J. M. & Koucheryavy, Y. Interference and SINR in millimeter wave and terahertz communication systems with blocking and directional antennas. IEEE Trans. Wirel. Commun. 16, 1791–1808 (2017).
Ma, J., Moeller, L. & Federici, J. F. Experimental comparison of terahertz and infrared signaling in controlled atmospheric turbulence. J. Infrared Millimeter THz Waves 36, 130–143 (2015).
Kouyoumjian, R. G. & Pathak, P. H. A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface. Proc. IEEE 62, 1448–1461 (1974).
Dorney, T. D., Symes, W. W., Baraniuk, R. G. & Mittleman, D. M. Terahertz multistatic reflection imaging. J. Opt. Soc. Am. A 19, 1432–1442 (2002).
Chen, Z. et al. 220 GHz outdoor wireless communication system based on a Schottky diode transceiver. IEICE Electron. Express 13, 1–9 (2016).
Yeh, C.-Y. & Knightly, E. W. Feasibility of passive eavesdropping in massive MIMO: an experimental approach. In Proc. IEEE Conf. Commun. Netw. Security (CNS) 1–9 (IEEE, 2018).
McNamara, D. A., Pistorius, C. W. I. & Malherbe, J. A. G. Introduction to the Uniform Geometrical Theory of Diffraction (Artech House, Boston, 1990).
Ung, B. S.-Y. et al. Low-cost ultra-thin broadband terahertz beam-splitter. Opt. Express 20, 4968–4978 (2012).
Acknowledgements
This work was funded in part by the US National Science Foundation, the US Army Research Office and the W. M. Keck Foundation.
Reviewer information
Nature thanks K.-Y. Lam and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
D.M.M. and E.K. conceived the experiments. J.M., R.S. and J.A. performed the measurements. Z.H. and J.M.J. performed the computations shown as dotted lines in Fig. 3. D.M.M., E.K. and C.-Y.Y. analysed and interpreted the data. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Rights and permissions
About this article
Cite this article
Ma, J., Shrestha, R., Adelberg, J. et al. Security and eavesdropping in terahertz wireless links. Nature 563, 89–93 (2018). https://doi.org/10.1038/s41586-018-0609-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0609-x
Keywords
This article is cited by
-
Wireless communications sensing and security above 100 GHz
Nature Communications (2023)
-
Terahertz waveform synthesis in integrated thin-film lithium niobate platform
Nature Communications (2023)
-
Propagation of THz radiation in air over a broad range of atmospheric temperature and humidity conditions
Scientific Reports (2023)
-
High-resolution terahertz digital holography based on frequency-domain diagonal extension imaging
Optical and Quantum Electronics (2023)
-
Study on detection of the internal quality of pumpkin seeds based on terahertz imaging technology
Journal of Food Measurement and Characterization (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.