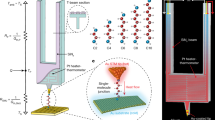
Abstract
Since the discovery a century ago1,2,3 of electronic thermal noise and shot noise, these forms of fundamental noise have had an enormous impact on science and technology research and applications. They can be used to probe quantum effects and thermodynamic quantities4,5,6,7,8,9,10,11, but they are also regarded as undesirable in electronic devices because they obscure the target signal. Electronic thermal noise is generated at equilibrium at finite (non-zero) temperature, whereas electronic shot noise is a non-equilibrium current noise that is generated by partial transmission and reflection (partition) of the incoming electrons8. Until now, shot noise has been stimulated by a voltage, either applied directly8 or activated by radiation12,13. Here we report measurements of a fundamental electronic noise that is generated by temperature differences across nanoscale conductors, which we term ‘delta-T noise’. We experimentally demonstrate this noise in atomic and molecular junctions, and analyse it theoretically using the Landauer formalism8,14. Our findings show that delta-T noise is distinct from thermal noise and voltage-activated shot noise8. Like thermal noise, it has a purely thermal origin, but delta-T noise is generated only out of equilibrium. Delta-T noise and standard shot noise have the same partition origin, but are activated by different stimuli. We infer that delta-T noise in combination with thermal noise can be used to detect temperature differences across nanoscale conductors without the need to fabricate sophisticated local probes. Thus it can greatly facilitate the study of heat transport at the nanoscale. In the context of modern electronics, temperature differences are often generated unintentionally across electronic components. Taking into account the contribution of delta-T noise in these cases is likely to be essential for the design of efficient nanoscale electronics at the quantum limit.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The datasets generated and analysed during this study are available from the corresponding author on reasonable request.
References
Schottky, W. Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern. Ann. Phys. 362, 541–567 (1918).
Johnson, J. B. Thermal agitation of electricity in conductors. Nature 119, 50–51 (1927).
Nyquist, H. Thermal agitation of electric charge in conductors. Phys. Rev. 32, 110–113 (1928).
White, D. R. et al. The status of Johnson noise thermometry. Metrologia 33, 325–335 (1996).
Saminadayar, L., Glattli, D. C., Jin, Y. & Etienne, B. Observation of the e/3 fractionally charged Laughlin quasiparticle. Phys. Rev. Lett. 79, 2526 (1997).
de Picciotto, R. et al. Direct observation of a fractional charge. Nature 389, 162–164 (1997).
van den Brom, H. E. & van Ruitenbeek, J. M. Quantum suppression of shot noise in atom-size metallic contacts. Phys. Rev. Lett. 82, 1526–1529 (1999).
Blanter, Y. M. & Büttiker, M. Shot noise in mesoscopic conductors. Phys. Rep. 336, 1–66 (2000).
Roche, P. et al. Fano factor reduction on the 0.7 conductance structure of a ballistic one-dimensional wire. Phys. Rev. Lett. 93, 116602 (2004).
Delattre, T. et al. Noisy Kondo impurities. Nat. Phys. 5, 208–212 (2009).
Jezouin, S. et al. Controlling charge quantization with quantum fluctuations. Nature 536, 58–62 (2016).
Schoelkopf, R. J., Kozhevnikov, A. A., Prober, D. E. & Rooks, M. J. Observation of ‘photon-assisted’ shot noise in a phase-coherent conductor. Phys. Rev. Lett. 80, 2437 (1998).
Reydellet, L.-H., Roche, P., Glattli, D. C., Etienne, B. & Jin, Y. Quantum partition noise of photon-created electron-hole pairs. Phys. Rev. Lett. 90, 176803 (2003).
Büttiker, M., Imry, Y., Landauer, R. & Pinhas, S. Generalized many-channel conductance formula with application to small rings. Phys. Rev. B 31, 6207 (1985).
Giazotto, F., Heikkilä, T. T., Luukanen, A., Savin, A. M. & Pekola, J. P. Opportunities for mesoscopics in thermometry and refrigeration: physics and applications. Rev. Mod. Phys. 78, 217 (2006).
Djukic, D. & van Ruitenbeek, J. M. Shot noise measurements on a single molecule. Nano Lett. 6, 789–793 (2006).
Tal, O., Krieger, M., Leerink, B. & van Ruitenbeek, J. M. Electron-vibration interaction in single-molecule junctions: from contact to tunneling regimes. Phys. Rev. Lett. 100, 196804 (2008).
Chen, R., Matt, M., Pauly, F., Cuevas, J. C. & Natelson, D. Shot noise variation within ensembles of gold atomic break junctions at room temperature. J. Phys. Condens. Matter 26, 474204 (2014).
Burtzlaff, A., Weismann, A., Brandbyge, M. & Berndt, R. Shot noise as a probe of spin-polarized transport through single atoms. Phys. Rev. Lett. 114, 016602 (2015).
Vardimon, R., Klionsky, M. & Tal, O. Indication of complete spin filtering in atomic-scale nickel oxide. Nano Lett. 15, 3894–3898 (2015).
Karimi, M. A. et al. Shot noise of 1, 4-benzenedithiol single-molecule junctions. Nano Lett. 16, 1803–1807 (2016).
Sukhorukov, E. V. & Loss, D. Noise in multiterminal diffusive conductors: Universality, nonlocality, and exchange effects. Phys. Rev. B 59, 13054 (1999).
Csonka, S., Halbritter, A. & Mihály, G. Pulling gold nanowires with a hydrogen clamp: strong interactions of hydrogen molecules with gold nanojunctions. Phys. Rev. B 73, 075405 (2006).
Nakazumi, T., Kaneko, S. & Kiguchi, M. Electron transport properties of Au, Ag, and Cu atomic contacts in a hydrogen environment. J. Phys. Chem. C 118, 7489–7493 (2014).
Muller, C. J., van Ruitenbeek, J. M. & De Jongh, L. J. Experimental observation of the transition from weak link to tunnel junction. Physica C 191, 485–504 (1992).
Reddy, P., Jang, S. Y., Segalman, R. A. & Majumdar, A. Thermoelectricity in molecular junctions. Science 315, 1568–1571 (2007).
Ludoph, B., Devoret, M. H., Esteve, D., Urbina, C. & Van Ruitenbeek, J. M. Evidence for saturation of channel transmission from conductance fluctuations in atomic-size point contacts. Phys. Rev. Lett. 82, 1530 (1999).
Rubio-Bollinger, G. et al. Single-channel transmission in gold one-atom contacts and chains. Phys. Rev. B 67, 121407 (2003).
Vardimon, R., Matt, M., Nielaba, P., Cuevas, J. C. & Tal, O. Orbital origin of the electrical conduction in ferromagnetic atomic-size contacts: insights from shot noise measurements and theoretical simulations. Phys. Rev. B 93, 085439 (2016).
Evangeli, C. et al. Engineering the thermopower of C60 molecular junctions. Nano Lett. 13, 2141–2145 (2013).
Ludoph, B. & Van Ruitenbeek, J. M. Thermopower of atomic-size metallic contacts. Phys. Rev. B 59, 12290 (1999).
Vardimon, R., Klionsky, M. & Tal, O. Experimental determination of conduction channels in atomic-scale conductors based on shot noise measurements. Phys. Rev. B 88, 161404 (2013).
Acknowledgements
O.T. appreciates the support of the Harold Perlman family, and acknowledges funding by a research grant from Dana and Yossie Hollander, the Israel Science Foundation (grant number 1089/15), and the Minerva Foundation (grant number 120865). D.S. acknowledges support from an NSERC Discovery Grant and the Canada Research Chair programme. The research of A.N. is supported by the US National Science Foundation (grant number CHE1665291), the Israel-US Binational Science Foundation, the German Research Foundation (DFG TH 820/11-1) and the University of Pennsylvania. L.S. acknowledges the Special Opportunity Graduate Travel Fellowship from the Department of Chemistry, University of Toronto.
Reviewer information
Nature thanks E. Scheer and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
The project was conceived by O.T. The experiments were designed by O.S.L. and O.T., and performed by O.S.L., under the supervision of O.T. The theoretical derivation was performed by L.S., A.N. and D.S. The manuscript was written by O.S.L., D.S. and O.T. All authors contributed to the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Characterization of Au/H2 molecular junctions.
Conductance histograms of bare Au atomic junctions (brown) and Au/H2 molecular junctions (blue) are shown. The histograms are composed from at least 1,500 conductance versus electrode displacement traces recorded at a bias voltage of 100 mV. a.u., arbitrary units.
Extended Data Fig. 2 Electronic measurement setup.
Schematic presentation of the electronic circuit for conductance and noise measurements is shown. The electronic circuit consists of two switchable measurement circuits: a conductance circuit (purple) and a noise circuit (blue).
Extended Data Fig. 3 Thermometer calibration based on thermal noise.
The temperature measured by thermal noise is shown versus that measured using the diode thermometer (black circles; the vertical error bars are smaller than the circles’ diameter). The error bars correspond to the systematic errors in our measurements. To guide the eye, the dashed grey line corresponds to a ratio of 1:1. The red line is a linear fit of the data. The calibration of the thermometers temperature is done by this fit TTN = (1.28 ± 0.02)Ttherm− 1.0 ± 0.5 K, where Ttherm is the temperature measured by the thermometer. The inset shows an example for measured thermal noise versus conductance (black dots) at a thermal noise temperature of 37.10 ± 0.04 K. The blue line is a linear fit from which the thermal noise temperature is determined. This measurement procedure is repeated at different temperatures to construct the main graph. When the junction is heated above the setup base temperature, the thermometers attached to the electrode tips always indicate lower temperatures than those determined by the thermal noise.
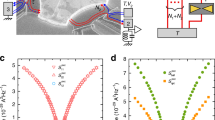
Extended Data Fig. 4 Shot noise analysis for Au/H2 junctions.
The Fano factor extracted from shot noise and conductance measurements20,29 is shown versus the conductance for different junction realizations at 4.6 K (ΔT = 0). The thick red curve provides the minimal Fano factor. Data that accumulate on this line below 1G0 indicate junctions with a single transmission channel22. The dashed line provides the maximal Fano factor that two channels can generate for the relevant conductance. The insets show transmission probabilities of the main six transmission channels based on numerical analysis of the measured Fano factor and conductance32 for the three marked cases (I, II, III) in the main panel. The error bars provide the range of transmission solutions that satisfies the measured conductance and shot noise. Inset I shows that a junction that is characterized by Fano factor and conductance data near the red curve conducts via a single dominant channel with only minor contribution from a secondary channel. In contrast, inset III exemplifies that a junction with Fano factor and conductance data near the dashed curve can conduct via two dominant channels with possible minor contributions from other channels.
Extended Data Fig. 5 Noise measurements at finite temperature differences.
a, Current–voltage curves for a set of different junction realizations at \(\bar{T}\) = 13.3 ± 0.3 K and ∆T = 12.6 ± 0.2 K. The conductance of each junction is obtained by the slope of the curve. Here, G = 0.82G0, 1.52G0, 2.57G0, 4.05G0, 5.30G0 and 6.34G0, with all values ±0.01G0, starting from the smallest slope. b, Total noise as a function of frequency for the same junctions examined in a. The top spectrum corresponds to the junction with the highest conductance. The noise is suppressed by low-pass RC filtering owing to the capacitance of the setup and the finite sample and wire resistance. c, Examples for RC transfer function and \({S}_{I}^{{\rm{i}}{\rm{n}}}\) fitting to spectra of total noise versus frequency measured at a fixed temperature of 5.4 ± 0.5 K, and different conductance values (0.51G0–6.03G0 ± 0.01G0). The arrow points in the direction of increasing conductance G. d, Same as c at a fixed conductance of G = 0.77G0 ± 0.01G0, and different temperatures (5.4 ± 0.5 K to 37.5 ± 0.9 K). The arrow points in the direction of increasing temperature T. The setup capacitance and \({S}_{I}^{{\rm{i}}{\rm{n}}}\) are extracted from the fitting. e, The data presented in b corrected by an RC transfer function followed by subtraction of \({S}_{I}^{{\rm{i}}{\rm{n}}}\). f, Total noise as a function of conductance obtained by averaging the noise presented in e in a frequency range of 180–230 kHz, coloured blue in e.
Extended Data Fig. 6 Total thermoelectric voltage and its estimated contribution to the excess noise.
a, Measured total thermoelectric voltage for the examined junctions as a function of conductance at \(\bar{T}\) = 26.3 ± 0.7 K and ∆T = 25.3 ± 0.6 K. Measurements were performed according to the method described in ref. 30. Here, we are interested in the total thermoelectric voltage that is built across the junction, since it can be a source for shot noise. b, Calculated shot noise (red curve) that is expected for the maximal measured thermovoltage in a (155 µV, marked as a red star in a), and the measured excess noise (dark circles) at the same \(\bar{T}\) and ∆T for which the thermoelectric voltage was measured. Calculated delta-T noise is given by the black curve for a single transmission channel, and by the dashed curve for two channels with equal transmission probabilities (non-approximated numerical calculations based on equation (S2) in Supplementary Information).
Extended Data Fig. 7 Excess noise measured at zero and finite temperature difference with error bars.
a, b, Excess noise as a function of conductance measured in the examined molecular junctions as presented in Fig. 2a, b, including error bars, corresponding to the systematic errors in our measurements. The size of the error bars is comparable or slightly larger than the diameter of the semitransparent red symbols.
Extended Data Fig. 8 Excess noise measured at zero and finite temperature difference for bare gold atomic junctions.
a, b, Excess noise (obtained by subtracting the average thermal noise from the total measured noise) as a function of conductance measured in bare gold atomic junctions at different temperatures at thermal equilibrium (ΔT = 0). c, d, Excess noise as a function of conductance measured at different average temperatures and finite temperature differences across the junctions (ΔT ≠ 0). Calculated delta-T noise is given by the black curve for single transmission channel probabilities (non-approximated numerical calculations based on equation (S2) in Supplementary Information). When a temperature difference is applied across the junctions, some enhancement of the excess noise is observed. The measured excess noise can be described by the theoretical expression for the delta-T noise, although the agreement is less clear than for hydrogen-based molecular junctions (Fig. 2), owing to the lack of data below 0.75G0. The spread in the results is a natural outcome of additional transmission channels that open as the conductance increases. The error bars correspond to the systematic errors in our measurements.
Extended Data Fig. 9 Fano factor obtained from noise measurements at a finite temperature difference.
The Fano factor (semitransparent black symbols) is extracted from the excess noise data presented in Fig. 2d, and the associated measured conductance using equation (2). The short-dashed horizontal line marks the zero Fano factor as a baseline. The thick blue curve provides the theoretically predicted minimal Fano factor. Data that accumulate on this line below 1G0 indicate junctions with a single transmission channel22. The long-dashed sloped line marks the maximal Fano factor that two channels can generate for the relevant conductance.
Supplementary information
Supplementary Information
This file contains the derivation of the theoretical expression for the delta-T noise, as well as more general results for the current noise under both applied voltage and temperature difference. The file further includes Supplementary Figures 1 and 2 and additional references.
Rights and permissions
About this article
Cite this article
Lumbroso, O.S., Simine, L., Nitzan, A. et al. Electronic noise due to temperature differences in atomic-scale junctions. Nature 562, 240–244 (2018). https://doi.org/10.1038/s41586-018-0592-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0592-2
Keywords
This article is cited by
-
Quasiparticle Andreev scattering in the ν = 1/3 fractional quantum Hall regime
Nature Communications (2023)
-
Low-Temperature Thermally Induced Noise in the Presence of an AC Voltage Bias
Journal of Low Temperature Physics (2023)
-
An experimental set-up to probe the quantum transport through a single atomic\(/\)molecular junction at room temperature
Pramana (2022)
-
Electronic noise generated by a temperature gradient across a hybrid normal metal–superconductor nanojunction
Applied Nanoscience (2020)
-
Thermal conductance of single-molecule junctions
Nature (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.