Abstract
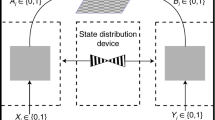
Randomness is important for many information processing applications, including numerical modelling and cryptography1,2. Device-independent quantum random-number generation (DIQRNG)3,4 based on the loophole-free violation of a Bell inequality produces genuine, unpredictable randomness without requiring any assumptions about the inner workings of the devices, and is therefore an ultimate goal in the field of quantum information science5,6,7. Previously reported experimental demonstrations of DIQRNG8,9 were not provably secure against the most general adversaries or did not close the ‘locality’ loophole of the Bell test. Here we present DIQRNG that is secure against quantum and classical adversaries10,11,12. We use state-of-the-art quantum optical technology to create, modulate and detect entangled photon pairs, achieving an efficiency of more than 78 per cent from creation to detection at a distance of about 200 metres that greatly exceeds the threshold for closing the ‘detection’ loophole of the Bell test. By independently and randomly choosing the base settings for measuring the entangled photon pairs and by ensuring space-like separation between the measurement events, we also satisfy the no-signalling condition and close the ‘locality’ loophole of the Bell test, thus enabling the realization of the loophole-free violation of a Bell inequality. This, along with a high-voltage, high-repetition-rate Pockels cell modulation set-up, allows us to accumulate sufficient data in the experimental time to extract genuine quantum randomness that is secure against the most general adversaries. By applying a large (137.90 gigabits × 62.469 megabits) Toeplitz-matrix hashing technique, we obtain 6.2469 × 107 quantum-certified random bits in 96 hours with a total failure probability (of producing a random number that is not guaranteed to be perfectly secure) of less than 10−5. Our demonstration is a crucial step towards transforming DIQRNG from a concept to a key aspect of practical applications that require high levels of security and thus genuine randomness7. Our work may also help to improve our understanding of the origin of randomness from a fundamental perspective.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request. Source Data for Fig. 3 is provided with the online version of the paper.
References
Shannon, C. E. Communication theory of secrecy systems. Bell Labs Tech. J. 28, 656–715 (1949).
Metropolis, N. & Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 44, 335–341 (1949).
Colbeck, R. Quantum and Relativistic Protocols for Secure Multi-party Computation. PhD thesis, Cambridge Univ. (2009).
Mayers, D. & Yao, A. Quantum cryptography with imperfect apparatus. In Proc. 39th Annual Symposium on Foundations of Computer Science (ed. Motwani, R.) 503–509 (IEEE, 1998).
Ma, X., Yuan, X., Cao, Z., Qi, B. & Zhang, Z. Quantum random number generation. npj Quantum Inf. 2, 16021 (2016).
Herrero-Collantes, M. & Garcia-Escartin, J. C. Quantum random number generators. Rev. Mod. Phys. 89, 015004 (2017).
Acín, A. & Masanes, L. Certified randomness in quantum physics. Nature 540, 213–219 (2016).
Pironio, S. et al. Random numbers certified by Bell’s theorem. Nature 464, 1021–1024 (2010).
Bierhorst, P. et al. Experimentally generated randomness certified by the impossibility of superluminal signals. Nature 556, 223–226 (2018).
Miller, C. A. & Shi, Y. Universal security for randomness expansion from the spot-checking protocol. SIAM J. Comput. 46, 1304–1335 (2017).
Vazirani, U. V. & Vidick, T. Certifiable quantum dice - or, testable exponential randomness expansion. Preprint at https://arxiv.org/abs/1111.6054 (2011).
Arnon-Friedman, R., Renner, R. & Vidick, T. Simple and tight device-independent security proofs. Preprint at https://arxiv.org/abs/1607.01797 (2016).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Shalm, L. K. et al. Strong loophole-free test of local realism. Phys. Rev. Lett. 115, 250402 (2015).
Giustina, M. et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 115, 250401 (2015).
Rosenfeld, W. et al. Event-ready Bell test using entangled atoms simultaneously closing detection and locality loopholes. Phys. Rev. Lett. 119, 010402 (2017).
Vazirani, U. & Vidick, T. Fully device-independent quantum key distribution. Phys. Rev. Lett. 113, 140501 (2014).
Miller, C. A. & Shi, Y. Robust protocols for securely expanding randomness and distributing keys using untrusted quantum devices. J. ACM 63, 33 (2016).
Chung, K.-M., Shi, Y. & Wu, X. Physical randomness extractors: generating random numbers with minimal assumptions. Preprint at https://arxiv.org/abs/1402.4797 (2014).
Coudron, M. & Yuen, H. Infinite randomness expansion with a constant number of devices. In Proc. 46th Annual ACM Symposium on Theory of Computing (ed. Shmoys, D.) 427–436 (ACM, 2014).
Dupuis, F., Fawzi, O. & Renner, R. Entropy accumulation. Preprint at https://arxiv.org/abs/1607.01796 (2016).
Liu, Y. et al. High-speed device-independent quantum random number generation without a detection loophole. Phys. Rev. Lett. 120, 010503 (2018).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Coudron, M., Vidick, T. & Yuen, H. Robust randomness amplifiers: upper and lower bounds. In Proc. APPROX 2013: Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques (eds Raghavendra, P. et al.) 468–483 (Springer, 2013).
Barrett, J., Colbeck, R. & Kent, A. Memory attacks on device-independent quantum cryptography. Phys. Rev. Lett. 110, 010503 (2013).
Pereira, M. D. C. et al. Demonstrating highly symmetric single-mode, single-photon heralding efficiency in spontaneous parametric downconversion. Opt. Lett. 38, 1609–1611 (2013).
Eberhard, P. H. Background level and counter efficiencies required for a loophole-free Einstein-Podolsky-Rosen experiment. Phys. Rev. A 47, R747–R750 (1993).
Zhang, Y., Glancy, S. & Knill, E. Asymptotically optimal data analysis for rejecting local realism. Phys. Rev. A 84, 062118 (2011).
Kessler, M. & Arnon-Friedman, R. Device-independent randomness amplification and privatization. Preprint at https://arxiv.org/abs/1705.04148 (2017).
Bennink, R. Optimal collinear Gaussian beams for spontaneous parametric down-conversion. Phys. Rev. A 81, 053805 (2010).
Dixon, P. B. et al. Heralding efficiency and correlated-mode coupling of near-IR fiber-coupled photon pairs. Phys. Rev. A 90, 043804 (2014).
Zhang, W. et al. NbN superconducting nanowire single photon detector with efficiency over 90% at 1550 nm wavelength operational at compact cryocooler temperature. Sci. China Phys. Mechan. Astron. 60, 120314 (2017).
Acknowledgements
We thank S.-R. Zhao, Y.-H. Li, L.-K. Chen and R. Jin for experimental assistance, J. Zhong and S.-C. Shi for low-temperature system maintenance, and T. Peng, Y. Cao, C.-Z. Peng and Y.-A. Chen for discussions. This work was supported by the National Key R&D Program of China (2017YFA0303900, 2017YFA0304000), the National Natural Science Foundation of China, the Chinese Academy of Sciences and the Anhui Initiative in Quantum Information Technologies.
Reviewer information
Nature thanks R. Colbeck and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
X.M., J.F., Q.Z. and J.-W.P. conceived the research. Y.L., X.M., J. F., Q.Z. and J.-W.P. designed the experiment. Y.L., M.-H.L. and C.W. designed and implemented the source of entangled photon pairs. W.-Z.L. and J.-Y.G. designed the data acquisition software. W.Z., H.L., Z.W. and L.Y. fabricated and characterized the superconducting nanowire single-photon detector. B.B. and J.Z. designed the quantum random-number generators for the measurement setting choices. Q. Zhao, X.Y. and X.M. performed the protocol analysis, numerical modelling and randomness extraction. Y.Z. and W.J.M. performed the hypothesis tests. All authors contributed to the experimental realization, data analysis and manuscript preparation. J.-W.P. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Text, Supplementary Figures 1-6, and Supplementary Tables 1-7. The Supplementary Information describes the theory of DIQRNG (Section I), the experimental details (Section II), and the experimental results (Section III).
Source data
Rights and permissions
About this article
Cite this article
Liu, Y., Zhao, Q., Li, MH. et al. Device-independent quantum random-number generation. Nature 562, 548–551 (2018). https://doi.org/10.1038/s41586-018-0559-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0559-3
Keywords
This article is cited by
-
Semi-device-independent quantum random number generator with a broadband squeezed state of light
npj Quantum Information (2024)
-
A comprehensive review of quantum random number generators: concepts, classification and the origin of randomness
Quantum Information Processing (2023)
-
Experimental entanglement quantification for unknown quantum states in a semi-device-independent manner
Science China Information Sciences (2023)
-
The expanding role of National Metrology Institutes in the quantum era
Nature Physics (2022)
-
A quantum random number generator on a nanosatellite in low Earth orbit
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.