Abstract
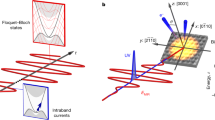
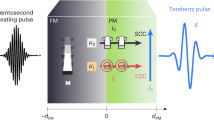
Harnessing the carrier wave of light as an alternating-current bias may enable electronics at optical clock rates1. Lightwave-driven currents have been assumed to be essential for high-harmonic generation in solids2,3,4,5,6, charge transport in nanostructures7,8, attosecond-streaking experiments9,10,11,12,13,14,15,16 and atomic-resolution ultrafast microscopy17,18. However, in conventional semiconductors and dielectrics, the finite effective mass and ultrafast scattering of electrons limit their ballistic excursion and velocity. The Dirac-like, quasi-relativistic band structure of topological insulators19,20,21,22,23,24,25,26,27,28,29 may allow these constraints to be lifted and may thus open a new era of lightwave electronics. To understand the associated, complex motion of electrons, comprehensive experimental access to carrier-wave-driven currents is crucial. Here we report angle-resolved photoemission spectroscopy with subcycle time resolution that enables us to observe directly how the carrier wave of a terahertz light pulse accelerates Dirac fermions in the band structure of the topological surface state of Bi2Te3. While terahertz streaking of photoemitted electrons traces the electromagnetic field at the surface, the acceleration of Dirac states leads to a strong redistribution of electrons in momentum space. The inertia-free surface currents are protected by spin–momentum locking and reach peak densities as large as two amps per centimetre, with ballistic mean free paths of several hundreds of nanometres, opening up a realistic parameter space for all-coherent lightwave-driven electronic devices. Furthermore, our subcycle-resolution analysis of the band structure may greatly improve our understanding of electron dynamics and strong-field interaction in solids.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors on request.
References
Krausz, F. & Stockman, M. I. Attosecond metrology: from electron capture to future signal processing. Nat. Photon. 8, 205–213 (2014).
Vampa, G. et al. Linking high-harmonics from gases and solids. Nature 522, 462–464 (2015).
Hohenleutner, M. et al. Real-time observation of interfering crystal electrons in high-harmonic generation. Nature 523, 572–575 (2015).
Langer, F. et al. Lightwave-driven quasiparticle collisions on a subcycle timescale. Nature 533, 225–229 (2016).
Garg, M. et al. Multi-petahertz electronic metrology. Nature 538, 359–363 (2016).
Liu, H. et al. High-harmonic generation from an atomically thin semiconductor. Nat. Phys. 13, 262–265 (2017).
Rybka, T. et al. Sub-cycle optical phase control of nanotunnelling in the single-electron regime. Nat. Photon. 10, 667–670 (2016).
Higuchi, T., Heide, C., Ullmann, K., Weber, H. B. & Hommelhoff, P. Light-field-driven currents in graphene. Nature 550, 224–228 (2017).
Miaja-Avila, L. et al. Laser-assisted photoelectric effect from surfaces. Phys. Rev. Lett. 97, 113604 (2006).
Cavalieri, A. L. et al. Attosecond spectroscopy in condensed matter. Nature 449, 1029–1032 (2007).
Schultze, M. et al. Attosecond band-gap dynamics in silicon. Science 346, 1348–1352 (2014).
Neppl, S. et al. Direct observation of electron propagation and dielectric screening on the atomic length scale. Nature 517, 342–346 (2015).
Locher, R. et al. Energy-dependent photoemission delays from noble metal surfaces by attosecond interferometry. Optica 2, 405–410 (2015).
Siek, F. et al. Angular momentum-induced delays in solid-state photoemission enhanced by intra-atomic interactions. Science 357, 1274–1277 (2017).
Feist, A. et al. Quantum coherent optical phase modulation in an ultrafast transmission electron microscope. Nature 521, 200–203 (2015).
Tao, Z. et al. Direct time-domain observation of attosecond final-state lifetimes in photoemission from solids. Science 353, 62–67 (2016).
Cocker, T. L. et al. An ultrafast terahertz scanning tunnelling microscope. Nat. Photon. 7, 620–625 (2013).
Cocker, T. L., Peller, D., Yu, P., Repp, J. & Huber, R. Tracking the ultrafast motion of a single molecule by femtosecond orbital imaging. Nature 539, 263–267 (2016).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Zhang, H. J. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009).
Kuroda, K., Reimann, J., Güdde, J. & Höfer, U. Generation of transient photocurrents in the topological surface state of Sb2Te3 by direct optical excitation with midinfrared pulses. Phys. Rev. Lett. 116, 076801 (2016).
Mahmood, F. et al. Selective scattering between Floquet–Bloch and Volkov states in a topological insulator. Nat. Phys. 12, 306–310 (2016).
Olbrich, P. et al. Room-temperature high-frequency transport of Dirac fermions in epitaxially grown Sb2Te3- and Bi2Te3-based topological insulators. Phys. Rev. Lett. 113, 096601 (2014).
Souma, S. et al. Direct measurement of the out-of-plane spin texture in the Dirac-cone surface state of a topological insulator. Phys. Rev. Lett. 106, 216803 (2011).
Sobota, J. A. et al. Ultrafast optical excitation of a persistent surface-state population in the topological insulator Bi2Se3. Phys. Rev. Lett. 108, 117403 (2012).
Kastl, C., Karnetzky, C., Karl, H. & Holleitner, A. W. Ultrafast helicity control of surface currents in topological insulators with near-unity fidelity. Nat. Commun. 6, 6617 (2015).
Minami, Y. et al. Terahertz-induced acceleration of massive Dirac electrons in semimetal bismuth. Sci. Rep. 5, 15870 (2015).
Braun, L. et al. Ultrafast photocurrents at the surface of the three-dimensional topological insulator Bi2Se3. Nat. Commun. 7, 13259 (2016).
Güdde, J., Rohleder, M., Meier, T., Koch, S. W. & Höfer, U. Time-resolved investigation of coherently controlled electric currents at a metal surface. Science 318, 1287–1291 (2007).
Hebling, J., Yeh, K.-L., Hoffmann, M. C., Bartal, B. & Nelson, K. A. Generation of high-power terahertz pulses by tilted-pulse-front excitation and their application possibilities. J. Opt. Soc. Am. B 25, 6–19 (2008).
Kokh, K. A. et al. Melt growth of bulk Bi2Te3 crystals with a natural p-n junction. CrystEngComm 16, 581–584 (2014).
Hecht, E. Optics 4th edn, Ch. 4 (Pearson Addison-Wesley, New York, 2012).
Richter, W., Köhler, H. & Becker, C.R. Raman and far-infrared investigation of phonons in the rhombohedral V2-VI3 compounds Bi2Te3, Bi2Se3, Sb2Te3 and Bi2(Te1−xSex)3 (0 < x < 1), (Bi1−ySby)2Te3 (0 < y < 1). Phys. Status Solidi B 84, 619–628 (1977).
Ziman, J. M. Principles of the Theory of Solids 2nd edn, Ch. 7 (Cambridge Univ. Press, Cambridge, 1979).
Gorbachuk, N. P. & Sidorko, V. R. Heat capacity and enthalpy of Bi2Si3 and Bi2Te3 in the temperature range 58–1012 K. Powder Metall. Met. Ceramics 43, 284–290 (2004).
Acknowledgements
We thank R. Höfer for discussions. The work in Marburg was supported by the Deutsche Forschungsgemeinschaft (DFG) through SFB 1083 and grant number HO 2295/7 (SPP 1666). Work in Regensburg was supported by the DFG through grant numbers HU 1598/2-1 and SFB 1277 (Project A05) and by the European Research Council through grant number 305003 (QUANTUMsubCYCLE). O.E.T. and K.A.K. were supported by the Russian Science Foundation (project number17-12-01047). A.K. was financially supported by KAKENHI number 17H06138.
Reviewer information
Nature thanks I. Katayama, S. Zhou and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
J.G., U.H. and R.H. conceived the study. J.R., S.S., C.P.S., F.L., S.B. and J.G. carried out the experiment. K.A.K., O.E.T. and A.K. provided the samples and performed the transport measurements. J.R., C.L., J.G. and U.H. carried out the theoretical modelling. All authors analysed the data, discussed the results and contributed to writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Optical set-up.
a, THz generation via tilted pulse fronts in lithium niobate (LiNbO3). After the laser beam from the titanium:sapphire amplifier system has been reduced in diameter by a reflective telescope, a grating (G) induces a pulse front tilt. Cylindrical lenses (CL) image and focus the beam into a cryogenically cooled LiNbO3 crystal, where optical rectification generates intense THz radiation. A pair of wire-grid polarizers (P) controls the polarization state. b, Electro-optically detected THz waveform after transmission through the fused silica window of the vacuum chamber. Inset, amplitude spectrum of the transient shown in a. c, Set-up for generating UV pulses for photoemission. A lens (L; focal length, 1 m) gently focuses the fundamental titanium:sapphire pulses. A beam splitter (BS) separates 90% of the intensity for second-harmonic generation in a BBO crystal (SHG-BBO). Subsequent dispersion and polarization control is employed using a birefringent calcite plate and a dual-half-wave plate (Dual-λ/2). The third harmonic is generated in another BBO crystal (THG-BBO), separated from the fundamental pulses with a beam splitter (BS), and spatially and temporally (Delay) overlapped with the remaining fundamental pulses to generate the sum-frequency at the fourth harmonic (FHG-BBO). d, The resulting spectrum of the fourth harmonic is centred at λc = 201 nm with a full-width at half-maximum (FWHM) of 2.8 nm, corresponding to a Fourier limit of 22 fs.
Extended Data Fig. 2 Determination of the reflectivity of Bi2Te3.
a, Electro-optically detected THz transients after reflection off a Bi2Te3 (red) and a gold reference (blue) surface kept at a temperature of 77 K. b, Amplitude spectra of the field traces in a normalized to the amplitude of the gold spectrum. c, Reflection coefficient rp (black spheres) for parallel incidence obtained by dividing the amplitude spectra from Bi2Te3 and gold. The orange curve describes the reflection coefficient rp calculated using the corresponding Fresnel formula with a Drude–Lorentz model for the dielectric function of Bi2Te3 (see equation (1)). d, Transmission coefficient ts calculated using the modelled dielectric function.
Extended Data Fig. 3 Comparison of scattering mechanisms.
a–l, Calculated distribution functions at different delay times t for the experimental THz waveform with an amplitude of 2.4 kV cm−1. Experimental broadening is not accounted for. The Boltzmann equation used to compute these results includes only the relaxation term (a–f) or only the effective backscattering term (g–l).
Extended Data Fig. 4 Broadening of the electron distribution.
a–c, Experimental distribution functions (red and blue circles) for different delay times t compared to the equilibrium Fermi–Dirac distribution (solid black line).
Extended Data Fig. 5 Local current density in Bi2Te3.
a, Calculated current density j (colour scale) as a function of the delay time t and the electron excursion in the surface layer of Bi2Te3. The excursion was evaluated using the extracted scattering times of the charge carriers within the topologically protected surface state. The intense THz fields coherently drive Dirac fermions over several hundred nanometres before they undergo scattering. b, The red solid curve shows the simulated current dynamics calculated for scattering times of \({\tau }_{{\rm{R}}}={\tau }_{k\bar{k}}=1\hspace{2.22144pt}{\rm{ps}}\); the THz electric field is depicted as a dashed black curve.
Supplementary information
Video 1
Time-domain video of THz-accelerated Dirac fermions in the surface 2 bands of Bi2Te3. a, Angle-resolved photoemission spectra of the topologically protected surface band in Bi2Te3 as a function of the delay time, t, between an s-polarized THz field and the UV probe. The THz electric field directly accelerates Dirac fermions within the bands, transiently inducing an asymmetric occupation in momentum space and a net electron current flowing on the sample surface. b, THz waveform ETHz as retrieved via momentum streaking of the photoemitted electrons. The blue sphere traces the delay time of the respective photoemission spectrum shown in a.
Rights and permissions
About this article
Cite this article
Reimann, J., Schlauderer, S., Schmid, C.P. et al. Subcycle observation of lightwave-driven Dirac currents in a topological surface band. Nature 562, 396–400 (2018). https://doi.org/10.1038/s41586-018-0544-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0544-x
Keywords
This article is cited by
-
Attosecond electron microscopy by free-electron homodyne detection
Nature Photonics (2024)
-
Build-up and dephasing of Floquet–Bloch bands on subcycle timescales
Nature (2023)
-
Attosecond magnetization dynamics in non-magnetic materials driven by intense femtosecond lasers
npj Computational Materials (2023)
-
Giant room-temperature nonlinearities in a monolayer Janus topological semiconductor
Nature Communications (2023)
-
Terahertz control of many-body dynamics in quantum materials
Nature Reviews Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.