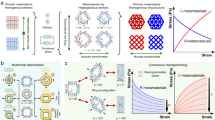
Abstract
Multi-step pathways—which consist of a sequence of reconfigurations of a structure—are central to the functionality of various natural and artificial systems. Such pathways execute autonomously in self-guided processes such as protein folding1 and self-assembly2,3,4,5, but have previously required external control to execute in macroscale mechanical systems, provided by, for example, actuators in robotics6,7,8,9 or manual folding in origami8,10,11,12. Here we demonstrate shape-changing, macroscale mechanical metamaterials that undergo self-guided, multi-step reconfiguration in response to global uniform compression. We avoid the need for external control by using metamaterials that are made purely of passive components. The design of the metamaterials combines nonlinear mechanical elements with a multimodal architecture that enables a sequence of topological reconfigurations caused by the formation of internal self-contacts between the elements of the metamaterial. We realize the metamaterials by using computer-controlled water-jet cutting of flexible materials, and show that the multi-step pathway and final configuration can be controlled by rational design of the nonlinear mechanical elements. We also demonstrate that the self-contacts suppress errors in the pathway. Finally, we create hierarchical architectures to extend the number of distinct reconfiguration steps. Our work establishes general principles for designing mechanical pathways, opening up new avenues for self-folding media11,12, pluripotent materials9,13 and pliable devices14 in areas such as stretchable electronics and soft robotics15.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data and code availability
The data shown in the figures and the data and code that support the other findings of this study are available from the corresponding author on request.
References
Dobson, C. M. Protein folding and misfolding. Nature 426, 884–890 (2003).
Winfree, E., Liu, F., Wenzler, L. A. & Seeman, N. C. Design and self-assembly of two-dimensional DNA crystals. Nature 394, 539–544 (1998).
Wei, B., Dai, M. & Yin, P. Complex shapes self-assembled from single-stranded DNA tiles. Nature 485, 623–626 (2012).
Chen, Q., Bae, S. C. & Granick, S. Directed self-assembly of a colloidal kagome lattice. Nature 469, 381–384 (2011).
Zeravcic, Z. & Brenner, M. P. Self-replicating colloidal clusters. Proc. Natl Acad. Sci. USA 111, 1748–1753 (2014).
Zykov, V., Mytilinaios, E., Adams, B. & Lipson, H. Robotics: self-reproducing machines. Nature 435, 163–164 (2005).
Shepherd, R. F. et al. Multigait soft robot. Proc. Natl Acad. Sci. USA 108, 20400–20403 (2011).
Felton, S., Tolley, M., Demaine, E., Rus, D. & Wood, R. Applied origami. a method for building self-folding machines. Science 345, 644–646 (2014).
Overvelde, J. T., Weaver, J. C., Hoberman, C. & Bertoldi, K. Rational design of reconfigurable prismatic architected materials. Nature 541, 347–352 (2017).
Waitukaitis, S., Menaut, R., Chen, B. G. & van Hecke, M. Origami multistability: from single vertices to metasheets. Phys. Rev. Lett. 114, 055503 (2015).
Pinson, M. B. et al. Self-folding origami at any energy scale. Nat. Commun. 8, 15477 (2017).
Stern, M., Pinson, M. & Murugan, A. The difficulty of folding self-folding origami. Phys. Rev. X 7, 041070 (2017).
Cho, Y. et al. Engineering the shape and structure of materials by fractal cut. Proc. Natl Acad. Sci. USA 111, 17390–17395 (2014).
Xu, S. et al. Materials science: assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling. Science 347, 154–159 (2015).
Rogers, J., Huang, Y., Schmidt, O. G. & Gracias, D. H. Origami mems and nems. MRS Bull. 41, 123–129 (2016).
Bertoldi, K., Vitelli, V., Christensen, J. & van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2, 17066 (2017).
Bertoldi, K., Reis, P. M., Willshaw, S. & Mullin, T. Negative Poisson’s ratio behavior induced by an elastic instability. Adv. Mater. 22, 361–366 (2010).
Huber, S. D. Topological mechanics. Nat. Phys. 12, 621–623 (2016).
Coulais, C., Sounas, D. & Alú, A. Static nonreciprocity in mechanical metamaterials. Nature 542, 461–464 (2017).
Coulais, C., Teomy, E., de Reus, K., Shokef, Y. & van Hecke, M. Combinatorial design of textured mechanical metamaterials. Nature 535, 529–532 (2016).
Grima, J. N. & Evans, K. E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 19, 1563–1565 (2000).
Mullin, T., Deschanel, S., Bertoldi, K. & Boyce, M. C. Pattern transformation triggered by deformation. Phys. Rev. Lett. 99, 084301 (2007).
Coulais, C., Kettenis, C. & van Hecke, M. A characteristic length scale causes anomalous size effects and boundary programmability in mechanical metamaterials. Nat. Phys. 14, 40–44 (2018).
Gatt, R. et al. Hierarchical auxetic mechanical metamaterials. Sci. Rep. 5, 8395 (2015).
Tang, Y. et al. Design of hierarchically cut hinges for highly stretchable and reconfigurable metamaterials with enhanced strength. Adv. Mater. 27, 7181–7190 (2015).
Mousanezhad, D. et al. Hierarchical honeycomb auxetic metamaterials. Sci. Rep. 5, 18306 (2015).
Overvelde, J. T. et al. A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of freedom. Nat. Commun. 7, 10929 (2016).
Coulais, C., Overvelde, J. T. B., Lubbers, L. A., Bertoldi, K. & van Hecke, M. Discontinuous buckling of wide beams and metabeams. Phys. Rev. Lett. 115, 044301 (2015).
Blees, M. K. et al. Graphene kirigami. Nature 524, 204–207 (2015).
Zhang, Y. et al. A mechanically driven form of kirigami as a route to 3D mesostructures in micro/nanomembranes. Proc. Natl Acad. Sci. USA 112, 11757–11764 (2015).
Coulais, C. Periodic cellular materials with nonlinear elastic homogenized stress-strain response at small strains. Int. J. Solids Struct. 97–98, 226–238 (2016).
Acknowledgements
We thank J. Mesman and D. Ursem for technical support. We acknowledge Z. Zeravcic and A. Murugan for discussions. We acknowledge funding from the Netherlands Organization for Scientific Research through grants VICI No. NWO-680-47-609 (M.v.H.) and VENI NWO-680-47-445 (C.C).
Reviewer information
Nature thanks L. Howell and L. Valdevit for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
All authors conceived the project. C.C. and M.v.H. developed the theoretical models and C.C. performed the numerical simulations. C.C., A.S. and F.V. designed and carried out the experiments. C.C. and M.v.H. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Multimodal hierarchical mechanical metamaterials.
a, 4 × 4 rotating-square mechanism, which has a zero mode corresponding to counter-rotation of each square unit as indicated. b–d, Hierarchical construction of a box fractal, where in each generation a square is replaced by a cross-like pattern of five smaller squares. Red, blue and green links correspond to α links that connect different units, internal β links that occur for rank m ≥ 2 and γ links that occur for rank m ≥ 3, respectively.
Extended Data Fig. 2 Hinged tessellations.
a, Free motion of the rotating-square mechanism. b, Free motion of rotating-square mechanism with unequal squares. c, Free motion of linked crosses.
Extended Data Fig. 3 Kinematics and orthogonal basis of zero-energy motions of a 2 × 2 super-cell with square periodic boundary conditions.
a, Definition of the bending angles \(\{{\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4},\alpha {^{\prime} }_{1},\alpha {^{\prime} }_{2},\alpha {^{\prime} }_{3},\alpha {^{\prime} }_{4}\}\). The grey squares depict the periodic boundary conditions. b, Definition of the angles {β1, β2, …, β16}. c, d, The motions A–F form an orthogonal basis of deformations. c, Schematic representation. Red denotes hinging of the α links. Light (dark) blue denotes clockwise (anticlockwise) hinging of the β links. d, Vector representation. The row of the table correspond to the vectors mA,…,F = {α1, …, α4, \(\alpha {^{\prime} }_{1}\), …, \(\alpha {^{\prime} }_{4}\), β1, …, β16} that form the basis of all possible motions A–F.
Extended Data Fig. 4 Mode analysis for a 2 × 2 super-cell with square periodic boundary conditions.
Unless noted otherwise, all data are for tα + tβ = 3 mm; data for other normalizations look extremely similar. a, Eigenfrequencies of the first linear eigenmodes as functions of tα/tβ. b, Normalized projection of the lowest eigenmode onto motions A–F. To calculate the normalized projections, we compute the inner products between the bending-angle vectors b and the vectors mA,…,F defined in Extended Data Fig. 3 and normalize them by the sum of all inner products. c, Critical buckling strain as a function of tα/tβ, for tα + tβ = 1 mm, 2 mm and 3 mm (dotted, dashed and solid lines, respectively). The value of the critical strain depends on tα + tβ, but the crossover does not. d, Normalized projection of the buckling mode onto motions A–F, for tα + tβ = 1 mm, 2 mm and 3 mm (dotted, dashed and solid lines, respectively). We calculate the normalized projections as in c.
Extended Data Fig. 5 Nonlinear analysis with symmetry-broken links on a 2 × 2 super-cell with square periodic boundary conditions.
a, b, Snapshots of the super-cell in the un-deformed (left) and deformed (strain of 6.6%; right) states, for tα = 0.9 and tβ = 2.1 (a) and tα = 2.1 and tβ = 0.9 (b). In both cases, the offset of the β links is 0.5tβ. c, d, Projection of the deformed states b · mA (c) and b · mB (d) versus strain ε for tα/tβ ranging from 0.2 (blue) to 15 (red) and tα + tβ = 3 mm. The case tα/tβ = 2.3, which is close to the experimental value (tα/tβ = 2.5, Fig. 2e–h) is highlighted by a thick yellow line.
Extended Data Fig. 6 Metamaterial under compression with tα = 4 mm and tβ = 1 mm.
Stills of the compression experiment are shown for strains of ε = 0 (left), 0.24 (middle) and 0.52 (right). In the middle panel, the light (dark) blue dots indicate clockwise (anticlockwise) hinging of the β links, similar to motion B that initiates pathway II, but with substantial disorder near the boundaries that penetrate into the bulk.
Extended Data Fig. 7 Sample geometry.
A close-up of the computer-assisted design of the rank-2 metamaterial is shown for the sample in Fig. 2a–d.
Extended Data Fig. 8 Compression device.
The custom-made compression fixture applies biaxial compression using a uniaxial testing device.
Extended Data Fig. 9 Effect of boundaries on angles.
a, b, Bending of the links for larger regions of the sample than shown in the main text: α (red) and β (blue) versus strain ε for the central 64 squares (excluding the outermost 16 squares) (a); α (red), β (blue) and γ (green) versus strain ε for the central 165 squares (excluding the outermost 60 squares) (b). Grey shading indicates one standard deviation and the angles are based on the same runs as in Fig. 2a–d (a) or Fig. 3 (b).
Extended Data Fig. 10 Alternative topologies.
a, Linked squares with edges of 4.5 mm and link thicknesses of t0 = 1.35 mm, tα = 0.45 mm, \(t{^{\prime} }_{\alpha }\) = 0.45 mm, tβ = 0.9 mm and \(t{^{\prime} }_{\beta }\) = 0.68 mm, showing a two-step folding pathway under uniaxial compression. b, Structure of linked squares with edges of 4.5 mm and link thicknesses of tα = 0.45 mm, \(t{^{\prime} }_{\alpha }\) = 0.45 mm, tβ = 0.9 mm and \(t{^{\prime} }_{\beta }\) = 0.9 mm connected by slanted bars of thickness 4.5 mm, showing a two-step folding pathway under uniaxial compression.
Supplementary information
Video 1
Videos of the different pathways experienced by rank-two metamaterials with various hinges geometries under equi-biaxial compression (See Main text Fig. 1-2). The detected ellipses are overlaid on top of the raw images.
Video 2
Video of the three-step pathway experienced by a rank-three metamaterials under equi-biaxial compression (See Main text Fig. 3). The detected ellipses are overlaid on top of the raw images.
Source data
Rights and permissions
About this article
Cite this article
Coulais, C., Sabbadini, A., Vink, F. et al. Multi-step self-guided pathways for shape-changing metamaterials. Nature 561, 512–515 (2018). https://doi.org/10.1038/s41586-018-0541-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0541-0
Keywords
This article is cited by
-
Zero modes activation to reconcile floppiness, rigidity, and multistability into an all-in-one class of reprogrammable metamaterials
Nature Communications (2024)
-
Embedded shape morphing for morphologically adaptive robots
Nature Communications (2023)
-
Hydrogel muscles powering reconfigurable micro-metastructures with wide-spectrum programmability
Nature Materials (2023)
-
Strong conformable structure via tension activated kirigami
Communications Materials (2023)
-
Engineering zero modes in transformable mechanical metamaterials
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.