Abstract
Essential biological functions, such as mitosis, require tight coordination of hundreds of proteins in space and time. Localization, the timing of interactions and changes in cellular structure are all crucial to ensure the correct assembly, function and regulation of protein complexes1,2,3,4. Imaging of live cells can reveal protein distributions and dynamics but experimental and theoretical challenges have prevented the collection of quantitative data, which are necessary for the formulation of a model of mitosis that comprehensively integrates information and enables the analysis of the dynamic interactions between the molecular parts of the mitotic machinery within changing cellular boundaries. Here we generate a canonical model of the morphological changes during the mitotic progression of human cells on the basis of four-dimensional image data. We use this model to integrate dynamic three-dimensional concentration data of many fluorescently knocked-in mitotic proteins, imaged by fluorescence correlation spectroscopy-calibrated microscopy5. The approach taken here to generate a dynamic protein atlas of human cell division is generic; it can be applied to systematically map and mine dynamic protein localization networks that drive cell division in different cell types, and can be conceptually transferred to other cellular functions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All images processed in this study including original images, concentration maps, segmentation mask for both cellular and chromosomal volume and concentration maps are available in the Image Data Resource (http://idr.openmicroscopy.org51) under DOI: 10.17867/10000112. Further data and code are available as follows: all images are also available for download on the mitotic cell atlas website http://www.mitocheck.org/mitotic_cell_atlas/downloads/v1.0.1/mitotic_cell_atlas_v1.0.1_fulldata.zip (~0.5 TB).The data supporting the spatio-temporal mitotic cell model and the analysis is available from the mitotic cell atlas website (http://www.mitocheck.org/mitotic_cell_atlas/downloads/v1.0.1) and contains: i) segmentation masks for the landmarks (that is, cell boundary and chromosome mass(es)) as TIFF files (directory ‘mitotic_cell_model/binary_masks’) and snapshots of the 3D rendering of each of the spatial models in VRML and TIFF formats (directory ‘mitotic_cell_model/snapshots’). ii) Two movies (orthogonal and oblique views) created from 3D reconstructed average landmarks (cell boundary and chromosome mass(es); directory ‘mitotic_cell_model/movies’). iii) Average concentrations of each protein at individual mitotic stages as mat files, TIFF stacks, and tab-delimited text files (directory ‘protein_distributions’). iv) Feature data used for the analysis (to produce Fig. 4, Extended Data Figs. 7, 8d, e, 9) in a tab-delimited text file (file ‘cell_features.txt’). This file can be used directly as input to the notebooks available in the code repository. This file also contains the mitotic standard time and stage assigned to each cell image. v) Canonical localization data (file ‘canonical_mitotic_clusters.h5’). vi) Dynamic graph (file ‘dynamic_graph_adjacency_matrices.h5’).
References
Rodriguez-Bravo, V. et al. Nuclear pores protect genome integrity by assembling a premitotic and Mad1-dependent anaphase inhibitor. Cell 156, 1017–1031 (2014).
Dick, A. E. & Gerlich, D. W. Kinetic framework of spindle assembly checkpoint signalling. Nat. Cell Biol. 15, 1370–1377 (2013).
Ghongane, P., Kapanidou, M., Asghar, A., Elowe, S. & Bolanos-Garcia, V. M. The dynamic protein Knl1—a kinetochore rendezvous. J. Cell Sci. 127, 3415–3423 (2014).
Fink, J. et al. External forces control mitotic spindle positioning. Nat. Cell Biol. 13, 771–778 (2011).
Politi, A. Z. et al. Quantitative mapping of fluorescently tagged cellular proteins using FCS-calibrated four-dimensional imaging. Nat. Protocols 13, 1445–1464 (2018).
Koch, B. et al. Generation and validation of homozygous fluorescent knock-in cells using CRISPR-Cas9 genome editing. Nat. Protocols 13, 1465–1487 (2018).
Magde, D., Elson, E. & Webb, W. W. Thermodynamic fluctuations in a reacting system measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 29, 705–708 (1972).
Hockemeyer, D. et al. Efficient targeting of expressed and silent genes in human ESCs and iPSCs using zinc-finger nucleases. Nat. Biotechnol. 27, 851–857 (2009).
Cong, L. et al. Multiplex genome engineering using CRISPR/Cas systems. Science 339, 819–823 (2013).
Poser, I. et al. BAC TransgeneOmics: a high-throughput method for exploration of protein function in mammals. Nat. Methods 5, 409–415 (2008).
Alberts, B. et al. Molecular Biology of the Cell 4th Edition (Garland Science, New York, 2002).
Landry, J. J. M. et al. The genomic and transcriptomic landscape of a HeLa cell line. G3 (Bethesda) 3, 1213–1224 (2013).
Holzmann, J., Fuchs, J., Pichler, P., Peters, J. M. & Mechtler, K. Lesson from the stoichiometry determination of the cohesin complex: a short protease mediated elution increases the recovery from cross-linked antibody-conjugated beads. J. Proteome Res. 10, 780–789 (2011).
Burke, L. J. et al. CTCF binding and higher order chromatin structure of the H19 locus are maintained in mitotic chromatin. EMBO J. 24, 3291–3300 (2005).
Mora-Bermúdez, F., Gerlich, D. & Ellenberg, J. Maximal chromosome compaction occurs by axial shortening in anaphase and depends on Aurora kinase. Nat. Cell Biol. 9, 822–831 (2007).
Otsuka, S. et al. Nuclear pore assembly proceeds by an inside-out extrusion of the nuclear envelope. eLife 5, e19071 (2016).
Otsuka, S. et al. Postmitotic nuclear pore assembly proceeds by radial dilation of small membrane openings. Nat. Struct. Mol. Biol. 25, 21–28 (2018).
Bay, H., Ess, A., Tuytelaars, T. & Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 110, 346–359 (2008).
Carmena, M., Wheelock, M., Funabiki, H. & Earnshaw, W. C. The chromosomal passenger complex (CPC): from easy rider to the godfather of mitosis. Nat. Rev. Mol. Cell Biol. 13, 789–803 (2012).
Hauf, S. et al. The small molecule Hesperadin reveals a role for Aurora B in correcting kinetochore-microtubule attachment and in maintaining the spindle assembly checkpoint. J. Cell Biol. 161, 281–294 (2003).
Steigemann, P. et al. Aurora B-mediated abscission checkpoint protects against tetraploidization. Cell 136, 473–484 (2009).
Isokane, M. et al. ARHGEF17 is an essential spindle assembly checkpoint factor that targets Mps1 to kinetochores. J. Cell Biol. 212, 647–659 (2016).
Bodor, D. L. et al. The quantitative architecture of centromeric chromatin. eLife 3, e02137 (2014).
Gascoigne, K. E. & Cheeseman, I. M. CDK-dependent phosphorylation and nuclear exclusion coordinately control kinetochore assembly state. J. Cell Biol. 201, 23–32 (2013).
Maliga, Z. et al. A genomic toolkit to investigate kinesin and myosin motor function in cells. Nat. Cell Biol. 15, 325–334 (2013).
Hutchins, J. R. et al. Systematic analysis of human protein complexes identifies chromosome segregation proteins. Science. 328, 593–599 (2010).
Kunitoku, N. et al. CENP-A phosphorylation by Aurora-A in prophase is required for enrichment of Aurora-B at inner centromeres and for kinetochore function. Dev. Cell 5, 853–864 (2003).
Mahen, R. et al. Comparative assessment of fluorescent transgene methods for quantitative imaging in human cells. Mol. Biol. Cell 25, 3610–3618 (2014).
Walther, N. et al. A quantitative map of human Condensins provides new insights into mitotic chromosome architecture. J. Cell Biol. 217, 2309–2328 (2018).
Ladurner, R. et al. Sororin actively maintains sister chromatid cohesion. EMBO J. 35, 635–653 (2016).
Davidson, I. F. et al. Rapid movement and transcriptional re-localization of human cohesin on DNA. EMBO J. 35, 2671–2685 (2016).
Neumann, B. et al. Phenotypic profiling of the human genome by time-lapse microscopy reveals cell division genes. Nature 464, 721–727 (2010).
Bancaud, A. et al. Molecular crowding affects diffusion and binding of nuclear proteins in heterochromatin and reveals the fractal organization of chromatin. EMBO J. 28, 3785–3798 (2009).
Li, C. H. & Lee, C. K. Minimum cross entropy thresholding. Pattern Recognit. 26, 617–625 (1993).
Hériché, J.-K. et al. Integration of biological data by kernels on graph nodes allows prediction of new genes involved in mitotic chromosome condensation. Mol. Biol. Cell 25, 2522–2536 (2014).
Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 9, 62–66 (1979).
Meyer, F. Topographic distance and watershed lines. Signal Processing 38, 113–125 (1994).
Wachsmuth, M. et al. High-throughput fluorescence correlation spectroscopy enables analysis of proteome dynamics in living cells. Nat. Biotechnol. 33, 384–389 (2015).
Ori, A. et al. Cell type-specific nuclear pores: a case in point for context-dependent stoichiometry of molecular machines. Mol. Syst. Biol. 9, 648 (2013).
Barton, G. J. & Sternberg, M. J. E. A strategy for the rapid multiple alignment of protein sequences. Confidence levels from tertiary structure comparisons. J. Mol. Biol. 198, 327–337 (1987).
ten Holt, G., Reinders, M. & Hendriks, E. Multi-dimensional dynamic time warping for gesture recognition. In Proc. 13th Annual Conference of the Advanced School for Computing and Imaging (2007).
Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. 29, 1153–1160 (1981).
Lazebnik, S., Schmid, C. & Ponce, J. A sparse texture representation using local affine regions. IEEE Trans. Pattern Anal. Mach. Intell. 27, 1265–1278 (2005).
Heikkilä, M. & Pietikäinen, M. A texture-based method for modeling the background and detecting moving objects. IEEE Trans. Pattern Anal. Mach. Intell. 28, 657–662 (2006).
Tran, T. N., Drab, K. & Daszykowski, M. Revised DBSCAN algorithm to cluster data with dense adjacent clusters. Chemom. Intell. Lab. Syst. 120, 92–96 (2013).
Jolliffe, I. T. Principal Component Analysis (Springer, New York, 2002).
Lee, D. D. & Seung, H. S. Learning the parts of objects by non-negative matrix factorization. Nature 401, 788–791 (1999).
Cichocki, A., Zdunek, R., Phan, A. H. & Amari, S.-I. Nonnegative Matrix and Tensor Factorizations (John Wiley & Sons, Chichester, 2009).
Tucker, L. R. A Method for Synthesis of Factor Analysis Studies (Educational Testing Service, Princeton, 1951).
Aitchison, J. The Statistical Analysis of Compositional Data (Blackburn Press, Caldwell, 2003).
Williams, E. et al. Image Data Resource: a bioimage data integration and publication platform. Nat. Methods 14, 775–781 (2017).
Zuin, J. et al. A cohesin-independent role for NIPBL at promoters provides insights in CdLS. PLoS Genetics 10, e1004153 (2014).
Acknowledgements
We thank T. Hyman and I. Poser for donating multiple mouse BAC protein–GFP cell lines and T. Hirota for giving us the eGFP–CENPA cell line. The automatic imaging would not have been possible without R. Höfler and D. W. Gerlich, who developed the Micronaut software. We thank all members of the Ellenberg and Peters laboratories for support, especially M. Isokane, M. J. Roberti, J. Mergenthaler, S. Otsuka, W. Tang and D. Cisneros for generating cell lines, reagents and constructs. We thank A. Callegari for supporting the U2OS data generation. We also thank W. Huber, B. Fischer, B. Klaus and L. P. Coelho for discussions, the EMBL mechanical and electronic workshop, the EMBL advanced light microscopy facility, the EMBL flow cytometry core facility and the IMP BioOptics Facility for their support. This study has benefited from the collaboration with Carl ZEISS Jena, especially with T. Ohrt. The work was supported by grants from EU-FP7-MitoSys (Grant Agreement 241548) to J.E. and J.M.P., EU-FP7-SystemsMicroscopy NoE (Grant Agreement 258068), EU-H2020-iNEXT (Grant Agreement 653706) and the 4D Nucleome/4DN National Institutes of Health common fund (5 U01 EB021223-04 / 8 U01 DA047728-04) all to J.E., as well as by the European Molecular Biology Laboratory (Y.C., M.J.H., J.-K.H., A.Z.P., N.W., B.K., M.W., B.N., M.K., S.A. and J.E.). Y.C. and N.W. were also supported by the EMBL International PhD Programme (EIPP). Research in the laboratory of J.M.P. was further supported by Boehringer Ingelheim, the Austrian Science Fund (FWF special research program SFB F34 ‘Chromosome Dynamics’ and Wittgenstein award Z196-B20), the Austrian Research Promotion Agency (Headquarter grants FFG-834223 and FFG-852936) and the European Research Council (ERC) under the European Union Horizon 2020 research and innovation programme (Grant Agreement 693949).
Reviewer information
Nature thanks R. Murphy, J. Swedlow and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
B.K., B.N., M.K., R.L., M.M.K. and N.W. constructed and validated GFP knock-in cell lines. Y.C., A.Z.P. and M.W. developed the imaging pipeline. Y.C., A.Z.P. and N.W. performed the calibrated live-cell imaging. Y.C., M.J.H., J.-K.H. and A.Z.P. developed the computational analysis pipeline. Y.C., J.-K.H., M.J.H., A.Z.P., S.A. and J.E. wrote the manuscript. J.M.P. coordinated the MitoSys consortium and supervised part of the work. J.E. supervised the work overall and originally conceived the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Segmentation and time alignment.
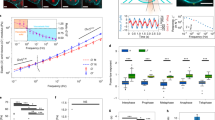
a, b, Segmentation and 3D reconstruction of landmarks. a, Single x–y plane image in mCherry (587–621 nm, first row) and DY481XL (622–695 nm, second row) detection channels. Third row: detected chromatin markers in which boundaries of the chromosomal volume of interest are marked in red. Fourth row: output of watershed transform on ratio image in which the boundary of the detected cell of interest is marked in green. Scale bar, 10 μm. b, Reconstruction of cell and chromosomal surfaces in 3D (grey) and the predicted division axis (red). c–e, Generating the mitotic standard time model. c, Dynamic time warping is used to align a pair of time-resolved sequences. d, Modified Barton–Sternberg algorithm to align 132 sequences. e, The cumulative s.d. of a single feature after each iteration of the algorithm. It remains nearly constant after the second round indicating that at termination (fourth round) a stable time alignment was achieved. This has been repeated 10 times and similar alignment results are obtained when the number of cells is more than 50.
Extended Data Fig. 2 Detection of mitotic standard stages.
a, Detection of major mitotic transitions of the mitotic standard time. Peaks in the second derivatives (red circles) above a pre-defined threshold (grey lines) were detected in all feature dimensions as mitotic transitions. b, Additional smaller peaks (blue dots) were detected to ensure a maximum duration of 12 min for each standard stage. c, Transitions were deleted (grey circles) such that all stages had a minimal duration of 1.5 min. d, The standard mitotic cell was represented by the cell closest to the mean of each stage. Each mitotic stage was assigned duration (coloured line), its duration s.d. (grey line) and a biological annotation.
Extended Data Fig. 3 Comparison between mitotic standard time for HeLa Kyoto and U2OS cells.
a, Features used for generating the mitotic standard time model after alignment for HeLa Kyoto cells (left) and U2OS cells (right). Grey line, normalized feature value over time of individual cells; black line, mean. b, Mitotic standard time transitions for HeLa cells (left) and U2OS cells (right). c, Standard mitotic U2OS cell represented by the cell closest to the average of each mitotic standard stage. Each mitotic stage was assigned duration (coloured line), its duration s.d. (grey line) and a biological annotation.
Extended Data Fig. 4 Generation of spatial model for standard mitotic stages by combining two cylindrical representations.
a, b, Examples of cells in mitotic stage 10 (a) were registered using the predicted cell division axis as shown in b. c, Transformation between Cartesian and cylindrical coordinate systems. d, Example cellular and chromosomal surfaces (grey) were transformed into the cylindrical coordinate system using two cylindrical axes (z-axis or predicted division axis) marked in yellow. e, Average cellular and chromosomal surfaces in cylindrical coordinate systems. f, Union (∪) and intersection (∩) of the averaged landmarks volumes represented in the Cartesian coordinate system that were then combined to generate final cellular and chromosomal surfaces shown in the first image in g. g, By averaging a large number of cells, models were generated for all mitotic standard stages with symmetrical geometries and example stages 10, 14, 16 and 19 are shown. h, The spatial variation of the mitotic standard spaces shown in g.
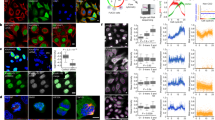
Extended Data Fig. 5 Chromatin organizers and NUPs localization.
a–c, Maximal intensity projection from the mitotic standard model at selected stages. Scale bars, 10 μm. a, Chromatin organizers RAD21, CTCF, NCAPH2, KIF4A and TOP2A present on chromatin during mitosis. b, Chromatin organizers STAG1, STAG2 and WAPL with weak binding to chromatin during mitosis. c, Four NUPs at selected standard mitotic stages. d, NUPs localization as function of mitotic standard time. The curves for STAG2 and WAPL are shown as a reference and are identical to the data from Fig. 3c.
Extended Data Fig. 6 Interest point clusters and dynamic protein localization.
a, Pipeline for the definition of interest point clusters using a subset of the data. Images (936, corresponding to 5% of the entire dataset) were randomly selected from the dataset to construct a pool of interest points. Each interest point was numerically described with a 40 dimensional feature vector encoding the intensity distribution, localization and contrasts to the interest point neighbourhood. Combining k-d tree-like and thresholding-based clustering with density-based clustering, the interest points were grouped into 100 clusters. b, The remaining interest points of the dataset were then assigned to the identified clusters. Thus each image was represented as the distribution of intensity in each of the 100 interest point clusters. c, Non-negative factorization of the data tensor of proteins × features × mitotic stages (left panel) produced a non-negative tensor of reduced dimension (middle) for which entries can be interpreted as the fraction of protein belonging to each cluster over time (right, each cluster is represented by a different colour and the height of a coloured bar at a given mitotic stage represents the fraction of the protein in the corresponding cluster at this stage).
Extended Data Fig. 7 Quantitative evolution of protein subcellular localizations inferred from non-negative tensor factorization of the proteins × features × time tensor.
Each subcellular localization cluster was assigned a different colour and named using known information on proteins belonging to that cluster. The height of each colour band at each time point is proportional to the fraction of the protein amount in the corresponding cluster at that time point. Genes were grouped by complete linkage clustering with optimal leaf ordering.
Extended Data Fig. 8 Mitotic standard model and supervised classification to investigate the dynamic localization of kinetochore proteins.
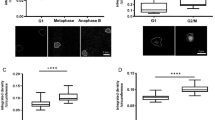
a, b, Concentration maps of chromosome passenger complex proteins AURKB and CDCA8 in anaphase and early telophase. a, AURKB concentrates in an outer ring and a central disk. Most of CDCA8 remains on chromatin, and after AURKB has already relocalized—between late anaphase and early telophase—only a small CDCA8 fraction colocalizes with AURKB in the central disk. b, Colour displaying CDCA8 was adapted to make its localization in the central disk visible. c–e, Analysing sub-cellular (dis)assembly kinetics using a supervised approach. c, Example of maximally z-projected images of marker proteins for the selected subcellular compartments used for the supervised approach. Scale bar, 10 μm. d, Kinetics of kinetochore disassembly. The predicted number of molecules localized on kinetochore and centromeres are plotted for eight proteins in the mitotic standard time (left) and zoomed in for anaphase (right). e, Order and rate of protein removal from the kinetochore during anaphase. The annotation and circle diameter indicate the number of molecules at the estimated average time of dissociation.
Extended Data Fig. 9 Prediction of protein molecule numbers on major mitotic subcellular structures using the supervised approach.
The colour scheme is adjusted to the most similar cluster identified using non-negative tensor factorization (Extended Data Fig. 7). Cytoplasm values are divided by ten.
Supplementary information
Supplementary Information
This file contains Supplementary Table 1, a list of cell lines and Supplementary Table 2, recognition sequences and guide RNAs.
Rights and permissions
About this article
Cite this article
Cai, Y., Hossain, M.J., Hériché, JK. et al. Experimental and computational framework for a dynamic protein atlas of human cell division. Nature 561, 411–415 (2018). https://doi.org/10.1038/s41586-018-0518-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0518-z
Keywords
This article is cited by
-
A quantitative map of nuclear pore assembly reveals two distinct mechanisms
Nature (2023)
-
Structural landscape inside cells mapped in detail
Nature (2023)
-
Genetically encoded multimeric tags for subcellular protein localization in cryo-EM
Nature Methods (2023)
-
CasTuner is a degron and CRISPR/Cas-based toolkit for analog tuning of endogenous gene expression
Nature Communications (2023)
-
Digital entrepreneurship from cellular data: How omics afford the emergence of a new wave of digital ventures in health
Electronic Markets (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.