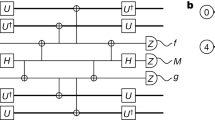
Abstract
A quantum computer has the potential to efficiently solve problems that are intractable for classical computers. However, constructing a large-scale quantum processor is challenging because of the errors and noise that are inherent in real-world quantum systems. One approach to addressing this challenge is to utilize modularity—a strategy used frequently in nature and engineering to build complex systems robustly. Such an approach manages complexity and uncertainty by assembling small, specialized components into a larger architecture. These considerations have motivated the development of a quantum modular architecture, in which separate quantum systems are connected into a quantum network via communication channels1,2. In this architecture, an essential tool for universal quantum computation is the teleportation of an entangling quantum gate3,4,5, but such teleportation has hitherto not been realized as a deterministic operation. Here we experimentally demonstrate the teleportation of a controlled-NOT (CNOT) gate, which we make deterministic by using real-time adaptive control. In addition, we take a crucial step towards implementing robust, error-correctable modules by enacting the gate between two logical qubits, encoding quantum information redundantly in the states of superconducting cavities6. By using such an error-correctable encoding, our teleported gate achieves a process fidelity of 79 per cent. Teleported gates have implications for fault-tolerant quantum computation3, and when realized within a network can have broad applications in quantum communication, metrology and simulations1,2,7. Our results illustrate a compelling approach for implementing multi-qubit operations on logical qubits and, if integrated with quantum error-correction protocols, indicate a promising path towards fault-tolerant quantum computation using a modular architecture.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability.
The data that support the findings of this study are available from the corresponding authors on reasonable request.
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Monroe, C. et al. Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 89, 022317 (2014).
Gottesman, D. & Chuang, I. L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 402, 390–393 (1999).
Eisert, J., Jacobs, K., Papadopoulos, P. & Plenio, M. B. Optimal local implementation of nonlocal quantum gates. Phys. Rev. A 62, 052317 (2000).
Jiang, L., Taylor, J. M., Sørensen, A. S. & Lukin, M. D. Distributed quantum computation based on small quantum registers. Phys. Rev. A 76, 062323 (2007).
Ofek, N. et al. Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 536, 441–445 (2016).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Ritter, S. et al. An elementary quantum network of single atoms in optical cavities. Nature 484, 195–200 (2012).
Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86–90 (2013).
Hucul, D. et al. Modular entanglement of atomic qubits using photons and phonons. Nat. Phys. 11, 37–42 (2015).
Narla, A. et al. Robust concurrent remote entanglement between two superconducting qubits. Phys. Rev. X 6, 031036 (2016).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993).
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997).
Furusawa, A. et al. Unconditional quantum teleportation. Science 282, 706–709 (1998).
Riebe, M. et al. Deterministic quantum teleportation with atoms. Nature 429, 734–737 (2004).
Barrett, M. D. et al. Deterministic quantum teleportation of atomic qubits. Nature 429, 737–739 (2004).
Sherson, J. F. et al. Quantum teleportation between light and matter. Nature 443, 557–560 (2006).
Olmschenk, S. et al. Quantum teleportation between distant matter qubits. Science 323, 486–489 (2009).
Steffen, L. et al. Deterministic quantum teleportation with feed-forward in a solid state system. Nature 500, 319–322 (2013).
Gottesman, D. The Heisenberg representation of quantum computers. Preprint at https://arxiv.org/abs/quant-ph/9807006 (1998).
Huang, Y.-F., Ren, X.-F., Zhang, Y.-S., Duan, L.-M. & Guo, G.-C. Experimental teleportation of a quantum controlled-NOT gate. Phys. Rev. Lett. 93, 240501 (2004).
Gao, W.-B. et al. Teleportation-based realization of an optical quantum two-qubit entangling gate. Proc. Natl Acad. Sci. USA 107, 20869–20874 (2010).
K., V. P., Joy, D., Behera, B. K. & Panigrahi, P. K. Experimental demonstration of non-local controlled- unitary quantum gates using a five-qubit quantum computer. Preprint at https://arxiv.org/abs/1709.05697 (2017).
Roch, N. et al. Observation of measurement-induced entanglement and quantum trajectories of remote superconducting qubits. Phys. Rev. Lett. 112, 170501 (2014).
Michael, M. H. et al. New class of quantum error-correcting codes for a bosonic mode. Phys. Rev. X 6, 031006 (2016).
Reagor, M. et al. Quantum memory with millisecond coherence in circuit QED. Phys. Rev. B 94, 014506 (2016).
Axline, C. et al. An architecture for integrating planar and 3D cQED devices. Appl. Phys. Lett. 109, 042601 (2016).
Paik, H. et al. Experimental Demonstration of a Resonator-Induced Phase Gate in a Multiqubit Circuit-QED System. Phys. Rev. Lett. 117, 250502 (2016).
Heeres, R. W. et al. Implementing a universal gate set on a logical qubit encoded in an oscillator. Nat. Commun. 8, 94 (2017).
Rosenblum, S. et al. A CNOT gate between multiphoton qubits encoded in two cavities. Nat. Commun. 9, 652 (2018).
Hann, C. T. et al. Robust readout of bosonic qubits in the dispersive coupling regime. Phys. Rev. A. 98, 022305 (2018).
Nickerson, N. H., Li, Y. & Benjamin, S. C. Topological quantum computing with a very noisy network and local error rates approaching one percent. Nat. Commun. 4, 1756 (2013).
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Barrett, S. D. & Kok, P. Efficient high-fidelity quantum computation using matter qubits and linear optics. Phys. Rev. A 71, 060310 (2005).
Bennett, C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722–725 (1996).
Vlastakis, B. et al. Deterministically encoding quantum information using 100-photon Schrödinger cat states. Science 342, 607–610 (2013).
Blumoff, J. Z. et al. Implementing and characterizing precise multiqubit measurements. Phys. Rev. X 6, 031041 (2016).
Chow, J. M. et al. Universal quantum gate set approaching fault-tolerant thresholds with superconducting qubits. Phys. Rev. Lett. 109, 060501 (2012).
Gilchrist, A., Langford, N. K. & Nielsen, M. A. Distance measures to compare real and ideal quantum processes. Phys. Rev. A 71, 062310 (2005).
Wootters, W. K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998).
Acknowledgements
We thank B. J. Lester, Z. K. Minev, A. Narla, U. Vool and I. L. Chuang for discussions on the manuscript, and A. Narla, K. Sliwa and N. Frattini for assistance on the parametric amplifier. Facilities use was supported by the Yale SEAS cleanroom, YINQE and NSF MRSEC DMR-1119826. This research was supported by the Army Research Office under grant numbers W911NF-14-1-0011 and W911NF-16-10349 and by the Air Force Office of Scientific Research under grant numbers FA9550-14-1-0052 and FA9550-15-1-0015. C.J.A. acknowledges support from a NSF Graduate Research Fellowship under grant number DGE-1122492. Y.Y.G. was supported by an A*STAR NSS Fellowship. L.J. acknowledges additional support from the Alfred P. Sloan Foundation under grant number BR2013-049 and from the Packard Foundation under grant number 2013-39273.
Author contributions
K.S.C., J.Z.B. and C.S.W. performed the experiment and analysed the data under the supervision of R.J.S. P.C.R. developed the feedforward control software and implemented the software used to generate optimal-control pulses. C.J.A., Y.Y.G. and L.F. fabricated the transmon qubits. K.S.C., J.Z.B. and R.J.S. designed the experiment. L.J., M.H.D. and L.F. provided theoretical support. K.S.C. and R.J.S. wrote the manuscript with contributions from all authors.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
R.J.S., M.H.D. and L.F. are founders, and R.J.S. and L.F. are equity shareholders, of Quantum Circuits, Inc.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Overview of the physical device.
a, Photograph of the full device assembly. The main body of the device is constructed from high-purity (99.99%) aluminium and contains four coaxial λ/4 three-dimensional cavities, three of which are used. The cavities that serve as the data qubits and the bus are outlined in magenta and purple, respectively. A detailed photograph of the cavities is shown in b. Two clamps anchor each sapphire chip; one is highlighted in cyan and detailed in c. The visible connectors are input ports for each cavity; the input and output ports for the transmon and readout resonators are on the underside of the device and therefore not visible. b, Top-down photograph of the cavities. We illustrate the three cavities using the same colour scheme as in a; the inner circle represents the inner conductor that defines the cavity mode; the cyan outline shows the sapphire chip inserted into the device package. Also visible are the antenna pads of the transmon that enable coupling to each cavity. c, Photograph of the sapphire chip on which the transmon and readout resonators are fabricated. The sapphire chip is outlined in cyan and contains several elements: from the top of the figure moving down, the Y-shaped transmon qubit, the readout resonator and the Purcell filter.
Extended Data Fig. 2 Assessing the independence of communication-qubit measurements.
a, Rabi experiment pulse sequence to extract measurement crosstalk. After initializing both communication qubits in the ground state, both qubits are rotated by \(\hat{X}\) rotations, with independent angles θ1 and θ2 for C1 and C2, respectively. Subsequently, measurements are performed on modules 1 and 2 and the result is recorded. b, c, Measurement crosstalk experimental results. For b (c), C2 (C1) is kept in the ground state, and a Rabi experiment is performed on C1 (C2). The measurement results are shown for C1 (green circles) and C2 (orange squares). For clarity, we describe the results focusing on b; the discussion is the same for c, save for swapping C1 and C2. Top, the C1 measurement results illustrate high-contrast oscillations, whereas the C2 measurement results remain close to zero, as expected when the communication-qubit measurements are independent. Bottom, close-up for measurement results on C2. The lack of structure in the data indicates that the measurement of C2 does not infer any information about the state of C1. To estimate the measurement crosstalk, we perform sinusoidal fits to the data by fixing the frequency and phase of the oscillation and extracting an amplitude and offset. Each data point in this experiment corresponds to 25,000 experiments. For data in the top panels, error bars are much smaller than the marker; for data in the bottom panels, we represent a typical error bar to be within the spread of the points. The slightly reduced contrast in c is specific to this calibration experiment, and potentially due to drifts in the transmon relaxation rate during the many hours of acquisition.
Extended Data Fig. 3 Implementation of the teleported CNOT gate.
a, Detailed circuit diagram for the teleported CNOT gate protocol. Top, pulse sequence for an example experiment. Bottom, legend for specific circuit blocks. In the first panel, we show our sequence for encoding quantum information onto the data qubit. In the second panel, we illustrate our implementation of the teleported CNOT gate. We show the pulse sequence used to generate the communication-qubit Bell state. For the communication-qubit measurements, we apply a π/2 rotation on C2 to measure \(\hat{X}\). After the measurement we also perform a measurement-based reset of C1 and C2 before performing feedforward operations on the data qubits. In the third panel, we detail two possible sequences for extracting the data-qubit state. For module 1, we perform logical tomography on the data qubits by decoding the data qubit onto the communication qubit and performing the appropriate tomography rotations on the communication qubit. For module 2, we perform Wigner tomography by performing a parity-mapping sequence on the communication qubit. b, Teleported CNOT gate timing diagram. The teleported CNOT gate is illustrated taking the relative timing of each element into account. The diagram is colour-coded with the following designations: black, single communication-qubit rotations; green, encode and decode (optimal control) operations; blue, teleported CNOT gate local operations (also optimal control); orange, measurements. This presentation provides a visual representation of the relative durations of each part of the protocol. Our implementation of the teleported CNOT gate takes a total of approximately 4.6 μs.
Extended Data Fig. 4 Communication-qubit Bell state.
a, Pulse sequence for generating the communication-qubit Bell pair. After generating the Bell state (first block), quantum state tomography is performed on both of the qubits to assess the quality of the entangled state. b, Characterizing the communication-qubit Bell pair. Experimentally measured Pauli vector components of the two communication qubits are shown. The generated state is \((| ge\rangle +| eg\rangle )/2\), with the ideal values denoted as hollow bars.
Extended Data Fig. 5 Communication-qubit measurement and reset.
a, Pulse sequence for testing communication-qubit measurement and reset. The two communication qubits (transmons) are initialized in the joint state \((| gg\rangle +| ge\rangle +| eg\rangle +| ee\rangle )/2\). The two qubits are then measured and if the measurement indicates that the state is projected to \(| e\rangle \) a π-pulse is applied to flip the state to the ground state. Conditional quantum state tomography is performed to analyse the quality of measurement and reset. This measurement and reset protocol is used in the teleported gate. b, Experimentally measured Pauli vector components conditioned on the measurement outcome. We assign a ‘0’ (‘1’) to indicate that the measurement projected the qubit to be in \(| g\rangle \) \(\left(| e\rangle \right)\). For all outcomes, we find high fidelity to the two-qubit ground state \(| gg\rangle \), as expected, with ground-state fidelities of {00, 99.3%; 01, 95.7%; 10, 97.7%; 11, 94.2%}. From these results, we establish that the measurement and feedback processes for each qubit are independent; from the single-qubit reset infidelities, we expect a measurement fidelity of 1 − (0.993 − 0.957) − (0.993 − 0.977) = 0.948, which is consistent with the result for measurement outcome 11. c, Experimentally measured state after measurement-based reset. Measurement results from b are combined, and the compiled results illustrate that the reset protocol is high-fidelity and independent of the measurement outcome. The fidelity of this reconstructed two-qubit state to \(| gg\rangle \) is 96.9%.
Extended Data Fig. 6 Extended binomial QPT data.
For each panel, we plot the process matrix in the Pauli transfer representation (bottom) and a reconstructed state represented in the Pauli basis (top). For the reconstructed state, we choose the input state \((| 0\rangle +| 1\rangle )| 0\rangle /\sqrt{2}\), which should result in the Bell state \(| {\Phi }^{+}\rangle =(| 00\rangle +| 11\rangle )/\sqrt{2}\) when the CNOT gate is applied. The ideal process for each panel is represented by the dominant components taken to ±1 and small components taken to 0. a, Conditioned QPT results when the feedforward operations are not applied. The first four panels (labelled ‘00’, ‘01’, ‘10’ and ‘11’) represent the processes conditioned on measurement outcome. Each has qualitatively the same features (for example, the same non-zero elements of the process matrix); however, the differing signs between the four outcomes indicate that each process is modified by single-qubit operations. When all measurement results are combined (labelled ‘All’), most of the features are washed away and only certain Pauli operators are left invariant by the process: {II, IX, ZI, ZX}. These operators are exactly the feedforward operations that would normally be applied. This behaviour can also be observed in the state tomography results (top), in which each measurement outcome heralds a different Bell state (\(\{| {\Psi }^{+}\rangle ,| {\Psi }^{-}\rangle ,| {\Phi }^{+}\rangle ,| {\Phi }^{-}\rangle \}\)); when taken all together, the states add incoherently, resulting in a completely mixed state. b, Conditioned QPT results when the feedforward operations are applied. Here, all measurement outcomes (00, 01, 10, 11) indicate the same process, that of the CNOT process. Therefore, when the measurement outcomes are all taken together (All), the compiled process is that of a CNOT gate.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data including Supplementary Methods, additional references, Supplementary Tables 1-5 and Supplementary Figures 1-8.
Rights and permissions
About this article
Cite this article
Chou, K.S., Blumoff, J.Z., Wang, C.S. et al. Deterministic teleportation of a quantum gate between two logical qubits. Nature 561, 368–373 (2018). https://doi.org/10.1038/s41586-018-0470-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0470-y
Keywords
This article is cited by
-
Protecting entanglement between logical qubits via quantum error correction
Nature Physics (2024)
-
Short-Distance Bidirectional Teleportation for Arbitrary Unknown Single-Qutrit States in Noise Environment
International Journal of Theoretical Physics (2024)
-
Realizing a deep reinforcement learning agent for real-time quantum feedback
Nature Communications (2023)
-
Beating the break-even point with a discrete-variable-encoded logical qubit
Nature (2023)
-
Progress in quantum teleportation
Nature Reviews Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.