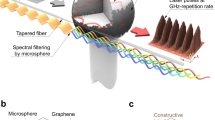
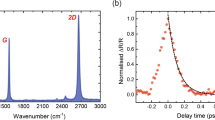
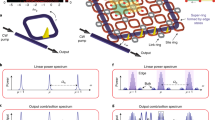
Abstract
Optical frequency combs, which emit pulses of light at discrete, equally spaced frequencies, are cornerstones of modern-day frequency metrology, precision spectroscopy, astronomical observations, ultrafast optics and quantum information1,2,3,4,5,6,7. Chip-scale frequency combs, based on the Kerr and Raman nonlinearities in monolithic microresonators with ultrahigh quality factors8,9,10, have recently led to progress in optical clockwork and observations of temporal cavity solitons11,12,13,14. But the chromatic dispersion within a laser cavity, which determines the comb formation15,16, is usually difficult to tune with an electric field, whether in microcavities or fibre cavities. Such electrically dynamic control could bridge optical frequency combs and optoelectronics, enabling diverse comb outputs in one resonator with fast and convenient tunability. Arising from its exceptional Fermi–Dirac tunability and ultrafast carrier mobility17,18,19, graphene has a complex optical dispersion determined by its optical conductivity, which can be tuned through a gate voltage20,21. This has brought about optoelectronic advances such as modulators22,23, photodetectors24 and controllable plasmonics25,26. Here we demonstrate the gated intracavity tunability of graphene-based optical frequency combs, by coupling the gate-tunable optical conductivity to a silicon nitride photonic microresonator, thus modulating its second- and higher-order chromatic dispersions by altering the Fermi level. Preserving cavity quality factors up to 106 in the graphene-based comb, we implement a dual-layer ion-gel-gated transistor to tune the Fermi level of graphene across the range 0.45–0.65 electronvolts, under single-volt-level control. We use this to produce charge-tunable primary comb lines from 2.3 terahertz to 7.2 terahertz, coherent Kerr frequency combs, controllable Cherenkov radiation and controllable soliton states, all in a single microcavity. We further demonstrate voltage-tunable transitions from periodic soliton crystals to crystals with defects, mapped by our ultrafast second-harmonic optical autocorrelation. This heterogeneous graphene microcavity, which combines single-atomic-layer nanoscience and ultrafast optoelectronics, will help to improve our understanding of dynamical frequency combs and ultrafast optics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Udem, T., Holzwarth, R. & Hansch, T. Optical frequency metrology. Nature 416, 233–237 (2002).
Kippenberg, T., Holzwarth, R. & Diddams, S. Microresonator-based optical frequency combs. Science 332, 555–559 (2011).
Cingöz, A. et al. Direct frequency comb spectroscopy in the extreme ultraviolet. Nature 482, 68–71 (2012).
Ideguchi, T. et al. Coherent Raman spectro-imaging using laser frequency combs. Nature 502, 355–358 (2013).
Steinmetz, T. et al. Laser frequency combs for astronomical observations. Science 321, 1335–1337 (2008).
Huang, S.-W. et al. Mode-locked ultrashort pulse generation from on-chip normal dispersion microresonators. Phys. Rev. Lett. 114, 053901 (2015).
Saglamyurek, E. et al. Broadband waveguide quantum memory for entangled photons. Nature 469, 512–515 (2011).
Del’Haye, P. et al. Optical frequency comb generation from a monolithic microresonator. Nature 450, 1214–1217 (2007).
Moss, D. J., Morandotti, R., Gaeta, A. L. & Lipson, M. New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics. Nat. Photon. 7, 597–607 (2013).
Yang, Q. F., Yi, X., Yang, K. Y. & Vahala, K. Stokes solitons in optical microcavities. Nat. Phys. 13, 53–57 (2016).
Xue, X. et al. Mode-locked dark pulse Kerr combs in normal-dispersion microresonators. Nat. Photon. 9, 594–600 (2015).
Huang, S.-W. et al. A broadband chip-scale optical frequency synthesizer at 2.7×10−16 relative uncertainty. Sci. Adv. 2, e1501489 (2016).
Brasch, V. et al. Photonic chip–based optical frequency comb using soliton Cherenkov radiation. Science 351, 357–360 (2016).
Marin-Palomo, P. et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 546, 274–279 (2017).
Del’Haye, P. et al. Phase-coherent microwave-to-optical link with a self-referenced microcomb. Nat. Photon. 10, 516–520 (2016).
Herr, T., Brasch, V., Jost, J., Wang, C. & Kondratiev, N. Temporal solitons in optical microresonators. Nat. Photon. 8, 145–152 (2014).
Wang, F. et al. Gate-variable optical transitions in graphene. Science 320, 206–209 (2008).
Li, Z., Henriksen, E., Jiang, Z., Hao, Z. & Martin, M. Dirac charge dynamics in graphene by infrared spectroscopy. Nat. Phys. 4, 532–535 (2008).
Bonaccorso, F., Sun, Z., Hasan, T. & Ferrari, A. Graphene photonics and optoelectronics. Nat. Photon. 4, 611–622 (2010).
Vakil, A. & Engheta, N. Transformation optics using graphene. Science 332, 1291–1294 (2011).
Gu, T. et al. Regenerative oscillation and four-wave mixing in graphene optoelectronics. Nat. Photon. 6, 554–559 (2012).
Liu, M. et al. A graphene-based broadband optical modulator. Nature 474, 64–67 (2011).
Phare, C., Lee, Y., Cardenas, J. & Lipson, M. Graphene electro-optic modulator with 30 GHz bandwidth. Nat. Photon. 9, 511–514 (2015).
Koppens, F. et al. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotech. 9, 780–793 (2014).
Grigorenko, A., Polini, M. & Novoselov, K. Graphene plasmonics. Nat. Photon. 6, 749–758 (2012).
Chakraborty, S. et al. Gain modulation by graphene plasmons in aperiodic lattice lasers. Science 351, 246–248 (2016).
Xu, Y. et al. Holey graphene frameworks for highly efficient capacitive energy storage. Nat. Commun. 5, 4554 (2014).
Das, A. et al. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotech. 3, 210–215 (2008).
Javerzac-Galy, C. et al. Excitonic emission of monolayer semiconductors near-field coupled to high-Q microresonators. Nano Lett. 18, 3138–3146 (2018).
Sorianello, V. et al. Graphene phase modulator. Nat. Photon. 12, 40–44 (2018).
Huang, S. et al. Globally stable microresonator Turing pattern formation for coherent high-power THz radiation on-chip. Phys. Rev. X 7, 041002 (2017).
Cole, D., Lamb, E., Del’Haye, P., Diddams, S. A. & Papp, S. B. Soliton crystals in Kerr resonators. Nat. Photon. 11, 671–676 (2017).
Acknowledgements
We thank J. Yang, B. Li, T. Itoh, H. Liu and X. Xie for discussions. Graphene fabrication was supported by the Nanoelectronics Research Facilities (NRF) of UCLA. The authors acknowledge support from the National Science Foundation (NSF; DMR-1611598, CBET-1520949 and EFRI-1741707), the University of California National Laboratory research program (LFRP-17-477237), the Office of Naval Research (N00014-16-1-2094) and the Air Force Office of Scientific Research (FA9550-15-1-0081). X.F.D. acknowledges support from the Office of Naval Research (N00014-15-1-2368) and Y.H. acknowledges support from the NSF (EFRI-1433541). This work is also supported by the National Science Foundation of China (61705032) and the 111 project of China (B14039).
Reviewer information
Nature thanks T. Tanabe and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
B.Y. and S.-W.H. designed and led the work on the graphene–nitride frequency combs including the first and detailed measurements, the gate-tuned ultrafast optics measurements and the numerical designs. Y.L. and Z.Y.F. performed the graphene–nitride integration, conducted relevant electrical measurements and device optimizations. B.Y., C.C., S.-W.H., M.H., M.Y. and D.-L.K. performed silicon nitride chip and device processing. Y.H. and X.F.D. supervised graphene material preparation, device fabrication and electronic measurements. B.Y., A.K.V., S.-W.H. and C.W.W. performed the measured data analysis, on the frequency comb, radiofrequency and ultrafast correlation measurements. S.-W.H., B.Y. and Y.N.L. provided the theory and numerical calculations. All authors discussed the results. B.Y., S.-W.H., Y.L., Y.J.R. and C.W.W. prepared the manuscript. C.W.W. led and supported this research.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Measured gate-tunable coupling and dispersions in a GMR.
a, Dips at approximately 1,600 nm, with different VG. b, Correlation of the round-trip transmissions and the bus transmissions for the resonator, obeying T = (α−|t|)2/(α−α|t|)2. Here, 1−α is the cavity loss per round trip, and 1−t is the bus-to-cavity coupling rate. In our experiment, the graphene ring resonator is under-coupled originally, as the blue dot shows. c, Group velocity dispersion in range of 1,500 nm to 1,700 nm. Here, the curves show the calculated results, while dots show measured data. d, Calculated third-order dispersion in range of 1,500 nm to 1,700 nm.
Extended Data Fig. 2 Comparative optical transmissions of the heterogeneous graphene–nitride ring.
a, Spectral transmission of the silicon nitride ring resonator under the silica overcladding. b, Spectral transmission of the silicon nitride ring resonator after buffer-oxide etching to remove the silica overcladding. c, Spectral transmission of the graphene/ion-gel-based nitride ring resonator, heavily p-doped (VG = −2 V). d, Loaded Q factor around 1,600 nm. e, FSR, which is sensitive to the geometry modification. f, Mode non-equidistances, D2. d and e are measured at λ = 1,600 nm. In this figure, the error bars denote the typical system error.
Extended Data Fig. 3 An implementation of the graphene primary frequency comb gate-modulation.
a, Method for measuring the modulated comb. Keeping bias VG = −1.2 V, we control the laser-cavity detuning to generate a primary comb such as the grey spectrum shown here. To filter off the 1,600-nm continuous-wave pump, we apply a C-band filter, selecting the comb lines in the C-band only. A signal generator (maximum amplitude of 2 V, HP3312) is applied to modulate the gate voltage between −1.2 V and −1.8 V. In this process, primary comb lines in the filter window are modulated by the gate signal; the modulation is monitored by using an oscilloscope (500 MHz, Rigol DS1054) and an electrical spectrum analyser (ESA, 3 GHz, Agilent CXA9000A). b, Examples of radiofrequency spectra of the modulated combs, filtered by an optical filter (1,530 nm to 1,570 nm).
Extended Data Fig. 4 Example measurements of the graphene soliton comb formation.
a, Under VG = −1.2 V (Fermi level 0.59 eV), when the wavelength of the pump (λp) is tuned from 1,600.00 nm to 1,600.23 nm, the Kerr frequency comb is generated gradually. When λp is tuned between 1,600.15 nm and 1,600.19 nm, two multi-soliton states with low phase noise are achieved (states iv and v). b, Corresponding radiofrequency (RF) amplitude noise of the six states. In a and b, the pump power is kept at 34.5 dBm. Cherenkov radiation of the multi-soliton comb is narrow and sharp. c, Zoom-in of the eight-soliton crystal spectrum. The FSR changes from 89 GHz to 718 GHz, owing to the soliton-crystal-based longitude mode interaction. d, Beat note for the comb lines of the eight-soliton state (red; ninth comb line offset from the pump) and the four-soliton state (green; 56th comb line offset from the pump).
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary Figures 1-16 and Supplementary References.
Rights and permissions
About this article
Cite this article
Yao, B., Huang, SW., Liu, Y. et al. Gate-tunable frequency combs in graphene–nitride microresonators. Nature 558, 410–414 (2018). https://doi.org/10.1038/s41586-018-0216-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0216-x
This article is cited by
-
A Review of a Spectral Domain Interferometer with a Frequency Comb for Length Measurement
International Journal of Precision Engineering and Manufacturing (2024)
-
Photonic van der Waals integration from 2D materials to 3D nanomembranes
Nature Reviews Materials (2023)
-
Versatile tuning of Kerr soliton microcombs in crystalline microresonators
Communications Physics (2023)
-
Graphene oxide for photonics, electronics and optoelectronics
Nature Reviews Chemistry (2023)
-
Near-zero-dispersion soliton and broadband modulational instability Kerr microcombs in anomalous dispersion
Light: Science & Applications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.