Abstract
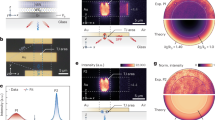
Graphene, a single-layer network of carbon atoms, has outstanding electrical and mechanical properties1. Graphene ribbons with nanometre-scale widths2,3 (nanoribbons) should exhibit half-metallicity4 and quantum confinement. Magnetic edges in graphene nanoribbons5,6 have been studied extensively from a theoretical standpoint because their coherent manipulation would be a milestone for spintronic7 and quantum computing devices8. However, experimental investigations have been hampered because nanoribbon edges cannot be produced with atomic precision and the graphene terminations that have been proposed are chemically unstable9. Here we address both of these problems, by using molecular graphene nanoribbons functionalized with stable spin-bearing radical groups. We observe the predicted delocalized magnetic edge states and test theoretical models of the spin dynamics and spin–environment interactions. Comparison with a non-graphitized reference material enables us to clearly identify the characteristic behaviour of the radical-functionalized graphene nanoribbons. We quantify the parameters of spin–orbit coupling, define the interaction patterns and determine the spin decoherence channels. Even without any optimization, the spin coherence time is in the range of microseconds at room temperature, and we perform quantum inversion operations between edge and radical spins. Our approach provides a way of testing the theory of magnetism in graphene nanoribbons experimentally. The coherence times that we observe open up encouraging prospects for the use of magnetic nanoribbons in quantum spintronic devices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
26 June 2018
In Fig. 1 of this Letter, there should have been two nitrogen (N) atoms at the 1,3-positions of all the blue chemical structures (next to the oxygen atoms), rather than one at the 2-position. The figure has been corrected online, and the original incorrect figure is shown as Supplementary Information to the accompanying Amendment.
References
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009).
Jiao, L., Zhang, L., Wang, X., Diankov, G. & Dai, H. Narrow graphene nanoribbons from carbon nanotubes. Nature 458, 877–880 (2009).
Jia, X. et al. Controlled formation of sharp zigzag and armchair edges in graphitic nanoribbons. Science 323, 1701–1705 (2009).
Son, Y. W., Cohen, M. L. & Louie, S. G. Half-metallic graphene nanoribbons. Nature 444, 347–349 (2006). corrigendum 446, 342 (2007).
Recher, P. & Trauzettel, B. Quantum dots and spin qubits in graphene. Nanotechnology 21, 302001 (2010).
Meunier, V., Souza Filho, A. G., Barros, E. B. & Dresselhaus, M. S. Physical properties of low-dimensional sp 2-based carbon nanostructures. Rev. Mod. Phys. 88, 025005 (2016).
Pesin, D. & MacDonald, A. H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mater. 11, 409–416 (2012).
Trauzettel, B., Bulaev, D. V., Loss, D. & Burkard, G. Spin qubits in graphene quantum dots. Nat. Phys. 3, 192–196 (2007).
Barone, V., Hod, O. & Scuseria, G. E. Electronic structure and stability of semiconducting graphene nanoribbons. Nano Lett. 6, 2748–2754 (2006).
Narita, A., Wang, X.-Y., Feng, X. & Müllen, K. New advances in nanographene chemistry. Chem. Soc. Rev. 44, 6616–6643 (2015).
Ruffieux, P. et al. On-surface synthesis of graphene nanoribbons with zigzag edge topology. Nature 531, 489–492 (2016).
Cai, J. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 466, 470–473 (2010).
Caneschi, A., Gatteschi, D. & Rey, P. The chemistry and magnetic properties of metal nitronyl nitroxide complexes. Prog. Inorg. Chem. 39, 331–429 (1991).
Collauto, A. et al. A slow relaxing species for molecular spin devices: EPR characterization of static and dynamic magnetic properties of a nitronyl nitroxide radical. J. Mater. Chem. 22, 22272–22281 (2012).
Narita, A. et al. Synthesis of structurally well-defined and liquid-phase-processable graphene nanoribbons. Nat. Chem. 6, 126–132 (2014).
Zheludev, A. et al. Spin-density in a nitronyl nitroxide free-radical-polarized neutron-diffraction investigation and ab initio calculations. J. Am. Chem. Soc. 116, 2019–2027 (1994).
Schweiger, A. & Jeschke, G. Principles of Pulse Electron Paramagnetic Resonance (Oxford Univ. Press, Oxford, 2001).
Golor, M., Wessel, S. & Schmidt, M. J. Quantum nature of edge magnetism in graphene. Phys. Rev. Lett. 112, 046601 (2014).
Rao, S. S. et al. Spin dynamics and relaxation in graphene nanoribbons: electron spin resonance probing. ACS Nano 6, 7615–7623 (2012).
Min, H. et al. Intrinsic and Rashba spin-orbit interactions in graphene sheets. Phys. Rev. B 74, 165310 (2006).
Kane, C. L. & Mele, E. J. Z 2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Eaton, G. R. & Eaton, S. S. in Multifrequency Electron Paramagnetic Resonance: Theory and Applications (ed. Misra, S. K.) Ch. 17 (Wiley, Weinheim, 2011).
Klauder, J. R. & Anderson, P. W. Spectral diffusion decay in spin resonance experiments. Phys. Rev. 125, 912–932 (1962).
Struck, P. R. & Burkard, G. Effective time-reversal symmetry breaking in the spin relaxation in a graphene quantum dot. Phys. Rev. B 82, 125401 (2010).
Drögeler, M. et al. Spin lifetimes exceeding 12 ns in graphene nonlocal spin valve devices. Nano Lett. 16, 3533–3539 (2016).
Fischer, J., Trauzettel, B. & Loss, D. Hyperfine interaction and electron-spin decoherence in graphene and carbon nanotube quantum dots. Phys. Rev. B 80, 155401 (2009).
Dutt, M. G. et al. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 316, 1312–1316 (2007).
Foletti, S., Bluhm, H., Mahalu, D., Umansky, V. & Yacoby, A. Universal quantum control of two-electron spin quantum bits using dynamic nuclear polarization. Nat. Phys. 5, 903–908 (2009).
Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 8, 383–387 (2009).
Shiddiq, M. et al. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 531, 348–351 (2016).
Narita, A. et al. Bottom-up synthesis of liquid-phase-processable graphene nanoribbons with near-infrared absorption. ACS Nano 8, 11622–11630 (2014).
Keerthi, A. et al. Hexa-peri-hexabenzocoronene with different acceptor units for tuning optoelectronic properties. Chem. Asian J. 11, 2710–2714 (2016).
Stoll, S. & Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 178, 42–55 (2006).
Wacker, T., Sierra, G. A. & Schweiger, A. The concept of FID-detected hole-burning in pulsed EPR spectroscopy. Isr. J. Chem. 32, 305–322 (1992).
Rintoul, L., Micallef, A. S. & Bottle, S. E. The vibrational group frequency of the N–O rad stretching band of nitroxide stable free radical. Spectrochim. Acta A 70, 713–717 (2008).
Cox, N., Lubitz, W. & Savitzky, A. W-band ELDOR-detected NMR (EDNMR) spectroscopy as a versatile technique for the characterisation of transition metal–ligand interactions. Mol. Phys. 111, 2788–2808 (2013).
Jeschke, G. et al. DeerAnalysis2006—a comprehensive software package for analyzing pulsed ELDOR data. Appl. Magn. Reson. 30, 473–498 (2006).
Gaussian 09. revision A.02. (Gaussian, Wallingford, 2016).
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 14, 2745–2779 (2002).
Acknowledgements
We thank the European Research Council (ERC-StG 338258 OptoQMol), the EU (COST-CA15128, MOLESCO-606728 and Graphene Flagship), the EPSRC (QuEEN grant), the Royal Society (University Research Fellowship and URF grant), the RFBR (17-53-50043), the Max Planck Society and the German DAAD Bilateral Exchange of Academics (2015/50015739) for financial support.
Reviewer information
Nature thanks E. Coronado, D. Gatteschi, A.-P. Li and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
M.S. and W.K.M. performed the ESR characterization. A.K. and E.T. performed the synthesis and related characterization, for which M.B., A.N. and K.M. provided supervision. H.S. and C.J.L. performed the numerical modelling. M.S., W.K.M., A.A. and L.B. contributed to the ESR data analysis. M.S., A.N., K.M. and L.B. conceived the experiments and M.S. and L.B. wrote the manuscript. All authors contributed to the discussion and to the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary Figures 1-15, Supplementary Tables 1-3 and a Supplementary Bibliography.
Rights and permissions
About this article
Cite this article
Slota, M., Keerthi, A., Myers, W.K. et al. Magnetic edge states and coherent manipulation of graphene nanoribbons. Nature 557, 691–695 (2018). https://doi.org/10.1038/s41586-018-0154-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0154-7
This article is cited by
-
Open-Shell Oligomers and Polymers: Theory, Characterization Methods, Molecular Design, and Applications
Chinese Journal of Polymer Science (2024)
-
A Stable Open-Shell Conjugated Diradical Polymer with Ultra-High Photothermal Conversion Efficiency for NIR-II Photo-Immunotherapy of Metastatic Tumor
Nano-Micro Letters (2024)
-
Detecting the spin-polarization of edge states in graphene nanoribbons
Nature Communications (2023)
-
Twisted bilayer zigzag-graphene nanoribbon junctions with tunable edge states
Nature Communications (2023)
-
Exceptionally clean single-electron transistors from solutions of molecular graphene nanoribbons
Nature Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.