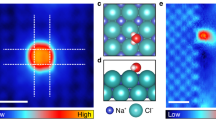
Abstract
Ion hydration and transport at interfaces are relevant to a wide range of applied fields and natural processes1,2,3,4,5. Interfacial effects are particularly profound in confined geometries such as nanometre-sized channels6,7,8, where the mechanisms of ion transport in bulk solutions may not apply9,10. To correlate atomic structure with the transport properties of hydrated ions, both the interfacial inhomogeneity and the complex competing interactions among ions, water and surfaces require detailed molecular-level characterization. Here we constructed individual sodium ion (Na+) hydrates on a NaCl(001) surface by progressively attaching single water molecules (one to five) to the Na+ ion using a combined scanning tunnelling microscopy and noncontact atomic force microscopy system. We found that the Na+ ion hydrated with three water molecules diffuses orders of magnitude more quickly than other ion hydrates. Ab initio calculations revealed that such high ion mobility arises from the existence of a metastable state, in which the three water molecules around the Na+ ion can rotate collectively with a rather small energy barrier. This scenario would apply even at room temperature according to our classical molecular dynamics simulations. Our work suggests that anomalously high diffusion rates for specific hydration numbers of ions are generally determined by the degree of symmetry match between the hydrates and the surface lattice.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
22 August 2018
In this Letter, the links to Supplementary Videos 5, 7, 9 and 10 were incorrect, and there were some formatting errors in the Supplementary Video legends. These errors have been corrected online.
References
Sipilä, M. et al. Molecular-scale evidence of aerosol particle formation via sequential addition of HIO3. Nature 537, 532–534 (2016).
Klimeš, J., Bowler, D. R. & Michaelides, A. Understanding the role of ions and water molecules in the NaCl dissolution process. J. Chem. Phys. 139, 234702 (2013).
Cohen-Tanugi, D. & Grossman, J. C. Water desalination across nanoporous graphene. Nano Lett. 12, 3602–3608 (2012).
Payandeh, J., Scheuer, T., Zheng, N. & Catterall, W. A. The crystal structure of a voltage-gated sodium channel. Nature 475, 353–358 (2011).
Gouaux, E. & MacKinnon, R. Principles of selective ion transport in channels and pumps. Science 310, 1461–1465 (2005).
Schoch, R. B., Han, J. & Renaud, P. Transport phenomena in nanofluidics. Rev. Mod. Phys. 80, 839–883 (2008).
Guo, W., Tian, Y. & Jiang, L. Asymmetric ion transport through ion-channel-mimetic solid-state nanopores. Acc. Chem. Res. 46, 2834–2846 (2013).
Whitby, M. & Quirke, N. Fluid flow in carbon nanotubes and nanopipes. Nat. Nanotechnol. 2, 87–94 (2007).
Stein, D., Kruithof, M. & Dekker, C. Surface-charge-governed ion transport in nanofluidic channels. Phys. Rev. Lett. 93, 035901 (2004).
Duan, C. & Majumdar, A. Anomalous ion transport in 2-nm hydrophilic nanochannels. Nat. Nanotechnol. 5, 848–852 (2010).
Omta, A. W., Kropman, M. F., Woutersen, S. & Bakker, H. J. Negligible effect of ions on the hydrogen-bond structure in liquid water. Science 301, 347–349 (2003).
Heisler, I. A. & Meech, S. R. Low-frequency modes of aqueous alkali halide solutions: glimpsing the hydrogen bonding vibration. Science 327, 857–860 (2010).
Tielrooij, K. J., Garcia-Araez, N., Bonn, M. & Bakker, H. J. Cooperativity in ion hydration. Science 328, 1006–1009 (2010).
Carrillo-Tripp, M., Saint-Martin, H. & Ortega-Blake, I. A comparative study of the hydration of Na+ and K+ with refined polarizable model potentials. J. Chem. Phys. 118, 7062 (2003).
Jungwirth, P. & Tobias, D. J. Specific ion effects at the air/water interface. Chem. Rev. 106, 1259–1281 (2006).
Kumagai, T. et al. H-atom relay reactions in real space. Nat. Mater. 11, 167–172 (2012).
Carrasco, J., Hodgson, A. & Michaelides, A. A molecular perspective of water at metal interfaces. Nat. Mater. 11, 667–674 (2012).
Guo, J. et al. Real-space imaging of interfacial water with submolecular resolution. Nat. Mater. 13, 184–189 (2014).
Maier, S. & Salmeron, M. How does water wet a surface? Acc. Chem. Res. 48, 2783–2790 (2015).
Shiotari, A. & Sugimoto, Y. Ultrahigh-resolution imaging of water networks by atomic force microscopy. Nat. Commun. 8, 14313 (2017).
Peng, J. et al. Weakly perturbative imaging of interfacial water with submolecular resolution by atomic force microscopy. Nat. Commun. 9, 122 (2018).
Meng, X. et al. Direct visualization of concerted proton tunnelling in a water nanocluster. Nat. Phys. 11, 235–239 (2015).
Fukuma, T., Ueda, Y., Yoshioka, S. & Asakawa, H. Atomic-scale distribution of water molecules at the mica–water interface visualized by three-dimensional scanning force microscopy. Phys. Rev. Lett. 104, 016101 (2010).
Ricci, M., Spijker, P. & Voitchovsky, K. Water-induced correlation between single ions imaged at the solid–liquid interface. Nat. Commun. 5, 4400 (2014).
Giessibl, F. J. Advances in atomic force microscopy. Rev. Mod. Phys. 75, 949–983 (2003).
Peng, J. et al. Atomic-scale imaging of the dissolution of NaCl islands by water at low temperature. J. Phys. Condens. Matter 29, 104001 (2017).
Gross, L. et al. The chemical structure of a molecule resolved by atomic force microscopy. Science 325, 1110–1114 (2009).
Gawronski, H., Carrasco, J., Michaelides, A. & Morgenstern, K. Manipulation and control of hydrogen bond dynamics in absorbed ice nanoclusters. Phys. Rev. Lett. 101, 136102 (2008).
Stipe, B. C., Rezaei, M. A. & Ho, W. Single-molecule vibrational spectroscopy and microscopy. Science 280, 1732–1735 (1998).
Fuentes-Azcatl, R. & Barbosa, M. C. Sodium chloride, NaCl/ε: new force field. J. Phys. Chem. B 120, 2460–2470 (2016).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Klimeš, J., Bowler, D. R. & Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 22, 022201 (2010).
Klimeš, J., Bowler, D. R. & Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011).
Neugebauer, J. & Scheffler, M. Adsorbate-substrate and adsorbate–adsorbate interactions of Na and K adlayers on Al(111). Phys. Rev. B 46, 16067–16080 (1992).
Makov, G. & Payne, M. C. Periodic boundary conditions in ab initio calculations. Phys. Rev. B 51, 4014–4022 (1995).
Henkelman, G., Arnaldsson, A. & Jonsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 36, 354–360 (2006).
Henkelman, G. & Jonsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 113, 9978–9985 (2000).
Henkelman, G., Uberuaga, B. P. & Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Hapala, P., Temirov, R., Tautz, F. S. & Jelinek, P. Origin of high-resolution IETS-STM images of organic molecules with functionalized tips. Phys. Rev. Lett. 113, 226101 (2014).
Hapala, P. et al. Mechanism of high-resolution STM/AFM imaging with functionalized tips. Phys. Rev. B 90, 085421 (2014).
Ellner, M. et al. The electric field of CO tips and its relevance for atomic force microscopy. Nano Lett. 16, 1974–1980 (2016).
Leontyev, I. V. & Stuchebrukhov, A. A. Polarizable molecular interactions in condensed phase and their equivalent nonpolarizable models. J. Chem. Phys. 141, 014103 (2014).
Hansen, J. P. & McDonald, I. R. Theory of Simple Liquids 3rd edn (Academic Press, 2006).
Berendsen, H. J. C., Grigera, J. R. & Straatsma, T. P. The missing term in effective pair potentials. J. Phys. Chem. 91, 6269–6271 (1987).
Joung, I. S. & Cheatham, T. E. Molecular dynamics simulations of the dynamic and energetic properties of alkali and halide ions using water-model-specific ion parameters. J. Phys. Chem. B 113, 13279–13290 (2009).
Case, D. A. et al. AMBER version 14. http://ambermd.org (University of California, San Francisco, 2014).
Ryckaert, J. P., Ciccotti, G. & Berendsen, H. J. C. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23, 327–341 (1977).
Acknowledgements
This work was supported by the National Key R&D Program under grant numbers 2016YFA0300901, 2017YFA0205003, 2016YFA0300903 and 2015CB856801; the National Natural Science Foundation of China under grant numbers 11634001, 11525520, 21573006 and 11290162/A040106; and the Key Research Program of the Chinese Academy of Sciences under grant numbers XDPB08-1 and XDPB08-4. Y.J. acknowledges support by the National Science Fund for Distinguished Young Scholars (grant number 21725302) and the Cheung Kong Young Scholar Program. P.H. and P.J. acknowledge support from the Czech Academy of Sciences project number MSM100101705 and Premium Academiae and GACR project number 18-09914S. J.G. acknowledges support from the National Postdoctoral Program for Innovative Talents. J.P. acknowledges support from the Weng Hongwu Original Research Foundation under grant number WHW201502. We are grateful for the computational resources provided by the TianHe-1A, TianHe II supercomputer, and the High-performance Computing Platform of Peking University. This work is supported in part by Songshan Lake Laboratory for Material Sciences.
Reviewer information
Nature thanks P. Asinari and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
Y.J. and E.-G.W. designed and supervised the project. J.P. performed the STM/AFM measurements (with J.G. and R.M.). D.C., J.C., X.-Z.L. and L.-M.X. performed ab initio DFT calculations. Z.H., W.J.X. and Y.Q.G. carried out the classical molecular dynamics simulations. P.H. and P.J. carried out the theoretical simulations of the AFM images (in collaboration with D.C. and B.C.). J.P., D.C., Z.H., J.G., W.J.X., X.-Z.L., Y.Q.G., L.-M.X., E.-G.W. and Y.J. analysed the data. Y.J. wrote the manuscript with input from all other authors. The manuscript reflects the contributions of all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Text 1–13 (see contents page for more details), Supplementary Figures S1–S13, Supplementary Tables S1–S3 and references.
Video 1: Diffusion trajectory of Na+⋅H2O on NaCl(001) surface during a period of 10 ns.
The video was generated by molecular dynamics simulations at 275 K. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. Overall diffusion dynamics can be seen clearly in the video.
Video 2: Diffusion trajectory of Na+⋅2H2O on NaCl(001) surface during a period of 10 ns.
The video was generated by molecular dynamics simulations at 275 K. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. Overall diffusion dynamics can be seen clearly in the video.
Video 3: Diffusion trajectory of Na+⋅3H2O on NaCl(001) surface during a period of 10 ns.
The video was generated by molecular dynamics simulations at 275 K. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. Overall diffusion dynamics can be seen clearly in the video. The mobility of Na+·3H2O is more than one order of magnitude larger than that of other clusters.
Video 4: Diffusion trajectory of Na+⋅4H2O on NaCl(001) surface during a period of 10 ns.
The video was generated by molecular dynamics simulations at 275 K. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. Overall diffusion dynamics can be seen clearly in the video.
Video 5: Diffusion trajectory of Na+⋅5H2O on NaCl(001) surface during a period of 10 ns.
The video was generated by molecular dynamics simulations at 275 K. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. Overall diffusion dynamics can be seen clearly in the video.
Video 6: Diffusion trajectory of Na+⋅H2O during a period of 20 ps.
The video was generated by molecular dynamics simulations at 300 K and played with a 2,000-times higher frame rate than Supplementary Video 1. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. The intermediate transitions during the diffusion can be seen clearly in the video. Na·H2O hops between the bridge sites, accompanied with the rotation of water around the Na+.
Video 7: Diffusion trajectory of Na+⋅2H2O during a period of 20 ps.
The video was generated by molecular dynamics simulations at 300 K and played with a 2,000-times higher frame rate than Supplementary Video 2. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. Na+·2H2O hops between the bridge sites, accompanied with the rotation of two water molecules around the Na+.
Video 8: Diffusion trajectory of Na+⋅3H2O during a period of 20 ps.
The video was generated by molecular dynamics simulations at 300 K and played with a 2,000-times higher frame rate than Supplementary Video 3. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. The diffusion of Na+·3H2O is facilitated by a metastable state (Fig. 4f), where the Na+ is located at the top Cl− site of NaCl in contrast to the bridge site in the most stable state (Fig. 4e). See Fig. 4 for detailed discussions.
Video 9: Diffusion trajectory of Na+⋅4H2O during a period of 20 ps.
The video was generated by molecular dynamics simulations at 300 K and played with a 2,000-times higher frame rate than Supplementary Video 4. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. Na+·4H2O hops between the top Cl− sites. The diffusion of Na+·4H2O is usually accompanied with the flipping of water molecules, that is, one water molecule climbs onto the top of the Na+ ion, leaving the rest three in contact with the surface. Such a configuration resembles that of Na+·3H2O, leading to the stabilization at the bridge site. See Supplementary Figure 11 for detailed discussions.
Video 10: Diffusion trajectory of Na+⋅5H2O during a period of 20 ps.
The video was generated by molecular dynamics simulations at 300 K and played with a 2,000-times higher frame rate than Supplementary Video 5. H, O, Cl, Na atoms are denoted as white, red, green and purple spheres, respectively. Na+·5H2O hops between the top Cl− sites and shows a similar flipping-assisted diffusion behaviour to Na+·4H2O. See Supplementary Figure 11 for detailed discussions.
Rights and permissions
About this article
Cite this article
Peng, J., Cao, D., He, Z. et al. The effect of hydration number on the interfacial transport of sodium ions. Nature 557, 701–705 (2018). https://doi.org/10.1038/s41586-018-0122-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0122-2
This article is cited by
-
Keto-anthraquinone covalent organic framework for H2O2 photosynthesis with oxygen and alkaline water
Nature Communications (2024)
-
Nanoscale one-dimensional close packing of interfacial alkali ions driven by water-mediated attraction
Nature Nanotechnology (2024)
-
Impact of hierarchical water dipole orderings on the dynamics of aqueous salt solutions
Nature Communications (2023)
-
Constructing two-dimensional interfacial ice-like water at room temperature for nanotribology
Nano Research (2023)
-
Atomic-scale visualization of chiral charge density wave superlattices and their reversible switching
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.