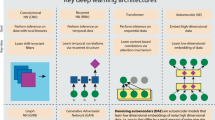
Abstract
As a data-driven science, genomics largely utilizes machine learning to capture dependencies in data and derive novel biological hypotheses. However, the ability to extract new insights from the exponentially increasing volume of genomics data requires more expressive machine learning models. By effectively leveraging large data sets, deep learning has transformed fields such as computer vision and natural language processing. Now, it is becoming the method of choice for many genomics modelling tasks, including predicting the impact of genetic variation on gene regulatory mechanisms such as DNA accessibility and splicing.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$189.00 per year
only $15.75 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
References
Hieter, P. & Boguski, M. Functional genomics: it’s all how you read it. Science 278, 601–602 (1997).
Brown, P. O. & Botstein, D. Exploring the new world of the genome with DNA microarrays. Nat. Genet. 21, 33–37 (1999).
Ozaki, K. et al. Functional SNPs in the lymphotoxin-α gene that are associated with susceptibility to myocardial infarction. Nat. Genet. 32, 650–654 (2002).
Golub, T. R. et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286, 531–537 (1999).
Oliver, S. Guilt-by-association goes global. Nature 403, 601–603 (2000).
The ENCODE Project Consortium. An integrated encyclopedia of DNA elements in the human genome. Nature 489, 57–74 (2012).
Murphy, K. P. Machine Learning: A Probabilistic Perspective (MIT Press, 2012).
Bishop, C. M. Pattern Recognition and Machine Learning (Springer, New York, 2016).
Libbrecht, M. W. & Noble, W. S. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 16, 321–332 (2015).
Durbin, R., Eddy, S. R., Krogh, A. & Mitchison, G. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids (Cambridge Univ. Press, 1998).
Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning (MIT Press, 2016). This textbook covers theoretical and practical aspects of deep learning with introductory sections on linear algebra and machine learning.
Shi, S., Wang, Q., Xu, P. & Chu, X. in 2016 7th International Conference on Cloud Computing and Big Data (CCBD) 99–104 (IEEE, 2016).
Krizhevsky, A., Sutskever, I. & Hinton, G. E. in Advances in Neural Information Processing Systems 25 (NIPS 2012) (eds Pereira, F., Burges, C. J. C., Bottou, L. & Weinberger, K. Q.) 1097–1105 (Curran Associates, Inc., 2012).
Girshick, R., Donahue, J., Darrell, T. & Malik, J. in 2014 IEEE Conference on Computer Vision and Pattern Recognition 580–587 (IEEE, 2014).
Long, J., Shelhamer, E. & Darrell, T. in 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 3431–3440 (IEEE, 2015).
Hannun, A. et al. Deep speech: scaling up end-to-end speech recognition. Preprint at arXiv https://arxiv.org/abs/1412.5567 (2014).
Wu, Y. et al. Google’s neural machine translation system: bridging the gap between human and machine translation. Preprint at arXiv https://arxiv.org/abs/1609.08144 (2016).
Alipanahi, B., Delong, A., Weirauch, M. T. & Frey, B. J. Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat. Biotechnol. 33, 831–838 (2015). This paper describes a pioneering convolutional neural network application in genomics.
Zhou, J. & Troyanskaya, O. G. Predicting effects of noncoding variants with deep learning-based sequence model. Nat. Methods 12, 931–934 (2015). This paper applies deep CNNs to predict chromatin features and transcription factor binding from DNA sequence and demonstrates its utility in non-coding variant effect prediction.
Zou, J. et al. A primer on deep learning in genomics. Nat. Genet. 51, 12–18 (2019).
Angermueller, C., Pärnamaa, T., Parts, L. & Stegle, O. Deep learning for computational biology. Mol. Syst. Biol. 12, 878 (2016).
Min, S., Lee, B. & Yoon, S. Deep learning in bioinformatics. Brief. Bioinform. 18, 851–869 (2017).
Jones, W., Alasoo, K., Fishman, D. & Parts, L. Computational biology: deep learning. Emerg. Top. Life Sci. 1, 257–274 (2017).
Wainberg, M., Merico, D., Delong, A. & Frey, B. J. Deep learning in biomedicine. Nat. Biotechnol. 36, 829–838 (2018).
Ching, T. et al. Opportunities and obstacles for deep learning in biology and medicine. J. R. Soc. Interface 15, 20170387 (2018).
Morgan, J. N. & Sonquist, J. A. Problems in the analysis of survey data, and a proposal. J. Am. Stat. Assoc. 58, 415–434 (1963).
Boser, B. E., Guyon, I. M. & Vapnik, V. N. A. in Proceedings of the Fifth Annual Workshop on Computational Learning Theory 144–152 (ACM, 1992).
Breiman, L. Random forests. Mach. Learn. 45, 5–32 (2001).
Friedman, J. H. Greedy function approximation: a gradient boosting machine. Ann. Stat. 29, 1189–1232 (2001).
Xiong, H. Y. et al. RNA splicing. The human splicing code reveals new insights into the genetic determinants of disease. Science 347, 1254806 (2015).
Jha, A., Gazzara, M. R. & Barash, Y. Integrative deep models for alternative splicing. Bioinformatics 33, i274–i282 (2017).
Quang, D., Chen, Y. & Xie, X. DANN: a deep learning approach for annotating the pathogenicity of genetic variants. Bioinformatics 31, 761–763 (2015).
Liu, F., Li, H., Ren, C., Bo, X. & Shu, W. PEDLA: predicting enhancers with a deep learning-based algorithmic framework. Sci. Rep. 6, 28517 (2016).
Li, Y., Shi, W. & Wasserman, W. W. Genome-wide prediction of cis-regulatory regions using supervised deep learning methods. BMC Bioinformatics 19, 202 (2018).
Johnson, D. S., Mortazavi, A., Myers, R. M. & Wold, B. Genome-wide mapping of in vivo protein-DNA interactions. Science 316, 1497–1502 (2007).
Barski, A. et al. High-resolution profiling of histone methylations in the human genome. Cell 129, 823–837 (2007).
Robertson, G. et al. Genome-wide profiles of STAT1 DNA association using chromatin immunoprecipitation and massively parallel sequencing. Nat. Methods 4, 651–657 (2007).
Park, P. J. ChIP-seq: advantages and challenges of a maturing technology. Nat. Rev. Genet. 10, 669–680 (2009).
Weirauch, M. T. et al. Evaluation of methods for modeling transcription factor sequence specificity. Nat. Biotechnol. 31, 126 (2013).
Lee, D., Karchin, R. & Beer, M. A. Discriminative prediction of mammalian enhancers from DNA sequence. Genome Res. 21, 2167–2180 (2011).
Ghandi, M., Lee, D., Mohammad-Noori, M. & Beer, M. A. Enhanced regulatory sequence prediction using gapped k-mer features. PLOS Comput. Biol. 10, e1003711 (2014).
Stormo, G. D., Schneider, T. D., Gold, L. & Ehrenfeucht, A. Use of the ‘Perceptron’ algorithm to distinguish translational initiation sites in E. coli. Nucleic Acids Res. 10, 2997–3011 (1982).
Stormo, G. D. DNA binding sites: representation and discovery. Bioinformatics 16, 16–23 (2000).
D’haeseleer, P. What are DNA sequence motifs? Nat. Biotechnol. 24, 423–425 (2006).
Kelley, D. R., Snoek, J. & Rinn, J. L. Basset: learning the regulatory code of the accessible genome with deep convolutional neural networks. Genome Res. 26, 990–999 (2016). This paper describes the application of a deep CNN to predict chromatin accessibility in 164 cell types from DNA sequence.
Wang, M., Tai, C., E, W. & Wei, L. DeFine: deep convolutional neural networks accurately quantify intensities of transcription factor-DNA binding and facilitate evaluation of functional non-coding variants. Nucleic Acids Res. 46, e69 (2018).
Kelley, D. R. et al. Sequential regulatory activity prediction across chromosomes with convolutional neural networks. Genome Res. 28, 739–750 (2018). In this paper, a deep CNN was trained to predict more than 4,000 genomic measurements including gene expression as measured by cap analysis of gene expression (CAGE) for every 150 bp in the genome using a receptive field of 32 kb.
Schreiber, J., Libbrecht, M., Bilmes, J. & Noble, W. Nucleotide sequence and DNaseI sensitivity are predictive of 3D chromatin architecture. Preprint at bioRxiv https://doi.org/10.1101/103614 (2018).
Zeng, H. & Gifford, D. K. Predicting the impact of non-coding variants on DNA methylation. Nucleic Acids Res. 45, e99 (2017).
Angermueller, C., Lee, H. J., Reik, W. & Stegle, O. DeepCpG: accurate prediction of single-cell DNA methylation states using deep learning. Genome Biol. 18, 67 (2017).
Zhou, J. et al. Deep learning sequence-based ab initio prediction of variant effects on expression and disease risk. Nat. Genet. 50, 1171–1179 (2018). In this paper, two models, a deep CNN and a linear model, are stacked to predict tissue-specific gene expression from DNA sequence, which demonstrates the utility of this approach in non-coding variant effect prediction.
Cuperus, J. T. et al. Deep learning of the regulatory grammar of yeast 5’ untranslated regions from 500,000 random sequences. Genome Res. 27, 2015–2024 (2017).
Pan, X. & Shen, H.-B. RNA-protein binding motifs mining with a new hybrid deep learning based cross-domain knowledge integration approach. BMC Bioinformatics 18, 136 (2017).
Avsec, Ž., Barekatain, M., Cheng, J. & Gagneur, J. Modeling positional effects of regulatory sequences with spline transformations increases prediction accuracy of deep neural networks. Bioinformatics 34, 1261–1269 (2018).
Budach, S. & Marsico, A. pysster: classification of biological sequences by learning sequence and structure motifs with convolutional neural networks. Bioinformatics 34, 3035–3037 (2018).
Cheng, S. et al. MiRTDL: a deep learning approach for miRNA target prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 13, 1161–1169 (2016).
Kim, H. K. et al. Deep learning improves prediction of CRISPR-Cpf1 guide RNA activity. Nat. Biotechnol. 36, 239–241 (2018).
Koh, P. W., Pierson, E. & Kundaje, A. Denoising genome-wide histone ChIP-seq with convolutional neuralnetworks. Bioinformatics 33, i225–i233 (2017).
Zhang, Y. et al. Enhancing Hi-C data resolution with deep convolutional neural network HiCPlus. Nat. Commun. 9, 750 (2018).
Nielsen, A. A. K. & Voigt, C. A. Deep learning to predict the lab-of-origin of engineered DNA. Nat. Commun. 9, 3135 (2018).
Luo, R., Sedlazeck, F. J., Lam, T.-W. & Schatz, M. Clairvoyante: a multi-task convolutional deep neural network for variant calling in single molecule sequencing. Preprint at bioRxiv https://doi.org/10.1101/310458 (2018).
Poplin, R. et al. A universal SNP and small-indel variant caller using deep neural networks. Nat. Biotechnol. 36, 983–987 (2018). In this paper, a deep CNN is trained to call genetic variants from different DNA-sequencing technologies.
Jaganathan, K. et al. Predicting splicing from primary sequence with deep learning. Cell 176, 535–548 (2019).
Elman, J. L. Finding structure in time. Cogn. Sci. 14, 179–211 (1990).
Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735–1780 (1997).
Bai, S., Zico Kolter, J. & Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. Preprint at arXiv https://arxiv.org/abs/1803.01271 (2018).
Pan, X., Rijnbeek, P., Yan, J. & Shen, H.-B. Prediction of RNA-protein sequence and structure binding preferences using deep convolutional and recurrent neural networks. BMC Genomics 19, 511 (2018).
Quang, D. & Xie, X. DanQ: a hybrid convolutional and recurrent deep neural network for quantifying the function of DNA sequences. Nucleic Acids Res. 44, e107 (2016).
Quang, D. & Xie, X. FactorNet: a deep learning framework for predicting cell type specific transcription factor binding from nucleotide-resolution sequential data. Preprint at bioRxiv https://doi.org/10.1101/151274 (2017).
Lee, B., Baek, J., Park, S. & Yoon, S. in Proceedings of the 7th ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics 434–442 (ACM, 2016).
Park, S., Min, S., Choi, H. & Yoon, S. deepMiRGene: deep neural network based precursor microRNA prediction. Preprint at arXiv https://arxiv.org/abs/1605.00017 (2016).
Boža, V., Brejová, B. & Vinař;, T. DeepNano: deep recurrent neural networks for base calling in MinION nanopore reads. PLOS ONE 12, e0178751 (2017).
Mikheyev, A. S. & Tin, M. M. Y. A first look at the Oxford Nanopore MinION sequencer. Mol. Ecol. Resour. 14, 1097–1102 (2014).
Barabási, A.-L., Gulbahce, N. & Loscalzo, J. Network medicine: a network-based approach to human disease. Nat. Rev. Genet. 12, 56–68 (2011).
Mitra, K., Carvunis, A.-R., Ramesh, S. K. & Ideker, T. Integrative approaches for finding modular structure in biological networks. Nat. Rev. Genet. 14, 719–732 (2013).
Scarselli, F., Gori, M., Tsoi, A. C., Hagenbuchner, M. & Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 20, 61–80 (2009).
Defferrard, M., Bresson, X. & Vandergheynst, P. in Advances in Neural Information Processing Systems 29 (NIPS 2016) (eds Lee, D. D., Sugiyama, M., Luxburg, U. V., Guyon, I. & Garnett, R.) 3844–3852 (Curran Associates Inc., 2016).
Kipf, T. N. & Welling, M. Semi-supervised classification with graph convolutional networks. Preprint at arXiv https://arxiv.org/abs/1609.02907 (2016).
Battaglia, P. W. et al. Relational inductive biases, deep learning, and graph networks. Preprint at arXiv https://arxiv.org/abs/1806.01261 (2018).
Hamilton, W. L., Ying, R. & Leskovec, J. Inductive representation learning on large graphs. Preprint at arXiv https://arxiv.org/abs/1706.02216 (2017).
Chen, J., Ma, T. & Xiao, C. FastGCN: fast learning with graph convolutional networks via importance sampling. Preprint at arXiv https://arxiv.org/abs/1801.10247 (2018).
Zitnik, M. & Leskovec, J. Predicting multicellular function through multi-layer tissue networks. Bioinformatics 33, i190–i198 (2017).
Zitnik, M., Agrawal, M. & Leskovec, J. Modeling polypharmacy side effects with graph convolutional networks. Bioinformatics 34, i457–i466 (2018).
Duvenaud, D. K. et al. in Advances in Neural Information Processing Systems 28 (NIPS 2015) (eds Cortes, C., Lawrence, N. D., Lee, D. D., Sugiyama, M. & Garnett, R.) 2224–2232 (Curran Associates Inc., 2015).
Kearnes, S., McCloskey, K., Berndl, M., Pande, V. & Riley, P. Molecular graph convolutions: moving beyond fingerprints. J. Comput. Aided Mol. Des. 30, 595–608 (2016).
Dutil, F., Cohen, J. P., Weiss, M., Derevyanko, G. & Bengio, Y. Towards gene expression convolutions using gene interaction graphs. Preprint at arXiv https://arxiv.org/abs/1806.06975 (2018).
Rhee, S., Seo, S. & Kim, S. in Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence 3527–3534 (IJCAI, 2018).
Chen, Z., Badrinarayanan, V., Lee, C.-Y. & Rabinovich, A. GradNorm: gradient normalization for adaptive loss balancing in deep multitask networks. Preprint at arXiv https://arxiv.org/abs/1711.02257 (2017).
Sung, K. & Poggio, T. Example-based learning for view-based human face detection. IEEE Trans. Pattern Anal. Mach. Intell. 20, 39–51 (1998).
Felzenszwalb, P. F., Girshick, R. B., McAllester, D. & Ramanan, D. Object detection with discriminatively trained part-based models. IEEE Trans. Pattern Anal. Mach. Intell. 32, 1627–1645 (2010).
Guo, M., Haque, A., Huang, D.-A., Yeung, S. & Fei-Fei, L. in Computer Vision – ECCV 2018 (eds Ferrari, V., Hebert, M., Sminchisescu, C. & Weiss, Y.) Vol. 11220 282–299 (Springer International Publishing, 2018).
Sundaram, L. et al. Predicting the clinical impact of human mutation with deep neural networks. Nat. Genet. 50, 1161–1170 (2018).
Zitnik, M. et al. Machine learning for integrating data in biology and medicine: principles, practice, and opportunities. Inf. Fusion 50, 71–91 (2018).
Yosinski, J., Clune, J., Bengio, Y. & Lipson, H. in Advances in Neural Information Processing Systems 27 (NIPS 2014) (eds Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N. D. & Weinberger, K. Q.) 3320–3328 (Curran Associates Inc., 2014).
Kornblith, S., Shlens, J. & Le, Q. V. Do better ImageNet models transfer better? Preprint at arXiv https://arxiv.org/abs/1805.08974 (2018).
Russakovsky, O. et al. ImageNet large scale visual recognition challenge. Preprint at arXiv https://arxiv.org/abs/1409.0575 (2014).
Esteva, A. et al. Dermatologist-level classification of skin cancer with deep neural networks. Nature 542, 115–118 (2017).
Pawlowski, N., Caicedo, J. C., Singh, S., Carpenter, A. E. & Storkey, A. Automating morphological profiling with generic deep convolutional networks. Preprint at bioRxiv https://doi.org/10.1101/085118 (2016).
Zeng, T., Li, R., Mukkamala, R., Ye, J. & Ji, S. Deep convolutional neural networks for annotating gene expression patterns in the mouse brain. BMC Bioinformatics 16, 147 (2015).
Zhang, W. et al. in IEEE Transactions on Big Data (IEEE, 2018).
Adam, P. et al. Automatic differentiation in PyTorch. Presented at 31st Conference on Neural Information Processing Systems (NIPS 2017).
Abadi, M. et al. Tensorflow: large-scale machine learning on heterogeneous distributed systems. Preprint at arXiv https://arxiv.org/abs/1603.04467 (2016).
Avsec, Z. et al. Kipoi: accelerating the community exchange and reuse of predictive models for genomics. Preprint at bioRxiv https://doi.org/10.1101/375345 (2018).This paper describes a platform to exchange trained predictive models in genomics including deep neural networks.
Breiman, L. Statistical modeling: the two cultures (with comments and a rejoinder by the author). Stat. Sci. 16, 199–231 (2001).
Greenside, P., Shimko, T., Fordyce, P. & Kundaje, A. Discovering epistatic feature interactions from neural network models of regulatory DNA sequences. Bioinformatics 34, i629–i637 (2018).
Zeiler, M. D. & Fergus, R. in Computer Vision – ECCV 2014 (eds Fleet, D., Pajdla, T., Schiele, B. & Tuytelaars, T.) Vol. 8689 818–833 (Springer International Publishing, 2014).
Simonyan, K., Vedaldi, A. & Zisserman, A. Deep inside convolutional networks: visualising image classification models and saliency maps. Preprint at arXiv https://arxiv.org/abs/1312.6034 (2013).
Shrikumar, A., Greenside, P., Shcherbina, A. & Kundaje, A. Not just a black box: learning important features through propagating activation differences. Preprint at arXiv https://arxiv.org/abs/1605.01713 (2016). This paper introduces DeepLIFT, a neural network interpretation method that highlights inputs most influential for the prediction.
Sundararajan, M., Taly, A. & Yan, Q. Axiomatic attribution for deep networks. Preprint at arXiv https://arxiv.org/abs/1703.01365 (2017).
Lanchantin, J., Singh, R., Wang, B. & Qi, Y. Deep motif dashboard: visualizing and understanding genomic sequences using deep neural networks. Pac. Symp. Biocomput. 22, 254–265 (2017).
Shrikumar, A. et al. TF-MoDISco v0.4.4.2-alpha: technical note. Preprint at arXiv https://arxiv.org/abs/1811.00416v2 (2018).
Ma, J. et al. Using deep learning to model the hierarchical structure and function of a cell. Nat. Methods 15, 290–298 (2018).
Hinton, G. E. & Salakhutdinov, R. R. Reducing the dimensionality of data with neural networks. Science 313, 504–507 (2006).
Kramer, M. A. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 37, 233–243 (1991).
Vincent, P., Larochelle, H., Bengio, Y. & Manzagol, P.-A. in Proceedings of the 25th International Conference on Machine Learning 1096–1103 (ACM, 2008).
Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y. & Manzagol, P.-A. Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 11, 3371–3408 (2010).
Jolliffe, I. in International Encyclopedia of Statistical Science (ed. Lovric, M.) 1094–1096 (Springer Berlin Heidelberg, 2011).
Plaut, E. From principal subspaces to principal components with linear autoencoders. Preprint at arXiv https://arxiv.org/abs/1804.10253 (2018).
Kunin, D., Bloom, J. M., Goeva, A. & Seed, C. Loss landscapes of regularized linear autoencoders. Preprint at arXiv https://arxiv.org/abs/1901.08168 (2019).
Scholz, M., Kaplan, F., Guy, C. L., Kopka, J. & Selbig, J. Non-linear PCA: a missing data approach. Bioinformatics 21, 3887–3895 (2005).
Tan, J., Hammond, J. H., Hogan, D. A. & Greene, C. S. ADAGE-based integration of publicly available Pseudomonas aeruginosa gene expression data with denoising autoencoders illuminates microbe-host interactions. mSystems 1, e00025–15 (2016).
Tan, J. et al. ADAGE signature analysis: differential expression analysis with data-defined gene sets. BMC Bioinformatics 18, 512 (2017).
Tan, J. et al. Unsupervised extraction of stable expression signatures from public compendia with an ensemble of neural networks. Cell Syst. 5, 63–71 (2017).
Brechtmann, F. et al. OUTRIDER: a statistical method for detecting aberrantly expressed genes in RNA sequencing data. Am. J. Hum. Genet. 103, 907–917 (2018).
Ding, J., Condon, A. & Shah, S. P. Interpretable dimensionality reduction of single cell transcriptome data with deep generative models. Nat. Commun. 9, 2002 (2018).
Cho, H., Berger, B. & Peng, J. Generalizable and scalable visualization of single-cell data using neural networks. Cell Syst. 7, 185–191 (2018).
Deng, Y., Bao, F., Dai, Q., Wu, L. & Altschuler, S. Massive single-cell RNA-seq analysis and imputation via deep learning. Preprint at bioRxiv https://doi.org/10.1101/315556 (2018).
Talwar, D., Mongia, A., Sengupta, D. & Majumdar, A. AutoImpute: autoencoder based imputation of single-cell RNA-seq data. Sci. Rep. 8, 16329 (2018).
Amodio, M. et al. Exploring single-cell data with deep multitasking neural networks. Preprint at bioRxiv https://doi.org/10.1101/237065 (2019).
Eraslan, G., Simon, L. M., Mircea, M., Mueller, N. S. & Theis, F. J. Single-cell RNA-seq denoising using a deep count autoencoder. Nat. Commun. 10, 390 (2019).
Lin, C., Jain, S., Kim, H. & Bar-Joseph, Z. Using neural networks for reducing the dimensions of single-cell RNA-Seq data. Nucleic Acids Res. 45, e156 (2017).
Kingma, D. P. & Welling, M. Auto-encoding variational bayes. Preprint at arXiv https://arxiv.org/abs/1312.6114 (2013).
Goodfellow, I. et al. in Advances in Neural Information Processing Systems 27 (NIPS 2014) (eds Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N. D. & Weinberger, K. Q.) 2672–2680 (Curran Associates Inc., 2014).
Lopez, R., Regier, J., Cole, M. B., Jordan, M. I. & Yosef, N. Deep generative modeling for single-cell transcriptomics. Nat. Methods 15, 1053–1058 (2018).
Way, G. P. & Greene, C. S. in Biocomputing 2018: Proceedings of the Pacific Symposium (eds Altman, R. B. et al.) 80–91 (World Scientific, 2018).
Grønbech, C. H. et al. scVAE: variational auto-encoders for single-cell gene expression data. Preprint at bioRxiv https://doi.org/10.1101/318295 (2018).
Wang, D. & Gu, J. VASC: dimension reduction and visualization of single-cell RNA-seq data by deep variational autoencoder. Genomics Proteomics Bioinformatics 16, 320–331 (2018).
Lotfollahi, M., Alexander Wolf, F. & Theis, F. J. Generative modeling and latent space arithmetics predict single-cell perturbation response across cell types, studies and species. Preprint at bioRxiv https://doi.org/10.1101/478503 (2018).
Hu, Q. & Greene, C. S. Parameter tuning is a key part of dimensionality reduction via deep variational autoencoders for single cell RNA transcriptomics. Preprint at bioRxiv https://doi.org/10.1101/385534 (2018).
Gupta, A. & Zou, J. Feedback GAN (FBGAN) for DNA: a novel feedback-loop architecture for optimizing protein functions. Preprint at arXiv https://arxiv.org/abs/1804.01694 (2018).
Killoran, N., Lee, L. J., Delong, A., Duvenaud, D. & Frey, B. J. Generating and designing DNA with deep generative models. Preprint at arXiv https://arxiv.org/abs/1712.06148 (2017).
Ghahramani, A., Watt, F. M. & Luscombe, N. M. Generative adversarial networks simulate gene expression and predict perturbations in single cells. Preprint at bioRxiv https://doi.org/10.1101/262501 (2018).
Amodio, M. & Krishnaswamy, S. MAGAN: aligning biological manifolds. Preprint at arXiv https://arxiv.org/abs/1803.00385 (2018).
Maurano, M. T. et al. Systematic localization of common disease-associated variation in regulatory DNA. Science 337, 1190–1195 (2012).
Cheng, J. et al. MMSplice: modular modeling improves the predictions of genetic variant effects on splicing. Genome Biol. 20, 48 (2019).
van der Maaten, L. in Proceedings of the Twelfth International Conference on Artificial Intelligence and Statistics (eds van Dyk, D. & Welling, M.) Vol. 5 384–391 (PMLR, 2009).
Angerer, P. et al. Single cells make big data: new challenges and opportunities in transcriptomics. Curr. Opin. Syst. Biol. 4, 85–91 (2017).
Shaham, U. et al. Removal of batch effects using distribution-matching residual networks. Bioinformatics 33, 2539–2546 (2017).
Regev, A. et al. The human cell atlas. eLife 6, e27041 (2017).
Fleming, N. How artificial intelligence is changing drug discovery. Nature 557, S55–S57 (2018).
Kalinin, A. A. et al. Deep learning in pharmacogenomics: from gene regulation to patient stratification. Pharmacogenomics 19, 629–650 (2018).
AlQuraishi, M. End-to-end differentiable learning of protein structure. Preprint at bioRxiv https://doi.org/10.1101/265231 (2018).
Nawy, T. Spatial transcriptomics. Nat. Methods 15, 30 (2018).
Eulenberg, P. et al. Reconstructing cell cycle and disease progression using deep learning. Nat. Commun. 8, 463 (2017).
KoneČný, J., McMahan, H. B., Ramage, D. & Richtárik, P. Federated optimization: distributed machine learning for on-device intelligence. Preprint at arXiv https://arxiv.org/abs/1610.02527 (2016).
Beaulieu-Jones, B. K. et al. Privacy-preserving generative deep neural networks support clinical data sharing. Preprint at bioRxiv https://doi.org/10.1101/159756 (2018).
Lever, J., Krzywinski, M. & Altman, N. Classification evaluation. Nat. Methods 13, 603 (2016).
Tieleman, T. & Hinton, G. Lecture 6.5 - RMSProp, COURSERA: neural networks for machine learning (2012).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Preprint at arXiv https://arxiv.org/abs/1412.6980 (2014).
Schmidhuber, J. Deep learning in neural networks: an overview. Neural Netw. 61, 85–117 (2015).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Bottou, L. in Proceedings of Neuro-Nımes ‘91 12 (EC2, 1991).
Bengio, Y. Practical recommendations for gradient-based training of deep architectures. Preprint at arXiv https://arxiv.org/abs/1206.5533 (2012).
Bergstra, J. & Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 13, 281–305 (2012).
Bergstra, J., Yamins, D. & Cox, D. in Proceedings of the 30th International Conference on Machine Learning Vol. 28 115–123 (JMLR W&CP, 2013).
Shahriari, B., Swersky, K., Wang, Z., Adams, R. P. & de Freitas, N. Taking the human out of the loop: a review of bayesian optimization. Proc. IEEE 104, 148–175 (2016).
Li, L., Jamieson, K., DeSalvo, G., Rostamizadeh, A. & Talwalkar, A. Hyperband: a novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 18, 6765–6816 (2017).
Elsken, T., Metzen, J. H. & Hutter, F. Neural architecture search: a survey. Preprint at arXiv https://arxiv.org/abs/1808.05377 (2018).
Acknowledgements
Ž.A. was supported by the German Bundesministerium für Bildung und Forschung (BMBF) through the project MechML (01IS18053F). The authors acknowledge M. Heinig and A. Raue for valuable feedback.
Reviewer information
Nature Reviews Genetics thanks C. Greene and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
The authors contributed equally to all aspects of the article.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Related links
DragoNN: https://kundajelab.github.io/dragonn/tutorials.html
Kaggle machine learning competitions: https://www.kaggle.com/sudalairajkumar/winning-solutions-of-kaggle-competitions
Keras: https://keras.io/
Keras model zoos: https://keras.io/applications/
PyTorch: http://pytorch.org
PyTorch model zoos: https://pytorch.org/docs/stable/torchvision/models.html
Tensorflow model zoos: https://github.com/tensorflow/models; https://www.tensorflow.org/hub/
Glossary
- Feature
-
An individual, measurable property or characteristic of a phenomenon being observed.
- Handcrafted features
-
Features derived from raw data (or other features) using manually specified rules. Unlike learned features, they are specified upfront and do not change during model training. For example, the GC content is a handcrafted feature of a DNA sequence.
- End-to-end models
-
Machine learning models that embed the entire data-processing pipeline to transform raw input data into predictions without requiring a preprocessing step.
- Deep neural networks
-
A wide class of machine learning models with a design that is loosely based on biological neural networks.
- Fully connected
-
Referring to a layer that performs an affine transformation of a vector followed by application of an activation function to each value.
- Convolutional
-
Referring to a neural network layer that processes data stored in n-dimensional arrays, such as images. The same fully connected layer is applied to multiple local patches of the input array. When applied to DNA sequences, a convolutional layer can be interpreted as a set of position weight matrices scanned across the sequence.
- Recurrent
-
Referring to a neural network layer that processes sequential data. The same neural network is applied at each step of the sequence and updates a memory variable that is provided for the next step.
- Graph convolutional
-
Referring to neural networks that process graph-structured data; they generalize convolution beyond regular structures, such as DNA sequences and images, to graphs with arbitrary structures. The same neural network is applied to each node and edge in the graph.
- Autoencoders
-
Unsupervised neural networks trained to reconstruct the input. One or more bottleneck layers have lower dimensionality than the input, which leads to compression of data and forces the autoencoder to extract useful features and omit unimportant features in the reconstruction.
- Generative adversarial networks
-
(GANs). Unsupervised learning models that aim to generate data points that are indistinguishable from the observed ones.
- Target
-
The desired output used to train a supervised model.
- Loss function
-
A function that is optimized during training to fit machine learning model parameters. In the simplest case, it measures the discrepancy between predictions and observations. In the case of quantitative predictions such as regression, mean-squared error loss is frequently used, and for binary classification, the binary cross-entropy, also called logistic loss, is typically used.
- k-mer
-
Character sequence of a certain length. For instance, a dinucleotide is a k-mer for which k = 2.
- Logistic regression
-
A supervised learning algorithm that predicts the log-odds of a binary output to be of the positive class as a weighted sum of the input features. Transformation of the log-odds with the sigmoid activation function leads to predicted probabilities.
- Sigmoid function
-
A function that maps real numbers to [0,1], defined as 1/(1 + e −x).
- Activation function
-
A function applied to an intermediate value x within a neural network. Activation functions are usually nonlinear yet very simple, such as the rectified-linear unit or the sigmoid function.
- Regularization
-
A strategy to prevent overfitting that is typically achieved by constraining the model parameters during training by modifying the loss function or the parameter optimization procedure. For example, the so-called L2 regularization adds the sum of the squares of the model parameters to the loss function to penalize large model parameters.
- Hidden layers
-
Layers are a list of artificial neurons that collectively represents a function that take as input an array of real numbers and returns an array of real numbers corresponding to neuron activations. Hidden layers are between the input and output layers.
- Rectified-linear unit
-
(ReLU). Widely used activation function defined as max(0, x).
- Neuron
-
The elementary unit of a neural network. An artificial neuron aggregates the inputs from other neurons and emits an output called activation. Inputs and activations of artificial neurons are real numbers. The activation of an artificial neuron is computed by applying a nonlinear activation function to a weighted sum of its inputs.
- Linear regression
-
A supervised learning algorithm that predicts the output as a weighted sum of the input features.
- Decision trees
-
Supervised learning algorithms in which the prediction is made by making a series of decisions of type ‘is feature i larger than x’ (internal nodes of the tree) and then predicting a constant value for all points satisfying the same decisions series (leaf nodes).
- Random forests
-
Supervised learning algorithms that train and average the predictions of many decision trees.
- Gradient-boosted decision trees
-
Supervised learning algorithms that train multiple decision trees in a sequential manner; at each time step, a new decision tree is trained on the residual or pseudo-residual of the previous decision tree.
- Position weight matrix
-
(PWM). A commonly used representation of sequence motifs in biological sequences. It is based on nucleotide frequencies of aligned sequences at each position and can be used for identifying transcription factor binding sites from DNA sequence.
- Overfitting
-
The scenario in which the model fits the training set very well but does not generalize well to unseen data. Very flexible models with many free parameters are prone to overfitting, whereas models with many fewer parameters than the training data do not overfit.
- Filters
-
Parameters of a convolutional layer. In the first layer of a sequence-based convolutional network, they can be interpreted as position weight matrices.
- Pooling operation
-
A function that replaces the output at a certain location with a summary statistic of the nearby outputs. For example, the max pooling operation reports the maximum output within a rectangular neighbourhood.
- Channel
-
An axis other than one of the positional axes. For images, the channel axis encodes different colours (such as red, green and blue), for one-hot-encoded sequences (A: [1, 0, 0, 0], C: [0, 1, 0, 0] and so on), it denotes the bases (A, C, G and T), and for the output of the convolutions, it corresponds to the outputs of different filters.
- Dilated convolutions
-
Filters that skip some values in the input layers. Typically, each subsequent convolutional layer increases the dilation by a factor of two, thus achieving an exponentially increasing receptive field with each additional layer.
- Receptive field
-
The region of the input that affects the output of a convolutional neuron.
- Memory
-
An array that stores the information of the patterns observed in the sequence elements previously processed by a recurrent neural network.
- Feature importance scores
-
The quantification values of the contributions of features to a current model prediction. The simplest way to obtain this score is to perturb the feature value and measure the change in the model prediction: the larger the change found, the more important the feature is.
- Backpropagation
-
An algorithm for computing gradients of neural networks. Gradients with respect to the loss function are used to update the neural network parameters during training.
- Saliency maps
-
Feature importance scores defined as the gradient absolute values of the model output with respect to the model input.
- Input-masked gradients
-
Feature importance scores defined as the gradient of the model output with respect to the model input multiplied by the input values.
- Automatic differentiation
-
A set of techniques, which consist of a sequence of elementary arithmetic operations, used to automatically differentiate a computer program.
- Model architecture
-
The structure of a neural network independent of its parameter values. Important aspects of model architecture are the types of layers, their dimensions and how they are connected to each other.
- k-means
-
An unsupervised method for partitioning the observations into clusters by alternating between refining cluster centroids and updating cluster assignments of observations.
- Principal component analysis
-
An unsupervised learning algorithm that linearly projects data from a high-dimensional space to a lower-dimensional space while retaining as much variance as possible.
- t-Distributed stochastic neighbour embedding
-
(t-SNE). An unsupervised learning algorithm that projects data from a high-dimensional space to a lower-dimensional space (typically 2D or 3D) in a nonlinear fashion while trying to preserve the distances between points.
- Latent variable models
-
Unsupervised models describing the observed distribution by imposing latent (unobserved) variables for each data point. The simplest example is the mixture of Gaussian values.
- Bottleneck layer
-
A neural network layer that contains fewer neurons than previous and subsequent layers.
- Generative models
-
Models able to generate points from the desired distribution. Deep generative models are often implemented by a neural network that transforms samples from a standard distribution (normal and uniform) into samples from a complex distribution (gene expression levels or sequences that encode a splice site).
- Hyperparameters
-
Parameters specifying the model or the training procedure that are not optimized by the learning algorithm (for example, by the stochastic gradient descent algorithm). Examples of hyperparameters are the number of layers, regularization strength, batch size and the optimization step size.
Rights and permissions
About this article
Cite this article
Eraslan, G., Avsec, Ž., Gagneur, J. et al. Deep learning: new computational modelling techniques for genomics. Nat Rev Genet 20, 389–403 (2019). https://doi.org/10.1038/s41576-019-0122-6
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41576-019-0122-6
This article is cited by
-
DiCleave: a deep learning model for predicting human Dicer cleavage sites
BMC Bioinformatics (2024)
-
Pathogenomics for accurate diagnosis, treatment, prognosis of oncology: a cutting edge overview
Journal of Translational Medicine (2024)
-
Genomic prediction using machine learning: a comparison of the performance of regularized regression, ensemble, instance-based and deep learning methods on synthetic and empirical data
BMC Genomics (2024)
-
Hold out the genome: a roadmap to solving the cis-regulatory code
Nature (2024)
-
Microfluidic high-throughput 3D cell culture
Nature Reviews Bioengineering (2024)