Abstract
Bose–Einstein condensation (BEC) is a quantum phenomenon in which a macroscopic number of bosons occupy the lowest energy state and acquire coherence at low temperatures. In three-dimensional antiferromagnets, a magnetic-field-induced transition has been successfully described as a magnon BEC. For a strictly two-dimensional (2D) system, it is known that BEC cannot take place due to the presence of a finite density of states at zero energy. However, in a realistic quasi-2D magnet consisting of stacked magnetic layers, a small but finite interlayer coupling stabilizes marginal BEC but such that 2D physics is still expected to dominate. This 2D-limit BEC behaviour has been reported in a few materials but only at very high magnetic fields that are difficult to access. The honeycomb S = 1/2 Heisenberg antiferromagnet YbCl3 exhibits a transition to a fully polarized state at a relatively low in-plane magnetic field. Here, we demonstrate the formation of a quantum critical 2D Bose gas at the transition field, which, with lowering the field, experiences a BEC marginally stabilized by an extremely small interlayer coupling. Our observations establish YbCl3, previously a Kitaev quantum spin liquid material, as a realization of a quantum critical BEC in the 2D limit.
Similar content being viewed by others
Main
XY antiferromagnetism induced by an applied magnetic field H provides a prominent example of Bose–Einstein condensation (BEC)1,2 in quantum magnets3,4,5, which has been established in a wide variety of magnets including spin-singlet dimers TlCuCl3 (refs. 6,7), BaCuSi2O6 (refs. 8,9) and S = 1 magnet with a single ion anisotropy NiCl2-4SC(NH2)2 (ref. 10). Consider, for example, the case for a Heisenberg antiferromagnet with a nearest-neighbour coupling J in a field H. H along the z-direction polarizes the spins and causes their z-component <Sz> to acquire a finite value. When H is close to the saturation field Hs—that is, near a quantum phase transition to a fully polarized (FP) state—the system effectively becomes an XY antiferromagnet with the remaining x- and y-components of the spins, Sx and Sy. As Sx and Sy can be replaced with creation/annihilation operators of bosons, the system can be mapped onto an ensemble of interacting bosons with boson operators bk+ and bk in the momentum k representation, an excitation energy εk and an effective chemical potential μeff (ref. 11), which is described by the following Hamiltonian:
In this mapping, εk is determined by the energy dispersion of a tight-binding band with a nearest-neighbour hopping t = J/2 measured from the bottom of the band. The effective chemical potential
consists of the bare chemical potential controlled by Hs − H and an additional term representing the increase of the mean-field, one-particle energy due to a repulsive boson–boson interaction Ueff, which arises from the JSziSzj term in the original spin Hamiltonian and is on the order of J in the bare form6,12. <n> is the average number of (hole) bosons per site, which corresponds to the deviation of field-induced magnetization <Sz> from the saturation value. The XY ordering below Hs can therefore be treated as a BEC of a low density of interacting bosons in the Hamiltonian. The FP state above Hs has an excitation gap and zero boson density <n> = 0 at temperature T = 0 and can be regarded as the vacuum state of the bosons. The field-induced quantum phase transition at Hs provides us with a unique opportunity to study a BEC quantum critical point (BEC-QCP).
The nature of the magnetic-field-induced BEC depends sensitively on the dimensionality of the system. In a three-dimensional (3D) magnet, BEC occurs simply as a long-range XY ordering. Distinct from the 3D case is a two-dimensional (2D) magnet. It is known that a strictly 2D Bose gas does not experience BEC at a finite temperature, due to the presence of a finite density of states at zero energy and the associated logarithmic divergence of the number integral in the T = 0 limit. In the original language of spin, a long-range XY ordering in a strictly 2D magnet is suppressed by strong fluctuations down to T = 0 (ref. 13). Instead, a quasi-long-range-order (quasi-LRO) emerges: that is, the Berezinskii–Kosterlitz–Thouless (BKT) transition14,15,16. One therefore observes a BKT near Hs in strictly 2D systems, instead of the BEC. The effective boson–boson interaction Ueff in 2D is distinct from those in 3D and is subject to logarithmic renormalization as Ueff = U0/(−ln<n>), where U0 is the bare interaction and suppressed appreciably around the QCP17. In reality, the bulk ‘2D magnet’ that we investigate experimentally is not a strictly 2D magnet but a quasi-2D magnet, which comprises a stack of strictly 2D magnets with a small but finite interlayer coupling (J⊥). The interlayer coupling should marginally push the system from a BKT transition to a 3D LRO and hence a BEC. Even in such a quasi-2D BEC state, however, 2D physics could be still relevant at temperatures above the temperature scale of J⊥. 2D logarithmic renormalization of Ueff, for example, may still be captured. Possible signatures of BKT physics were suggested theoretically18 and experimentally19,20,21,22 in quasi-2D magnets with intrinsic XY character.
It is tempting to explore such a distinct class of marginal BEC in the 2D limit and its BEC-QCP in quasi-2D antiferromagnets under magnetic fields, where we anticipate 2D logarithmic renormalization, 2D quantum and thermal fluctuations with possible signatures of BKT physics and an interplay with 3D physics arising from a minute interlayer coupling J⊥. So far, despite the long history of BEC and BEC-QCP in antiferromagnets, such exploration for the 2D limit has been limited due to the lack of an appropriate model system. The quasi-2D dimer system BaCu2Si2O6 shows a magnetic-field-induced BEC above the QCP where a finite magnetization emerges. The reduction of the effective interlayer coupling due to frustration was argued to play a vital role9. The linear decrease of the transition temperature Tc as a function of the magnetic field around QCP, which is expected for a BEC in the 2D limit23, suggests the presence of 2D quantum fluctuations. However, the frustration scenario was challenged by the later observation of ferromagnetic interlayer coupling. The presence of two types of dimers does not allow for a straightforward interpretation of the critical behaviour24. More importantly, signatures of ‘2D’ critical fluctuations other than the linear scaling of transition temperature and underlying boson–boson interactions have not yet been unveiled, in contrast to the 3D case (for example, TlCuCl3 (ref. 6) and NiCl2-4SC(NH2)2 (ref. 25)), partly due to the very high magnetic field needed to reach the QCP. To capture the BEC criticality in the 2D limit experimentally, a material system with an easily accessible QCP is highly desired, where one can probe 2D quantum and thermal fluctuations and underlying interactions through other thermodynamic parameters in addition to Tc.
The pseudospin 1/2 Heisenberg antiferromagnet YbCl3 may be an ideal system for the exploration of the quasi-2D BEC-QCP. The material has the 2D honeycomb-based structure shown in the inset of Fig. 1a (ref. 26) and was earlier suggested as a possible Kitaev magnet with anisotropic bond-dependent couplings27. Recent inelastic neutron-scattering measurements, however, revealed that the system is a quasi-2D Heisenberg antiferromagnet with an almost isotropic in-plane nearest-neighbour coupling J ≈ 5 K (= 0.42 meV) and a very small interlayer coupling |J⊥/J| ≈ 3 × 10−5 (ref. 28). Recent quantum Monte Carlo (QMC) simulations on this system indicate a ferromagnetic interlayer coupling at least smaller than |J⊥/J| ≈ 2 × 10−3 (ref. 29), consistent with the estimate from the inelastic neutron-scattering measurement28. J⊥ is therefore extremely small, likely of the order of 0.1 mK and at most 10 mK, rendering this system ideal to explore a BEC close to the 2D limit. Specific heat and neutron diffraction measurements indicate the occurrence of a 3D long-range Néel ordering at TN = 0.6 K (ref. 30) with an ordered moment of ∼1 µB (refs. 27,28,30), which is stabilized by the small J⊥. Alternating-current susceptibility measurements indicate a magnetic-field-induced transition to a FP state at Hs = 6 and 9.5 T with the field applied in and out of plane, respectively27, which we argue to be a quasi-2D BEC-QCP.
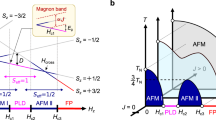
a, The magnetization M(H) curves at different temperatures. The Van Vleck contribution has been subtracted (Supplementary Fig. 1). The inset shows the honeycomb layered structure of YbCl3 (space group C12/m1)26,41 with an antiferromagnetic intralayer coupling J ≈ 5 K and a ferromagnetic interlayer coupling J⊥ ≈ 0.1 mK. b, The magnetic field dependence of entropy at different temperatures. c, The H–T phase diagram. The power α of the T-dependent specific heat C (C ∝ Tα defined as α(T) ≡ d ln C/d ln T) was evaluated by linear fits to ln C versus ln T for every four data points and is indicated by the colour. The open symbols indicate the Tc of the long-range magnetic ordering, defined by the position of peaks in dM/dT, C/T and dM/dH. The crosses represent the locations of the broad SRO peaks in C/T. Error bars for circles and crosses are defined by the peak width of the C(T)/T anomaly at 2% below the maximum value, which was determined by fitting 20–30 points around the peak with a polynomial curve. Filled squares indicate the gap size ∆ determined by C/T. A linear fit to ∆ is shown with dotted line above Hs. The grey broken line below Hs indicates the onset of the 2D thermal fluctuations above Tc, which is determined as the onset temperature of a rapid increase of C/T upon cooling (the open arrows in Fig. 2b). fluc., fluctuation.
We therefore have explored the quasi-2D BEC-QCP in YbCl3 with the in-plane magnetic field H as a tuning parameter of the quantum phase transition. At the QCP, we identified clear signatures of BEC quantum critical fluctuations in the 2D limit, which manifest themselves as the formation of a highly mobile, correlated 2D Bose gas in the dilute limit, where the effective boson–boson interaction is an order of magnitude smaller than those of its 3D analogues due to the expected logarithmic renormalization of boson–boson interaction. The finite temperature transitions below the saturation field Hs (that is, the QCP) can be described as a BEC induced by an extremely small interlayer coupling J⊥ of ~0.1 mK.
Heisenberg-like to XY-like crossover and the QCP
Single crystals of YbCl3 used in this study were grown by a chemical vapour-transport technique (Methods). The magnetic field was always applied along the in-plane a-direction, perpendicular to one of the honeycomb bonds. The magnetization M shown in Fig. 1a reaches the saturation moment Ms = 1.72 µB per Yb around Hs ≈ 5.9 T. The saturation field in the T = 0 limit, which marks the quantum phase transition, was estimated as Hs = 5.93 ± 0.01 T from the crossing point of dM/dH curves at 0.05 and 0.08 K (Supplementary Information and Supplementary Fig. 1).
At zero field, the specific heat divided by temperature C/T shown in Fig. 2b exhibits a broad peak from a short-range 2D antiferromagnetic correlation around 1.2 K, followed by a tiny but sharp peak from the long-range 3D Néel ordering at Tc = 0.65 K, fully consistent with the previous studies27,30. Weak signature of the Néel order is also present in M(T), which is more clearly visualized in the temperature derivative dM/dT (Fig. 2e,f). Upon applying H, Tc first increases until Hp ≈ 2–3 T and then decreases to zero at the saturation field Hs = 5.93 T (refs. 27,30). This evolution is summarized in the phase diagram shown in Fig. 1c. The initial increase of Tc indicates the suppression of fluctuations along the field direction and the crossover of symmetry from Heisenberg-like to XY-like, as discussed in a class of low-dimensional Heisenberg magnets31,32. The suppression of fluctuations can indeed be captured by the initial decrease of the isothermal entropy up to Hp at temperatures below 0.8 K in Fig. 1b, as well as a negative slope dM/dT|H(= dS/dH|T) in the same H- and T-range in Fig. 2a,e.
a,c, T-dependent M/H for H ≤ Hs (a) and H ≥ Hs (c). The arrows in a represent Tc determined from the singularity in dM/dT (e,f). b,d, T-dependent C/T for H ≤ Hs (b) and H ≥ Hs (d). Open triangles in b mark the onset temperature for thermal fluctuations towards Tc, where C/T starts to deviate from the constant behaviour upon cooling. e,f, T-dependence of the derivative of magnetization dM/dT below (e) and above (f) 3 T, respectively. The data at each field in e are shifted by 0.2 Am2 K−1 mol−1 for clarity.
Above Hp ≈ 2–3 T, the system should have predominant XY character. Reflecting this change of symmetry, the anomalies at Tc in C/T and M show qualitatively different behaviour from that of the zero-field limit. In C/T, the small λ-like peak associated with LRO and the broad peak associated with short-range ordering (SRO) merge at higher fields into one sharp cusp-like peak (Fig. 2b). The weak anomaly in dM/dT at low fields changes to a cusp-like anomaly near Hp (Fig. 2e,f). As H increases further towards Hs, the LRO with XY character is suppressed due to the reduced Sx and Sy degrees of freedom and Tc decreases to zero (Fig.1c). In this field region near Hs, the LRO with XY character is described as a quasi-2D BEC induced by interlayer coupling, as we will discuss below. In the language of bosons, the suppression of the quasi-2D BEC upon approaching the QCP at Hs can be described by a decrease of the boson density to zero.
Above Hs, we observe thermally activated behaviours of C and (Ms − M)/Ms at low temperatures (Supplementary Fig. 4a,b), indicating the emergence of a gap in the magnetic (boson) excitations in the FP state. The extracted activation energy ∆, as shown in Fig. 1c and Supplementary Fig. 4c, increases linearly from Hs as roughly gμB(Hs − H), where g ≈ 3.67 is the g-factor for S = 1/2 pseudospins (Supplementary Information). In the language of bosons, gμB(Hs − H) corresponds to the energy between the bare chemical potential μ and the bottom of the band and sets the excitation gap above Hs. These behaviours above Hp indicate that the honeycomb antiferromagnet YbCl3 under magnetic field is an excellent arena to explore a quasi-2D BEC and the associated BEC-QCP.
2D-limit BEC critical fluctuations at the QCP
At the saturation field Hs—that is, the QCP—we indeed find evidence for quantum fluctuations predicted for a BEC-QCP in the 2D limit. The critical behaviours of C(T), M(T) and Tc(H) at a field-induced BEC-QCP in d dimensions are predicted to be C ∝ Td/2, Ms − M ∝ Td/2 and Tc(H) ∝ (Hs − H)2/d (refs. 3,23,33,34). In the 3D BEC systems such as TlCuCl3 (ref. 6) and NiCl2-4SC(NH2)2 (ref. 25), the critical exponents with d = 3 were firmly established at the BEC-QCP. As summarized in Figs. 2b,c and 3a,b, in stark contrast to 3D model systems, all three parameters of YbCl3, C, M and Tc, closely follow the expected critical behaviour in the 2D (d = 2) limit at Hs. C is linear in T with a coefficient γ = C/T ≈ 1 J K−2 Yb-mol−1 over a wide T range below ~1.2 K. M decreases linearly with T from the saturation moment as M = Ms − Ms(T/T0) with T0 = 11 K. In the language of bosons, the boson density <n> ≡ (Ms − M)/Ms = T/T0 goes to zero at T = 0. Tc scales linearly with Hs − H near the critical point Hs. These quantum critical behaviours can be utilized as markers for quantum fluctuations. The power exponent of C(T), α(T) ≡ d ln C/d ln T, is indicated as a colour contour map on the H–T phase diagram in Fig. 1c. The red region for α ≈ 1, which represents BEC criticality in the 2D limit, spreads like a fan from the QCP at Hs. The contour map of dM/dT yields essentially the same quantum critical region (Supplementary Information). The fanlike spread is indeed the canonical behaviour of a quantum critical regime around the QCP, which confirms that the critical exponents, which are consistent with a BEC-QCP in the 2D limit, arise from quantum critical fluctuations. The 2D quantum critical behaviour is observed at least down to our lowest temperature of measurements, T = 50 mK. We note that 50 mK is only 1% of J = 5 K but still orders of magnitude higher than the energy scale of J⊥, which is on the order of 0.1 mK based on previous neutron-scattering studies and our analysis below. A substantial part of the 3D critical behaviour originating from the small J⊥ is very likely hidden in the low-temperature limit below experimentally accessible temperatures.
a, Temperature dependence of boson density <n> = 1 − M/Ms for various magnetic fields H around the QCP. The dashed line represents <n> = T/T0, and T0 = 11 K = 2.2J. The arrows indicate Tc determined from the peak in dM/dT (Fig. 2e,f). The solid line represents <nc> = DkBTBEC(−ln(kBTBEC/Ec) + 2) with a cut-off energy Ec = 0.2 mK and D = √3/2πJ for J = 5 K (Fig. 3c). b, Full logarithmic plot of Tc as a function of Hs − H, with Hs = 5.93 T. The dashed and the broken lines represent Tc ∝ (Hs − H) and (Hs − H)2/3 expected for 2D and 3D, respectively. c, The dilute Bose gas model used to analyse C(T) and M(T) around the QCP. The density of states D(E) for the 2D honeycomb tight-binding model has a bandwidth of 3J and a finite value at E = 0, D = √3/2πJ. In the presence of a small interlayer coupling J⊥(«J), a 3D density of states with D(E) proportional to √E shows up at the bottom of the band over the scale of J⊥. The effective chemical potential μeff(T) = gμB(Hs − H) − 2Ueff<n> approaches E = 0 linearly with T at H = Hs. For H < Hs, μeff goes to zero at a finite temperature due to the suppression of the logarithmic divergence by the 3D DOS below Ec. d, The effective boson–boson interaction Ueff versus the critical boson density <nc>. Ueff at <nc> → 0 (H = Hs, cross) was estimated from the linear T-dependence of <n>. For H < Hs, Ueff was estimated from <nc> at Tc(H) in a (triangles) and at Hc(T) in Supplementary Fig. 1c (squares) by using Ueff = gμB(Hs − H)/2<nc>. The broken line represents the <nc> dependence of Ueff with 2D logarithmic renormalization and a cut-off by J⊥, phenomenologically expressed by Ueff = −U0(1/ln<nc> + 1/ln(J⊥/J)). A bare boson–boson interaction U0 = 6 K = 1.2J and J⊥/J = 2 × 10−5 are used.
An interacting 2D Bose gas in the dilute limit at the QCP
The quasi-2D BEC-QCP lies at the limit of zero boson density, where the system hosts a dilute and therefore weakly interacting boson gas produced by thermal excitations at a finite temperature. Let us consider a 2D boson gas with a constant density of states D(E) = D and an effective chemical potential µeff = gμB(Hs − H) − 2Ueff<n>, as shown in Fig. 3c. For a tight-binding model on the 2D honeycomb lattice with nearest-neighbour hopping t = J/2, D = √3/2πJ at the bottom of the band (energy E = 0) (Supplementary Information). From the number integral with the Bose function, <n> and µeff are related by the following equation:
where kB is the Boltzmann constant. At the QCP with H = Hs, µeff = −2Ueff<n>. Equation (2) then requires <n> and hence µeff to be linear in T, in accord with the BEC critical behaviour of <n> in the 2D limit. The experimentally obtained T-linear boson density from M in Fig. 3a, <n> = T/T0 (T0 = 11 K = 2.2J), yields Ueff = 1.2 K = 0.24J from equation (2). It is known that the free 2D Bose gas (Ueff = 0) with zero chemical potential has a T-linear C(T) at low temperatures with a linear coefficient γ = (π2/3)kB2D, the same expression as that of a free Fermi gas. With D = √3/2πJ and J = 5 K, the free boson γ is 1.5 J K−2 mol−1. We find that the T-linear negative shift of the chemical potential from zero, µeff = −2Ueff<n> = −0.21kBT, reduces the γ value from the free boson value to 0.99 J K−2 mol−1, in excellent agreement with the experimental data (Supplementary Information). These results firmly justify the estimate of Ueff and µeff and, more importantly, the 2D Bose gas description. The BEC quantum criticality in the 2D limit manifests itself as the formation of an interacting 2D Bose gas at the zero-density limit.
Ueff = 0.24J is an order of magnitude smaller than those estimated for prototypical 3D BEC systems, 5J for TlCuCl3 (refs. 35,36) and 3J for NiCl2-4SC(NH2)2 (ref. 37). We argue that this represents the logarithmic renormalization of boson–boson scattering U0 unique to 2D, Ueff ≈ −U0/ln<n> (ref. 17) and mirrors the 2D character of quantum critical Bose gas in YbCl3. The 2D renormalization alone would bring Ueff to zero at the quantum critical point due to the logarithmic divergence. We argue that Ueff stays at a finite value ~0.24J even at the QCP here due to the weak three-dimensionality associated with the interlayer coupling J⊥, which suppresses the logarithmic singularity at the bottom of the band, as we discuss later. The cut-off of logarithmic divergence is roughly estimated as Uc ≈ −U0/ln (J⊥/J), which suggests −ln (J⊥/J) ≈ 10 for YbCl3.
BEC due to a finite interlayer coupling J ⊥
Lowering the applied magnetic field below Hs, which corresponds to boson doping, clear anomalies indicative of a phase transition emerge in the T-dependent C(T) and M(T) at Tc(H), as shown in Fig. 2. We found that Tc(H) can be quantitatively described as a BEC of 3D system by introducing an extremely small interlayer coupling J⊥ to a purely 2D band, which implies that the transitions are a long-range magnetic ordering stabilized by the interlayer coupling rather than the BKT transition for 2D. The presence of a small interlayer coupling J⊥ rounds the bottom of the purely 2D band and produces a corresponding √E-dependent density of states, as expected in 3D, within the extremely narrow energy range set by J⊥ (Fig. 3c). The continuously vanishing density of states at E = 0 prevents a logarithmic divergence of the number integral and hence gives rise to a BEC at a finite temperature. We approximate the rounding of the constant 2D density of states D(E) = D near the bottom of the band by introducing an energy cut-off Ec below which D(E) is replaced with the 3D density of states, √E/Ec. Ec is of the order of J⊥, roughly 2–3J⊥. By setting µeff = 0 in the number integral, a BEC occurs at <nc> and TBEC satisfying
The first and second terms in equation (3) come from the 2D boson density above Ec and the small 3D contribution below Ec, respectively. In Fig. 3a, we overlay equation (3) with D = √3/2πJ, J = 5 K and Ec = 0.2 mK (= 2J⊥ for J⊥/J = 2 × 10−5) as a solid line. The predicted <nc> and TBEC reasonably reproduce the experimentally observed Tc and <nc> (arrows in Fig. 3a). This close agreement clearly indicates that the magnetic ordering near the QCP is described as a BEC stabilized by a very small interlayer coupling J⊥ of the order of 10−5J. The extremely small J⊥ compared to J implies that YbCl3 is very close to the 2D limit. We note that the estimate of interlayer coupling is fully consistent with that in a previous neutron-scattering study28.
At the BEC, the chemical potential μeff = gμB(Hs − H) − 2Ueff<nc> = 0. This gives an estimate of the effective interaction Ueff = gμB(Hs − H)/2<nc> for H < Hs, which is plotted as a function of <nc> in Fig. 3d. With <nc> → 0, Ueff only weakly decreases to Ueff ≈ 0.2J, which is estimated from the analysis of a 2D quantum critical Bose gas at H = Hs. The decrease can be fitted reasonably by Ueff = −U0(1/ln<nc> + 1/ln(J⊥/J)) with U0 = 6 K = 1.2J and J⊥/J = 2 × 10−5 with 2D logarithmic renormalization and 3D cut-off, as seen by the dotted line in Fig. 3d. U0 is smaller than but reasonably close to the Ueff = 3–5J estimated for the canonical 3D BEC systems. Note that Ueff = −U0/ln<nc> goes to 0 with <nc> → 0 but stays a finite Ueff of ~0.2J at <nc> ≈ 0, which we discussed as a cut-off by the interlayer coupling J⊥. These observations firmly establish the presence of 2D logarithmic renormalization, one of the hallmarks of 2D physics.
Thermal fluctuations in the 2D limit
Reflecting the proximity of the system to the 2D limit, clear signatures of 2D thermal fluctuations are observed above Tc in the specific heat data. In the specific heat power α(T) map in Fig. 1c, the red region of 2D quantum critical behaviour with α ≈ 1 crosses over to a white region with α < 1 with lowering temperature. The white area that extends down to Tc corresponds to the accelerated increase of C(T)/T from a T-independent behaviour upon approaching Tc in Fig. 2b, which marks the region of thermal fluctuations. It spreads over a wide range of temperatures, from as high as ~2Tc (dotted line in Fig. 1c) down to Tc, which points to the 2D character of the thermal fluctuations. Below Tc, we see a decrease of C(T)/T and a corresponding positive power α that decreases eventually to ~2. As the lowest temperature ~100 mK is still higher than 0.5Tc in the critical region near Hs (>5.5T), it is difficult to extract the low-T limit of α and to discuss the dimensionality of fluctuations below Tc.
Because the system is essentially an XY magnet near the QCP and in the 2D limit, the 2D fluctuations observed above and below Tc may carry certain characteristics of a BKT transition for the strictly 2D case. It is tempting to infer here that the hypothetical BKT transition temperature TBKT in the J⊥ = 0 limit is very likely close to the observed BEC transition temperature Tc. Theoretically, it was shown for classical spins that the long-range ordering temperature Tc for a small J⊥ is only slightly above TBKT (ref. 38). QMC simulations of a S = 1/2 Heisenberg antiferromagnet on a purely 2D square lattice (not honeycomb lattice) under magnetic fields near the saturation field Hs (ref. 39) give an estimate of the BKT transition temperature TBKT/J ≈ 1 − H/Hs, which is indeed reasonably close to the experimentally observed BEC transition temperatures Tc in Fig. 1c.
Highly mobile nature of 2D Bose gas at the QCP
The interacting 2D Bose gas at the QCP is highly mobile at low temperatures, very likely due to the reduced boson–boson interactions in the dilute and 2D limit, which shows up as a singular enhancement of thermal conductivity κ(T) at Hs. Figure 4a shows the temperature dependence of κ/T. At the highest measured field of 11.9 T, the heat flow carried by magnetic excitations and the scattering of phonons by magnetic excitations are negligibly small below 2 K, as the gap for magnetic excitations is well developed (»2 K in Fig. 1c). κ(T) at 11.9 T is therefore a reference for the maximum phonon thermal conductivity in the absence of scattering by magnetic excitations. κ(T) at high temperatures above ~0.6 K decreases monotonically with lowering H from 11.9 T, reflecting the phonon-dominated thermal transport in the corresponding temperature range and the increase of magnetic excitations to scatter phonons due to the suppression of the magnetic excitation gap. At lower temperatures below ~0.5 K, κ(T) is larger than that at 11.9 T, the maximum phonon thermal conductivity, which indicates the presence of additional contributions other than the phonon contribution, naturally those from magnetic excitations. We plot the normalized differential thermal conductivity ∆κ/κ(11.9 T) ≡ [κ(T, H) − κ(T, 11.9 T)]/κ(T, 11.9 T) as a colour contour map on the H–T phase diagram in Fig. 4b, where the positive contribution indicates the excess thermal conductivity originating from the magnetic heat carriers. A singular positive ∆κ emerges up to ~0.5 K as a vertical red spike with a width of ~0.4 T around Hs in Fig. 4b, indicating that the magnetic contribution of thermal conductivity at low temperatures peaks sharply at Hs independent of T. This can be confirmed in the isotherm in Fig. 4c.
a, Thermal conductivity κ/T as a function of temperature T under magnetic fields up to 11.9 T. b, The normalized excess thermal conductivity ∆κ(H)/κ(11.9 T) = [κ(T, H) − κ(T, 11.9 T)]/κ(T, 11.9 T) plotted as a colour map on the magnetic field H and the temperature T plane. The excess conductivity ∆κ(H) = κ(H) − κ(11.9 T) is the deviation from κ(T) at 11.9 T. κ(11.9 T) data can be regarded as a phonon-only contribution to κ in the absence of scattering by magnetic excitations. c, The H-dependence of ∆κ(H)/κ(11.9 T) at 0.2, 0.4 and 1.5 K. d, The H-dependence of C(H)/T at 0.2 and 0.4 K.
The thermal conductivity of 2D magnetic excitations is expressed as κmag = (1/2)Cmag<vmag>lmag, where Cmag, vmag and lmag are the specific heat, the velocity and the mean free path of magnetic excitations, respectively. Cmag(H) ≈ C(H) at low temperatures shows a peak at the magnetic transition field Hc(T), as in Fig. 4d, which moves away to a lower field from Hs with increasing T and is distinct from the position of the ∆κ peak always at Hs. The singular enhancement of magnetic thermal conductivity ∆κ should therefore be dominated by the enhancement of <vmag>lmag at Hs. As <vmag> ≈ √2mkBT (m, boson mass) does not strongly depend on H around Hs, lmag(H) must be enhanced drastically in a very narrow field region near the QCP. At T = 0.2 K, the peak value ∆κ/T ≈ 0.13 W K−2 m−1 at H = Hs represents a lower bound for the magnetic contribution κmag/T, as the phonon contribution κph(T) should be suppressed from the maximum phonon contribution κ(T, 11.9 T) in the presence of scattering by magnetic excitations. We estimate a thermal velocity <vmag> of 62 m s−1 using a boson mass of 1,570 me at the bottom of the honeycomb tight-binding band with a hopping t = J/2 = 2.5 K. From ∆κT−1 and <vmag> together with Cmag/T ≈ C/T = 1 J mol−1 K−2 at H = Hs, we estimate a lower bound for the mean free path of 2D quantum critical bosons as long as lmag ≈ 0.3 μm, which indicates the highly mobile nature of 2D bosons. We were not able to conduct a more detailed and deeper analysis of κmag(T) and lmag(T) because of the difficulty in estimating quantitatively the suppressed phonon contribution κph(T) in the presence of magnetic excitations (see Supplementary Information for further details). We note that in the red-spike region of the rapid enhancement of ∆κ in Fig. 4b, the number of bosons <n> is less than 0.1. We argue that the low boson density <n> around Hs reduces the dominant boson–boson scattering represented by 2Ueff<n> and makes the quantum critical 2D Bose gas highly mobile, which drastically enhances ∆κ. The 2D logarithmic suppression of boson–boson scattering Ueff may further enhance ∆κ around the QCP. An increase of κ around a QCP was also observed in the 3D magnetic BEC system, NiCl2-4SC(NH2)2, at very low temperatures40. The κ peak as a function H around the QCP, however, is appreciably broader than the present 2D case, if normalized by the field scale of Hs, and appears to be closely correlated with the C(H) peak in contrast to the present 2D case. In this 3D analogue, the dominant scattering of bosons is indeed ascribed to static defects (disorder)40 rather than boson–boson interactions in the temperature range of investigation.
In summary, we identified a 2D-limit BEC quantum criticality in the honeycomb quasi-2D Heisenberg antiferromagnet YbCl3 under magnetic fields around the saturation field Hs, where a magnetic-field-induced quantum phase transition to the FP state takes place. At Hs, the QCP, the system behaves as a highly mobile dilute 2D gas of bosons in the density <n> = 0 limit, with the critical exponents of specific heat C(T) and magnetization M(T) predicted for the BEC-QCP in the 2D limit. Lowering the magnetic field to H < Hs, an extremely weak interlayer coupling J⊥ ≈ 10−5J marginally stabilizes a 3D LRO below Tc, which can de described quantitatively as a BEC. Reflecting the 2D-limit nature, 2D quantum and thermal fluctuations are captured clearly above Tc. A small boson–boson interaction Ueff of ~0.2J, one order of magnitude smaller than those in 3D analogues, is observed at the QCP, which increases only weakly with lowering H from the QCP, namely boson doping. The drastic suppression and the weak H-dependence can be quantitatively described as the logarithmic renormalization of the bare boson–boson interaction unique to 2D. YbCl3 is an ideal arena to explore the physics of 2D interacting hard-core bosons.
Methods
Single crystals
Single-crystalline samples of YbCl3 used in this study, transparent and with a thin plate-like shape, were synthesized by a self-chemical-vapour-transport method. Polycrystalline anhydrous YbCl3 (Sigma-Aldrich 99.99%) was used as a starting material and sealed under vacuum in a long quartz tube with inner diameter of 15 mm. The starting material was placed at the hot end of the tube, which was heated to 900 °C and subsequently cooled down to 750 °C at a rate of 1 °C per hour. The temperature difference between the hot and the cold ends of tube was approximately 100 °C during the growth. The negligibly small paramagnetic responses from the impurities in M and the large boundary-limited κ confirm the high quality of the single crystals. The crystallographic axis was checked by single-crystal X-ray diffraction. The magnetic field was applied always along the in-plane a-axis.
Magnetization measurements
The magnetization M below 3 K was measured with a homemade Faraday magnetometer installed in a 3He–4He dilution refrigerator. The measurements were conducted on a few pieces of crystals put together, aligned in the same direction, with a total mass of ∼0.7 mg. These were covered with dried Apiezon-N grease to protect the crystals from oxidation. The oxidation of samples could be checked by the presence of a paramagnetic response in the magnetization curve. We used data only from crystals with negligibly small traces of such response. The absolute value of M was determined by calibrating the magnitude of the field-dependent Faraday signals at 2 K with previous data taken at 1.8 K (ref. 30). The 0.2 K difference between the two measurements gives an error in the calibration up to ∼1%, which does not influence the conclusion of this work. We further checked that the calibrated data are consistent with those measured at high temperatures T ≥ 2 K by a commercial setup (Quantum Design Physical Property Measurement System, Vibrating Sample Magnetometer option).
Specific heat measurements
The specific heat C was measured by a relaxation calorimetry42 for aligned crystals with a total mass of ∼0.07 mg, which were covered with Apiezon-N grease to avoid oxidation. The total mass was determined by matching the C of single crystals with that of a polycrystalline sample at zero field and below ∼1 K, where the contribution from the grease can be reasonably neglected. The grease contribution was determined as a difference from the polycrystalline sample at higher T. This amounts to 15% of the total heat capacity at 2 K and shows roughly T2-dependence, which can be ascribed to the contribution from amorphous phonons of the grease. We subtracted this from all the data including those under fields.
Thermal conductivity measurements
κ was measured with a conventional steady-state method using a 3He–4He dilution refrigerator in a temperature range of 0.1–3 K. The sample with dimensions ∼1 mm × ∼2 mm × ∼20 µm thick was mounted onto a homemade cell. The cell was sealed in a glove box under argon atmosphere, which was then evacuated in the cryostat through a simple pop-up valve mechanism. Two more samples with similar dimensions were measured using a 3He cryostat, and the results were well reproduced in the T-range of overlap (0.3–3 K).
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request. Source data are provided with this paper.
References
Bose, S. N. Plancks gesetz und lichtquantenhypothese. Z. Phys. 26, 178–181 (1924).
Einstein, A. Quantentheorie des einatomigen idealen gases. Sitzungsber. Kgl. Preuss. Akad. Wiss., 261–267 (1924).
Zapf, V., Jaime, M. & Batista, C. D. Bose–Einstein condensation in quantum magnets. Rev. Mod. Phys. 86, 563–614 (2014).
Giamarchi, T., Rüegg, C. & Tchernyshyov, O. Bose–Einstein condensation in magnetic insulators. Nat. Phys. 4, 198–204 (2008).
Matsubara, T. & Matsuda, H. A lattice model of liquid helium, I. Prog. Theor. Phys. 16, 569–582 (1956).
Nikuni, T., Oshikawa, M., Oosawa, A. & Tanaka, H. Bose–Einstein condensation of dilute magnons in TlCuCl3. Phys. Rev. Lett. 84, 5868–5871 (2000).
Rüegg, C. et al. Bose–Einstein condensation of the triplet states in the magnetic insulator TlCuCl3. Nature 423, 62–65 (2003).
Jaime, M. et al. Magnetic-field-induced condensation of triplons in Han purple pigment BaCuSi2O6. Phys. Rev. Lett. 93, 087203 (2004).
Sebastian, S. E. et al. Dimensional reduction at a quantum critical point. Nature 441, 617–620 (2006).
Zapf, V. S. et al. Bose–Einstein condensation of S = 1 nickel spin degrees of freedom in NiCl2–4SC(NH2)2. Phys. Rev. Lett. 96, 077204 (2006).
Batyev, E. G. & Braginskii, L. S. Antiferromagnet in a strong magnetic field: analogy with Bose gas. Sov. Phys. JETP 60, 781–786 (1984).
Giamarchi, T. & Tsvelik, A. M. Coupled ladders in a magnetic field. Phys. Rev. B59, 11398–11407 (1999).
Mermin, N. D. & Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 17, 1133–1136 (1966).
Berezinskii, V. L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. II. Quantum systems. Sov. Phys. JETP 34, 610–616 (1972).
Kosterlitz, J. M. & Thouless, D. J. Long range order and metastability in two dimensional solids and superfluids. (Application of dislocation theory). J. Phys. C 5, L124–L126 (1972).
Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 6, 1181–1203 (1973).
Schick, M. Two-dimensional system of hard-core bosons. Phys. Rev. A 3, 1067–1073 (1971).
Rançon, A. & Dupuis, N. Kosterlitz–Thouless signatures in the low-temperature phase of layered three-dimensional systems. Phys. Rev. B 96, 214512 (2017).
Hirakawa, K. Kosterlitz–Thouless transition in two-dimensional planar ferromagnet K2CuF4 (invited). J. Appl. Phys. 53, 1893–1898 (1982).
Hemmida, M., Krug von Nidda, H.-A., Tsurkan, V. & Loidl, A. Berezinskii–Kosterlitz–Thouless type scenario in the molecular spin liquid ACr2O4(A =Mg, Zn, Cd). Phys. Rev. B 95, 224101 (2017).
Heinrich, M., Krug von Nidda, H.-A., Loidl, A., Rogado, N. & Cava, R. J. Potential signature of a Kosterlitz–Thouless transition in BaNi2V2O8. Phys. Rev. Lett. 91, 137601 (2003).
Tutsch, U. et al. Evidence of a field-induced Berezinskii–Kosterlitz–Thouless scenario in a two- dimensional spin–dimer system. Nat. Commun. 5, 5169 (2014).
Fisher, D. S. & Hohenberg, P. C. Dilute Bose gas in two dimensions. Phys. Rev. B 37, 4936–4943 (1988).
Allenspach, S. et al. Multiple magnetic bilayers and unconventional criticality without frustration in BaCuSi2O6. Phys. Rev. Lett. 124, 177205 (2020).
Weickert, F. et al. Low-temperature thermodynamic properties near the field-induced quantum critical point in NiCl2-4SC(NH2)2. Phys. Rev. B 85, 184408 (2012).
Sala, G. et al. Crystal field splitting, local anisotropy, and low-energy excitations in the quantum magnet YbCl3. Phys. Rev. B 100, 180406 (2019).
Xing, J. et al. Néel-type antiferromagnetic order and magnetic field-temperature phase diagram in the spin-1/2 rare-earth honeycomb compound YbCl3. Phys. Rev. B 102, 014427 (2020).
Sala, G. et al. Van hove singularity in the magnon spectrum of the antiferromagnetic quantum honeycomb lattice. Nat. Commun. 12, 171 (2021).
Sala, G. et al. Field-tuned quantum renormalization of spin dynamics in the honeycomb lattice Heisenberg antiferromagnet YbCl3. Commun. Phys. 6, 234 (2023).
Hao, Y. et al. Field-tuned magnetic structure and phase diagram of the honeycomb magnet YbCl3. Sci. China Phys. Mech. Astron. 64, 237411 (2020).
Sengupta, P. et al. Nonmonotonic field dependence of the Néel temperature in the quasi-two-dimensional magnet [Cu(HF2)(pyz)2]BF4. Phys. Rev. B 79, 060409(R) (2009).
Hijmans, J. P. A. M., Kopinga, K., Boersma, F. & de Jonge, W. J. M. Phase diagrams of pseudo one-dimensional Heisenberg systems. Phys. Rev. Lett. 40, 1108–1111 (1978).
Popov, V. N. On the theory of the superfluidity of two- and one-dimensional Bose systems. Theor. Math. Phys. 11, 565–573 (1972).
Popov, V. N. Functional Integrals in Quantum Field Theory and Statistical Physics (Reidel, 1983).
Yamada, F. et al. Magnetic-field induced Bose–Einstein condensation of magnons and critical behavior in interacting spin dimer system TlCuCl3. J. Phys. Soc. Jpn. 77, 013701 (2008).
Matsumoto, M., Normand, B., Rice, T. M. & Sigrist, M. Magnon dispersion in the field-induced magnetically ordered phase of TlCuCl3. Phys. Rev. Lett. 89, 077203 (2002).
Paduan-Filho, A. et al. Critical behavior of the magnetization in the spin-gapped system NiCl2–4SC(NH2)2. J. Appl. Phys. 105, 07D501 (2009).
Hikami, S. & Tsuneto, T. Phase transition of quasi-two dimensional planar system. Prog. Theor. Phys. 63, 387–401 (1980).
Cuccoli, A., Roscilde, T., Vaia, R. & Verrucchi, P. Field-induced XY behavior in the S = 1/2 antiferromagnet on the square lattice. Phys. Rev. B 68, 060402(R) (2003).
Kohama, Y. et al. Thermal transport and strong mass renormalization in NiCl2-4SC(NH2)2. Phys. Rev. Lett. 106, 037203 (2011).
Momma, K. & Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Matsumoto, Y. & Nakatsuji, S. Relaxation calorimetry at very low temperatures for systems with internal relaxation. Rev. Sci. Instrum. 89, 033908 (2018).
Acknowledgements
We acknowledge C. D. Batista, Y. Kato and D. Huang for stimulating discussions and K. Pflaum and M. Dueller for experimental support. This work was partly supported by the Alexander von Humboldt Foundation and the Japan Society for the Promotion of Science KAKAENHI (grant nos. JP22H01180 and JP17H01140) and by the Max-Planck-UBC-UTokyo Center for Quantum Materials and the Deutsche Forschungsgemeinschaft (German Research Foundation) – TRR 360 – 492547816.
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
Y.M., K.K. and H.T. conceived the research. K.K. synthesized the single crystals. Y.M. performed the magnetization and specific heat measurements. J.A.N.B., S.S. and Y.M. performed the thermal conductivity measurements. J.N. performed the structural characterization of crystals. Y.M., J.A.N.B. and H.T. analysed the data. G.J. and H.T. provided theoretical inputs. P.R. and G.J. verified the analysis. Y.M. and H.T. wrote the paper with inputs from all the authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Adam Aczel, Marcelo Jaime and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary texts and Figs. 1–8.
Source data
Source Data Fig. 1
Statistical source data.
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Matsumoto, Y., Schnierer, S., Bruin, J.A.N. et al. A quantum critical Bose gas of magnons in the quasi-two-dimensional antiferromagnet YbCl3 under magnetic fields. Nat. Phys. 20, 1131–1138 (2024). https://doi.org/10.1038/s41567-024-02498-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-024-02498-w