Demonstration and imaging of cryogenic magneto-thermoelectric cooling in a van der Waals semimetal

Abstract

Attaining viable thermoelectric cooling at cryogenic temperatures is of considerable fundamental and technological interest for electronics and quantum materials applications. In-device temperature control can provide more efficient and precise thermal environment management compared with conventional global cooling. The application of a current and perpendicular magnetic field gives rise to cooling by generating electron–hole pairs on one side of the sample and to heating due to their recombination on the opposite side, which is known as the Ettingshausen effect. Here we develop nanoscale cryogenic imaging of the magneto-thermoelectric effect and demonstrate absolute cooling and an Ettingshausen effect in exfoliated WTe₂ Weyl semimetal flakes at liquid He temperatures. In contrast to bulk materials, the cooling is non-monotonic with respect to the magnetic field and device size. Our model of magneto-thermoelectricity in mesoscopic semimetal devices shows that the cooling efficiency and the induced temperature profiles are governed by the interplay between sample geometry, electron–hole recombination length, magnetic field, and flake and substrate heat conductivities. The observations open the way for the direct integration of microscopic thermoelectric cooling and for temperature landscape engineering in van der Waals devices.

Main

Thermoelectric effects have long been used for generating power, cooling electronic devices and measuring temperature where compact size, high stability, vibrationless operation without moving parts and high tunability are required^1,2. Historically, research efforts have focused on elevated temperatures as the cooling efficiency decreases substantially at lower temperatures, such that it is eventually overshadowed by Joule heating for realistic current strengths. In recent years, the advent of high-purity single-crystal semimetals has led to increased interest in thermoelectric effects at cryogenic temperatures^{3,4,5,6,7,8,9,10,11,12}.

The common approach to thermoelectric cooling is based on the Peltier effect¹³, in which a temperature gradient is attained along the current flow direction in structures composed of regions or materials with different Peltier coefficients, which, thus, carry different average amounts of heat per transferred unit charge. Peltier cooling of bulk materials down to liquid nitrogen temperatures has been realized in a number of studies^2,14, with only one report of bulk cooling at liquid He temperatures¹⁵. By engineering microscopic devices that form energy gaps in the electron density of states, like superconducting junctions or quantum dots, the efficiency of Peltier cooling at very low temperatures can be enhanced substantially due to the preferential transmission of electrons at specific energies^16,17,18.

Here we address a very different and interesting magneto-electro-thermal mechanism, the Ettingshausen effect¹⁹, which has not been studied in microscopic devices previously¹⁸, and we present the observation of the Ettingshausen effect and Ettingshausen cooling at 4 K. The application of a charge current in the presence of a perpendicular magnetic field leads to a temperature gradient that is transverse to the current flow direction, rather than along it. In a metal, this effect is due to the energy dependence of the drift velocity of the charge carriers, which in the presence of magnetic field, deflects the high- and low-energy carriers to opposite sides of the sample, thus providing heating and cooling upon equilibration of the carriers with the lattice (Fig. 1a). The resulting current to temperature gradient conversion in this case is rather weak.

Fig. 1: Thermal imaging of the Ettingshausen effect in a WTe₂ flake at 4.3 K.

a,b, Schematics of the Ettingshausen effect in metals (a) and in compensated semiconductors or semimetals (b) in the presence of a perpendicular magnetic field B. In a metal, the average Lorentz force F_L is counterbalanced by the transverse electrostatic force F_E of the Hall voltage. As the higher energy electrons usually have a lower drift velocity and, hence, lower F_L, a small transverse thermoelectric effect develops. In semiconductors and semimetals, a much larger transverse temperature gradient of opposite sign is induced by electron–hole pair generation at the cold edge and recombination at the hot edge. c, Optical image of a WTe₂ device showing three rectangular chambers (grey) of widths of W = 10, 20 and 5 µm along with surrounding additional patterns. A sinusoidal a.c. current I at frequency f is applied in series (white arrow) through the Au contacts (yellow). The dashed white rectangle marks the scan window in d–i. d–f, Temperature maps ${\updelta T}_\mathrm{J}(x,y)$ corresponding to Joule heating acquired at 2f with I = 5 µA at magnetic fields of B = 0 T (d), 1.04 T (e) and 5 T (f). g–i, Corresponding maps of Ettingshausen temperature component ${\updelta T}_\mathrm{E}(x,y)$ acquired simultaneously at f at magnetic fields of B = 0 T (g), 1.04 T (h) and 5 T (i). j, Left axis: temperature difference between the hot and cold edges ΔT_E (blue dots) versus I with a linear fit (blue line) at B = 5 T. Right axis: ${\updelta T}_\mathrm{J}({0,0})$ at the centre of the chamber versus I (red dots) and a parabolic fit (red line). k, Magnetic field dependence of δT_J at I = 50 µA. l, ΔT_E versus B in the three adjacent chambers of W = 5, 10 and 20 µm at I = 50 µA (dots) showing nonlinear dependence on B and non-monotonic dependence on W. The solid curves are the corresponding ΔT_E from the numerical simulations.

Source data

A much stronger effect can be attained in semiconductors and semimetals hosting both electrons and holes with approximately equal densities and mobilities^18,20. Under such circumstances, the Hall voltage that usually develops across a device is diminished and the unbalanced Lorentz force drives both the electrons and holes in the same transverse direction (Fig. 1b). This leads to a non-equilibrium electron–hole pair accumulation on one side and depletion on the opposite side. As a result, recombination and generation of electron–hole pairs is increased, thus providing heating and cooling at opposing sides through equilibration with the lattice¹⁹. As such, heating and cooling are expected to be constrained to a small area within the recombination length l_R from the boundaries. Hence, a thermal measurement technique with spatial resolution on that length scale is required to fully elucidate the effect.

The search for suitable materials for thermoelectric cooling has focused predominantly on bulk systems, leaving the unrecognized potential of mesoscopic devices for integrated cooling largely unexplored¹⁸. Employing van der Waals (vdW) semimetals as thermoelectric elements^{21,22,23,24,25,26} is especially promising since they can be readily integrated into stacks of atomic layers and moiré heterostructures^27,28. Herein, different materials, such as insulating, semiconducting, superconducting or magnetic layers, in the heterostructure can fulfil different functionalities. Accordingly, we propose the use of a vdW semimetal as an active thermoelectric element for in-device cooling or for engineering a controllable temperature gradient within a device. A particularly promising vdW material for thermoelectric cooling is the Weyl semimetal WTe₂ because of its very high charge carrier mobility and near compensation of electron and hole densities^29,30,31. In its bulk form, it has already been shown to display a large Nernst effect³² and ultrahigh Ettingshausen effect at temperatures above 20 K (ref. ¹²).

Thermoelectric mechanisms in which out-of-equilibrium voltages or currents are generated by temperature gradients, like the Seebeck and Nernst effects, have been investigated extensively in microscopic vdW devices. These studies are typically performed by measuring voltages across microscopic contacts induced by global temperature gradients^{21,22,23,24,25,26,33,34,35} or by local heating using, for example, a scanning focused laser beam^{36,37,38,39,40,41,42,43,44,45}. In contrast, electro-thermal processes, like the Peltier and Ettingshausen effects, for which temperature gradients need to be measured or imaged in response to applied currents, are much more challenging to investigate in microscopic devices and have, thus far, been restricted to above liquid nitrogen temperatures^46,47. In this work, we provide thermal imaging of magneto-electro-thermal cooling at liquid He temperatures in exfoliated flakes of the transition metal dichalcogenide WTe₂, revealing an ultrahigh Ettingshausen effect and the underlying mesoscopic mechanisms that have been inaccessible experimentally hitherto.

Cryogenic thermal imaging

A superconducting quantum interference device on a tip (SQUID-on-tip, SOT)⁴⁸ made of MoRe (ref. ⁴⁹) with a diameter of 110 nm was scanned above the sample surface at a height h ≈ 80 nm in an He exchange gas atmosphere. It was employed as a nanothermometer⁵⁰ with 2.6 µK Hz^−1/2 sensitivity at T₀ = 4.3 K, operating in an applied out-of-plane magnetic field of up to B = 5 T (Methods), as shown schematically in Fig. 1b. A high-quality WTe₂ single crystal³¹ was exfoliated to produce a d = 269 nm thick flake and patterned by reactive ion etching (Methods) into a number of rectangular chambers with different widths W (Fig. 1c). To circumvent the 1/f noise of the SOT, a sine or square-wave a.c. current at frequency f = 85.37 Hz and variable rms amplitude I was applied to the three chambers, which were connected in series by narrow constrictions (Fig. 1c). The resulting a.c. change in the local temperature δT(x,y) relative to the base temperature T₀ was imaged by the scanning SOT.

Imaging the Ettingshausen effect in WTe₂

The current-induced change in the local temperature δT has two contributions, one arising from Joule heating δT_J and the other from the Ettingshausen effect δT_E. By applying a sine-wave a.c. current through the sample, we can image these two contributions independently as follows. Since the Ettingshausen effect is linear in I, δT_E is a sine-wave temperature modulation at the frequency f of the applied current. We, thus, detect this contribution by lock-in measurement at the fundamental frequency f. In contrast, Joule heating is quadratic in I and, therefore, results in d.c. heating superimposed by an a.c. temperature modulation at frequency 2f (Methods). We image this a.c. δT_J modulation by lock-in detection at the second harmonic.

Figure 1d–f shows the Joule heating $\updelta {T}_{{\rm{J}}}(x,y)$ induced in the largest chamber (dashed rectangle in Fig. 1c) at B = 0, 1.04 and 5 T, respectively, at I = 50 μA (thermal images of the two smaller chambers of the device are shown in Extended Data Fig. 3). δT_J was rather uniform in most of the chamber area with intense hot spots at the constrictions where the current density is high. Figure 1j shows that δT_J in the chamber grew quadratically with I, as expected for Joule heating. δT_J increased by over two orders of magnitude with the field, growing approximately quadratically with B, as shown in Fig. 1k. This is the consequence of the very large magnetoresistance ${\rho }_{{xx}}(B)\propto {B}^{2}$ in high-purity WTe₂, as reported previously^{29,30,31,32,51}.

The Ettingshausen temperature distribution $\updelta {T}_{{\mathrm{E}}(x,y)}$ is shown in Fig. 1g–i. At zero field, δT_E = 0 as expected (the weak signal in the constrictions is an artefact; Methods). Upon increasing the field, a large temperature gradient developed transverse to the current and magnetic field directions. The temperature difference ${\Delta}{T}_{\mathrm{E}}={\updelta}{T}_{\mathrm{E}}\left(0,-{W}/{2}\right)-{\updelta}{T}_{\mathrm{E}}\left(0,{W}/{2}\right)$ between the hot (bottom) and the cold (top) edges at $y=\mp W/2$ across the sample centre (x = 0) grew linearly with I (Fig. 1j), as expected for the Ettingshausen effect, ${\Delta T}_\mathrm{E}={P}_\mathrm{E}{IB}/W$, where P_E is the Ettingshausen coefficient. For B = 5 T and W = 20 μm, we found an ultrahigh Ettingshausen signal ${\Delta}{T}_{\mathrm{E}}/(JW)=2.2\times {10}^{-5}\,{\mathrm{K}}\,{\mathrm{A}}^{-1}\,{\mathrm{m}}$(J is the current density) comparable to the previously reported bulk values¹² but at a much lower temperature. However, in contrast to the standard bulk behaviour, we found that ΔT_E is not linear in B, as shown in Fig. 1l. Even more surprisingly, investigating chambers with different widths revealed a non-monotonic W dependence, with the chamber with W = 10 μm showing a larger ΔT_E than those with W = 20 μm or W = 5 μm (Fig. 1l). Moreover, Fig. 1h,i shows a non-trivial spatial distribution of ${\updelta}{T}_{\mathrm{E}}(x,y)$ with enhanced heating and cooling signals on the left and right edges near the constrictions. These features were also observed in additional samples, as shown in Extended Data Figs. 2–4.

Absolute cooling

The linear increase of the Ettingshausen temperature difference ΔT_E with current does not necessarily mean that the temperature of the cold edge of the sample decreases monotonically with I or that real cooling has been achieved at the cold edge. This is because the Joule heating usually has a dominant contribution. The first and second harmonic a.c. temperature variations in response to a sine-wave a.c. current presented in Fig. 1 allowed us to distinguish between the Ettingshausen and Joule terms, but these terms do not include the d.c. Joule heating component (Methods). To map the actual map of excess temperature, we modulated the applied current between zero and I by applying a unipolar square wave. In this case, the measured a.c. δT(x, y) provides an image of the total current-induced excess temperature, which is the difference between the local temperature $T(x,y)={T}_{0}+{{\updelta}}T(x,y)$ in the presence of the current and the base temperature T₀ in its absence. Positive δT represents heating whereas negative δT is cooling to below T₀.

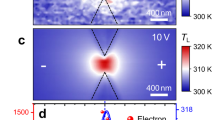
Figure 2a shows the resulting temperature map δT(x, y) in the W = 20 µm chamber at B = 0.64 T and I = 25 µA. δT(x, y) along the top edge of the sample is negative. That is, the local temperature in the presence of the current is below T₀, revealing current-induced absolute cooling. Even stronger cooling is observed in the top two corners of the chamber. To the best of our knowledge, this is the first observation of Ettingshausen cooling at liquid He temperatures.

Fig. 2: Absolute cooling.

a, Map of the current-induced local excess temperature $\updelta T(x,y)$ relative to the base temperature T₀ = 4.3 K, generated by a unipolar square-wave current excitation of I = 25 µA in the WTe₂ device at B = 0.64 T. Regions with negative δT are cooled by the current to below T₀. b, Profiles of excess temperature $\updelta T(0,y)$ along the black dashed line in a at various applied currents. c, Simulated temperature profiles $\updelta T(0,y)$. d, Excess temperature at the cold edge of the chamber $\updelta {T}_{\mathrm{cold}}$ versus I at different magnetic fields showing absolute cooling $\updelta {T}_{\mathrm{cold}} < 0$. e, Measured ${\updelta T}_{\mathrm{cold}}(I,B)$ diagram showing the parameter space of absolute cooling (blue). f, Simulated ${\updelta T}_{\mathrm{cold}}(I,B)$ diagram. The colour in the high-temperature regions (red) in e and f is saturated for clarity. The dashed lines in e and f show the fit of the current ${I}_{0}\left(B\right)$ from equation (6) below which absolute cooling occurs.

Source data

Next, we explored the current and field dependence of the cooling mechanism. Figure 2b shows the temperature profile δT(0, y) across the sample centre (dashed line in Fig. 2a) at B = 0.64 T and various applied currents I. The temperature at the hot edge ($y=-W/2$) increased monotonically with the current, and the temperature difference ΔT_E between the hot and cold edges increased linearly with I (Fig. 1j). Yet, the temperature at the cold edge ($y=W/2$) showed non-monotonic behaviour due to competition between the linear Ettingshausen cooling and the quadratic Joule heating. As a result, absolute cooling (δT < 0) was achieved only at low currents. Note that at any current, the temperature at the cold edge was lower than the temperature at the hot edge or in the sample centre. That is, the relative Ettingshausen cooling always occurred, but at high currents it could not overcome the Joule heating to attain absolute cooling.

The cooling mechanism was also non-monotonic in magnetic field. Figure 2d shows $\updelta {T}_{\mathrm{cold}}=\updelta T(0,W/2)$ versus I at different B. At B = 0, the excess temperature was always positive, increasing monotonically with I. At finite fields, δT_cold was negative at low currents, initially showing a negative slope with I, which increased monotonically with B. The current at which the maximal negative temperature ${\updelta T}_{\mathrm{cold}}^{\max }(B)$ is attained decreased monotonically with B, but $\updelta {T}_{\,{\mathrm{cold}}}^{\,\max }\left(B\right)$ has a non-monotonic B dependence with maximal negative ${\updelta T}_{\mathrm{cold}}^{\max }$ attained at B ≈ 2 T. Figure 2e shows the full map of $\updelta {T}_{\mathrm{cold}}(B,I\;)$, revealing a wide range of fields and currents at which negative excess temperatures can be achieved (blue).

Theory of Ettingshausen effect in mesoscopic devices

The mechanism underlying the large Ettingshausen effect in WTe₂ stems from the near compensation of electron and hole densities, ${n}_\mathrm{e}\approx{n}_\mathrm{h}=n$, and their mobilities, ${\mu}_\mathrm{e}\approx{\mu}_\mathrm{h}=\mu$. In bulk devices, the induced transverse temperature difference ${\Delta T}_\mathrm{E}={P}_\mathrm{E}{IB}/W$ is proportional to B/W (refs. ^12,19,20). This relation does not hold in mesoscopic devices because of the competition between different microscopic length scales and due to the inherently non-uniform current distribution. Consider a bulk sample with uniform applied longitudinal electric field ${\mathbf{E}}={E}_{x}\hat{x}$. At B = 0 T, the resulting current density J comprises counterflowing particle flux densities of electrons j_e and holes j_h, ${\mathbf{J}}=e({{\mathbf{j}}}_{\mathrm{h}}-{{\mathbf{j}}}_{\mathrm{e}})$, where e is the elementary charge. An out-of-plane magnetic field ${\mathbf{B}}=B\hat{z}$ gives rise to a transverse Lorentz force F_L, which for a single-charge-type conductor is counterbalanced by the electrostatic force of the induced Hall voltage F_E, resulting in the absence of magnetoresistance (Fig. 1a). In a compensated semimetal, in contrast, the Hall voltage vanishes and F_L, which scales as μB, drives both the electrons and holes in the same transverse direction (Fig. 1b). This transverse flow of quasiparticles creates the quasiparticle current density ${\mathbf{P}}=e({{\mathbf{j}}}_{\mathrm{h}}+{{\mathbf{j}}}_{\mathrm{e}})$, which in turn causes a longitudinal Lorentz force that counteracts the force of the applied electric field, resulting in bulk magnetoresistance that scales as (μB)², ${\rho }_{{xx}}\cong {{\rho }_{0}(1+\mu }^{2}{B}^{2})$, where ρ₀ is the zero-field resistivity^{29,30,31,32,51}.

The edges play a crucial role in a microscopic device. In particular, the boundary conditions preclude a transverse particle flow at the sample edges. This implies that the magnetoresistance, which is caused by the transverse flow, is suppressed near the boundaries. A recent theoretical study^52,53 showed that the resulting current distribution across the width $-W/2\le y\le W/2$ of a long narrow strip is given by

$${J}_{x}\left(\,y\right)=\frac{{E}_{x}}{{{\rho }_{0}}(1+{\mu}^{2}{B}^{2})}\left[1+{\mu }^{2}{B}^{2}\frac{\cosh \left(2y/l_{\mathrm{R}}\right)}{\cosh \left(W/l_{\mathrm{R}}\right)}\right],$$

(1)

where ${l}_\mathrm{R}={l}_\mathrm{R}^{0}/\sqrt{1+{\mu }^{2}{B}^{2}}$ and ${l}_\mathrm{R}^{0}$ is the electron–hole recombination length at zero field. For ${l}_\mathrm{R}\ll W$, equation (1) shows that in the centre of the strip, the current density is suppressed by the magnetoresistance just like in the bulk limit, ${J}_{x}(\left|\,y\right|\ll W\;)=\frac{{E}_{x}}{{\rho }_{0}\left(1+{\mu }^{2}{B}^{2}\right)}$. Remarkably, along the edges, the current experiences no magnetoresistance, ${J}_{x}\left(\left|\,y\right|={W}/{2}\right)={{E}_{x}}/{{\rho }_{0}}$, remaining at its zero-field value. As a result, the current distribution peaks along the edges within narrow channels with a characteristic width of l_R (narrow bright slivers along the top and bottom edges in Fig. 3a).

Fig. 3: Numerical simulations of the magneto-thermoelectric response.

a, Normalized current density distribution $\left|{{{\mathbf{J}}}}(x,y)\right|$ and streamlines at B = 0.64 T and I = 25 μA (J₀ = I/W). b, Quasiparticle current density $\left|{{{\mathbf{P}}}}(x,y)\right|$ with streamlines. c, Out-of-equilibrium quasiparticle density $\updelta {n}_\mathrm{q}(x,y)$. The colours are saturated for clarity. d, Power density generated by Joule heating ${\dot{Q}}_\mathrm{J}(x,y)$. e, Power density ${\dot{Q}}_\mathrm{E}(x,y)$ produced by generation and recombination of quasiparticles due to the Ettingshausen effect. f, Total power density $\dot{Q}={\dot{Q}}_\mathrm{J}+{\dot{Q}}_\mathrm{E}$. g, Excess temperature distribution δT_J caused by Joule heating. h, Excess temperature distribution δT_E caused by the Ettingshausen effect. i, Total excess temperature $\updelta T(x,y)$. See Methods for simulation parameters.

In contrast to the conservation of charge current $\nabla \cdot {{{\mathbf{J}}}}=0$, the quasiparticle current P is not conserved because electron–hole pairs can be generated and recombined. Hence $\nabla \cdot {{{\mathbf{P}}}}=-\updelta {n}_\mathrm{q}/{\tau }_\mathrm{R}$, where $\updelta {n}_\mathrm{q}=\updelta {n}_\mathrm{e}+\updelta {n}_\mathrm{h}$ is the quasiparticle excess density, δn_e and δn_h are the out-of-equilibrium electron and hole densities, and τ_R is the electron–hole recombination time. In the narrow strip geometry, the resulting quasiparticle current and density distributions are given by

$${P}_{y}\left(\,y\right)=-\frac{\mu B{E}_{x}}{{\rho }_{0}\left(1+{\mu }^{2}{B}^{2}\right)}\left[1-\frac{\cosh \left({2y}/{{l}_\mathrm{R}}\right)}{\cosh \left({W}/{{l}_\mathrm{R}}\right)}\right].$$

(2)

$$\updelta {n}_\mathrm{q}(\,y)=-\frac{2\mu B{E}_{x}}{{\rho }_{0}\left(1+{\mu }^{2}{B}^{2}\right)}\frac{{\tau }_\mathrm{R}}{{l}_\mathrm{R}}\frac{\sinh \left({2y}/{{l}_\mathrm{R}}\right)}{\cosh \left({W}/{{l}_\mathrm{R}}\right)}.$$

(3)

In the central part of the sample, δn_q is small because the quasiparticle thermal generation and recombination rates are approximately balanced, like in thermal equilibrium, and P_y is essentially constant, as shown in Fig. 3b,c. The transverse P_y driven by the Lorentz force gives rise to a sharp accumulation (depletion) of the quasiparticles within l_R from the bottom (top) edge. As a result, the electron–hole pair recombination rate is enhanced (suppressed) by $\updelta {n}_\mathrm{q}/{\tau }_\mathrm{R}$ at the bottom (top) edge, giving rise to heating by phonon emission (cooling by phonon absorption).

The thermoelectric effect can, thus, be derived by considering the two heat-generating terms $\dot{Q}={\dot{Q}}_\mathrm{J}+{\dot{Q}}_\mathrm{E}$, where ${\dot{Q}}_\mathrm{J}={{{\mathbf{J}}}}\cdot {{{\mathbf{E}}}}$ is the Joule term, ${\dot{Q}}_\mathrm{E}={\epsilon }_\mathrm{p}\updelta {n}_\mathrm{q}/{\tau }_\mathrm{R}=-{\epsilon }_\mathrm{p}\nabla \cdot {{{\mathbf{P}}}}$ is the Ettingshausen contribution and ϵ_p is the average phonon energy released (absorbed) by recombination (generation) of an electron–hole pair:

$${\dot{Q}}_\mathrm{J}(\,y)=\frac{{E}_{x}^{2}}{{\rho }_{0}\left(1+{\mu }^{2}{B}^{2}\right)}\left[1+{\mu }^{2}{B}^{2}\frac{\cosh \left({2y}/{{l}_\mathrm{R}}\right)}{\cosh \left({W}/{{l}_\mathrm{R}}\right)}\right],$$

(4)

$${\dot{Q}}_\mathrm{E}(\,y)=-\frac{2{\epsilon}_\mathrm{p}\mu B{E}_{x}}{e{\rho }_{0}{l}_\mathrm{R}^{0}\sqrt{1+{\mu }^{2}{B}^{2}}}\frac{\sinh ({2y}/{{l}_\mathrm{R}})}{\cosh({W}/{{l}_\mathrm{R}})}.$$

(5)

As expected, ${\dot{Q}}_\mathrm{J}$ is symmetric in y and quadratic in E_x and, hence, appears in the second harmonic for the a.c. current, whereas ${\dot{Q}}_\mathrm{E}$ is antisymmetric in y and linear in E_x, consistent with the experimental results in Fig. 1.

To attain a better understanding of the thermoelectricity in mesoscopic systems, we ran three-dimensional (3D) finite-element numerical simulations for our sample geometry (Methods). Figure 3a shows that a high current density J is present in the constrictions, whereas in the rectangular chamber, the current density peaks along the sample edges where the magnetoresistance is suppressed. The corresponding Joule dissipation ${\dot{Q}}_\mathrm{J}$ is highest in the constrictions (Fig. 3d) and is enhanced in the narrow slivers along the top and bottom edges in the chamber. The quasiparticle current density ${{{\mathbf{P}}}}(x,y)$ in Fig. 3b also shows a large enhancement in the constrictions. In the rectangular chamber, P flows mostly transverse to J and is largest in the central area. Note that |${{{\mathbf{P}}}}\approx\mu B\mathbf{J}$| is substantially larger than |${{{\mathbf{J}}}}$| for the presented case of μB = 1.6, which corresponds to our experimental values at B = 0.64 T. The excess quasiparticle density $\updelta {n}_\mathrm{q}(x,y)$ sharply peaks along the sample boundaries, including the left and right edges (Fig. 3c). As a result, the Ettingshausen dissipation ${\dot{Q}}_\mathrm{E}$ (Fig. 3e) shows pronounced cooling along the edges in the top half of the sample and heating along the bottom-half edges. Depending on the parameters, the total dissipation $\dot{Q}={\dot{Q}}_\mathrm{J}+{\dot{Q}}_\mathrm{E}$ can be either positive everywhere or negative (cooling) along the top boundaries, as shown in Fig. 3f.

By incorporating heat diffusion equations for WTe₂ and for the Si substrate into the numerical calculations (Methods), we can derive the corresponding δT_J, δT_E and the total δT distributions. Figure 3g–i shows that the calculated local temperatures follow the local $\dot{Q}$ maps in Fig. 3d–f, albeit broadened by the thermal heat conductivities in the flake and the substrate. In particular, the enhancement of ${\dot{Q}}_\mathrm{J}$ in the narrow slivers along the edges in Fig. 3d is completely broadened in the δT_J map in Fig. 3g. We attain very good agreement between the numerical simulations and the experimental data for the microscopic parameters ${l}_{\mathrm{R}}^{0}=0.5\,\upmu\rm{m}$, μ = 25,000 cm² V⁻¹ s⁻¹ and ϵ_p = 0.06 meV. The calculated temperature distributions shown in Fig. 3g–i match qualitatively very well the measured δT_J and δT_E maps in Fig. 1e,h and with the total δT distribution in Fig. 2a. Figure 2c shows the calculated $\updelta T(y)$ profiles across the width of the sample at various currents, which reproduce well the experimental behaviour. Moreover, the experimental phase diagram of the absolute cooling $\updelta {T}_{\mathrm{cold}}(I,B)$ in Fig. 2e is also well described by the model (Fig. 2f), showing the accessible range of absolute cooling and the optimal parameters for achieving the lowest temperatures in our device. Finally, the model also recovers the non-monotonic width dependence and the nonlinearity of $\Delta {T}_\mathrm{E}\left(B\right)$ in Fig. 1l (solid lines).

Analytical model

Further insight into the role of the different parameters in a mesoscopic device can be attained by considering a simplified model for the total heat fluxes. The lateral heat flux from the hot to the cold side of the device is governed by the in-plane total heat conductivity κ of WTe₂ with thickness d. Further, heat flows from the hot side of the device to the substrate and from the substrate to the cold part of the device. The flow of heat depends on the out-of-plane heat conductivity κ′ of the substrate, which has effective thickness d_s. In this geometry, we find (Methods) that the condition on the applied current for attaining a negative excess temperature at the cold edge is I < I₀, where

$${I}_{0}\approx\frac{{\epsilon }_\mathrm{p}}{e{\rho }_{0}}\frac{4\mu B}{(1+{\mu }^{2}{B}^{2})\left(1+{W}_{\;0}^{\;2}/{W}^{\;2}\right)}$$

(6)

and ${W}_{0}\approx\sqrt{8d{d}_\mathrm{s}\kappa /{\kappa }^{{\prime} }}$. The dashed curve in Fig. 2e shows that the fit of I₀(B) to the experimental data provides a very good description of the cooling regime. Note that from equation (6), the maximum of I₀(B) occurs at μB = 1, which allows a direct evaluation of μ ≈ 23,000 cm² V⁻¹ s⁻¹ from the experimental data, consistent with the more accurate 3D simulations, resulting in μ = 25,000 cm² V⁻¹ s⁻¹.

By integrating ${\dot{Q}}_\mathrm{E}$ over the cold side of the sample and taking into account the above heat conductivities, we derive the transverse temperature difference (Methods):

$$\Delta {T}_\mathrm{E}\approx\frac{{{\epsilon }}_\mathrm{p}I}{ed\kappa }\frac{2\mu B}{(1+{\mu B{l}_\mathrm{R}^{0}}/{W}\,)\left(1+{{W}^{\,2}}/{{W}_{0}^{\,2}}\right)}.$$

(7)

This result emphasizes a number of key aspects of the mesoscopic nature of the Ettingshausen effect, which cannot be observed in bulk materials. The first is the sublinear dependence of ΔT_E on B due to the ${\mu B{l}_\mathrm{R}^{0}}/{W}$ term, which allows us to evaluate the electron–hole recombination length ${l}_\mathrm{R}^{0}\approx0.3\,\upmu\rm{m}$, which is close to the more accurate value derived numerically (Fig. 1l). In contrast, in the bulk limit of $W\gg \mu B{l}_\mathrm{R}^{0}$, the common linear B dependence of ΔT_E is recovered, so that we are unable to determine ${l}_{R}^{0}$ from such measurements.

Second, equation (7) predicts a non-monotonic dependence of ΔT_E on W, which describes well the behaviour in Fig. 1l (see Extended Data Fig. 1 for more details). The largest ΔT_E should be attainable for $W\approx\sqrt[3]{{W}_{\;0}^{\;2}{l}_{\,\mathrm{R}}^{0}}\mu B$ for μB < 1. From our observation of the largest transverse temperature difference in the W = 10 µm sample, we derive W₀ ≈ 24 μm. This new mesoscopic length scale W₀ arises due to the competition between the transverse heat conductivity across the sample width and the heat conductivity to the substrate and is absent in the bulk case. This length scale can serve as an important parameter for further optimization of Ettingshausen cooling in microscopic devices.

Third, we derive that the largest cooling is attained at $\hat{I}={I}_{0}/2$ and $\hat{B}=\frac{1}{\mu }\sqrt[3]{\frac{2W}{{l}_\mathrm{R}^{0}}}$ (Methods) where the negative excess temperature reaches

$$\updelta {T}_\mathrm{cold}^{\,\max}\approx-\frac{{{\epsilon }}_\mathrm{p}^{2}}{{e}^{2}{\rho }_{0}d\kappa }\frac{{W}_{0}^{\;2}{W}^{\;2}}{{\left({W}^{\,2}+{W}_{0}^{\,2}\right)}^{2}\,}.$$

(8)

For W = 20 μm, this results in $\hat{B}\approx2.2\,{\rm{T}}$ and ${\updelta T}_{\mathrm{cold}}^{\,\max }\approx-0.2\,{\rm{mK}}$, in good agreement with Fig. 2d.

Equation (8) shows that lower cooling temperatures can be attained by reducing the sample sheet resistivity ρ₀. In our WTe₂ flake, ρ₀ ≈ 0.54 Ω, corresponding to an effective bulk resistivity ρ₀d ≈ 1.5 × 10⁻⁵ Ω cm (d = 269 nm), which is almost two orders of magnitude higher than the low-temperature bulk resistivity ρ ≈ 2.3 × 10⁻⁷ Ω cm in high-quality crystals³¹. Since the increase in ρ₀ is attributed to surface oxidation⁵⁴, one can expect to attain substantially stronger cooling in devices fabricated in an inert environment and encapsulated in hBN.

Finally, from the combination of the derived parameters (Methods), we extracted the Ettingshausen conversion coefficient ϵ_p ≈ 0.06 meV, which is about one sixth of the thermal energy of the quasiparticles (k_BT₀ = 0.37 meV) and, thus, in good agreement with the description of the Ettingshausen effect in terms of particle–hole generation and recombination.

The developed nanoscale imaging of magneto-electro-thermal cooling at cryogenic temperatures in microscopic devices opens the door for studying and engineering thermal landscapes and energy harvesting in new electronic materials and devices. The derived microscopic model allows one to further enhance the cooling efficiency through the optimization of the electrical and thermal conductivity characteristics of the materials and of the device geometries. This study suggests the possibility of integrating transition metal dichalcogenide atomic layer semimetals in multilayer vdW heterostructures to provide for in-device electro-thermal cooling, temperature gradient engineering and studying thermoelectric effects in low-dimensional strongly correlated states of matter.

Methods

WTe₂ device fabrication

High-quality WTe₂ single crystals were grown using a flux growth technique⁵¹ as described in ref. ³¹. Bulk samples produced by this method showed a residual resistance ratio of 3,250, a magnetoresistance ratio of up to 62,000 at 9 T and 2 K, and a mean free path l_mr ≈ 20 µm (ref. ³¹). The crystals were then used to mechanically exfoliate WTe₂ flakes onto oxidized silicon wafers (290 nm of SiO₂). Suitable flakes, identified by optical and atomic force microscopy, were then processed by electron-beam lithography and inductively coupled plasma etching into the various geometries. The latter was done with a flow of 20 sccm of SF₆ and 10 sccm of O₂ at a radio-frequency power of 25 W, which provides an etching rate of WTe₂ of about 4.7 nm min⁻¹. Electrical contacts were fabricated by an additional electron-beam lithography step, Ar ion milling to remove the native oxide layer of WTe₂, followed by electron-beam deposition of 3 nm of Ti and Au to a thickness that exceeded the WTe₂ flake thickness. Transport measurements of the flakes show carrier mobilities of about 10,000 to 30,000 cm² V⁻¹ s⁻¹ at 4 K, corresponding to a mean free path of l_mr ≈ 0.7 to 2 µm, more than an order of magnitude lower than the bulk values due to surface oxidation and scattering, as reported previously^31,54.

SOT fabrication and thermal imaging

Nanoscale SOTs have been used as high-precision local thermometers to study dissipation in mesoscopic systems^50,55,56,57. This is achieved through the strong dependence of the SOT critical current ${I}_{\mathrm{c}}(T\;)$ on the SOT temperature. In practice, the SOT is connected in parallel with a small shunt resistor and biased above the critical current, ${I}_{\mathrm{bias}} > {I}_\mathrm{c}$. As a result, the current through the SOT ${I}_{\mathrm{SOT}}(T\;)$ has a temperature dependence that approximately follows ${I}_{\mathrm{c}}(T\;)$, with the best sensitivity in the temperature range ${T}_\mathrm{c}/2 < T < {T}_\mathrm{c}$. The thermal coupling between the SOT and the sample was achieved with a low-pressure He exchange gas. A cryogenic SQUID series array amplifier⁵⁸ was used for the I_SOT readout.

SOTs with a diameter around 110 nm were fabricated as described in refs. ^48,59. In this work, MoRe (T_c ≈ 7.2 K) was used as the superconducting material for the SOT to provide thermal sensitivity throughout the magnetic field range up to 5 T (ref. ⁴⁹) with a thermal sensitivity at zero field of 2.6 µK Hz^−1/2. Calibrating the temperature sensitivity of the SOT at zero field was carried out using a heater installed in the microscope. The relative magnetic field dependence of the sensitivity was derived by imaging the temperature of an Au thin-film heater, which was patterned next to the WTe₂ flake, versus B. The MoRe SOT was intentionally chosen to have a weak sensitivity to a magnetic field that decreased rapidly with the magnetic field⁴⁹. All data presented were acquired when the magnetic signal due to the Oersted field of the current flowing in the sample was negligible compared with the thermal signal, except for Fig. 1g, where a small signal at zero field can be resolved in the constrictions.

The SOT height was controlled by attaching the tip to a quartz tuning fork⁵⁰, which allowed scanning at a height of 80 nm above the sample surface. Thermal imaging was done at a base temperature of 4.3 K and in an environment of 40 mbar of He exchange gas to provide the thermal link between the tip and the sample⁵⁰. All images in the main text were acquired with image resolution of 344 × 269 pixels, a pixel size of 90 nm and an acquisition time of 40 ms per pixel.

For the scans in Fig. 1, an a.c. bipolar sine wave with an rms current of I = 50 μA and an excitation frequency of f = 85.37 Hz was applied, and the resulting thermal response of the SOT was measured at the first and second harmonics of f using a lock-in amplifier. Note that a current $I\left(t\right)={I}_{0}\cos (\omega t)$ creates Joule heating ${\dot{Q}}_\mathrm{J}(t)=R{I}^{2}(t)=\frac{1}{2}R{I}_{0}^{2}+\frac{1}{2}R{I}_{0}^{2}\cos (2\omega t)$, which has a d.c. component and a superimposed a.c. component at twice the excitation frequency. The latter a.c. component was measured by the second harmonic signal of the SOT.

To capture the total current-induced local temperature change in the sample δT relative to the base temperature T₀, we applied a unipolar square-wave excitation and measured the difference between the current-on and the current-off states, as presented in Fig. 2a. Negative δT means absolute current-induced cooling. That is, in the current-on state, the local temperature is lower than in the current-off state.

Analytical derivation of the Ettingshausen effect

Here we describe the simplified heat flux model. The results are in good agreement with the full numerical simulations and provide deeper insights into the role of the different parameters. We assume an approximately linear temperature gradient across the width $-{W}/{2}\le y\le {W}/{2}$ of the sample, $T\left(\;y\right)={T}_{0}-\left|\updelta {T}_{\mathrm{cold}}\right|+(0.5+y/W\;)\,\Delta {T}_\mathrm{E}$, and calculate the lateral and out-of-plane heat fluxes. The lateral heat flux through the flake from the hot to the cold side of the device is ${q}_{0}=d\kappa \Delta {T}_\mathrm{E}/W$. We compare the heat fluxes into and out of the substrate by separately considering the two regions of the sample $-{W}/{2}\le y\le 0$ and $0 < y\le {W}/{2}$. By integrating over each region, we attain the heat flux from the hotter part of the sample into the substrate:

$${q}_\mathrm{h}=\tfrac{{\kappa }^{{\prime} }}{{d}_\mathrm{s}}\int_{0}^{W/2}(T\left(\,y\right)-{T}_{0})\,\mathrm{d}y=W\kappa^{\prime} (3\Delta {T}_\mathrm{E}-4|\updelta {T}_{\mathrm{cold}}|)/8{d}_\mathrm{s}.$$

Similarly, the heat flux from the substrate into the colder side:

$${q}_\mathrm{c}=\frac{{\kappa }^{{\prime} }}{{d}_\mathrm{s}}\int_{-W/2}^{0}({T}_{0}-T(\,y))\,\mathrm{d}y=W\kappa^{\prime} (4\left|{\updelta T}_{\mathrm{cold}}\right|-\Delta {T}_\mathrm{E})/8{d}_\mathrm{s}.$$

This leads to ${q}_\mathrm{h}+{q}_\mathrm{c}=W{\kappa }^{{\prime} }\Delta {T}_\mathrm{E}/4{d}_\mathrm{s}$ and ${q}_\mathrm{h}-{q}_\mathrm{c}=W\kappa^{\prime} (\Delta {T}_\mathrm{E}-2|{\updelta T}_{\mathrm{cold}}|)/2{d}_\mathrm{s}$. The total heat flow generated by the Ettingshausen heating is, thus, described by

$$2\int_{-W/2}^{0}{\dot{Q}}_\mathrm{E}\,{\rm{d}}y\approx2{q}_{0}+{q}_\mathrm{h}+{q}_\mathrm{c}=\left(\frac{2d\kappa }{W}+\frac{W\kappa^{\prime} }{4{d}_\mathrm{s}}\right)\Delta {T}_\mathrm{E}.$$

(9)

The heat flow due to Joule heating in the same area is given by:

$$2\int_{-W/2}^{0}{\dot{Q}}_\mathrm{J}\,{\rm{d}}y={q}_\mathrm{h}-{q}_\mathrm{c}=\frac{W\kappa^{\prime} }{2{d}_\mathrm{s}}\left(\Delta {T}_\mathrm{E}-2|\updelta {T}_\mathrm{cold}|\right).$$

(10)

Introducing the length scale ${W}_{0}=\sqrt{8d{d}_\mathrm{s}{\kappa}/{{\kappa}^{{\prime}}}}$ and solving for $|\updelta {T}_{\mathrm{cold}}|$ and the temperature difference ΔT_E, thus results in

$$\Delta{T}_\mathrm{E}=\frac{{{\epsilon}}_\mathrm{p}I}{ed\kappa}\frac{2\mu B}{\left(1+\mu B{l}_\mathrm{R}^{0}/W\,\right)\left(1+{W}^{\;2}/{W}_{0}^{2}\right)},$$

(11)

$$|\updelta {T}_\mathrm{cold}|=\frac{\frac{{\rho }_{0}{I}^{2}}{4}\left(1+{\mu }^{2}{B}^{2}\right)-I\frac{{{\epsilon }}_\mathrm{p}}{e}\frac{\mu B}{1+{W}_{0}^{\,2}/{W}^{\,2}}}{d\kappa \frac{{W}^{\,2}}{{W}_{0}^{\,2}}\left(1+\frac{{\mu }^{2}{B}^{2}}{\sqrt{1+{\mu }^{2}{B}^{2}}}\frac{{l}_\mathrm{R}^{0}}{W}\right)}.$$

(12)

The current at which the Joule heating at the cold edge balances the Ettingshausen cooling, resulting in $\left|{\updelta T}_{\mathrm{cold}}\right|=0$, is thus given by

$${I}_{0}\approx\frac{{{\epsilon }}_\mathrm{p}}{e{\rho }_{0}}\frac{4\mu B}{(1+{\mu }^{2}{B}^{2})\left(1+\frac{{W}_{0}^{\,2}}{{W}^{\,2}}\right)}.$$

(13)

The maximal cooling is attained at $\hat{I}={I}_{0}/2$ and $\hat{B}=\frac{1}{\mu }\sqrt[3]{\frac{2W}{{l}_\mathrm{R}^{0}}}$, with the lowest temperature of

$$\updelta {T}_\mathrm{cold}^{\,\max}(\hat{B})\approx-\frac{{{\epsilon }}_\mathrm{p}^{2}}{{e}^{2}{\rho }_{0}d\kappa }\frac{{W}_{0}^{\;2}{W}^{\,2}}{{\left({W}^{\,2}+{W}_{0}^{\;2}\right)}^{2}\,}.$$

(14)

The fit to the experimental data is performed in three steps. The values of μ and the combined coefficient ${C}_{1}=\frac{{\epsilon }_\mathrm{p}}{e{\rho }_{0}}\frac{1}{(1+{W}_{0}^{2}/{W}^{2})}$ can be determined from fitting the line $\left|{\updelta T}_{\mathrm{cold}}\right|=0$ in the phase diagram in Fig. 2e. Subsequently, the non-monotonic dependence of ΔT_E as a function of W for a given current I in equation (11) can be used to yield estimates for W₀, ${l}_\mathrm{R}^{0}$ and the global coefficient ${C}_{2}=\frac{{{\epsilon}}_\mathrm{p}}{ed\kappa}$, as shown in Extended Data Fig. 1a,b. These values can then be used to evaluate ${\updelta T}_{\mathrm{cold}}^{\,\max }=-{C}_{1}{C}_{2}\frac{{W}_{\,0}^{\;2}}{\left({W}^{\;2}+{W}_{\,0}^{\;2}\right)\,}$ (Extended Data Fig. 1c). Finally, from C₁ and using the zero-field sheet resistance ρ₀ ≈ 0.54 Ω derived from the full numerical fits, we can evaluate ϵ_p ≈ 0.06 meV.

Figure 2e,f and Extended Data Fig. 1 show that the analytical derivation captures well the essence of the Ettingshausen effect and of the absolute cooling in mesoscopic devices, although it considers a simplified model compared with the numerical simulations presented in Figs. 1l and 2f. The fitted values of μ and ${l}_\mathrm{R}^{0}$ are slightly different between the analytical fits and the numerical simulations.

Numerical simulations

Finite-element 3D numerical simulations of the temperature maps due to Joule heating and the Ettingshausen effect in a nearly compensated semimetal were used to fit the experimental data. The calculations were conducted using COMSOL Multiphysics 5.4 in two consecutive steps. In the first step, the transport equations of a two-component conductor⁵³ were solved:

$$\frac{{l}_{\mathrm{R}}^{\;2}}{{\tau }_\mathrm{R}}\nabla \delta {n}_{\alpha }-{n}_{\alpha }{\mu }_{\alpha }{{{\mathbf{E}}}}-{{{{\mathbf{j}}}}}_{\alpha }\times (\;{\mu }_{\alpha }{{{\mathbf{B}}}})=-{{{{\mathbf{j}}}}}_{\alpha }$$

(15a)

$$\operatorname{div}{{\bf{j}}}_\mathrm{e(h)}=-\frac{\delta {n}_\mathrm{q}}{2{\tau }_\mathrm{R}},$$

(15b)

where the index α = e or h describes electrons or holes, j_α are the particle flux densities, ${{{\mathbf{E}}}}=-\nabla \phi$ is the electric field, ϕ is the electric potential, n_e and n_h are the equilibrium densities of electrons and holes, $\updelta {n}_{\mathrm{q}}=\updelta {n}_{\mathrm{e}}+\updelta {n}_{\mathrm{h}}$ is the total out-of-equilibrium quasiparticle density, ${\mu }_{{\mathrm{e}}\left({\mathrm{h}}\right)}$ is the electron (hole) mobility, τ_R is the characteristic recombination time and l_R is the recombination length. The recombination length and time are related by ${l}_{\mathrm{R}}=\sqrt{D{\tau }_{\mathrm{R}}}$, where D is the diffusion coefficient. To represent these equations, we used the Coefficients Form PDE module, which solves the general equation:

$${e}_{a}\frac{{\partial }^{2}{{{\mathbf{u}}}}}{\partial {t}^{2}}+{d}_{a}\frac{\partial {\mathbf{u}}}{\partial t}+\nabla \cdot (-c\nabla {{{\mathbf{u}}}}-\alpha {{{\mathbf{u}}}}+\gamma )+\beta \cdot \nabla {{{\mathbf{u}}}}+a{{{\mathbf{u}}}}=f,$$

(16)

where the field u is

$${{{\mathbf{u}}}}=\begin{pmatrix}\tilde{\phi}&\widetilde{\updelta{n}_\mathrm{q}}&e{j}_{\mathrm{e},x}&e{j}_{\mathrm{e},y}&e{j}_{\mathrm{h},x}&e{j}_{\mathrm{h},y}\end{pmatrix}.$$

(17)

Here $\widetilde{\phi }=\left(\frac{{e}^{2}}{h}\right)\frac{1}{{ld}}\phi$, $\widetilde{\updelta {n}_\mathrm{q}}=({{l}_\mathrm{R}}/{{\tau }_\mathrm{R}})\;e\updelta {n}_\mathrm{q}$ and l = 1 μm is a length scale for expressing u in units of current density. Equation (16) was solved in a 3D geometry that follows the dimensions of the experimental sample depicted in Fig. 1c, using fitted parameters μ_e = μ_h = 25,000 cm² V⁻¹ s⁻¹, n_e = n_h = 2.1 × 10¹⁸ cm⁻³ and ${l}_\mathrm{R}^{0}=0.5\,\upmu\rm{m}$.

The heat transport was solved in the second step of the simulation. For this, we employed a heat transfer in solids module to simulate heat diffusion in the system. The 3D geometry consisted of the WTe₂ sample of thickness d = 269 nm, heat conductivity of ${\kappa }_{\text{WT}{\text{e}}_{2}}=6.4\,{\rm{W}}\,{\rm{K}}^{-1}\,{\rm{m}}^{-1}$, a He exchange gas layer surrounding the sample that extends 1 μm above it (κ_He = 0.005 W K⁻¹ m⁻¹), a SiO₂ layer of thickness 300 nm (${\kappa}_{\text{Si}{\text{O}}_{2}}=0.2\,{\rm{W}}\,{\rm{K}}^{-1}\,{\rm{m}}^{-1}$), and a Si layer of thickness 5 μm (κ_Si = 0.32 W K⁻¹ m⁻¹), which was applied for practical convenience. From the solution of equation (16) in the first step, we calculated ${\dot{Q}}_\mathrm{E}={\epsilon}_\mathrm{p}\updelta{n}_\mathrm{q}/{\tau}_\mathrm{R}$, ${\dot{Q}}_\mathrm{J}=-{\mathbf{J}}\cdot \nabla \phi$, and $\dot{Q}={\dot{Q}}_\mathrm{J}+{\dot{Q}}_\mathrm{E}$ with ϵ_p = 0.16k_bT₀ = 0.06 meV, and used these as the heat sources for the heat transfer module to solve for δT_E, δT_J and δT. The bottom side of the Si layer was set as the thermal anchor to T₀ = 4.3 K.

Note that although ${l}_\mathrm{R}^{0}$ and μ affect the fitting to the experimental data substantially, the rest of the parameters provide a fit over a range of values. The simulations presented should, thus, be considered as a qualitative demonstration of the validity of the model rather than an accurate determination of the parameter values.

Ettingshausen effect in additional samples

Strip geometry

To exclude excess heating arising from the narrow constrictions in the rectangular chamber geometry, a sample with a strip geometry (Extended Data Fig. 2a) of width W = 20 µm and thickness d = 160 nm was investigated. By applying a sinusoidal a.c. current with I = 50 µA at B = 5 T, we acquired the maps of δT_J and δT_E shown in Extended Data Fig. 2d,e. The absence of the constrictions resulted in more uniform temperature distributions in the device compared with Fig. 1f,i. The slight canting of the thermal distributions in Extended Data Fig. 2d,e is probably due to the small Hall voltage resulting from incomplete compensation between the electron and hole densities and mobilities and shows an opposite tilt angle upon reversing the magnetic field direction (Supplementary Information). A quantitative analysis of the field dependence of δT_J at the centre of the device (Extended Data Fig. 2b) shows quadratic behaviour that approximately follows the B dependence of the sample resistivity, whereas the temperature difference ${\Delta T}_\mathrm{E}={\updelta T}_\mathrm{E}\left(0,-{W}/{2}\right)-\updelta {T}_\mathrm{E}\left(0,{W}/{2}\right)$ between the hot and cold edges across the centre of the strip shows an approximately linear B dependence consistent with Fig. 1k,l.

Applying a unipolar square-wave excitation with I = 8 µA at B = 5 T reveals absolute cooling at the top edge in Extended Data Fig. 2f. The phase space for absolute cooling was found by mapping δT_cold versus B and I, as shown in Extended Data Fig. 2c. The overall behaviour is like the W = 20 µm device in Fig. 2e with comparable δT_cold values. The main two quantitative differences, however, are the position of the peak of ${I}_{0}(B)$, which occurs at B ≈ 1.1 T in Extended Data Fig. 2c, and the maximal negative $\updelta {T}_{{{\mathrm{cold}}}}^{\max }$ attained at $B\gtrsim \, 5$ T. By fitting the ${I}_{0}\left(B\right)$ (dashed line in Extended Data Fig. 2c), we find μ = 9,000 cm² V⁻¹ s⁻¹. This lower value is consistent with this device being thinner^31,54.

Rectangular geometry

We present here thermal imaging of an additional two chambers of width W = 10 and 5 µm connected in series with the W = 20 µm chamber described in the main text (Fig. 1c). Extended Data Fig. 3a–c shows δT_J maps at B = 0, 1 and 5 T in the W = 10 µm chamber at I = 50 µA with corresponding δT_E maps in Extended Data Fig. 3d–f. A similar set of data is presented in Extended Data Fig. 3g–l for the W = 5 µm chamber. The qualitative behaviour is like that of the W = 20 µm chamber. However, ∆T_E shows a non-monotonic dependence on W, as described in Fig. 1l.

Additional geometries

Additional samples with more complex geometries are presented in Extended Data Fig. 4. Since an accurate calibration of the SOT thermal response was not available in this set of experiments, the data are presented in relative units.

Extended Data Fig. 4a,d shows a sample with thickness d = 110 nm, which allows the application of current through channels of different widths and along different directions. For the current path shown in Extended Data Fig. 4a, the largest δT_J was observed in Extended Data Fig. 4b in the two narrowest channels on the left and right sides. In contrast, the largest transverse ∆T_E occurs in the widest top left channel in Extended Data Fig. 4c. Additionally, strongly non-local Ettingshausen heating and cooling can be observed in the vicinity of the right-angled corners along the current path, as discussed below.

Application of the current along the central vertical channel in Extended Data Fig. 4d reveals that ∆T_E in the vertical strip sections in Extended Data Fig. 4f is smaller than the Ettingshausen heating and cooling spots appearing at the junctions with the horizontal channels. The temperature maps for the two different current paths in the sample illustrate the mesoscopic nature of the Ettingshausen effect, as discussed in the main text, along with its non-local character. The Joule heating is local in nature because ${\dot{Q}}_\mathrm{J}$ is mainly determined by the local J. In contrast, ${\dot{Q}}_\mathrm{E}$ is not determined by the local P but rather by $\nabla \cdot {{{\mathbf{P}}}}$.

These features were further corroborated by thermal imaging of the sample shown in Extended Data Fig. 4g, which has thickness d = 48 nm and was used in ref. ³¹. This sample consists of a very narrow strip of W = 0.55 µm connected to two circular discs of 1.8 µm diameter. Extended Data Fig. 4h,i shows that δT_J is largest along the narrow horizontal strip, whereas ∆T_E is vanishingly small. In narrow channels, with width comparable to l_R, the regions of electron–hole generation and recombination partially overlap and the induced Ettingshausen temperature gradient is greatly suppressed by the large transverse heat conductivity across the narrow channel. In sharp contrast, Extended Data Fig. 4i shows very pronounced Ettingshausen heating and cooling in the circular chambers, where almost no current flows, emphasizing its non-local character.

Qualitatively, the dependence of δT_E on the channel width can also be seen in the temperature maps of the sample depicted in Extended Data Fig. 4j,m, which has two connected channels of different widths and a thickness of d = 105 nm. As seen in Extended Data Fig. 4l, the temperature difference between the hot and cold edges ∆T_E is larger in the wider channel and there is a pronounced increase in Ettingshausen heating and cooling at the corners, like the results in the main text (Fig. 1h,i). As expected for the Ettingshausen effect, δT_E reverses sign upon reversing the magnetic field direction in Extended Data Fig. 4o, whereas the Joule heating shown in Extended Data Fig. 4k,n remains unaffected.