Abstract
Quantum devices characterized by non-Hermitian topology are predicted to show highly robust and potentially useful properties for precision sensing and signal amplification. However, realizing them has remained a daunting experimental task, as non-Hermiticity is often associated with gain and loss, which would require precise tailoring to produce the signatures of non-trivial topology. Here, instead of gain and loss, we use the non-reciprocity of quantum Hall edge states to directly observe non-Hermitian topology in a multi-terminal quantum Hall ring. Our transport measurements evidence a robust, non-Hermitian skin effect, characterized by currents and voltages showing an exponential profile that persists across Hall plateau transitions away from the regime of maximum non-reciprocity. Our observation of non-Hermitian topology in a quantum device introduces a scalable experimental approach to construct and investigate generic non-Hermitian systems.
Similar content being viewed by others
Main
Hermitian quantum mechanics describes isolated quantum systems. These include conventional topological phases occurring in the ground states of certain materials1, such as the well-known quantum Hall phase, whose precisely quantized electrical resistance is used today in metrology2. When coupling a quantum device to the outside world, however, the resulting gain and loss lead to an effectively non-Hermitian description3. Non-Hermitian systems can also be topologically non-trivial4 and thus have robust properties, some of which hold the promise for remarkable applications. These include exponentially precise sensors5, amplifiers6 and light funnels7.
Introducing gain and loss in a quantum device is easily achieved, for instance, by not shielding it sufficiently well from its local environment. However, customizing these two processes such as to reach a topological phase has so far remained challenging, and no quantum, condensed-matter devices showing non-Hermitian topology have been reported to date. Instead, the existing experimental observations have been achieved using ultracold atoms8 and optical systems9,10, as well as by using metamaterials governed by the laws of classical physics. The latter include electronic circuits11,12 and photonic crystals7, as well as mechanical13,14 and acoustic15,16 systems. Their operating principle is based on the fact that Kirchoff’s laws, Newton’s laws and Maxwell’s equations can be used to mimic the Schrödinger equation describing the dynamics of quantum particles.
Here we directly observe one of the characteristic signatures associated with non-Hermitian topology in the quantum regime of a condensed-matter system. Rather than relying on gain and loss, we build on the quantum transport properties of a well-known, Hermitian topological phase: the quantum Hall phase. Its unidirectional edge modes provide a link to non-Hermitian topology that can be accessed in conventional multi-terminal conductance measurements. Our work introduces non-Hermitian topology and its potential applications to the field of experimental mesoscopic physics. It opens the possibility to create devices that take advantage of this type of topology, not just by using the quantum Hall effect but also more generally by relying on the quantum transport properties of condensed-matter systems.
We start from one of the simplest examples of non-Hermitian topology—the Hatano–Nelson (HN) model17. The Hamiltonian,
describes a chain on which quantum particles hop between neighbouring sites (site index j and creation operator \({c}_{j}^{{\dagger} }\)), where the hopping to the left and to the right are real numbers with different magnitudes, namely, Jleft ≠ Jright. Here c is a column vector formed from all the annihilation operators and HHN is the Hamiltonian matrix, whose size is given by the number of sites in the chain.
This model is non-Hermitian, that is, \({{{{\mathcal{H}}}}}_{{{{\rm{HN}}}}}^{}\ne {{{{\mathcal{H}}}}}_{{{{\rm{HN}}}}}^{{\dagger} }\), due to the non-reciprocal hoppings, and it is characterized by a net bulk current flowing in the direction of the larger hopping18. Heuristically, all the states in the bulk of the system will flow in the current direction, until eventually reaching the end of the chain. This is the boundary signature associated with its non-trivial topology, the non-Hermitian skin effect: in a finite chain with open-boundary conditions (OBCs), all the eigenstates are exponentially localized at one end of the system (Methods and Extended Data Fig. 1).
Our work is based on the insight that in the limit of maximum non-reciprocity, when the hopping in one direction vanishes identically, the HN model effectively describes a one-dimensional, unidirectionally propagating mode. Thus, the Hamiltonian in equation (1), even though it is non-Hermitian, provides an accurate description of the long-time dynamics of the quantum Hall edge19,20.
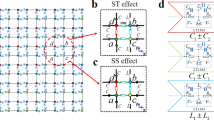
Starting from this insight, we have designed a multi-terminal quantum Hall device (Fig. 1a,b). It consists of a two-dimensional electron gas (2DEG) ring etched in an AlGaAs/GaAs semiconducting heterostructure (Supplementary Section 1), with the arms distributed along its outer perimeter. Each arm consists of an ‘inner’ ohmic contact, directly connected to the ring, and an ‘outer’ contact, which is singly connected to the inner contact via a separate section of the 2DEG (Fig. 1b). We label an arm as ‘active’ when its inner contact is connected to a voltage probe and/or a current source. The outer contacts of the active arms can be either grounded or floating. In contrast, for an ‘inactive’ arm, no current sources or voltage probes are attached to either contact. The contacts of an inactive arm can be either grounded or floating. There are a total of ten arms, but since the total number of measurements required scales quadratically with the number of active arms, not all of them are used. Two examples of possible measurement configurations are shown in Fig. 1c,d.
a, Scanning electron microscopy (SEM) image of the AlGaAs 2DEG device. b, Zoomed-in false-colour SEM image. The white lines indicate the edge quantum Hall states occurring in the presence of a perpendicular magnetic field at filling factor ν = 1, whereas the white arrows indicate the direction of propagation of electrons. The 2DEG and ohmic contacts are highlighted in red and yellow, respectively. The white dashed lines show the boundaries of the 2DEG. c, Five-site OBC configuration where the grounded inactive arm (grey) is used to disconnect the first and last site of the chain. The schematic of the effective corresponding HN chain is shown below. The active arms are labelled using currents and voltages, namely, Ij and Vj, respectively. For the inactive arms (dashed lines), both contacts are floating. d, Five-site PBC configuration, with the schematic of the effective HN chain shown below. e, Measured magnetoresistance of all the five sites of the OBC setup at T = 2.7 K for current I2 = 10 nA injected into the second site (the resistance matrix is explicitly shown in Supplementary Section 2). f, Measured magnetoresistance of the PBC setup for current I2 = 10 nA injected into the second site. g, Real part of the five-site G matrix measured at B = 11.5 T (ν = 1) for the OBC configuration under the same conditions as those in e. h, Real part of the five-site G matrix measured under the same experimental conditions for the PBC configuration under the same conditions as those in f.
To highlight the connection between this device and non-Hermitian topology, we begin by considering the case of a single current source, which injects a current Ij into the jth active arm of the ring. In the linear regime, the current Ij is related to the voltages Vi of the active arms as Ij = ∑iGjiVi, where G is the conductance matrix. In the presence of time-reversal symmetry, Gij = Gji, such that the conductance matrix is Hermitian. A magnetic field breaks this condition and induces non-Hermitian terms in G. Considering, for instance, the device in the quantum Hall regime at filling factor ν and in the presence of perfect contacts, the only non-zero elements of G will be on its diagonal, as well as between adjacent contacts in the direction of propagation of the edge modes. For the jth active arm (with j > 1),
where α = 1 if the outer contact of the arm is floating (Fig. 1c) and α = 2 if the outer contact is grounded (Fig. 1d) and all the inactive arms between j − 1 and j are floating. For the contact configurations shown in Fig. 1c,d, the G matrix is, therefore, related to the HN Hamiltonian matrix with Jleft = 0 and Jright = − 1:
where \({\mathbb{1}}\) is the identity matrix.
The above equation lends itself to two different physical interpretations. The first is that the quantum Hall ring is a metamaterial. It is a way of generating a matrix G that is equivalent to the Hamiltonian matrix HHN of a non-Hermitian quantum system, which would otherwise be out of experimental reach. In this interpretation, the inner contact of each active arm of the quantum Hall ring plays the role of a site in the HN model, and the conductance matrix takes the role of the Hamiltonian. In the second interpretation, equation (3) means that due to the chiral nature of their edge modes, Chern insulators should show quantum transport properties whose presence and robustness are a consequence of non-Hermitian topology21. In the following, we shall explore the experimental consequences of both approaches.
Seen as a metamaterial, the quantum Hall ring allows us to test two different configurations, equivalent to different realizations of the HN model. The first corresponds to OBC (Fig. 1c), where the chain is cut between the last and first site. This is achieved by grounding the inner contact of an intermediate inactive arm (between j = N and j = 1), thereby setting I1 = ανe2/hV1. For periodic-boundary conditions (PBCs; Fig. 1d), on the other hand, all the inactive arms between j = N and j = 1 are floating, and the last site N of the chain is connected to the first one: I1 + νe2/h(VN − αV1) = 0. In the OBC configuration, the outer active contacts can be either grounded or floating without affecting the topological properties of the chain, whereas in the PBC configuration, Kirchhoff’s laws require them to be grounded.
Experimentally, measuring the elements of G will be achieved by first determining the elements of its inverse, namely, the resistance matrix R = G−1. Injecting the current in each of the active arms, one by one, and measuring the voltages of all the active arms using lock-in amplifiers yields each column of R (Supplementary Section 2). The measurements of the second column of R for any magnetic field and for the OBC and PBC configurations are shown in Fig. 1e,f, respectively.
Permuting the position of the current source allows us to determine the full R matrices. The corresponding conductance matrices G are shown in Fig. 1g,h, respectively. Owing to the robustness of the quantum Hall edge modes, the resulting, experimentally measured conductance matrix at ν = 1 is remarkably close to that of a perfect, five-site HN chain (equation (3)) with Jleft = 0, Jright = −1 and α = 2. We find that deviations in the individual matrix elements from the perfect values are of the order of a few per cent or less.
Beyond the two configurations discussed above, the quantum Hall ring also allows us to continuously tune the effective HN chain from OBC to PBC. As shown in Fig. 2a, for a six-site chain, this is achieved by connecting the inner contact of one of the inactive arms between j = N and j = 1 to the ground via a variable resistance RG, whereas its outer contact is floating. Changing the value of RG serves to continuously tune the system between the grounded and floating configurations shown in Fig. 1c,d and hence to tune it from OBC to PBC (Fig. 2b,c).
a, Schematic of the link between contacts 1 and 6, including a variable resistance RG at the end of the chain for continuous tuning between OBCs and PBCs. b, Real part of the conductance matrix for the six-site configuration at B = 11.5 T (ν = 1). Changing the variable resistance RG affects the top-right element of the matrix (in white). This dependency is shown in c. c, Coupling term G16 versus resistance RG in the logarithmic scale. The data points corresponding to those shown in the next panels are highlighted using squares. d, Eigenvalues of the experimental G matrix (labelled λ) for the four selected points in units of e2/h. The average diagonal element of the matrix is subtracted to centre the plot around zero for better readability. We note that the eigenvalues do not completely collapse on a single point on the real axis. This is attributed to the finite resistance of the measurement line of the grounded contact (Supplementary Section 3). e, SPDs in the logarithmic scale obtained by diagonalizing the measured G matrix for the highlighted data points, plotted as a function of the lead index. The evolution from a constant to an exponentially decaying profile indicates the appearance of a non-Hermitian skin effect on gradually changing from PBC to OBC. The markers indicate the experimental data points, and the lines are the best exponential fit to the data.
As expected, numerically diagonalizing the G matrix yields all the signatures associated with the non-Hermitian topology in the HN model22. With PBC, its discrete eigenvalues are positioned along a circle in the complex plane, and gradually tuning towards OBC causes the eigenvalues to move to the inside of this circle (Fig. 2d). This is consistent with the theoretical prediction that all OBC eigenvalues are contained within the contour formed by the PBC spectrum (Methods). At the same time, the probability density summed over all the eigenvectors of the G matrix (sum of probability densities (SPDs), defined in Methods) shows the non-Hermitian skin effect. With PBC, this density is uniformly spread across the sites of the chain (meaning the arms of the ring), whereas moving towards OBC causes the probability density to become exponentially localized on the last site (Fig. 2e, Methods and Supplementary Section 3), demonstrating the topologically non-trivial character of our device.
In the HN model, the presence and robustness of the non-Hermitian skin effect is predicted by a non-zero bulk invariant, similar to how the Chern number predicts the appearance of chiral edge modes. For an infinite, translationally invariant chain, the non-Hermitian invariant is the winding number of the bulk bands as a function of momentum (Methods). In our system, we have a finite number of sites, meaning that the bands are replaced by discrete eigenvalues. To capture the non-Hermitian topology of the conductance matrix and therefore the robustness of the skin effect, we determine the topological invariants based on the methods recently developed for finite systems23,24. We use two distinct methods to determine the invariant and to consequently confirm that the non-Hermitian skin effect has a topological origin. The two methods lead to invariants labelled as wPD and wL. The wPD invariant is based on the polar decomposition (PD) of the HN model, and was recently shown to correctly capture the topology of a finite-sized chain with OBC23. It can take any real value, but approaches a quantized integer deep in the topological phase. The wL invariant, on the other hand, is an integer by construction. It is based on the so-called spectral localizer, a mathematical object that has so far been used for the description of both Hermitian24 and non-Hermitian systems25,26, and which we now apply to the HN model, again with OBC. Both invariants are directly computed from the measured OBC conductance matrices, by using the formulas described in Methods.
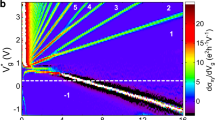
As shown in Fig. 3, the invariants reflect the non-trivial topology of the G matrix at large magnetic fields. Depending on the direction of the magnetic field and therefore of the chiral edge modes, both wPD (Fig. 3a) and wL (Fig. 3b) remain quantized to either +1 or −1, respectively. Consistent with this, we find that the non-Hermitian skin effect is present either at the left or the right end of the chain (Supplementary Section 4), with all the eigenvectors positioned there. Remarkably, the deviations of wPD from the expected quantized value for a five-site chain remain on the order of 10−3 to 10−4 for a wide range of magnetic fields, including those across plateau transitions (Fig. 3c). Consistent with this, the non-Hermitian skin effect is even present for magnetic fields at which the Hall conductance is not quantized (Supplementary Section 4). Thus, we find that the non-Hermitian invariant is more robust than the Chern number. This is the case, for instance, when the magnetic field sets the position of the Fermi energy on a Landau level, or when the formation of Landau levels is prevented by disorder—at very low mobility and high temperature or at low magnetic fields—and therefore when the Chern number is not defined (Supplementary Section 5). The best quantization of wPD improves to an accuracy of 10−5 for an eight-site chain and for Fermi energy set between two Landau levels. It should be improved further for a larger number of sites until it will be limited by the coupling between the last (j = N) and the first (j = 1) sites, the coupling to previous sites (backscattering) or the noise level of the measurements (Supplementary Sections 3 and 6). Finally, we note that the field asymmetry observed in Fig. 3c is a result of the onsite disorder in the HN chain (Supplementary Section 7).
a,b, PD of the real-space topological invariant wPD (a) and localizer index wL (b) for a five-site OBC setup versus a perpendicular magnetic field. c, Deviation of the PD of the real-space invariant from the expected values (−1 for positive fields and +1 for negative fields), plotted on a logarithmic scale versus the magnetic field. The inset shows the invariant deviation measured at various temperatures in a quantum Hall effect plateau at B = 3.5 T, averaged over 100 mT. The blue colour denotes the temperatures for which a quantum Hall plateau is measured, whereas the red colour denotes the temperatures for which only dips (and no plateaus) are measured (Supplementary Fig. 9). The vertical dashed line is a guide for the eyes.
We now discuss the transition between the classical diffusive regime and the quantum Hall regime with maximum non-reciprocity. In the classical regime, as well as between the quantum Hall plateaus, equations (2) and (3) are not valid anymore and finite long-range couplings (between distant sites) appear in the conductance matrix, similar to the conductance matrix at zero magnetic field. The emergence of finite off-diagonal elements in the upper triangle of the conductance matrix leads to a less robust quantization of wPD and a broader skin effect (Supplementary Section 3). We tune the amplitude of the off-diagonal elements by varying the magnetic field on one hand and the mobility on the other hand by changing the temperature. At small magnetic fields, namely, ∣B∣ ≲ 0.4 T, both invariants and skin effect lose their robustness (Supplementary Section 4). wPD becomes poorly quantized (Fig. 3c), whereas wL, which is an integer by definition, becomes equal to 0 or begins to rapidly oscillate between the values −1, 0 and +1. This behaviour is a typical signature of topological phase transitions occurring in finite-sized systems (here a five-site chain).
A similar loss of robustness is observed as a function of increasing temperature. To tune the onset of the quantum regime, the conductance matrix was measured at different temperatures between 470 mK and 80 K, thus changing the mobility of the device over a broad range. The topological invariants are calculated at all fields and temperatures (Supplementary Section 5). To highlight the importance of quantum effects, we show (Fig. 3c, inset) the temperature dependence of the invariant quantization at a fixed magnetic field. When the temperature is lowered and the system enters a quantum Hall plateau regime, the invariant quantization shows a sharp improvement, by a factor between 3 and 4. We have confirmed that the best quantization is systematically obtained for magnetic fields and temperatures that set the system well on a quantum Hall effect plateau.
Surprisingly, for small fields, the field dependence of the invariant quantization is roughly temperature independent and therefore mobility independent. It scales quadratically with the field, even far into the classical regime (Supplementary Section 5). In contrast, two measurements done with two different electronic densities indicate that the electron density strongly influences the field dependence of the invariant quantization: the lower the density, the sharper the decay (Supplementary Section 5). We note that unexpected features are brought to light by the results at the highest temperatures (T = 50 and 80 K), where the evolution of the topological invariants shows jumps that are discussed in more detail in Supplementary Sections 5 and 7.
In analogy to the methods commonly used in metamaterials such as topoelectric circuits, we have so far measured the R = G−1 matrix element by element using a single current source, and then examined the topological features by numerically diagonalizing the G matrix. In contrast, the conventional quantum Hall effect, meaning the robust quantization of the Hall conductance, is a directly observable physical phenomenon, independent of any effective model.
Turning to the second interpretation of equation (3), we now show that—similar to the quantized Hall conductance of the quantum Hall effect—the topological, non-Hermitian skin effect is a directly observable transport property of our device, which does not require the determination of the G matrix or its numerical diagonalization. To achieve this, we make use of the fact that the skin effect implies that all the eigenvectors of the conductance matrix are exponentially localized at one boundary of the system. One general numerical method to determine an eigenvector is the so-called iterative power method. By iteratively applying a matrix A to a random non-zero vector x, one converges towards the largest eigenvalue λ of A:
where v is the eigenvector of A associated with λ. This can be experimentally realized in our device by simultaneously applying different random currents to all the active contacts using multiple current sources (and therefore having a random current vector I0 = (I1,…, IN); Fig. 4a), followed by measuring the resulting voltages Vj of each site j, and then iteratively reapplying currents to each contact such that the new current vector is proportional to the previous voltage vector In+1 ∝ Vn. This is effectively applying Gn to the current vector I0 (Fig. 4b). Repeating this iteration should drive voltages to converge towards one of the eigenvectors of G, all of which show the non-Hermitian skin effect.
a, Elements of the initial, randomly generated current vector (Methods) displayed in polar coordinates for a six-site setup. The amplitude is normalized such that the different coordinates are in units of the largest injected current (150 nA). The measurement is performed at B = 5.5 T (ν = 2) b, Flow chart of the iterative procedure. c, Final current configuration in the system after 40 iterations. d, Evolution of the phase of each vector element versus the iteration number. The system converges to a final current configuration with a unique phase as a function of the iteration number (Methods). e, Evolution of the amplitude of each element versus the iteration number, in units of the largest injected current (150 nA). The final current configuration is reached after 15 to 20 iterations, when the amplitudes no longer change as a function of the iteration number. This final current configuration shows an exponential decay as a function of the lead index, from 6 to 1 (from dark to light blue), which is a direct manifestation of the non-Hermitian skin effect in experiment (Methods).
We applied this scheme to our quantum Hall device with six active contacts, labelled 1 to 6. After 15 to 20 such iterations, we observe that both current and voltage vectors become independent of the iteration step (Fig. 4c). After having converged, both vectors show an exponentially decaying profile over the contacts from 6 to 1 (Fig. 4d,e). This constitutes a direct measurement of the non-Hermitian skin effect: the current vector converges to one of the eigenvectors of the conductance matrix (Methods and Extended Data Fig. 2), all of which are exponentially localized to one end of the HN chain (contact 6 in our case). The exponential nature of the current and voltage profiles is a robust transport signature of our quantum device. It does not change for a wide range of magnetic fields, it is independent of the initially chosen currents and it is only present in the OBC configuration (Methods and Extended Data Fig. 3). The robustness of this multiple-source transport signature is a direct consequence of the non-Hermitian topology in our quantum Hall ring.
Methods
HN model
The HN model is the simplest example of a non-Hermitian system with non-reciprocal hoppings. Defined on a one-dimensional lattice with no symmetry requirements, this model can be described by a single-orbital tight-binding Hamiltonian17:
where Jleft and Jright ∈ R are unequal hopping amplitudes. For a finite-sized chain in real space, the Hamiltonian matrix takes the form
If the chain is infinitely long, Fourier transforming yields the following one-band Bloch Hamiltonian:
Its eigenvalues form an ellipse in the complex plane and wind around the origin. The corresponding non-Hermitian winding number w takes the general form27
where EB is the so-called base point, that is, the point in the complex plane at which the winding number is evaluated. This invariant characterizes the non-Hermitian topology of the system, manifesting itself in the non-Hermitian skin effect.
Calculating equation (8) for H(k) at EB = 0 gives
The eigenvalues and eigenvectors of \({{{{\mathcal{H}}}}}_{{{{\rm{HN}}}}}^{}\) are sensitive to the boundary conditions imposed on the system. Under OBCs, the eigenvalues are real (Extended Data Fig. 1a). Defining the SPDs at the jth lattice site as \({\sum }_{i}{\left\vert \left\langle {r}_{j}| {{{\varPsi }}}_{i}\right\rangle \right\vert }^{2}\), where |Ψi〉 are the right eigenvectors of \({{{{\mathcal{H}}}}}_{{{{\rm{HN}}}}}^{}\) and |rj〉 denote the lattice site positions, we observe that an extensive number of eigenstates are localized at the ends of the system (Extended Data Fig. 1b shows the OBC configuration), a phenomenon unique to non-Hermitian systems and commonly referred to as the non-Hermitian skin effect28. Moreover, this localization occurs at the right (left) end of the system for |Jright|/|Jleft| > 1 (|Jright|/|Jleft| < 1) and is related to the non-trivial winding of the energy bands22. However, with PBCs, the spectrum consists of discrete points positioned on an ellipse (Extended Data Fig. 1a), thus reproducing the behaviour of the Bloch Hamiltonian characterizing the infinite system (equation (7)). The system’s translational invariance leads to a constant SPD (equal to 1) on all the sites (Extended Data Fig. 1b).
When approaching the limit of maximum non-reciprocity, that is, Jleft = 0 and Jright = 1, the PBC spectrum evolves towards a circle in the complex plane, whereas the OBC spectrum moves towards the origin, that is, E = 0. A gradual transition between PBC and OBC then involves a shrinking of the initially circular spectrum: eigenvalues progressively move inside of the contour defined by the PBC spectrum, as evident from the experimentally determined G matrix (Fig. 2). Further, slight deviations in the matrix elements away from the perfect limit of equation (6), which in experiment are of the order of a few per cent or less, lead to slight changes in the positions of individual eigenvalues.
Experimental determination of the SPD
In our experimental setup, determining the SPD involves the components of the G matrix eigenvectors. Labelling \({V}_{i}^{\,j}\) as the ith component (related to the site i of the chain) of the jth normalized eigenvector Vj of the experimentally determined G matrix, the SPD reads
where SPD(i) is the SPD at site i.
Real-space topological invariants
A recent work has proposed a real-space formula to calculate the topological invariant of finite-sized HN chains23. This invariant, which we label wPD, uses the PD of the Hamiltonian matrix at base point EB:
where Q is unitary and P is a positive-definite matrix. wPD takes the form
where X = diag(1, 2,…, L) encodes the positions of the sites of the HN chain and \({{{\mathcal{T}}}}\) is the trace per unit volume evaluated over a middle interval of the chain, namely, [l + 1, L − l].
Since the conductance matrix G shown in the main text describes an effective one-dimensional HN model, we replace HHN in equation (11) by G to determine the associated invariant. For the six-site setup (L = 6), we have chosen l = 2, and EB is the arithmetic mean of the diagonal entries of the conductance matrix G. In general, for a long enough chain, the choice of l is not expected to qualitatively change the value of wPD, provided that the trace of equation (12) is performed over sites sufficiently far from the boundaries of the chain23.
The second invariant, wL, is based on the so-called spectral localizer, a mathematical object recently used to derive topological invariants for finite-sized Hermitian systems24,29,30. We adapt this invariant to the HN model by using the fact that non-Hermitian topology is related to Hermitian topology by doubling the Hamiltonian22. In our case, the HN Hamiltonian matrix is related to the well-known Su–Schrieffer–Heeger31 model as
It has been shown that the topological invariant of HSSH is equal to that of HHN evaluated at base point EB (ref. 22). Thus, we use equation (13) together with the localizer index of the Su–Schrieffer–Heeger chain24, resulting in
Here sig denotes the matrix signature, that is, the number of positive eigenvalues minus the number of negative eigenvalues, and X labels the sites in the chain, now with the condition that the origin is positioned close to the middle of the system: \(X={{{\rm{diag}}}}(0,1,2,\ldots ,L-2,L-1)-\lfloor L/2\rfloor {\mathbb{1}}\), where ⌊x⌋ is the integer part of x. As before, we replace the HN Hamiltonian matrix with the measured conductance matrix G and set EB to be the mean of its diagonal elements.
Details of the iterative measurement
The iteration process at the jth iteration consists of injecting a sine-wave current vector I(j, n) where n stands for an effective time of the sine-wave functions. Each component i of the current vector is the addition of a constant C independent of i (see below) and n and a sine function characterized by its phase ϕi(j), and of its amplitude Ai(j) > 0. The component i of the current vector corresponds to the current injected into the lead i. Ai(j) and ϕi(j) are randomly generated for j = 0. To generate the sine functions, we discretize the signal in N regularly spaced points. Each point indexed by n with n ∈ {0,…, N − 1} coincides with a 2πn/N phase in the sine functions.
For the six-site configuration we used, the current vector reads
The amplitudes are normalized in our experiment such that \(\mathop{\max }\nolimits_{i}({A}_{i})+C\) = 150 nA, and we choose C = 75 nA such that all the components of the current vector are positive for any value of n. We used the lock-in amplifier’s voltage source and a polarization resistance of 1 MΩ to generate a.c. current sources, whose amplitudes correspond to the related component of the current vector. We used a total number of N = 30 points, which allow for a reliable determination of the amplitudes and phases of the current vector’s sine-wave components.
For a six-site setup and for the jth iteration, a current vector as defined in equation (15) is applied 30 times with n = 0,…, 29, and the corresponding voltage vector is measured for each n. This allows us to determine the relative amplitude and phase of the different components of the voltage vector for the jth iteration. The amplitude and phase of the current vector j + 1 is given by the renormalization of the voltage vector j such that \(\mathop{\max }\nolimits_{i}({A}_{i})=C\) = 75 nA.
The evolution of the measured voltage vector components versus iteration index is shown as an animation for the six-site setup in the data associated to this work32, with the snapshots shown in Extended Data Fig. 2.
We have measured eight different iteration processes in the OBC, all of them ending in a final current configuration corresponding to the eigenvector associated with the same eigenvalue of the G matrix, regardless of the starting configuration. This eigenvector has all the components in phase. Its related eigenvalue is real, meaning that the current and voltage of each contact are in phase. The final current and voltage configuration, thus, presents a skin effect (Extended Data Fig. 3a). We have also performed six iteration processes in the PBC configuration (Extended Data Fig. 3c) to confirm that the skin effect is not present in this case.
To quantify how fast the iteration process converges on its final current configuration, we introduce the quantity Δ as a function of iteration step j, which is defined as
where I(j, n) is the current vector defined above, and where j → ∞ corresponds to the final iteration step. Extended Data Fig. 3b,d represents the value of Δ(j)/Δ(0) for OBC and PBC, respectively. We observe a convergence to the final configuration in about ten iterations for OBC, which is substantially reduced for the PBC, where only about five iterations are needed to reach the final configuration.
To understand the convergence of the system gradually to an eigenvector of the G matrix, one needs to consider the eigenvalues λi and eigenvectors ui of the G matrix. Such a convergence can be simply understood considering the projection of the initial current vector I(0) onto the eigenvector umin associated with the eigenvalue λmin with \(| {\lambda }_{\min }| =\mathop{\min }\nolimits_{i}(| {\lambda }_{i}| )\) in absolute value. We then have
Since all the eigenvectors of the G matrix show a skin effect, the system always converges to a current and voltage configuration that shows this skin effect. This convergence is a direct signature of the topologically non-trivial non-Hermiticity of the system.
Data availability
The data associated with this work is available via Zenodo at https://doi.org/10.5281/zenodo.6985564 (ref. 32).
Code availability
The code used in this work is available via Zenodo at https://doi.org/10.5281/zenodo.6985564 (ref. 32).
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Klitzing, K. V., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494 (1980).
Ashida, Y., Gong, Z. & Ueda, M. Non-Hermitian physics. Adv. Phys. 69, 249–435 (2020).
Bergholtz, E. J., Budich, J. C. & Kunst, F. K. Exceptional topology of non-Hermitian systems. Rev. Mod. Phys. 93, 015005 (2021).
Budich, J. C. & Bergholtz, E. J. Non-Hermitian topological sensors. Phys. Rev. Lett. 125, 180403 (2020).
Wang, Q., Zhu, C., Wang, Y., Zhang, B. & Chong, Y. Amplification of quantum signals by the non-Hermitian skin effect. Phys. Rev. B 106, 024301 (2022).
Weidemann, S. et al. Topological funneling of light. Science 368, 311–314 (2020).
Liang, Q. et al. Observation of non-Hermitian skin effect and topology in ultracold atoms. Phys. Rev. Lett. 129, 070401 (2022).
Xiao, L. et al. Non-Hermitian bulk-boundary correspondence in quantum dynamics. Nat. Phys. 16, 761–766 (2020).
Wang, H. et al. Topological physics of non-Hermitian optics and photonics: a review. J. Opt. 23, 123001 (2021).
Helbig, T. et al. Generalized bulk–boundary correspondence in non-Hermitian topolectrical circuits. Nat. Phys. 16, 747–750 (2020).
Liu, S. et al. Non-Hermitian skin effect in a non-Hermitian electrical circuit. Research 2021, 5608038 (2021).
Brandenbourger, M., Locsin, X., Lerner, E. & Coulais, C. Non-reciprocal robotic metamaterials. Nat. Commun. 10, 4608 (2019).
Ghatak, A., Brandenbourger, M., Van Wezel, J. & Coulais, C. Observation of non-Hermitian topology and its bulk-edge correspondence in an active mechanical metamaterial. Proc. Natl Acad. Sci. USA 117, 29561–29568 (2020).
Zhang, X., Tian, Y., Jiang, J. H., Lu, M. H. & Chen, Y. F. Observation of higher-order non-Hermitian skin effect. Nat. Commun. 12, 5377 (2021).
Zhang, L. et al. Acoustic non-Hermitian skin effect from twisted winding topology. Nat. Commun. 12, 6297 (2021).
Hatano, N. & Nelson, D. R. Localization transitions in non-Hermitian quantum mechanics. Phys. Rev. Lett. 77, 570 (1996).
Zhang, K., Yang, Z. & Fang, C. Correspondence between winding numbers and skin modes in non-Hermitian systems. Phys. Rev. Lett. 125, 126402 (2020).
Lee, J. Y., Ahn, J., Zhou, H. & Vishwanath, A. Topological correspondence between Hermitian and non-Hermitian systems: anomalous dynamics. Phys. Rev. Lett. 123, 206404 (2019).
Schindler, F., Gu, K., Lian, B. & Kawabata, K. Hermitian bulk-non-Hermitian boundary correspondence. PRX Quantum 4, 030315 (2023).
Franca, S., Könye, V., Hassler, F., van den Brink, J. & Fulga, C. Non-Hermitian physics without gain or loss: the skin effect of reflected waves. Phys. Rev. Lett. 129, 086601 (2022).
Okuma, N., Kawabata, K., Shiozaki, K. & Sato, M. Topological origin of non-Hermitian skin effects. Phys. Rev. Lett. 124, 086801 (2020).
Claes, J. & Hughes, T. L. Skin effect and winding number in disordered non-Hermitian systems. Phys. Rev. B 103, L140201 (2021).
Loring, T. A. K-theory and pseudospectra for topological insulators. Ann. Phys. 356, 383–416 (2015).
Liu, H. & Fulga, I. C. Mixed higher-order topology: boundary non-Hermitian skin effect induced by a Floquet bulk. Phys. Rev. B 108, 035107 (2023).
Cerjan, A., Koekenbier, L. & Schulz-Baldes, H. Spectral localizer for line-gapped non-Hermitian systems. Preprint at https://arxiv.org/abs/2303.09626 (2023).
Gong, Z. et al. Topological phases of non-Hermitian systems. Phys. Rev. X 8, 031079 (2018).
Yao, S. & Wang, Z. Edge states and topological invariants of non-Hermitian systems. Phys. Rev. Lett. 121, 086803 (2018).
Loring, T. A. A guide to the Bott index and localizer index. Preprint at https://arxiv.org/abs/1907.11791 (2019).
Michala, J., Pierson, A., Loring, T. A. & Watson, A. B. Wave-packet propagation in a finite topological insulator and the spectral localizer index. Involve J. Math. 14, 209–239 (2021).
Su, W. P. W., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698 (1979).
Ochkan, K. et al. Observation of non-Hermitian topology in a multi-terminal quantum Hall device. Zenodo https://doi.org/10.5281/zenodo.6985564 (2022).
Acknowledgements
We thank U. Nitzsche for technical assistance. J.D. would like to thank his departed friend and colleague F. Portier for introducing him to the physics of the quantum Hall effect. This work was supported by the French RENATEC network, by DIM NANO-K, by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy through the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter—ct.qmat (EXC 2147, project ids 390858490 and 392019), and by the European Union’s H2020 FET Proactive project TOCHA (No. 824140). L.V. was supported by the Leibniz Association through the Leibniz Competition.
Funding
Open access funding provided by Leibniz-Institut für Festkörper- und Werkstoffforschung Dresden (IFW).
Author information
Authors and Affiliations
Contributions
J.D. and I.C.F. conceived and supervised the project. J.D. and K.O. designed the sample, conducted the measurements and analysed the data with input from L.V. and R.G. D.M. fabricated the sample on GaAs/AlGaAs heterostructures grown by A.C. and U.G. R.C. performed the numerical simulations of the HN model, computed the PD invariant and developed the localizer index, under the supervision of V.K., E.M.H., J.v.d.B. and I.C.F. V.K. introduced the idea of iterative measurement and performed the numerical simulations showing their feasibility. All authors participated in interpreting the results and writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Eigenspectra and skin effect.
a, Eigenspectra for OBC and PBC. The eigenvalues are real for OBC, and complex for PBC. The arrow indicates the spectral winding expected in the Bloch Hamiltonian, with winding number w = + 1. b, SPD plotted against the sites of the system on a log-linear scale under OBC and PBC; We use (Jleft, Jright) = (2, 1) and a chain consisting of 100 sites.
Extended Data Fig. 2 Generated sine waves.
a, Randomly generated initial currents displayed on a unitary circle in polar coordinates for a 6-site OBC set-up. The radius and the angle correspond respectively to the amplitude Ai(0) and the phase ϕi(0) in Eq. (15). The lower panel shows the injected signal representing the different components of the vector for n = 0. b-f, Evolution of the signal throughout the steps of the iteration process.
Extended Data Fig. 3 All experimental power iteration runs.
a, Different final current vectors of the system, corresponding to different initial random vectors, displayed on a unitary circle in polar coordinates for a 6-site OBC set-up. The radius and the angle correspond respectively to the amplitude Ai(0) and the phase ϕi(0) in Eq. (15). Different colors represent different initial current vectors. The final current configurations are always in phase (regarding the different components of the vector) and always show a non-Hermitian skin effect. b, Plot of the standard deviation of the current vector as defined in Eq. (16) as a function of the iteration index for OBC c, Elements of the final currents injected into the system for a 6-site PBC set-up. d, Plot of the standard deviation of the current vector as defined in Eq. (16) as a function of the iteration index for PBC.
Supplementary information
Supplementary Information
Supplementary Sections 1–7 and Figs. 1–11.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ochkan, K., Chaturvedi, R., Könye, V. et al. Non-Hermitian topology in a multi-terminal quantum Hall device. Nat. Phys. 20, 395–401 (2024). https://doi.org/10.1038/s41567-023-02337-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-023-02337-4
This article is cited by
-
Classifying topology in photonic crystal slabs with radiative environments
npj Nanophotonics (2024)