Spontaneous self-constraint in active nematic flows

Abstract

Active processes drive biological dynamics across various scales and include subcellular cytoskeletal remodelling, tissue development in embryogenesis and the population-level expansion of bacterial colonies. In each of these, biological functionality requires collective flows to occur while self-organised structures are protected. However, the mechanisms by which active flows can spontaneously constrain their dynamics to preserve structure are not known. Here, by studying collective flows and defect dynamics in active nematic films, we demonstrate the existence of a self-constraint, namely a two-way, spontaneously arising relationship between activity-driven isosurfaces of flow boundaries and mesoscale nematic structures. We show that self-motile defects are tightly constrained to viscometric surfaces, which are contours along which the vorticity and the strain rate are balanced. This in turn reveals that self-motile defects break mirror symmetry when they move along a single viscometric surface. This is explained by an interdependence between viscometric surfaces and bend walls, which are elongated narrow kinks in the orientation field. These findings indicate that defects cannot be treated as solitary points. Instead, their associated mesoscale deformations are key to the steady-state coupling to hydrodynamic flows. This mesoscale cross-field self-constraint offers a framework for tackling complex three-dimensional active turbulence, designing dynamic control into biomimetic materials and understanding how biological systems can employ active stress for dynamic self-organisation.

Main

Disorderly turbulent flows occur in many classes of fluids, and characterising their inertial turbulence¹ remains an outstanding challenge due to their chaotic nature across spatial and temporal scales². However, the challenges are compounded in rheologically complex fluids because couplings between fields introduce additional nonlinearities. In elastic², granular³, magnetohydrodynamic⁴, quantum⁵ and liquid crystalline⁶ turbulence, velocity is strongly coupled to other fields, some of which have their own topologies with associated defects^7,8,9. There is growing evidence that many biological systems spontaneously exhibit turbulence-like disorderly flow states that are coupled to local orientation (nematic) fields^10,11. In these systems, active turbulence¹² is accompanied by the continual creation and annihilation of topologically protected defects in the orientational field, including self-propelled +1/2 defects in two dimensions¹³ and disclination lines in three dimensions¹⁴.

To simplify the complexities of active nematic flows, studies often prioritise one of the fields. Namely, since self-motile defects have been clearly identified as crucial to active turbulence, they are often viewed as controlling their own dynamical evolution, with only perturbations—either due to local deformations or neighbouring defects—causing deviations from their ideal trajectories^15,16,17. From this perspective, hydrodynamic flows follow directly from the governing defect configuration. The antithetical approach is to integrate the orientational field dynamics directly into the hydrodynamic stresses, thus creating defect-free fluid dynamical models^18,19,20. Such velocity-fixated studies focus on long-lived and spatially extended structures in the velocity and vorticity fields and attempt to identify scaling laws for the energy and enstrophy spectra²¹. Together, these two approaches have made substantial progress towards understanding active turbulence, but the crucial mesoscale bridge between them remains to be developed.

In this article, we reveal that nonlinear coupling between flow and orientational fields in active nematics leads to a strong, two-way, spontaneous self-constraint. On the one hand, we report that self-motile topological defects are tightly constrained to specific flow boundaries, whereas, on the other hand, these surfaces are driven by mesoscale defect-associated nematic deformations. Specifically, our results demonstrate that self-motile +1/2 defects are found solely on specific isosurfaces of flow boundaries identified as viscometric surfaces, which are contours along which the vorticity and the strain rate are in balance. These surfaces dictate the evolution of the self-motile topological defects, which align with and move along the contours, as there is no deformation of the streamlines along these paths. We uncover how this causes the defects to break their ideally predicted mirror symmetry, and we classify them according to their handedness. However, the spontaneous self-constraint is a codependency, and we find that the viscometric surface, in turn, follows the mesoscopic deformation network of the orientational field. Although we focus on two-dimensional (2D) extensile active nematic turbulence, our conclusions hold whenever activity couples to plus-half-integer topological defects, such as in vortex lattices, flow-tumbling liquid crystals, contractile active stress, friction-induced ordering and three-dimensional (3D) structures. The generality of these perspectives may provide greater insights into a more universal understanding of fluidic systems with nonlinear field couplings and topologically protected states and may suggest a mechanism by which biological morphology could be dynamically protected.

Executive summary of experiments and simulations

To explore the spontaneous self-constraint between disclinations and flow structures in active nematics, we employ a combination of experimental and numerical techniques. Experimentally, we create an active nematic film by self-assembling labelled filamentous microtubule bundles at an oil–water interface with kinesin motor clusters²², which act as crosslinkers and hydrolyse adenosine triphosphate (ATP) suspended in the aqueous phase, fuelling extensile active stresses in the microtubule film (section ‘Experiments’). Microtubule bundles are imaged with confocal fluorescence microscopy, which allows the nematic tensor field Q to be inferred through coherence-enhanced diffusion filtering²³. The velocity field u is extracted with an optical flow method. Numerically, we simulate active nematohydrodynamics with a hybrid lattice Boltzmann approach²⁴ (section ‘Simulations’). We focus on 2D extensile nematics in steady-state active turbulence, which give rise to disorderly flow profiles and continuous defect creation and annihilation (Fig. 1 and Supplementary Video 1).

Fig. 1: Plus-half topological defects reside on isolines of ${{{\mathcal{Q}}}}=0$.

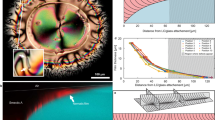
a, Scanning confocal microscopy of experimental active film (section ‘Experiments’). Plus-half defects are marked as green comet-shaped symbols and minus-half defects by dark blue trefoil-shaped symbols (section ‘Defect analysis’). The zero-isolines of the ${{{\mathcal{Q}}}}$ criterion are shown as solid lines coloured by the handedness of the enclosed vortex: red for clockwise and blue for anticlockwise (section ‘$\mathcal{Q}$ criterion’). Scale bar, 100 μm. b, Numerical simulations of active turbulence (section ‘Simulations’). The circulation of each vortex is coloured to represent the vortex strength. The nematic director field is plotted as a grey line field. c, Probability distribution function (PDF) of nearest distances of ±1/2 defects to the ${{{\mathcal{Q}}}}=0$ boundary (section ‘Defects and viscometric surfaces’). Expt., experimental; Sim., simulation. d, Experimental snapshots of pair-creation event in a microtubule/kinesin film. e, Experimental snapshots of a pair-annihilation event. f, Same snapshot as b but the vorticity field is coloured instead. Grey arrows indicate the velocity field. Zero-vorticity contours are shown as lilac dashed-dotted lines (section ‘Comparing zero-isosurfaces ${\mathcal{Q}}$ with vorticity’). Left, examples where the vorticity is non-zero (top) and zero (bottom) at a +1/2 defect position.

To explore the interplay between topology and flow, we calculate mesoscopic structures in each field. Defects are readily apparent (Fig. 1), and their positions and orientation are found from the nematic field Q (section ‘Defect analysis’). Likewise, active flow fields have a mesoscale structure with well-studied vorticity scales, which are visualised using the ${{{\mathcal{Q}}}}$ criterion²⁵:

$${{{\mathcal{Q}}}}=\frac{1}{2}\left(\|{\varOmega}\|^{2}-\|{E}{\|}^{2}\right),$$

(1)

where Ω and E are the vorticity and strain-rate tensors (section ‘Simulations’). Vorticity-dominated regions are identified by ${{{\mathcal{Q}}}} > 0$, whereas ${{{\mathcal{Q}}}} < 0$ in strain-rate-dominated regions (section ‘$\mathcal{Q}$ criterion’). This technique has been used to identify vortex structures in confluent cell layers²⁶, but any quantitative interplay between disclination positions, the $\mathcal{Q}$ criterion and director structure is not yet fully understood.

Plus-half defects are constrained to viscometric surfaces

By partitioning flow domains into vorticity-dominated (${{{\mathcal{Q}}}} > 0$) and strain-rate-dominated (${{{\mathcal{Q}}}} < 0$) flow, we confirm the previously reported qualitative observation that defects tend to be found near the edge of vortices^25,27. However, by imaging ${{{\mathcal{Q}}}}=0$ isolines (section ‘$\mathcal{Q}$ criterion’), we identify that +1/2 defects are found on the border where ${{{\mathcal{Q}}}}=0$ with the probability of finding a +1/2 defect decaying exponentially with distance from the isosurface, decreasing orders of magnitude over a fraction of the active length scale (Fig. 1c). We refer to the lines of ${{{\mathcal{Q}}}}=0$ as viscometric surfaces, as these are points where the velocity gradient tensor is singular and nilpotent, indicating simple shear flow (section ‘$\mathcal{Q}$ criterion’). In the experimental system (Fig. 1a and Supplementary Video 1), roughly 100 defects are in frame and all the +1/2 defects are on viscometric surfaces (solid lines coloured by the handedness of the enclosed vortex) at all times. The viscometric surfaces enclose vorticity-dominated regions, which exhibit a broad distribution of sizes, shapes and circulation (Extended Data Fig. 1). Simulations reveal that ${{{\mathcal{Q}}}}=0$ contours that have an associated +1/2 defect tend to enclose vortices with larger circulation (Fig. 1b and Supplementary Video 2). Both experiments and simulations demonstrate that, whereas +1/2 defects are constrained to viscometric surfaces, −1/2 defects are not (Fig. 1c). Defect pair-creation and pair-annihilation events occur on ${{{\mathcal{Q}}}}=0$ boundaries (Fig. 1d,e), with the motile +1/2 defect pinned to the ${{{\mathcal{Q}}}}=0$ viscometric surface throughout the process, whereas the −1/2 defects are unbound from the ${{{\mathcal{Q}}}}=0$ lines.

Previous studies observed that defects reside near the edges of vortices^25,27, but the implications have not been quantified. Commonly, active flow states are visualised by their vorticity field (Fig. 1f and Supplementary Video 3). Although these visualisations demonstrate the importance of vorticity in the characteristic active length and timescales, they are not observed to strictly constrain the configuration of defects. By identifying edges of vortices as the point where the direction of the vorticity ω inverts (section ‘Comparing zero-isosurfaces $\mathcal{Q}$ with vorticity’), it is seen that most but not all +1/2 defects exist for ∣ω∣ = 0 (Fig. 1f, dashed-dotted lines). Although this agrees with previous statements that defects tend to sit near the edges of vortices^25,27, our experiments and simulations demonstrate that this is not a strict colocalisation constraint, as not every +1/2 defect sits on zero-vorticity contours (Fig. 1f, top inset), as quantified by comparing the distribution of distances to ${{{\mathcal{Q}}}}=0$ or ∣ω∣ = 0 (Extended Data Fig. 7). Thus, it is not only where the vorticity is zero but rather where the vorticity and strain rate balance to produce simple shear.

As a result, in both experimental and simulated results, +1/2 nematic defects reside directly on this flow boundary (Fig. 1c). Likewise, −1/2 nematic defects are also most likely to be found on ${{{\mathcal{Q}}}}=0$; however, this is because they are initially created at ${{{\mathcal{Q}}}}=0$ due to the constraint on their +1/2 partner. In contrast to +1/2 defects, −1/2 defects are not constrained to remain on specific flow contours and can be associated with any value of ${{{\mathcal{Q}}}}$—they exist in both strain-rate- and vorticity-dominated regions (Fig. 2a). Thus, they have a wider range in their distance distribution (Fig. 1c). Indeed, the ideal picture of a solitary −1/2 defect is not located on ${{{\mathcal{Q}}}}=0$, but instead is encircled by a floweret of six vortices of alternating handedness (Fig. 2b, section ‘Stokesian solitary-defect model’, ref. ²⁸). As a result, −1/2 defects reside in places with any sign of the ${{{\mathcal{Q}}}}$ criterion (Fig. 2a and Supplementary Video 2). In contrast, the striking coincidence of +1/2 defects on ${{{\mathcal{Q}}}}=0$ flow contours suggests an intrinsic relationship between flow structures and the trajectory of the self-propelled defects.

Fig. 2: Configurations of defects and viscometric surfaces.

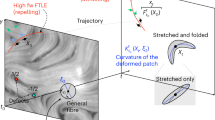
a, Snapshot of the flow geometry around −1/2 and +1/2 nematic defects from the numerical simulations, illustrating three −1/2 defects in a strain-dominated region, in a vorticity-dominated region and on the ${{{\mathcal{Q}}}}=0$ border. Arrows show the instantaneous velocity field, dashed lines the director field and solid lines the ${{{\mathcal{Q}}}}=0$ contours, with the enclosed area coloured by circulation (red for clockwise and blue for anticlockwise). Blue trefoil symbols mark −1/2 defects and green comet-shaped symbols represent +1/2 defects. b, Prediction for ideal, solitary −1/2 defect (section ‘Stokesian solitary-defect model’). c–e, Snapshots of +1/2 defects for mirror symmetry (c) and broken mirror symmetry with an anticlockwise vortex (d) or clockwise vortex (e). f, Same as b for a solitary +1/2 defect. g, PDF of alignment angles between the defect orientation and the tangent of the associated viscometric (${{{\mathcal{Q}}}}=0$) line (section ‘Defects and viscometric surfaces’). The vertical blue dashed-dotted line indicates the ideally expected alignment from f (section ‘Stokesian solitary-defect model’). The grey dashed line indicates the alignment angle for a point active force (section ‘Stokesian line-force model of bend walls’).

Self-constraint violates ideal view of defect-generated flow

Investigating the relationship between the viscometric (${{{\mathcal{Q}}}}=0$) surfaces and the +1/2 defect positions reveals that the defect/surface complexes exist in two distinct configurations. Either a +1/2 defect is positioned at an intersection of viscometric lines (Fig. 2c), or a defect lies parallel to a single ${{{\mathcal{Q}}}}=0$ viscometric line (Fig. 2d,e). In the first case (Fig. 2c), a +1/2 defect is positioned at a crossroads between two viscometric lines and has two equally strong counter-rotating vortex regions on either side of the defect axis, whereas the flow directly in front and behind is strain-rate dominated. Thus, the defect has a mirror symmetry along its head–tail axis. This corresponds to the ideal picture of a solitary defect (Fig. 2f, section ‘Stokesian solitary-defect model’, ref. ²⁸), which is tacitly the expectation of flows around defects in active turbulence. The combination of these flow geometries ensures the velocity field flows parallel to the defect orientation and self-propulsion direction. However, this mirror-symmetric configuration is transient. Although the ideal model of solitary defects describes how active forces are a symmetric source of vorticity on both sides of the defects, in experiments and simulations, actual vorticity-dominated regions are not self-propulsively moving alongside self-motile defects as the picture might suggest.

Instead, the mirror symmetry around the isolines is broken (Fig. 2d,e). Each of the defects in these states orient parallel to a single viscometric line, with vorticity dominating on one side and the strain rate dominating on the other. This spontaneous handedness of a subpopulation of defects is not predicted by the ideal model for a solitary defect; however, defects with this configuration persist for long durations and are observed to be the majority (Fig. 1 and Supplementary Video 2) because a motile defect can persistently move along the ${{{\mathcal{Q}}}}=0$ line, circulating around a single neighbouring vortex. As a result, local chirality spontaneously emerges in this globally achiral system. This spontaneous handedness is necessarily erased when averaging fields around defect cores for an ensemble. The average flow profiles of the two non-symmetric cases are distinct from the mirror-symmetric case when the subpopulations are separately averaged (Extended Data Fig. 2). Thus, Fig. 2f must be reinterpreted as an idealisation rather than an expectation.

We quantify the nature of these defect/viscometric surface complexes through the distribution between the defect alignment angles between the +1/2 defect axis and the ${{{\mathcal{Q}}}}=0$ boundary tangent (Fig. 2g; section ‘Defects and viscometric surfaces’). In experiments and simulations, the most likely alignment is directly parallel. In contrast, the ideal solitary-defect theory predicts that the +1/2 defect is oriented at 35° from the two side viscometric contours. We find that the measured angle is often smaller than the ideal-model angle. This further demonstrates that the broken-mirror-symmetry configuration is actually preferred to the symmetric configuration predicted by the ideal solitary-defect theory (section ‘Stokesian solitary-defect model’).

Disclinations intermittently transform between the mirror-symmetric and the broken-mirror-symmetry cases (Supplementary Video 2). The results so far evidence that specific isolines of flow boundaries constrain the motion of topological defects, but, in the next section, we show that there is a two-way interdependence and explain by what mechanism defects and viscometric contours are pinned.

Bend walls and viscometric surfaces are interdependent

Although active forcing is often assumed to be localised to the immediate vicinity of topological singularities (section ‘Stokesian solitary-defect model’), more generally, an active force is generated by any deformation of the orientation field (section ‘Simulations’). In particular, bend walls play an essential role in extensile active nematics²⁹. Bend walls are narrow lines of high bend deformation that form sharp kinked lines between nematic domains. They represent a nematic Néel wall³⁰ or an elasticity band³¹. As highly localised deformations, bend walls generate strong active forcing. Because extensile nematics are hydrodynamically unstable³², a bend constricts into system-spanning narrow kink lines in initially ordered systems before defect pairs unbind along the walls and the self-motile +1/2 defects unzip the bend wall as it advances³³. After this initial development of active turbulence, it is then presumed that substantial forces occur only in the immediate vicinity of defects. However, in practice, this is not observed in experiments or simulations. Rather, the hydrodynamic instability incessantly constricts a bend into sharp kink walls, as demonstrated by the splay-bend parameter S_SB, which indicates splay and bend deformations (section ‘Splay-bend parameter’). The splay-bend parameter traces bend walls through strongly negative S_SB values (Fig. 3a and Supplementary Video 4), revealing that bend walls are correlated strongly with the ${{{\mathcal{Q}}}}=0$ viscometric lines. The distribution of S_SB coinciding with viscometric surfaces is more skewed towards negative (bend) values than for the system as a whole (Fig. 3b).

Fig. 3: Viscometric surfaces generated by bend walls.

a, Same snapshot as Fig. 1b with colour map corresponding to the scalar splay-bend parameter S_SB (section ‘Splay-bend parameter’). Narrow lines of strong negative S_SB are interpreted as bend walls. b, PDF of S_SB sampled equally for all points and times and the PDF of S_SB only on ${{{\mathcal{Q}}}}=0$ contours. c–e, ${{{\mathcal{Q}}}}$ criterion and velocity field predicted by the Stokesian line-force model of bend walls (section ‘Stokesian line-force model of bend walls’). Red and blue shading indicates clockwise and anticlockwise vorticity-dominated regions. The white regions are strain-rate dominated. The ${{{\mathcal{Q}}}}=0$ contours are solid lines. The unit-vector velocity fields are shown with grey arrows. The line forces are shown as solid purple lines with the direction of forcing indicated by the purple arrows. The start and end points of the force lines are represented by green and blue circles, respectively. Forces are constructed as a point source (c), a finite straight line (d) or a circular arc (e).

The extended concurrence of bend walls and ${{{\mathcal{Q}}}}=0$ lines suggests that elongated bend walls are crucial for defect dynamics and viscometric surface cross-constraints. To understand the nature of the flows associated with bend walls, we first consider prescribing a director field and solving the resulting active flow. We find that a repeating series of infinitely long, perfectly straight bend/splay structures is consistent with ${{{\mathcal{Q}}}}=0$; however, fixed straight bend walls produce ${{{\mathcal{Q}}}}=0$ everywhere, rather than just in the immediate vicinity of the bend wall (section ‘Stokesian straight bend-wall model’). This is because perfectly straight, infinitely long bend walls produce only shear stress, for which the vorticity and strain rates are balanced. Bend-wall curvature is added by perturbing the bend walls into infinitely long sinusoidal undulations (section ‘Wavy bend-wall model’), which numerically demonstrates that curved bend walls produce closed viscometric surfaces (Extended Data Fig. 3a,b). Furthermore, by then fixing the flow and allowing the director to reach a steady state, we show numerically that active viscometric flows drive additional bend constriction, narrowing the bend walls into kink lines but not further perturbing their conformation (Extended Data Fig. 3c,d). This re-emphasises an essential property: ${{{\mathcal{Q}}}}=0$ lines, where the vorticity and strain rate balance, are also where the velocity gradients exhibit no stretching or elongation of equidistant streamlines. This is not only why ${{{\mathcal{Q}}}}=0$ is referred to as ‘viscometric’ but also why the bend walls are not further perturbed by the flows and why flows do not misalign defects from following ${{{\mathcal{Q}}}}=0$ lines. Thus, this simple model suggests that for the bend walls to be deformed, they cannot be infinitely long.

Physical model

To understand how these mesoscale nematic and hydrodynamic structures are intertwined, we systematically consider step-by-step extensions of the idealisation of defects as solitary points. These simple steps iteratively demonstrate that defects cannot be treated as isolated points but must be considered in conjunction with mesoscale defect/kink-wall structures. This model explains the interdependence of viscometric contours and the handedness of bound +1/2 defects arising in active nematics. We assume that active stresses constrict bend into narrow structures (Extended Data Fig. 3) and dominate elastic stresses, allowing us to approximate the flows using the Stokes equation (section ‘Stokesian line-force model of bend walls’). By solving the Stokes equation, we calculate the velocity field and ${{{\mathcal{Q}}}}=0$ contours for the following cases: (1) an isolated point, (2) a finite straight line and (3) a curved line (Fig. 3c–e):

• Case (1): Consider a simple point-force model of a solitary defect. In agreement with the ideal analytical solution of a solitary +1/2 defect (Fig. 2f), modelling defects as simple point forces is sufficient for qualitatively predicting the mirror-symmetric configuration at intersections (Fig. 3c). However, neither is capable of predicting the handed configuration nor the observed distribution of intersection angles because defects are associated with narrow kink walls, even in steady-state turbulence.

• Case (2): To account for bend walls as simply as possible, the model must recognise that deformations and the associated active force density localise along the narrow bend walls, and so it treats defect/bend-wall complexes as finitely long, straight force lines (Fig. 3d). This model predicts a more acute angle between the ${{{\mathcal{Q}}}}=0$ contours and the defect axis, improving on case (1) but not resolving the essential inability to predict handed configurations (Fig. 2).

• Case (3): There is an additional complication: kink walls do not remain straight. Due to the inherently unstable nature of the extensile active nematics, bend walls continuously curve (Supplementary Video 4). Introducing curvature into the model by considering a circular arc of active forcing (Fig. 3e) results in the upper, anticlockwise ${{{\mathcal{Q}}}}=0$ contour separating from the bend wall, whereas the lower, left-handed ${{{\mathcal{Q}}}}=0$ isoline colocalises along the bend wall. Hence, defects modelled as the singular ends of finitely long, curved kink walls produce the broken-symmetry case with a vorticity-dominated flow on one side and a strain-rate-dominated-flow on the outside of the bend wall.

Hence, the straightforward model of a finite, curved force line explains how bend walls play the crucial role in realising the interdependence of defect dynamics and viscometric surfaces. First, bend constriction due to hydrodynamic instability causes active forces to be localised along narrow lines, resulting in shearing flows that neither stretch nor elongate the streamlines. Self-motile +1/2 defects unzip these narrow bend walls as they preferentially move along them and, thus, are elastically constrained to ${{{\mathcal{Q}}}}=0$. Finally, the finite length and curvature of the bend walls causes the broken-mirror-symmetry case, demonstrating that the broken symmetry is not simply due to random interactions and torques from the isotropic active turbulence.

Although simple, this model allows us to make novel predictions about defect dynamics. For instance, it has long been noticed that pair-creation events occur somewhere along extended bend walls^33,34, but predicting the creation site has not previously been possible; however, our simple model immediately allows us to identify where pair-creation events will occur along bend walls, namely along S_SB lines where ${{{\mathcal{Q}}}}=0$ isolines converge (Extended Data Fig. 4). The model also makes predictions about a defect’s future trajectory without any non-local information about the flow or director field. As broken-mirror-symmetry defects continue to move around their associated vortex edge along a curved bend wall, the instantaneous handedness of the defect reveals the direction its trajectory is likely to curve along (Extended Data Fig. 5). Furthermore, the model relies on the curvature of kink walls due to the hydrodynamic instability of wet active nematics. This intimates that +1/2 defects in dry active nematic systems are predicted to maintain mirror symmetry and be pinned to viscometric intersections, as verified by a reinterpretation of numerical simulations³⁵. At intermediate friction (Extended Data Fig. 8a), we observe subpopulations of defects that exist only in the handed state, from which they cannot escape. This results in two bounded +1/2 spiral defects rotating around each other. Eventually, in the limit of strong isotropic drag (Extended Data Fig. 8b), this state dominates, resulting in the ordered defect states found in dry nematics.

Beyond extensile, flow-aligning 2D active nematic turbulence

This study has focused on the spontaneous self-constraint between defects and flow structures in unconfined 2D extensile nematic turbulence. However, our evidence suggests that this phenomenon is substantially more general, apparently holding whenever +1/2 topological defects are present in active nematics (Fig. 4).

Fig. 4: The spontaneous self-constraint between motile +1/2 defects and viscometric surfaces holds more generally.

a–e, Numerical simulations of 2D active nematics, with colour maps, lines and markers the same as in Fig. 1b. a, Active extensile turbulence with an alignment parameter in the flow-tumbling regime. b, Contractile active turbulence in an operating regime with rare instances of bound +1/2 defect pairs creating effective +1 defects, which do not need to be on ${{{\mathcal{Q}}}}=0$. Same S_SB visualisation as Fig. 3a. c, Lanes of alternating circulation form with anisotropic friction in the flow-aligning regime. d,e, Dancing defect dynamics in a 2D confining channel, with +1/2 defects switching between vortices and at ${{{\mathcal{Q}}}}=0$ intersections (d) and aligned along vortex boundaries (e). f, Experimental verification that the spontaneous self-constraint is retained in a confined channel. Scale bar, 100 μm. g, 3D vortex lattice with disclinations coloured by the twist angle ($\cos \beta$ from section ‘Defect analysis’). Yellow indicates a local +1/2 wedge profile, green a twist-type profile and blue a −1/2 wedge profile. Grey shading illustrates vorticity-dominated regions (${{{\mathcal{Q}}}} > 0$), and white where the strain rate dominates (${{{\mathcal{Q}}}} < 0$).

The conclusions arrived at for flow-aligning active turbulence also hold in the flow-tumbling (Fig. 4a) and intermediate regimes, with no change to the likelihood of finding +1/2 defects away from ${{{\mathcal{Q}}}}=0$ isolines (Extended Data Fig. 7b). Once again, defects reside on viscometric contours, and either travel along a single vortex boundary or transiently cross an intersection (Supplementary Video 5). The interdependence strongly resembles the flow-aligning regime, which is consistent with the expectation that active turbulence behaves similarly in flow-aligning and flow-tumbling regimes. Furthermore, the conclusions likewise generally hold for contractile activity (Fig. 4b). Minus-half defects are still non-motile and unbound from viscometric lines. Motile +1/2 defects now chase their tail (move in the opposite direction compared to extensile defects) and unzip splay walls; yet, they are still most likely to be found self-propulsively moving where ${{{\mathcal{Q}}}}=0$ (Supplementary Video 6). However in flow-aligning contractile systems, there is an intriguing exception. In a narrow parameter regime, a pair of similarly charged +1/2 defects can temporarily form metastable +1 complexes³⁶. These effectively immotile +1 complexes produce a flow profile that does not necessitate ${{{\mathcal{Q}}}}=0$, and thus, these effectively +1 compounds do not reside where ${{{\mathcal{Q}}}}=0$, allowing them to briefly elude the confinement condition. Thus, the motility of +1/2 defects, which actively unzip deformation walls, is central to the reported interdependence.

How robust is the interdependence between +1/2 defects and ${{{\mathcal{Q}}}}=0$ to frictional screening? Homogeneous friction, for example, can modify the properties of active turbulence^37,38 and anisotropic friction can order flow states^39,40. Anisotropic friction creates an easy flow axis to form lanes with preferred circulation handedness encircled by ${{{\mathcal{Q}}}}=0$ (Fig. 4c and Supplementary Video 7). The vortex-dominated regions form a lattice of viscometric contours, with intersection points along the boundary at advective lanes. Defects still reside on ${{{\mathcal{Q}}}}=0$ and, moreover, now appear to be predominantly found on intersections, as was the case for isotropic friction (Extended Data Fig. 8). This suggests a distinction between the low- and high-friction regimes: defects are more likely to be in the broken-mirror-symmetry configuration without friction, whereas high-friction regimes combat bending curvature and instabilities, which our theoretical model suggests will make mirror-symmetric defects more likely. Another test is to allow the activity to go to zero. In that case, the self-constraint holds during the transient dynamics of quenched passive nematics that are generating non-zero backflow while relaxing through defect annihilation (Supplementary Video 10). However, unlike the active case, +1/2 defects are overwhelmingly found at ${{{\mathcal{Q}}}}=0$ intersections (Extended Data Fig. 9a,b), which is to be expected from ‘Physical model’. Without activity to produce elongated, curved kink walls, deformations are primarily in the immediate vicinity of defects and the simple point-force model (case (1)) predicts mirror-symmetric defects.

Impermeable, no-slip boundary conditions can also have profound effects on spontaneous active flow states by creating complex spatio-temporally ordered dynamics, even in simple geometries, such as a confined 2D channel^27,41. The resulting vortex lattice and associated defect dancing is clear in the simulations (Fig. 4d,e and Supplementary Video 8) and also apparent in the experiments (Fig. 4f and Supplementary Video 9). In both simulations and experiments, the +1/2 defects orient parallel to the viscometric line when traversing a vortex (Fig. 4e) and are able to cross to neighbouring vortices by passing through the fleeting ${{{\mathcal{Q}}}}=0$ intersection (Fig. 4d and Supplementary Video 11). Similarly, in experiments, +1/2 defects weave through the centre, traversing to neighbouring vortices through viscometric intersections. These dancing dynamics beautifully illustrate the transitions between the mirror-symmetric and broken-mirror-symmetry configurations (Extended Data Fig. 6). Plus-half defects orient and travel parallel to the edge of a vortex, until two vortices instantaneously touch to form a short-lived ${{{\mathcal{Q}}}}=0$ intersection, which allows the defects to transfer to the next vortex of opposite handedness. All the while, the defects remain on the ${{{\mathcal{Q}}}}=0$ lines.

In fact, the interdependent spontaneous self-constraint holds in 3D, in which point defects become disclination lines and viscometric contours become 2D surfaces. The vortex lattice exists in a 3D duct⁴². Analogously to the 2D case, wedge-type −1/2-profile disclination lines exist at the walls, whereas disclinations with a wedge-type +1/2 profile dance around the central vortex lattice (Fig. 4g). The disclinations at the centre with wedge-type +1/2 profiles continually maintain contact with the 2D ${{{\mathcal{Q}}}}=0$ isosurfaces (Supplementary Video 12), demonstrating that motile defects are constrained to lie on ${{{\mathcal{Q}}}}=0$ surfaces even in 3D. Altogether, the examples explored in Fig. 4 indicate that the self-emergent constraint between motile defect dynamics and viscometric surfaces is not only a property of extensile active turbulence but, more generally, apparently holds whenever motile defects are present in active nematics.

Conclusion

In conclusion, we have identified and explained a spontaneously arising constraint between defect dynamics and viscometric surfaces for which the vorticity and the strain rate balance. Although previous insights noted that defects tend to be found near the edge of vortices²⁵, our results quantify this not as a tendency but as a fundamental spontaneous self-constraint between defects and coherent flow structures. It is observed not just in active turbulence but in any defect-laden active nematic system. This work challenges the idea that nematic defects are solely responsible for their own dynamics. Ultimately, neither defects nor hydrodynamics alone govern the multi-field dynamics that spontaneously arises in active nematics. Rather, the defects and the hydrodynamics are intrinsically interdependent. Identifying this spontaneous self-constraint has revealed that viewing solitary self-motile defects as generating pairs of mirror-symmetric vortices that remain at their sides must be contextualised as an idealisation that corresponds to a subset of +1/2 defects over a limited duration rather than the expectation for all defects at all times. Instead, motile defects more often move along a single viscometric surface, where there is no stretching nor elongation of the fluid, which appears to hold for all motile defects in active nematics and not only 2D extensile active turbulence. This shows that defects can be classified into three conformations based on local handedness with respect to their viscometric surface surroundings. Until now, this distinction, together with any difference in emerging dynamical behaviour, has been neglected. Not only do the hydrodynamics not force the +1/2 defects off these contours, but it coincides with the very bend walls that these defects are unzipping, showing that the field dynamics are codependent. These results underscore the continual role of bend-wall constriction and unzipping in steady-state dynamics. Active nematic defects cannot be viewed as points but are one component of mesoscale nematic structures. Our work highlights the centrality of mesoscale structure in collective dynamics. It may provide a mechanism for manipulating the degree of orderly dynamics in a system, suggest potential new avenues for exploring topological entropy⁴³ and prove an imperative fact for hydrodynamic descriptions of active defect gases^11,15.

We anticipate that our observation of codependence will complement recently developed Lagrangian descriptions of coherent structures⁴⁴ and aid efforts to understand the highly complicated structure of 3D active turbulence⁴⁵ by potentially reducing the information from several 3D vector fields to isosurfaces of scalar invariants of the velocity gradient and topologically protected disclination lines. Future work might consider differences between how small defect loops and long tangled defect lines⁴⁶ interact with viscometric surfaces or how these isosurfaces are related to transformations between positive winding, negative winding and twisted profiles⁴⁷. The self-constraint identified here could lead to designs for novel active functionality^48,49 or biointerfaces⁵⁰. Tracking viscometric surfaces embedded on curved surfaces may be a new pathway for studying the relationship between topology and dynamics^23,51,52,53, as it may illuminate the potential connections between defects and active flow in morphodynamics⁵⁴. Biological systems, including active transport in microbial colonies⁵⁵, mitotic spindle assembly⁵⁶, tissue responses⁵⁷, epithelial reorganisation⁵⁸ and morphogenesis⁵⁹, all involve a careful balance between collective motion and protected structures for their functionality. Ultimately, spontaneous constraints in active materials could have far-reaching implications for understanding how biological systems utilise active stresses for simultaneous dynamics and restraint.

Methods

Experiments

Materials

Short and stable microtubules were polymerised by incubating, at 37 °C for 30 min, a mixture containing 8 mg ml⁻¹ of recycled tubulin from bovine brain (Brandeis Materials Research Science and Engineering Center), 6 mM of guanosine-5′-[(α,β)-methyleno]triphosphate (NU-405S, Jena Biosciences) and 1 mM of dl-dithiothreitol (DTT; 43815, Sigma) in M2B buffer (80 mM of PIPES (P1851, Sigma), 1 mM of EGTA (E3889, Sigma) and 2 mM of MgCl₂, pH = 6.8). After incubation, the solution was kept at room temperature for 5 h, then frozen in liquid nitrogen and stored at −80 °C for future use. For the confocal fluorescence microscopy, 3% of the tubulin was labelled with Alexa-647, a bright, far-red-fluorescent dye. Biotinylated kinesin was prepared in the BioNMR group at the Institute of Bioengineering of Catalunya. Drosophila melanogaster heavy-chain kinesin-1 K401-BCCP-6His was expressed in Escherichia coli using the plasmid WC2 from the Gelles Laboratory (Brandeis University). Biotinylated kinesins were purified with a nickel column and dialysis against 500 mM imidazole aqueous buffer. The kinesin concentration was estimated at 2.5 μM by absorption spectroscopy. It was finally stored in a 40% w/v sucrose solution at −80 °C for future use. Kinesin clusters were obtained by preparing a mixture with 1 μM of biotinylated kinesin dimers and 31 μg ml⁻¹ of tetrameric streptavidin in a M2B buffer supplemented with 0.2 mM of DTT, this stoichiometric ratio corresponding approximately to two kinesin dimers per cluster. This mixture was incubated on ice for 30 min.

The active microtubule/kinesin gel consisted in a M2B preparation with 1.6 mg ml⁻¹ of microtubules, motor clusters (the concentration of streptavidin was 8.2 μg ml⁻¹), 1.4 mM of ATP (A2383, Sigma) to fuel the molecular motors and 1.6% w/v of depleting agent polyethylene glycol (20 kDa, 9517, Sigma) to induce the bundling of the microtubules. An ATP-regenerating system (2.8% v/v of pyruvate kinase/lactate dehydrogenase (P02, Sigma) and 26.2 mM of phosphoenolpyruvate (P7127, Sigma)) was employed to keep a fixed concentration of ATP during the experiments. To prevent photobleaching and oxidation, some antioxidants were included in the active gel: 5.4 mM of DTT, 3.3 mg ml⁻¹ of glucose (G8270, Sigma), 38 μg ml⁻¹ of catalase (C40, Sigma), 0.22 mg ml⁻¹ of glucose oxidase (G2133, Sigma) and 2.0 mM of trolox (238813, Sigma). The MgCl₂ concentration was raised with 4.7% v/v of a mix solution (69 mM of MgCl₂ in M2B). The pH of the active gel was adjusted to 6.8.

Active nematic assembly

Active nematic layers were assembled at a water/oil interface following two different protocols. The unconfined active nematic layer (as shown in Fig. 1a) was prepared in a closed observation chamber. The latter had a bottom hydrophobic glass slide treated with Aquapel. A hydrophilic coverslip coated with a polyacrylamide brush separated by 120 μm of double-sided tape was used to form a rectangular chamber of size 3 mm × 22 mm. The chamber was first filled with fluorinated oil (HFE7500) with 1.8% v/v of 008-FluoroSurfactant (RAN Biotechnologies). Then 10 μl of the active gel was introduced by capillarity into the chamber, which replaced most of the oil. A lubricating film of oil remained on the surface of the bottom glass slide. The chamber was sealed with UV-curable glue (Norland NOA-81). The assembly of the microtubule bundles at the water/oil interface was subsequently sped up by centrifuging the sample for 10 min at 215g. For laterally confined active nematics (as shown in Fig. 4f), we prepared an open observation chamber by sticking circular polydimethylsiloxane walls (1 cm in diameter) to a polyacrylamide-coated glass slide with UV-curable glue. Then, 2.5 μl of the active gel supplemented with 4.6 μg μl⁻¹ of pluronic F-127 surfactant (Sigma, P-2443) was deposited in the well and spread over the hydrophilic glass surface and then immediately covered with 200 μl of silicone oil with a dynamic viscosity of 20 mPa s. The assembly of the microtubule bundles at the water/oil interface occurred on their own within 40 min.

Micro-printed grid walls

To confine laterally the active nematic to channels, as shown in Fig. 4f, we used millimetre-sized platforms in a photoresist encompassing the rectangular enclosures. Such grids were introduced in the open observation chamber from the top and placed at the water/oil interface, consequently trapping the active nematics in the rectangular channels⁴¹. Grids were 3D printed with a two-photon polymerisation printer (GT Photonic Professional, Nanoscribe) with a negative-tone photoresist (IP-S, Nanoscribe) and a ×25 objective. The grids were directly printed on silicon substrates without any preparation to avoid adhesion of the resist to the substrate. After developing for 30 min in propylene glycol monomethyl ether acetate (99.5%, 484431, Sigma) and for 5 min in isopropanol, batch polymerisation occurred under UV exposure (5 min at 80% of light power). The pattern resolution achieved was about 50 nm. The grid thickness was 100 μm, to ensure a good resistance during manipulation.

Imaging and image processing

Images of the active nematic layer were acquired with a microscope (Eclipse Ti-E Inverted Microscope, Nikon) equipped with a confocal spinning disc (CSU-X1, Yokogawa), a motorised stage (Ti-S-EJOY, Nikon) and a ×10 objective (Nikon). The sample was excited with a laser beam at 647 nm with an exposure between 200 and 500 ms depending on the sample fluorescence. Images were captured with a camera (Orca Flash4.0, Hamamatsu) and acquired with the software NiS-Elements. The acquisition rate was 2 frames per second.

Image processing, including background correction, was carried out with the software ImageJ. The nematic tensor ${Q}\left(r,t\right)$ was computed from the images using custom Matlab scripts²³ that infer the local alignment of the microtubules using coherence-enhanced diffusion filtering. First, noise in the image was filtered out with a Gaussian blur of standard deviation σ₁. The pixel-level orientation was obtained by finding the direction along which the fluorescence intensity was most homogeneous and smoothed with a Gaussian blur of standard deviation σ₂. Finally, the nematic tensor Q was constructed by ensemble-averaging the molecular orientation tensor over a small circle of size β around each pixel. The three parameters σ₁, σ₂ and β were manually adjusted by visual inspection of the resulting director field. Velocity fields ${{\mathbf{u}}}\left(r,t\right)$ were calculated with the optical flow method detailed in ref. ⁶⁰ and associated Matlab codes, using the ‘classic+nl-fastp’ method.

The high-resolution images exhibit pixel-level noise, which hinders the calculation of the gradients of the fields, which are required to identify the defects (equation (7)) and viscometric surfaces (equation (10)). Therefore, we generated a coarse-grained field by sampling the field over regular steps (step scale ℓ_s). The same resolution was used for both the velocity and orientation fields. We tested the ideal resolution using the defect tracker (section ‘Analysis’) and chose a value of 16 pixels, which identifies the most number of defects correctly (while avoiding overestimating). One pixel equates to 0.65 μm, and so the characteristic active length scale corresponds to ℓ_ζ = 174 μm = 113 pixels = 7.07ℓ_s. Each experimental data point in Fig. 1c is separated by ℓ_s.

Simulations

Our active nematic simulations employ a hybrid lattice Boltzmann approach⁶¹ to reproduce the continuum nematohydrodynamics model⁶². The dynamics of the orientational order parameter ${Q}\left(r,t\right)=S\left(n\otimes n-{{\delta }}/3\right)$ at each position r and time t for a 3D identity matrix δ is described by the Beris–Edwards transport equation

$${{{{\mathcal{D}}}}}_{t}{Q}={{M }}{H},$$

(2)

where the right-hand side is the relaxation to equilibrium through a relaxation parameter M. The molecular field, ${H}=-\left(\frac{\delta F}{\delta {Q}}-\frac{1}{d}{\delta}\ {\mathrm{tr}}\left[\frac{\delta F}{\delta {Q}}\right]\right)$, corresponds to the nematic free energy F, where d is the dimensionality and ${\mathrm{tr}}\left[ \ \right]$ is the trace. On the left-hand side, ${{{{\mathcal{D}}}}}_{t}{Q}=\left({D}_{t}-R\right){Q}$ is a covariant derivative that accounts for material advection as ${D}_{t}={\partial }_{t}+{{\mathbf{u}}}\cdot {\nabla }$, which couples directly to the velocity field, and a corotational operator $R \ {Q} =\lambda {\left\{{E},\tilde{Q}\right\}}_{+}+{\left\{{\Omega},{Q}\right\}}_{-}-2\lambda \left({Q}:{L}\right)\tilde{Q}$. The corotational term couples the orientation to the velocity gradient ${L}=\nabla\otimes{{\mathbf{u}}}$ through the vorticity ${\varOmega}=\left({L}-{L}^{T}\right)/2$ and strain-rate ${E}=\left({L}+{L}^{T}\right)/2$ tensors, written using an (anti)commutator ${\left\{{A},{B}\right\}}_{\pm }={A}\cdot {B}\pm {B}\cdot {A}$, with a flow-aligning parameter λ and $\tilde{Q}\equiv {Q}+{\delta}/d$. The Beris–Edwards equation (equation (2)) is numerically solved by finite difference.

The velocity ${{\mathbf{u}}}\left({r},t\right)$ evolves according to the generalised Navier–Stokes equations

$$\rho {D}_{t}{{\mathbf{u}}}={\nabla }\cdot {\varPi}-\xi \cdot {{\mathbf{u}}},$$

(3)

with density ρ and friction tensor ξ. The stress Π consists of a viscous term 2ηE with viscosity η, a pressure term −pδ, an elastic term $K\left[2\lambda \left({Q}:{H}\right)\tilde{Q}-\lambda {\left\{{H},\tilde{Q}\right\}}_{+}+{\left\{{Q},{H}\,\right\}}_{-}-{\nabla }\left({Q}:\frac{\delta F}{\delta {\nabla }{Q}}\right)\right]$ and, most relevantly, an active term

$${\varPi}_{\zeta}=-\zeta{Q}.$$

(4)

Both the elastic and active terms couple the velocity field to the nematic field, but the active stress is directly proportional to the nematic field, with an activity coefficient ζ that leads to a bend instability when ζ > 0 (or a splay instability when ζ < 0), which drives deformation, wall formation and defect unbinding, leading to the active defect turbulence. The lattice Boltzmann algorithm simulates equation (3) and achieves near incompressibility ${\nabla }\cdot {{\mathbf{u}}}\approx 0$.The free energy includes a bulk component and a surface anchoring term F = ∫_Vf dV + ∫_Af_A dA. The bulk free energy density is constructed as a Landau–de Gennes expansion with a one-constant elastic Oseen–Frank term

$$f={A}_{0}\left[\left(\frac{1-\gamma /3}{2}\right){Q}:{Q}-\frac{\gamma }{3}{Q}:\left({Q}\cdot {Q}\right)+\frac{\gamma }{4}{\left({Q}:{Q}\right)}^{2}\right]+\frac{K}{2}\left({\nabla }\otimes {Q}\right)\vdots \left({\nabla }\otimes {Q}\right),$$

(5)

with γ controlling the distance from the isotropic–nematic phase transition and K the isotropic elastic constant. The surface free energy density is

$${f}_\mathrm{A}={W}_{1}\left({Q}-{Q}^{\perp }\right):\left({Q}-{Q}^{\perp }\right)+{W}_{2}\left({Q}:{Q}-{S}_{\rm{eq}}^{2}\right),$$

(6)

where W_1,2 are anchoring energies, ${S}_{{{{\rm{eq}}}}} = \left[ 1+3\sqrt{1-8/3\gamma } \right] /6$ is the equilibrium scalar order parameter and ${Q}^{\perp }={P}\cdot \left({Q}+{S}_{{{{\rm{eq}}}}}{\delta}/3\right)\cdot{P}$ for the surface normal projection operator P.

Except where otherwise stated, our 2D extensile nematic simulations used the following parameter values (in lattice Boltzmann units): density ρ = 1, rotational diffusivity M = 0.3375, flow-aligning parameter λ = 1, bulk energy density scale A₀ = 1, distance from the isotropic–nematic transition γ = 3, dynamic viscosity η = 4/3, Frank elasticity K = 0.05, friction ξ = 0 and extensile activity ζ = 0.1. Periodic boundary conditions were used in a system of 80 × 80 cells. The velocity and director fields were randomly initialised. A warmup time of T_W = 1 × 10⁴ was used before data were collected for T = 2 × 10⁴ lattice Boltzmann time steps.

Figure 4 shows that the conclusions arrived at for 2D extensile active turbulence hold under other conditions. As far as possible, we kept our simulation parameters unchanged from the extensile case and made only a few substitutions.

• Flow tumbling (Fig. 4a and Supplementary Video 5): substitute λ = 0.3. In Extended Data Fig. 7b, both λ = 0.3 and 0.6 are presented.

• Contractile (Fig. 4b and Supplementary Video 6): substitute ζ = −0.1 and system size 160 × 160. We note that these contractile simulations permit a small non-zero component to the out-of-plane director and velocity field. This escape into the third dimension is negligible everywhere except for a small region at the top of Supplementary Video 6, which persisted in time but did not grow.

• Isotropic friction (Extended Data Fig. 8): we substituted ξ = ξδ for lower friction ξ = 0.009 and higher ξ = 0.015. Other bulk parameters are given in ref. ³⁵.

• Anisotropic friction (Fig. 4c and Supplementary Video 7): we substituted $\xi =\left[\left[0.015,0\right],\left[0,0\right]\right]$.

• Quenched passive nematic (Extended Data Fig. 9 and Supplementary Video 10): the simulation parameters are ρ = 40, M = 0.3375, λ = 1, A₀ = 1, γ = 3, η = 40/6, K = 0.5, ξ = 0 and ζ = 0. It is initialised from the isotropic state.

• 2D channel confinement (Fig. 4d,e and Supplementary Video 8): periodic boundary conditions kept at the ends of the channels but the channel walls are impermeable, no-slip boundaries with anchoring energies W₁ = W₂ = 0.3. System dimensions are 130 × 25.

• 3D channel confinement (Fig. 4g and Supplementary Video 12): same as the 2D channel wall but now in a 3D square duct.

• Extended Data Fig. 2: we substitute density ρ = 40, rotational diffusivity M = 0.05, dynamic viscosity η = 1/6, activity ζ = 0.05, system size 256 × 256, warmup time T_W = 5 × 10² and data collection time T = 1.95 × 10⁴ lattice Boltzmann time steps.

Analysis

Defect analysis

Topological disclinations in both experiments and 2D simulations were identified by calculating the topological charge density^63,64,65

$$q=\frac{1}{4\pi }({\partial }_{x}{Q}_{x\alpha }{\partial }_{y}{Q}_{y\alpha }-{\partial }_{x}{Q}_{y\alpha }{\partial }_{y}{Q}_{x\alpha }),$$

(7)

using the summation convention on Greek indices. Points where q is greater or less than ±q_cut standard deviations are identified as k = ±1/2 defects. For the experiments, q_cut = 1.5, whereas for the simulations, q_cut = 4. Once each 2D defect was identified, its orientation was found through the angle

$$\psi =\frac{k}{k-1}\arctan \left(\frac{{\langle {{{\mathrm{sgn}}}}\left[k\right]{\partial }_{x}{Q}_{xy}-{\partial }_{y}{Q}_{xx}\rangle }_{\circ }}{{\langle {\partial }_{x}{Q}_{xx}+{{{\mathrm{sgn}}}}\left[k\right]{\partial }_{y}{Q}_{xy}\rangle }_{\circ }}\right),$$

(8)

with 〈⋅〉_∘ denoting averaging over a closed loop around the disclination⁶⁶. In 3D, defect lines were identified and characterised using the disclination density tensor⁶³ D constructed from gradients in the nematic Q tensor. In index notation, D_ij = ϵ_iμνϵ_jlk∂_lQ_μα∂_kQ_να. The tensor was interpreted as ${D}=s{{{\mathbf{R}}}}\otimes {{\mathbf{T}}}$, in terms of a non-negative scalar field s, the rotation vector ${{{{{{\mathbf{R}}}}}}}$ and tangent vector ${{\mathbf{T}}}$ along the disclination. The values of s approached a maximum at defect cores. We identified the defect lines as isosurfaces where s = 0.1. We characterised the local geometry of the disclination line through the angle between the rotation and tangent vectors $\cos \beta ={{{{{{\mathbf{R}}}}}}}\cdot {{\mathbf{T}}}$, where β is known as the twist angle. Values of $\cos \beta$ smoothly transitioned between −1 for −1/2 wedge profiles, through to +1 for +1/2 wedge profiles. Visualisations in 3D used the Mayavi Python library⁶⁷.

${{{\mathcal{Q}}}}$ criterion

We characterised the principal behaviour of flow fields by the ${{{\mathcal{Q}}}}$ criterion, which is defined to be the second invariant of the velocity gradient ${L}={\nabla }\otimes {{\mathbf{u}}}$ (ref. ⁶⁸)

$${{{\mathcal{Q}}}}=\frac{1}{2}\left({\left(\mathrm{tr}\left[{L}\right]\right)}^{2}-\mathrm{tr}\left[{L}^{2}\right]\right).$$

(9)

In the incompressible limit, $\mathrm{tr}\left[{L}\right]={\nabla }\cdot {{\mathbf{u}}}=0$, and so this definition reduces to equation (1), which we repeat here for convenience

$${{{\mathcal{Q}}}}=\frac{1}{2}\left(\|{\varOmega}\|^{2}-\|{E}\|^{2}\right),$$

(10)

where the squared norms are ∥A∥² = A_ijA_ij. ${{{\mathcal{Q}}}}\left({{\mathbf{r}}},t\right)$ is shown in Supplementary Video 13, and the isosurfaces of ${{{\mathcal{Q}}}}=0$ were identified using the skimage Python library⁶⁹.

If ${{{\mathcal{Q}}}} > 0$, vorticity dominates over strain rate, whereas if ${{{\mathcal{Q}}}} < 0$, the strain rate dominates. Where ${{{\mathcal{Q}}}}=0$, the magnitudes of the vorticity and the strain rate are equal. In 2D, the isolines of ${{{\mathcal{Q}}}}=0$ must form closed loops, and in 3D, ${{{\mathcal{Q}}}}=0$ contours must form closed isosurfaces enclosing vorticity-dominated regions. There are only two invariants of L in 2D, and the first $\mathrm{tr}\left[{L}\right]={\nabla }\cdot{{\mathbf{u}}}=0$ is due to incompressibility. Therefore, if ${{{\mathcal{Q}}}}=0$, all the invariants of L are zero, which indicates that all the eigenvalues are zero. This in turn means the velocity gradient tensor is singular and nilpotent. Simple shear flow is an example, as is any viscometric flow in which streamlines are equi-distance apart because there is no stretching or elongation of the fluid^70,71. Thus, we refer to ${{{\mathcal{Q}}}}=0$ contours as viscometric surfaces.

The tail of finite probabilities to observe non-zero separation distances (d > 0.1ℓ_ζ) in simulations seen in Fig. 1c is due to the rapid shrinking of ${{{\mathcal{Q}}}} > 0$ regions around defects during pair-annihilation events, leading to rare instances of false positives when viscometric surfaces have vanished one frame before the defect tracker (section ‘Defect analysis’) has identified that annihilation has occurred. A single outlier is identified from the simulation dataset that is not associated with pair annihilation. In this sole, ephemeral instance, we observed two +1/2 defects in close proximity with one of the two inside the ${{{\mathcal{Q}}}} > 0$ region. This configuration is rare due to its high free energy cost and is an outlier that was removed from our statistics. It is reminiscent of the impermanent +1 complexes in contractile nematics (Fig. 4b), though much less likely and with a different relative defect orientation.

Comparing zero-isosurfaces ${{{\mathcal{Q}}}}$ with vorticity

Throughout this work, we employ the zero-isolines of the ${{{\mathcal{Q}}}}$ criterion to identify viscometric surfaces as the boundaries between flow structures. Under incompressibility, the magnitude of the symmetric and antisymmetric velocity gradients balance when ${{{\mathcal{Q}}}}=0$ to give a finite simple shear. However, it is also a possibility that the velocity gradients in the flow completely vanish. To compare these two possibilities for the ${{{\mathcal{Q}}}}$ criterion, we explore contours where contributions from Ω go to zero. In any 2D coordinate basis, Ω has only off-diagonal components Ω₂₁ = −Ω₁₂ = ω in terms of the vorticity pseudovector $\mathbf{\upomega }$. Hence, locations where the rotation-rate tensor vanishes can be simply obtained from a sign change in ω. Obtaining contours where the strain rate vanishes is less direct since the tensorial components vary with coordinate basis, as there is no clear handedness to this object and no pseudovector can be constructed in 2D. At locations where the vorticity zero-lines and ${{{\mathcal{Q}}}}$-criterion zero-lines coincide, the strain-rate contours must be zero due to the incompressibility. Otherwise, these viscometric lines are where there is a finite shear from the balance between vorticity and strain rate.

Distribution of vortex characteristics

Since viscometric surfaces form the boundary encircling vortex-dominated domains from strain-rate-dominated regions, we quantify the distribution of fluid elements composing each vortex domain (where ${{{\mathcal{Q}}}} > 0$). After identifying the list of points defining the ${{{\mathcal{Q}}}}=0$ boundary, vortices are identified as the enclosed regions where ${{{\mathcal{Q}}}} > 0$. A clustering algorithm identifies the constituent vortex points. Vortex area distributions are found as the total number of lattice Boltzmann nodes or experimental pixels identified inside a viscometric surface with ${{{\mathcal{Q}}}} > 0$. We calculate the square of the relative shape anisotropy κ of each vortex, written in terms of the first (I₁) and second (I₂) invariants of the moment of inertia tensor⁷² in d dimensions as

$${\kappa }^{2}=1-\frac{2d}{d-1}\frac{{I}_{2}}{{I}_{1}^{2}}.$$

(11)

The enclosed circulation is defined as ${{\varGamma }}={\oint }_{c}{{\mathbf{u}}}\cdot\mathrm{d}{{\mathbf{l}}}=\oint \boldsymbol{\omega }\cdot\mathrm{d}{{\mathbf{S}}}$. We apply the second definition to simplify the handling of non-zero genus vortices. The circulation distribution in Fig. 1 is non-dimensionalised to compare the experimental and simulated distributions by dividing by ${{{\varGamma }}}_{0}={\omega }_{0}{\ell }_{\zeta }^{2}$. The vorticity scale ω₀ was identified as the standard deviation of the vorticity distribution. We calculate the active length scale as

$${\ell }_{\zeta }={\sigma }^{-1/2},$$

(12)

where the defect number density $\sigma =\left({N}_{+1/2}+{N}_{-1/2}\right)/\left(T{L}^{2}\right)$ for N_±1/2 nematic defects, total time steps T and system size L.

Splay-bend parameter

The splay-bend parameter^40,73

$${S}_{{{{\rm{SB}}}}}={\partial }_{i}{\partial }_{j}{Q}_{ij}$$

(13)

is used to visualise bend walls as line-like structures with large negative values⁴⁰. To interpret S_SB, consider a uniaxial 2D nematic with constant scalar order S. Under these conditions ${S}_{{{{\rm{SB}}}}}=S{\nabla }\cdot \left[{{\mathbf{n}}}\left({\nabla }\cdot {{\mathbf{n}}}\right)-{{\mathbf{n}}}\times \left({\nabla }\times {{\mathbf{n}}}\right)\right]$. The first term inside the divergence is the splay and the second term is the bend, leading to the interpretation that S_SB represents the difference between the divergence of the splay and the bend. Because the active force density is the divergence of the active stress (equation (4))

$$f_{\zeta }=-\zeta\, {\nabla }\cdot {Q},$$

(14)

then in active nematics the splay-bend parameter can be understood to be proportional to the divergence of the active force

$${S}_{\rm{SB}} \propto {\nabla }\cdot f_{\zeta }.$$

(15)

Defects and viscometric surfaces

To find the probability distribution of nearest distances between defects and viscometric surfaces (${{{\mathcal{Q}}}}=0$ contours), we calculate the distances for all defects to each point on the boundary and included only the smallest distance (to avoid introducing cutoff distances). For mirror-symmetric configurations (Fig. 2c), only the nearest boundary is counted.

To calculate the distribution of the alignment angles shown in Fig. 2g, we first group +1/2 defects to ${{{\mathcal{Q}}}}=0$ contours. Each defect is associated with a boundary if the defect resides within two simulation or experimental sites away from any point of the boundary (experimental sites use the resolution details explained in section ‘Imaging and image processing’). The closest point j between the defect and the list of points on the ${{{\mathcal{Q}}}}=0$ boundary is found and is the reference point when calculating the tangent vector. The tangent vector is then calculated using a forward derivative with the next point in the boundary list j + 1 (with the forward direction matching the +1/2 defect’s orientation) as

$${{\mathbf{t}}}=\frac{{{\mathbf{r}}}(\;j+1)-{{\mathbf{r}}}(\;j)}{\left\vert {{\mathbf{r}}}(\;j+1)-{{\mathbf{r}}}(\;j)\right\vert },$$

(16)

where ${{\mathbf{r}}}(\;j)$ is the position vector of the chosen point j on the ${{{\mathcal{Q}}}}=0$ boundary. We chose the forward derivative over a centred derivative because the flow structure ahead of the defect is more consequential to the future dynamics of the defect trajectory. The +1/2 defect orientation vector is found with equation (8). Each alignment angle is, therefore, found from the angle between these two vectors and presented in the angle interval from 0° to 90°. If the defect is associated to the mirror-symmetric ${{{\mathcal{Q}}}}=0$ regime, then the same +1/2 defect orientation vector is included for the alignment angle calculation with both boundaries.

To investigate the mirror-symmetry breaking, we sort the configurations based on the three classes of defect and flow configurations (Fig. 2c–e). For each +1/2 defect, we calculate ${\left\langle {{{\mathcal{Q}}}}\right\rangle }_{{{\Delta }}{r}^{2}}$ as the average ${{{\mathcal{Q}}}}$ criterion in a small region Δr² set to be a rectangle of seven by six lattice units on either side of the mirror-symmetry axis of the defect director field (the defect tail). From ${\left\langle {{{\mathcal{Q}}}}\right\rangle }_{{{\Delta }}{r}^{2}}$, three different defect populations can be identified: one group where ${\left\langle {{{\mathcal{Q}}}}\right\rangle }_{{{\Delta }}{r}^{2}}$ is close to zero (with mirror symmetry), and two where ${\left\langle {{{\mathcal{Q}}}}\right\rangle }_{{{\Delta }}{r}^{2}}$ has a large positive or negative value (the broken-mirror-symmetry cases). To ensemble-average over these three regimes, defects are binned into lowest 10% of ${\left\langle {{{\mathcal{Q}}}}\right\rangle }_{{{\Delta }}{r}^{2}}$, middle 80% and highest 10%. This gives Extended Data Fig. 2b, Extended Data Fig. 2a and Extended Data Fig. 2c, respectively. The results are when varying the exact binned regions Δr². Extended Data Fig. 2a shows the ensemble-averaged case of mirror-symmetric defects at the ${{{\mathcal{Q}}}}=0$ intersection, with opposite-handed vortices on either side. Extended Data Fig. 2b shows the broken-mirror-symmetry state for defects with a clockwise-handed ${{{\mathcal{Q}}}} > 0$ vortex to the right of the defect head and ${{{\mathcal{Q}}}} < 0$ to the left and vice versa in Extended Data Fig. 2c. In both cases, the defect aligns parallel with the ${{{\mathcal{Q}}}}=0$ tangent. In addition, the local velocity field in Extended Data Fig. 2b,c on either side of the defect has the same curvature direction as the vortex handedness, whereas the mirror-symmetric regime has an inversion to the focal point.

Defect trajectories

To investigate the relationship between +1/2 defect trajectories and the configuration with viscometric surfaces, we resolve the individual trajectories in active turbulence. We iteratively build the trajectory for each defect at time t by identifying candidate defect positions in the next time step (t + 1). Candidate t + 1 defects are filtered to keep only those that are separated by less than eight lattice cells and are oriented in front of the defect. The t + 1 defect in the trajectory is chosen such that it maximises the cosine of the relative orientation $\cos ({\psi }_{t}-{\psi }_{t+1})$. Trajectories are removed from the statistics if there are three or fewer resolved points. All trajectories with nine or more recorded points are shown in Extended Data Fig. 5a, along with the corresponding viscometric surface state. The trajectories are classified as being in the mirror-symmetric state if there are two viscometric contours within a distance of 0.1ℓ_ζ of the defect position, otherwise they are handed. Extended Data Fig. 5b shows the curvature of the trajectory multiplied by the handedness. The trajectory curvature is calculated as the derivative of the trajectory tangent vector by the arc length and then multiplied by the handedness of the defect trajectory (−1 for anticlockwise and +1 for clockwise). The scatter plot shows the defect velocity. The mean +1/2 defect velocity was found from the distance between separated points in the trajectory divided by the time interval. This mean velocity is non-dimensionalised by the most probable speed of the overall velocity field u₀ (found from the peak of the velocity distribution).

Modelling

Stokesian solitary-defect model

The ${{{\mathcal{Q}}}}$ criterion and flow field around +1/2 and −1/2 topological defects is shown in Fig. 2b,f. The ${{{\mathcal{Q}}}}$-criterion field is determined from the velocity field solutions ${{{\mathbf{u}}}}_{\pm }$ for a single solitary ±1/2 defect, as first derived by Giomi et al.²⁸. To find the ideal flow-field structure around solitary defects of topological charge k, those authors fixed the director field ${\mathbf{n}}_{k}=\cos \left(k\phi \right)\hat{x}+\sin \left(k\phi \right)\hat{y}$, and so the Beris–Edwards equation (equation (2)) does not evolve. They then solved the generalised Navier–Stokes equations (equation (3)) for the steady state (${D}_{t}{{\mathbf{u}}}=0$) in the absence of friction and with negligible elastic stresses, leaving the Stokes equation for the velocity field,

$$\eta {\nabla }^{2}{{\mathbf{u}}}-{\nabla }p+{\mathbf{f}}_{\zeta }=0,$$

(17)

as a response to the active force density ${\mathbf{f}}_{\zeta }$ (equation (14)). For an extensile +1/2 defect (k = +1/2), the active force ${\mathbf{f}}_{\zeta }=-\zeta \hat{x}/2r$ is in the direction of the defect $-\hat{x}$ (bend side) and decays inversely with distance r from the defect core²⁸. This rapid decay of the force is the basis for the simple view of defects as point sources of forcing. Although a bulk active nematic cannot exert a global net force, the conceit of this ideal Stokesian model is that a single solitary defect breaks the topological charge neutrality to give a net force. The solution to equation (17) can be written as

$${{\mathbf{u}}}\left({{\mathbf{r}}}\right)=\int\,\mathrm{d}{A}^{{\prime}}\,{G}\left({{\mathbf{r}}},{{{\mathbf{r}}}}^{{\prime} }\right)\cdot f_{\zeta }\left({{{\mathbf{r}}}}^{{\prime} }\right)$$

(18)

with the 2D Oseen tensor²⁸

$${G}\left({{\mathbf{r}}},{{{\mathbf{r}}}}^{{\prime} }\right)=\frac{1}{4\pi \eta }\left[\left(\log \frac{L}{\left\vert {{\mathbf{r}}}-{{{\mathbf{r}}}}^{{\prime} }\right\vert }-1\right){{\delta }}+\frac{({{\mathbf{r}}}-{{{\mathbf{r}}}}^{{\prime} })\otimes (\boldsymbol{r}-{{{\mathbf{r}}}}^{{\prime} })}{{\left\vert {{\mathbf{r}}}-{{{\mathbf{r}}}}^{{\prime} }\right\vert }^{2}}\right],$$

(19)

in a system bound by the length scale L. Substituting in the active force for the fixed, solitary defects gives the velocity fields around solitary +1/2 and −1/2 defects to, respectively, be

$${{{\mathbf{u}}}}_{+}(r,\phi )=-\frac{\zeta }{12\eta }\left[\left\{3(R-r)+r\cos 2\phi \right\}\hat{x}+r\sin 2\phi \hat{y}\right],$$

(20)

$$\begin{array}{l}{{{\mathbf{u}}}}_{-}(r,\phi )=-\frac{\zeta r}{12\eta R}\left[\left\{\frac{3}{4}(r-R)\cos 2\phi -\frac{R}{5}\cos 4\phi \right\}\hat{x}\right.\\\left.\qquad\qquad\qquad\quad -\left\{\left(\frac{3}{4}r-R\right)\sin 2\phi +\frac{R}{5}\sin 4\phi \right\}\hat{y}\right],\end{array}$$

(21)

where ζ is the activity, η is the viscosity and R is an integration length scale due to the logarithmic nature of hydrodynamic interactions in 2D (section ‘Stokesian line-force model of bend walls’). These are shown in Fig. 2b,f. Taking the derivatives of equations (20) and (21) produces the velocity gradient tensor ${L}={\nabla }\otimes {{\mathbf{u}}}$. The ${{{\mathcal{Q}}}}$-criterion field is then calculated as the second invariant of L. These calculations and corresponding plots were performed using Mathematica⁷⁴. For the +1/2 defect case, the ${{{\mathcal{Q}}}}$ criterion takes the form

$${{{{\mathcal{Q}}}}}_{+}=\left(\frac{\eta \zeta }{6}\right)^{2}\left(3\sin^{2}\phi -1\right).$$

(22)

In this construction, the +1/2 defect is aligned with a self-propulsion direction in the (negative) $\hat{x}$ direction, with an angle $\theta =\sin^{-1}\left({3}^{-1/2}\right)\approx 35.2{6}^{\circ }$ to the ${{{\mathcal{{Q}}}_{+}}}=0$ line. This angle is compared in Fig. 2g against the observed distribution of alignment angles in simulations and experiments as a benchmark for an isolated +1/2 defect. The solution for this angle is predicted independently of the activity, viscosity and overall system size.

Stokesian straight bend-wall model

Since our experimental and numerical results indicate that bend walls are coincident with ${{{\mathcal{Q}}}}=0$ and are crucial to the spontaneous self-constraint, we explore a series of models for the active flows generated by bend walls to identify which features of the bend walls are vital to this interdependence. Bend walls are known to arise from the hydrodynamic bend instability⁷⁵, leading to arch-like bends of the director field, reminiscent of Néel walls³⁰. First consider bend walls modelled as infinitely long, perfectly straight bands of alternating bend and splay given by ${\mathbf{n}} = \cos \theta \hat{x}+\sin \theta \hat{y}$, where the angle θ is

$$\theta (\,y;\lambda )=\pi\cos^{2}\left(\frac{y}{\lambda }\right),$$

(23)

for a modulation length scale λ. This generates the force density field ${\mathbf{f}}_{\zeta }=\zeta \frac{\pi }{\lambda }\sin \frac{2y}{\lambda }\left(\cos 2\theta \hat{x}+\sin 2\theta \hat{y}\right)$. Since the system has translational symmetry in x, only derivatives with respect to y exist for the pressure and velocity. Through the incompressibility equation $\nabla \cdot {{\mathbf{u}}}=0$, the absence of x gradients requires $\frac{\partial {{{u}}}_{y}}{\partial y}=0$, where ${\mathbf{u}} = u_x{\hat{x}} + u_y{\hat{y}}$. This leads to only one non-zero contribution to the velocity gradient tensor $\frac{\partial {{{u}}}_{x}}{\partial y}$, which is obtained by integrating the x momentum in equation (17). The velocity gradient tensor is

$${L}=-\zeta \frac{\sin \left(\pi \cos \left[2y/\lambda \right]\right)}{2\eta }\left(\begin{array}{ll}0&1\\ 0&0\end{array}\right).$$

(24)

As this is upper diagonal at all points (representing simple horizontal shear), it is a viscometric flow and ${{{\mathcal{Q}}}}=0$ everywhere. Thus, a straight, infinitely long series of kink walls is insufficient to explain the colocation of bend walls and ${{{\mathcal{Q}}}}=0$.

Wavy bend-wall model

Next, we consider whether the bend-wall curvature explains their coincidence with ${{{\mathcal{Q}}}}=0$. The bend walls from section ‘Stokesian straight bend-wall model’ are perturbed into infinitely long sinusoidal waves with the director field once again of the form ${\mathbf{n}}=\cos \theta \hat{x}+\sin \theta \hat{y}$, but where

$$\theta \left(x,y;\lambda \right)=\pi\cos^{2}\left(\frac{\pi x}{4\lambda }\right)+\frac{\pi y}{\lambda }.$$

(25)

This director field generates a periodic sequence of bend and splay walls that modulate sinusoidally about slices of $\hat{y}$ (Extended Data Fig. 3a). This initial director field is held fixed and the velocity field is numerically evolved to a steady state according to equation (3). This simple model of bend walls is sufficient to generate vortices enclosed by viscometric contours (Extended Data Fig. 3b). The vortices reside on the inside regions of the bend and splay walls with the greatest curvature, with alternating handedness generated through the coupling between the generated active force and the orientation of the wall curvature.

To further explore the nonlinear coupling between the modulated director field and the active flow field, we then hold the resulting initial steady-state velocity field fixed but allow the director field to evolve according to equation (2). The bend walls proceed to constrict towards a thin kink line, while the strong divergence in the splay wall breaks open, leaving minimised gradients in splay around the bend walls (Extended Data Fig. 3c). This demonstrates the active instability that drives growth in bend-type deformations. Even with an iterative progression of the two fields, the bend walls drive flows and the flows in turn concentrate and enhance the bend⁷⁵. Since the centre line of the bend walls coincides with ${{{\mathcal{Q}}}}=0$, the backbones themselves are largely undeformed, whereas the nearby nematic field is rotated towards a parallel alignment with the bend-wall centre line, localising the gradients in the bend. Iterating again demonstrates that the vortices begin to merge and elongate. The centre line of the bend wall still resides on ${{{\mathcal{Q}}}}=0$.

Overall, this model demonstrates that a modulation in the bend walls is able to split distinct ${{{\mathcal{Q}}}}$ regions without needing defects. The geometry of the flow generated by the bend has ${{{\mathcal{Q}}}}=0$ on the centre of the bend wall, which prevents a bend wall from deforming. The active flows can constrict but not cleave the bend walls. The shape of a bend wall can be perturbed only by the creation of defects.

Stokesian line-force model of bend walls

The hydrodynamic instability constricts an infinitely long bend into narrow kink walls, and their curvature facilitates closed ${{{\mathcal{Q}}}}=0$ contours (section ‘Analysis’). However, after the initial onset of active turbulence, finitely long bend walls continue to arise through constriction and are unzipped by +1/2 defects (Supplementary Video 4; refs. ^15,33). The active force density is non-negligible along the bend walls and so we propose a simplified model of finite narrow kink walls being unzipped by +1/2 defects modelled as an idealised line of active force. As before (section ‘Experiments’), elastic stresses are neglected and the Stokes equation (equation (17)) is solved for the velocity field and ${{{\mathcal{Q}}}}=0$ contours. This is done for three idealised bend-wall conformations: (1) a point, (2) a finite straight line and (3) a circular arc. For each case, the Stokes equation (equation (17)) is numerically solved on a 1,000 × 1,000 grid. The force lines for a finite straight line and a circular arc are constructed by arranging 500 point sources in a linear formation, with a constant forcing magnitude oriented parallel to the line tangent. Each point on the discretised line contributes to the overall velocity field through the Oseen tensor (equation (19)).

Point force

In the far-field limit away from a solitary bend wall, it is effectively a point force. From the Oseen tensor (equation (19)), crudely modelling a bend wall as a point force ${f}_{\zeta }\hat{x}$ at the origin produces a 2D Stokeslet:

$${{\mathbf{u}}}\left({{\mathbf{r}}}\right)=\frac{{f}_{\zeta }}{4\pi \eta }\left[\left(\log \frac{L}{\left\vert {{\mathbf{r}}}\right\vert }-1\right)\hat{x}+\frac{x{{\mathbf{r}}}}{{\left\vert {{\mathbf{r}}}\right\vert }^{2}}\right].$$

(26)

Taking the gradient results in the ${{{\mathcal{Q}}}}$ criterion

$${{{\mathcal{Q}}}}=-{\left(\frac{{f}_{\zeta }}{4\pi \eta \left\vert {{\mathbf{r}}}\right\vert }\right)}^{2}\cos 2\theta ,$$

(27)

which predicts an intersection of viscometric surfaces at an angle θ = 45°. A numerical solution for the single point is shown in Fig. 3c.

Finite straight line

In the vicinity of a finite straight-kink wall, the flow-field geometry differs from the point-source-like far-field approximation. A horizontal line of constant active force density is constructed using 500 point sources arranged across 500 horizontal lattice points, oriented towards the positive $\hat{x}$ direction. The velocity field and zero-isolines of the ${{{\mathcal{Q}}}}$ criterion (equation (1)) are shown in Fig. 3c. The ${{{\mathcal{Q}}}}$ criterion retains the mirror symmetry observed for the solitary defect or far-field point source, but now differs by constraining the alignment angle θ towards more acute values. Smaller defect alignment angles in the proximity of bend walls are more consistent with the peak in Fig. 2g, compared with the angle predicted by the solitary-defect model (section ‘Experiments’).

Circular arc

To provide an intuition of the flow geometry generated by bend walls with curvature, we next consider a circular arc force centred on the origin. The arc is parameterised in terms of s so that it can wrap out an angle in a prescribed interval with end points lying between 0 and 2π. Positions on the arc are ${{{\mathbf{r}}}}^{{\prime} }(s)=R\left(\cos s\hat{x}+\sin s\hat{y}\right)$, where R is the radius. As before, the force contour is assumed to have constant magnitude f_ζ and orient azimuthally. By choosing the forces to follow the arc in a clockwise sense, the force is ${\mathbf{f}}_{\zeta }^{\,{\prime} }(s)={f}_{\zeta }\left(\sin s\hat{x}-\cos s\hat{y}\,\right)$. Numerical integration is performed using 500 point sources distributed between s = 5π/8 and 3π/8. The results for the velocity field and ${{{\mathcal{Q}}}}$ criterion are shown in Fig. 3e. The ${{{\mathcal{Q}}}}$ criterion goes to zero when $\left\vert {{\mathbf{r}}}\right\vert =R$. This result shows that a simple force model can capture the correlation between elongated nematic deformation and ${{{\mathcal{Q}}}}=0$. Through a comparison with the finite straight line case, we can see that curvature facilitates the transformation from two vortices to one at the source of the active forcing. Therefore, lines of active force generated by narrow, bend walls can capture the essential geometry of the flow field if they are (1) finite and (2) curved.

Reporting summary

Further information on the research design is available in the Nature Portfolio Reporting Summary linked to this article.