Inverse design of high-dimensional quantum optical circuits in a complex medium

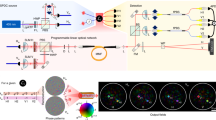
Abstract

Programmable optical circuits are an important tool in developing quantum technologies such as transceivers for quantum communication and integrated photonic chips for quantum information processing. Maintaining precise control over every individual component becomes challenging at large scales, leading to a reduction in the quality of operations performed. In parallel, minor imperfections in circuit fabrication are amplified in this regime, dramatically inhibiting their performance. Here we use inverse design techniques to embed optical circuits in the higher-dimensional space of a large, ambient mode mixer such as a commercial multimode fibre. This approach allows us to forgo control over each individual circuit element, and retain a high degree of programmability. We use our circuits as quantum gates to manipulate high-dimensional spatial-mode entanglement in up to seven dimensions. Their programmability allows us to turn a multimode fibre into a generalized multioutcome measurement device, allowing us to both transport and certify entanglement within the transmission channel. With the support of numerical simulations, we show that our method is a scalable approach to obtaining high circuit fidelity with a low circuit depth by harnessing the resource of a high-dimensional mode mixer.

Main

A programmable optical circuit is an essential element for applications in fields as diverse as sensing, communication, neuromorphic computing, artificial intelligence and quantum information processing^1,2,3. The production of large, reprogrammable circuits is of paramount importance for coherently processing information encoded in light. However, there remain many challenges associated with the design, manufacture and control of such circuits, which normally require a sophisticated mesh of interferometers constructed with bulk or integrated optics^2,4. The conventional construction of these circuits exploits universal programmability on two-dimensional unitary spaces to construct arbitrary high-dimensional unitary transformations^5,6,7,8, referred to as the ‘bottom-up’ technique here (Fig. 1a). Over the past two decades, the technological development of integrated programmable circuits has enabled universal programmability in up to 20 path-encoded modes, containing a few hundreds of optical components on the same chip^9,10,11,12.

Fig. 1: Design of programmable optical circuits.

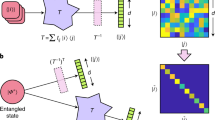
a–c, A general linear transformation ${\mathbb{T}}$ can be implemented via the conventional bottom-up approach (a), where the circuit is constructed from units consisting of beamsplitters (BS) and phase shifters (P), or the proposed ‘top-down’ approach (b), where a target d-dimensional linear circuit is embedded within a large ambient mode mixer with dimension n > d, where n − d auxiliary modes serve as an additional resource. This technique harnesses random unitaries U_j (such as a complex scattering system) interspersed with controllable phase planes P_j implemented via SLMs, which provide programmability over the target circuit. c, A similar approach using multiplane light converters, where the random unitaries are replaced with free-space propagation F.

Imperfections in optical circuits such as scattering loss, unbalanced mode mixing and undesired crosstalk between modes are problematic as they reduce the accuracy and success probability of the implemented circuit^{13,14,15,16,17}. These issues become increasingly challenging in large dimensions, as the number of optical elements grows quadratically with the size of the circuit^2,4. Such imperfections can be addressed—to some extent—by increasing the depth of the circuit through the introduction of additional phase shifters and beamsplitters^{13,14,15,18,19}. However, these additional components necessitate additional control, further increasing the demands associated with circuit complexity.

In this work, we present an alternative solution where the optical circuit is embedded in a higher-dimensional space of a large ambient mode mixer such as a random scattering medium, placed between reprogrammable phase planes (Fig. 1b). This top-down approach harnesses the complicated scattering process within a large mode mixer to forgo control over each individual circuit element. Instead, an inverse design approach is used, which employs algorithmic techniques to program an optical circuit with a desired functionality within the random scattering medium^20,21. Similar approaches based on inverse design have been used in multiplane light converters for spatial-mode manipulation^22,23,24, where free-space propagation is commonly used in place of a random scattering medium (Fig. 1c). Furthermore, inverse design techniques have also enabled a variety of optical circuits tailored towards specific functionalities, ranging from designs of on-chip photonic devices²⁵ to arrangements of bulk optical elements for fundamental quantum experiments^26,27,28,29.

The capability to manipulate quantum states of light using large-scale programmable circuits promises a myriad of applications in quantum information science, ranging from the demonstration of computational advantage³⁰ to the realization of quantum networks³¹. In this regard, high-dimensional quantum systems offer important advantages in terms of increasing information capacity and noise resistance in quantum communication^32,33,34, reducing multiqubit circuit complexity³⁵ and enabling more practical tests of quantum non-locality^36,37. Although methods for the transport^38,39 and certification^40,41,42 of high-dimensional entanglement have seen rapid progress over the past few years, scalable techniques for its precise manipulation and measurement are still lacking. As an alternative to the bottom-up approach normally implemented on integrated platforms¹⁰, inverse design techniques have been used for realizing quantum gates in dimensions up to d = 4 using bulk optical interferometers^43,44 and d = 5 with multiplane light conversion^45,46. In parallel, recent advances in control over light scattering in complex media^47,48 have enabled linear optical circuits for classical light^49,50 and demonstrations of programmable two-photon quantum interference^51,52,53, showing their clear potential to serve as a high-dimensional quantum photonics platform.

In this Article, we harness light scattering through an off-the-shelf multimode fibre (MMF) to program generalized quantum circuits for transverse spatial photonic modes in dimensions up to seven. We apply these circuits for the manipulation of high-dimensional entangled states of light in multiple spatial-mode bases, demonstrating high-dimensional Pauli ${\mathbb{Z}}$ and Pauli ${\mathbb{X}}$ gates, discrete Fourier transforms and random unitaries in the macro-pixel and orbital angular momentum spatial-mode bases^42,54. Furthermore, in contrast to single-outcome projective measurements that are inherently inefficient⁵⁵, our technique realizes generalized transformations to a spatially localized ‘pixel’ basis, effectively turning the channel itself into a generalized multioutcome measurement device. By harnessing this functionality, we show how the on-demand programmability of our gates enables us to both transport and certify entanglement within the same complex medium. Such multioutcome measurements can be easily integrated with next-generation single-photon-detector arrays⁵⁶ and provide a key functionality in many quantum information applications, such as allowing one to overcome fair-sampling assumptions⁵⁷.

Top-down programmable circuits

An optical circuit is described by a linear transformation ${\mathbb{T}}$ that maps a set of input optical modes onto a set of output modes^58,59. The linear circuit ${\mathbb{T}}$ of dimension d is built from a cascade of optical mode mixers U and phase shifters P. A deterministic construction can be based on a cascade of reconfigurable Mach–Zehnder interferometers, where U_j represents the embedded balanced two-mode mixer, that is, a 50:50 beamsplitter, and P_j denote phase shifters (Fig. 1a)^5,7. As an alternative to this deterministic bottom-up construction, the top-down design presented here relies on the capability to harness large, complex, intermodal mode mixers U_j of dimension n $({U}_{j}\in {{{\mathcal{U}}}}({{{\bf{n}}}}))$ and reconfigurable phase planes P_j = diag(e^iθ) to construct a programmable target circuit ${\mathbb{T}}$ of a smaller size (d ⩽ n) embedded within the larger mode mixers (Fig. 1b). The decomposition of such a top-down programmable circuit is represented as

$${{{\bf{T}}}}\approx \mathop{\prod }\limits_{j = 1}^{L\leqslant {{{\mathcal{O}}}}({{{\bf{d}}}})}{U}_{j}{P}_{j},$$

(1)

where L is the depth of the circuit (number of layers) and the target circuit ${\mathbb{T}}$ is embedded in the total transfer matrix of the system, T. Optimal choices for the large mode-mixer dimension (n) and circuit depth (L) for a given target circuit dimension (d) are discussed in the ‘Programmability and scalability’ section.

We experimentally construct the programmable optical circuit with a two-metre-long graded-index MMF positioned between two programmable phase planes P₁ and P₂ implemented on spatial light modulators (SLMs) (Fig. 2a). The MMF serves as a large, complex mode mixer with dimension n ≈ 200 that provides complicated intermodal coupling^60,61,62, whereas the SLMs provide programmability over the circuit to be implemented. The circuit can be decomposed as T = U₂P₂U₁P₁, where U₁ represents the transfer matrix of the optical system consisting of the MMF and the associated coupling optics and U₂ is the 2f lens system. To construct the circuit, we begin by characterizing U₁ in a referenceless manner via our developed technique⁶³. Random phase patterns are displayed on the planes P₁ and P₂ and the resulting intensity speckle images are measured at the output. This dataset is then used to optimize the machine learning model that describes the optical system of our experiment using a gradient descent method, which takes ∼1 min to be calculated on a graphics processing unit. Once we have complete knowledge of the mode mixer U₁, a given target circuit is then programmed using a solution of phase patterns obtained from the wavefront-matching (WFM) algorithm^25,64,65. The WFM algorithm is an inverse design technique that calculates the reconfigurable phase planes by iterating through each of them to maximize the overlap between a set of input fields with the desired output ones, and repeating this procedure several times⁶³. The process of finding the optimal phase patterns takes a few seconds for a two-dimensional circuit to ∼1 min for a seven-dimensional circuit. Methods provides further details on transfer matrix acquisition or circuit construction.

Fig. 2: Experimental setup.

a, A high-dimensional spatially entangled two-photon state is generated via Type-II SPDC in a ppKTP crystal. The two photons are spatially separated by a polarizing beamsplitter (PBS) and sent to two parties, namely, Alice and Bob. Alice performs single-outcome projective measurements ${\hat{\Pi}}_{a}^{\mu}$ that measure whether a photon is carrying spatial mode a from modal basis μ. These are performed by a combination of an SLM (SLM₃), SMF and a single-photon avalanche photodiode (APD). Bob implements a top-down programmable circuit that is constructed from an MMF placed between two programmable SLMs (SLM_1,2). The circuit is used to program a variety of high-dimensional quantum gates and serves as a generalized multioutcome device. The circular inset shows a coincidence image depicting a five-outcome measurement in basis μ = 1 performed with the Fourier gate ${\mathbb{F}}$ at Bob. The image is obtained by scanning a detector across the output of the circuit, conditioned on the measurement of ${\hat{\Pi}}_{a = 0}^{\mu = 1}$ at Alice, and shows a large intensity in mode 0 due to strong spatial-mode correlations. Coincidence detection events between Alice and Bob are registered by time-tagging electronics. b, Charge-coupled device images demonstrating the operation of the Fourier gate ${\mathbb{F}}$ as a multioutcome measurement of classical macro-pixel modes prepared in basis μ = 1 in dimensions d = {2, 3, 5}. Note that although the input modes have the same amplitude for a given d, they are orthogonal in phase (not seen in the intensity images). L, lens; F, filter; HWP, half-wave plate.

Using the WFM algorithm, we implement a variety of different target circuits ${\mathbb{T}}$ on our system including the identity ${\mathbb{I}}$, high-dimensional analogues of Pauli ${\mathbb{Z}}$ and Pauli ${\mathbb{X}}$, Fourier ${\mathbb{F}}$ and random unitaries ${\mathbb{R}}$ in dimensions d = {2, 3, 5, 7} for two different input transverse spatial-mode bases (macro-pixel⁴² and orbital angular momentum⁵⁴). Our circuits perform generalized basis transformations to a localized output ‘pixel’ basis with a maximum theoretical efficiency of unity (see the ‘Programmability and scalability’ section), enabling multioutcome measurements in any given basis. The target output modes are randomly selected from the set of all possible foci at the output of the circuit. As an example of this, Fig. 2b shows the intensity images demonstrating the operation of the Fourier circuit ${\mathbb{F}}$ in d = {2, 3, 5}. This circuit simultaneously transforms the first mutually unbiased basis (MUB) (μ = 1) of input macro-pixel modes (indistinguishable by their amplitude) into a basis of spatially localized output modes that can be detected on a camera or suitable single-photon detector array. This can be compared with conventional single-outcome projective measurements ${\hat{\Pi}}_{a}^{\mu}$ (Fig. 2a, Alice), which project a photon in a particular mode a in basis μ via the combination of a holographic SLM (SLM₃) and a single-mode fibre (SMF)^55,66. Such measurements require one to perform d projections to realize a complete measurement, giving them a maximum effective efficiency of 1/d, which is normally even lower due to device loss. We characterize our circuits by preparing a tomographically complete set of classical input modes and performing quantum process tomography (QPT) (Methods), allowing us to calculate their purity and fidelity to an ideal circuit. As a representative example, the Fourier circuit ${\mathbb{F}}$ achieves fidelities of ${{{\mathcal{F}}}}=\{96.9 \% ,90.5 \% ,89.3 \% ,81.4 \% \}$ in macro-pixel dimensions d = {2, 3, 5, 7}, respectively (Supplementary Information shows the extended results).

Applications of quantum gates

We utilize our programmable circuits to manipulate and certify spatially entangled two-photon states in a range of dimensions, namely, d = {2, 3, 5, 7}. As shown in Fig. 2a, the two photons are generated via the process of spontaneous parametric downconversion (SPDC) and sent to two parties, Alice and Bob. Bob’s photon is locally manipulated by the programmable circuit ${\mathbb{T}}$, whereas Alice’s photon is detected via single-outcome projective measurements ${\hat{\Pi}}_{a}^{\mu}$. Although we have verified the operation of our circuits ${\mathbb{T}}$ with classical light, it is important to repeat this process with our entangled source due to slight differences between their spectral/spatial modes and experimental alignment. Here, instead of using standard QPT, we use the lesser-known method of ancilla-assisted quantum process tomography (AA-QPT)^38,67. AA-QPT uses a single, well-characterized and sufficiently strongly correlated state supported on an extended Hilbert space, along with a tomographically complete measurement, to fully characterize a process. This exploits channel-state duality in which a channel—acting only on one photon from an ideal maximally entangled biphoton state—is fully characterized by the resultant output state, called the Choi state. In the case of non-ideal input states, the Choi state of the channel can still be recovered⁶⁸. Methods provides more details on QPT and AA-QPT.

We first characterize the input state in each dimension using quantum state tomography (QST). We then use these states to recover the Choi states of the processes corresponding to the programmed circuits via AA-QPT. We also perform QST of the output states after operation by the circuits, directly enabling the certification of properties contingent on both input state and process, such as their entanglement and purity. Once the input states, output states and Choi states of the processes are characterized, one can verify and quantify their performance via their fidelity to the ideal states (as defined in Methods). In this manner, our process fidelities quantify how close to ideal our circuits are, taking into account the non-maximally entangled nature of the input entangled state, whereas our output-state fidelities allow independent verification that they preserve high-dimensional entanglement. To quantify the effect of measurement imperfections on our tomographic procedures, we perform an independent characterization of the measurement apparatus, as well as a Monte Carlo sampling of these imperfections in QST and AA-QPT (Supplementary Information) to arrive at realistic error bounds on these fidelities.

To showcase the versatility of our platform, we program 296 instances of all the gates, sampling from different output foci in different dimensions and input bases. Figure 3 (top row) shows examples of normalized two-photon coincidence count data in all MUBs for five-dimensional ${\mathbb{I}}$, ${\mathbb{Z}}$, ${\mathbb{X}}$, ${\mathbb{F}}$ and ${\mathbb{R}}$ gates programmed for the macro-pixel basis. Figure 3 (bottom row) shows the density matrices of the Choi states reconstructed from these data, presenting a clear agreement with the theoretical prediction (insets). The fidelity of the processes, quantified through the fidelity of the experimental Choi states to the ideal Choi states, is reported in Table 1 for all dimensions in the macro-pixel basis. Supplementary Information provides the fidelity of the output biphoton states to an ideal transformed state, their purity and certified entanglement dimensionality, along with an estimation of the systematic errors arising from the measurement apparatus. It is noteworthy that all the output states are seen to preserve high-dimensional entanglement after operation by the gates. For instance, the output state after the identity gate ${\mathbb{I}}$ has a fidelity of ${{{\mathcal{F}}}}({\,\rho }_{\rm{o}},\left\vert {{{\varPhi }}}^{+}\right\rangle \left\langle {{{\varPhi }}}^{+}\right\vert )$ = 85.3 ± 0.7% to the maximally entangled state, which exceeds the bound of 80% necessary to certify five-dimensional entanglement (the fidelity of any state ρ to a maximally entangled target state $F(\,\rho ,\left\vert {{{\varPhi }}}^{+}\right\rangle \left\langle {{{\varPhi }}}^{+}\right\vert ) > k/d$ implies an entanglement dimensionality of at least k + 1 (ref. ⁴⁰)). Supplementary Information presents the results for gates implemented in the orbital angular momentum basis.

Fig. 3: Manipulation and certification of high-dimensional entanglement.

Normalized two-photon coincidence counts (top row) and reconstructed Choi state density matrices (bottom row) corresponding to the operation of identity ${\mathbb{I}}$, Pauli ${\mathbb{Z}}$, Pauli ${\mathbb{X}}$, Fourier ${\mathbb{F}}$ and random unitary ${\mathbb{R}}$ gates on an input two-photon, five-dimensional entangled state in the macro-pixel basis. The two-photon coincidences are measured in all the six MUBs, namely, μ ∈ {0…5}, via projective measurements at Alice and Bob. Due to state–channel duality, measurements on the input and output two-photon states can be used to perform AA-QPT of the gates themselves^38,67. The fidelities of the reconstructed Choi states are reported in Table 1. The identity and Fourier gates enable our circuit to be used as a multioutcome measurement device in MUBs μ ∈ {0, 1} (red squares), allowing us to certify five-dimensional entanglement using the channel itself as a measurement device (see the main text for details). The legend for the density matrix captures both amplitude (brightness, normalized for clarity) and phase (colour).

Source data

Table 1 Quantum process fidelities of inverse design experimental gates to the ideal gates in the macro-pixel basis

Although we have verified that these gates are able to manipulate and preserve high-dimensional entanglement, we now demonstrate how they can be used for the certification of high-dimensional entanglement. Our programmable circuit functions as a generalized multioutcome measurement device, allowing measurements to be made both in the pixel basis μ = 0 (via identity gate ${\mathbb{I}}$) and its first MUB, namely, μ = 1 (via Fourier gate ${\mathbb{F}}$), with an appropriate single-photon detector array. The data for coincidence counts corresponding to a two-basis measurement obtained by programming the circuit in this manner are highlighted in Fig. 3 (red squares). However, as evident from Table 1, our gates are not perfect. Recent work has shown how even slight imperfections in a measurement can compromise entanglement witnesses that normally assume perfect measurements⁶⁹. Thus, it becomes necessary to take these imperfections into account when investigating the detection of entanglement. As described in Methods, we employ a computational approach using semidefinite programming (SDP) to show that our experimentally measured data can only be reproduced by a quantum model that relies on five-dimensional entanglement. Our method takes reasonable statistical and systematic errors into account and yields a quantitative certificate of the entanglement dimension that is also robust to noise. In this manner, we demonstrate how the multimode optical fibre can be used to both transport as well as certify high-dimensional entanglement. It is important to note that, in general, the programmability of our circuit allows for measurements in multiple or even ‘tilted’ MUBs⁴⁰ corresponding to a non-maximally entangled target state, which would lead to increased fidelities and robustness to noise.

The coincidence image (Fig. 2, inset) also provides information about scattering loss outside the output modes of interest. This allows us to measure the success probability of the gate operation, which is defined as the ratio of coincidence counts in the target output modes over the total coincidence counts integrated over all outputs in one polarization channel. We perform this measurement on three randomly chosen implementations of the gate ${\mathbb{F}}$ in two, three and five dimensions and measure a success probability of 0.36 ± 0.01, 0.27 ± 0.03 and 0.18 ± 0.04, respectively (Methods provides additional details). It is worth noting that for this proof-of-concept demonstration, we only control a single polarization channel of the MMF, thus reducing the success probability by about half. Controlling both polarization channels of the MMF can increase the success probability by almost a factor of two as well as improve the fidelity of the implemented circuits. Errors in the fidelities are calculated by taking into account the photon-counting statistics as well as systematic errors due to misalignments. Supplementary Information provides a detailed analysis of misalignments in the measurement apparatus and their effect on the reported fidelities⁷⁰ for both QST and AA-QPT.

Programmability and scalability

We have successfully demonstrated the ability to perform various gates in multiple spatial-mode bases in two, three, five and seven dimensions. However, as the dimension of the target gate increases, maintaining high fidelities and success probabilities becomes increasingly challenging. It is, thus, imperative to examine the programmability and scalability of our design and address ways to improve its performance and target practical experimental regimes to work in. We numerically investigate these by simulating a circuit based on equation (1) and varying three major design parameters—the dimension of the mode mixers n, the dimension of the target gate d and the depth of the circuit L. Multiple implementations of the ${\mathbb{I}}$, ${\mathbb{X}}$, ${\mathbb{Z}}$, ${\mathbb{F}}$ and ${\mathbb{R}}$ gates are simulated for specific values of the design parameters by changing the random unitary mode mixers and the sets of input and output modes for each instance. For each gate, we calculate the fidelity with respect to the ideal target gate and success probability.

We address the following key design considerations: what dimension of mode mixers (n) should be chosen? How many layers (L) are practical to use, given the optical losses usually present at interfaces, and the experimental overhead involved? Figure 4a–d depicts the simulation results showing how the fidelity and success probability of the top-down design (n > d) scale as a function of either the dimension of mode mixers (n) or the depth of circuit (L) as the other design parameters are kept constant. The first observation is that increasing the size of the mode mixers (n) increases the circuit fidelity (Fig. 4a). This demonstrates that even when implementing practical low-depth circuits, such as those presented here, high fidelities can be reached, with high-dimensional mode mixers serving as a key resource for this behaviour. Furthermore, for d/n < 0.1, the success probability is approximately constant with n (Fig. 4b), allowing high-dimensional mode mixers to be employed without affecting the success probability.

Fig. 4: Programmability and scalability of top-down optical circuits.

a,b, Fidelity (${{{\mathcal{F}}}}$) (a) and success probability (${{{\mathcal{S}}}}$) (b) of a d-dimensional quantum optical circuit as a function of the dimension of mode mixers (n) for a circuit depth of L = 2. c,d, ${{{\mathcal{F}}}}$ (c) and ${{{\mathcal{S}}}}$ (d) as a function of L for n = 200. e, Plot of fidelity versus the parameter nL/d² in the regime where d/n < 0.1. This plot shows a converging trend towards unit fidelity (${{{\mathcal{F}}}}=1$), demonstrating that full programmability can be achieved by increasing either the mode-mixer dimension n or circuit depth L. The inset shows a plot of the success probability versus parameter L/d, showing convergence to unity when the number of phase planes approaches $L\approx {{{\mathcal{O}}}}(d)$. A sample size of 200 is used to derive the statistics of each data point. The data are presented as mean values ± one standard deviation.

Source data

Alongside this, we observe that increasing the depth of the circuit (L) increases both fidelity and success probability (Fig. 4c–d), generalizing the recent results into the n > d regime^71,72. In practice, however, scaling up the circuit depth introduces experimental overheads in the form of propagation and interface losses as well as the accumulation of errors. In general, we observe that the fidelity increases and converges to unity (Fig. 4e, d/n < 0.1) when the total number of reconfigurable elements nL exceeds the requirement for parameterizing a d-dimensional unitary transform ${{{\mathcal{O}}}}({d}^{2})$, thereby showing a high level of programmability of the top-down design. Furthermore, the convergence of the success probability to unity occurs when the circuit depth is approximately twice the circuit dimension (L ≈ 2d). This is because there are d(n − d) amplitudes in the transformation, which correspond to scattering to modes outside the target output modes. To achieve a unit success probability, all of these must vanish, requiring at least these many controllable parameters. Thus, the top-down approach presents a powerful route to realizing high-fidelity circuits by harnessing the resource of a high-dimensional mode-mixing space (n > d), as well as operating in a practical, low-circuit-depth regime ($L\leqslant {{{\mathcal{O}}}}(d)$). Supplementary Information provides full details of these simulations.

Discussion

We have demonstrated that programmable optical circuits in the transverse spatial domain can be reliably implemented using the top-down approach that incorporates complex scattering processes between reconfigurable phase planes. We verified that these gates preserve quantum coherence by certifying that high-dimensional entanglement persists after gate operations. We also demonstrate how our gates function as a generalized multioutcome measurement device, enabling the MMF channel to transport, manipulate and certify high-dimensional entanglement. Although our numerical simulations demonstrate the scalability of our technique, finding practical physical platforms for its implementation remains an open challenge. Fundamental aspects of circuit design also present important questions, such as proving that the technique can be used for the universal implementation of unitary transformations, deterministic calculations for setting phase shifters and optimization of these circuits for better performance.

Beyond the transverse spatial degree of freedom, our methods readily generalize to other platforms where phase shifters and mode mixers can be realized. For instance, the implementations of top-down designs in integrated optics will be forthcoming as random-mixed waveguides develop and low-loss reconfigurable phase shifters become available^73,74,75. Further developments must also address practical issues including modal dispersion and spatiotemporal mixing that are present in long MMFs and thick scattering media. These obstacles, however, also enable the extension of the top-down circuit design into the spectral–temporal domain^{76,77,78,79,80}. By demonstrating the practical realization of high-dimensional programmable optical circuits—within the transmission channel itself—our work overcomes a significant hurdle facing the adoption of high-dimensional encoding in quantum communication systems, and paves the way for practical implementations of programmable optical circuits in various near-term photonic and quantum technologies including sensing and computation.

Methods

Experimental Details

A continuous-wave grating-stabilized laser (TOPTICA DL Pro HP) at 405 nm is used to pump a periodically poled potassium titanyl phosphate (ppKTP) crystal (1 mm × 2 mm × 15 mm) at 125 mW to generate a pair of orthogonally polarized photons at 810 nm entangled in their transverse position–momentum degree of freedom through the process of Type-II SPDC. A telescope system of lenses is used to shape the pump beam and focus it on the crystal with a 1/e² beam diameter of 1.2 mm. Phase-matching conditions are achieved via temperature tuning the crystal in a custom-built oven that keeps it at 38 °C. Supplementary Information provides more details on the high-dimensional entanglement source.

After the crystal, the pump is filtered out using a dichroic mirror and a band-pass filter (F), whereas the pair of produced photons is separated by a polarizing beamsplitter. The reflected photon (corresponding to Alice) has its polarization rotated from vertical to horizontal with a half-wave plate and made incident on a phase-only SLM (SLM₃; Hamamatsu X10468-02; effective area size, 15.8 × 12.0 mm²; pixel pitch, 20 μm; resolution, 792 × 600; reflection efficiency, ∼90%; diffraction efficiency, ∼75%) that is placed in the Fourier plane of the crystal using a 400 mm lens. The transmitted photon (corresponding to Bob) is sent to a top-down programmable circuit constructed from a two-metre graded-index MMF (Thorlabs M116L02) placed between two programmable phase-only SLMs (SLM_1,2). After reflection from the SLMs, a telescope system and an aspheric lens are used for mode matching the photons to either SMF or MMF collection modes.

Local projective measurements of the transverse spatial photonic modes are made with computer-generated holograms displayed by the parallel-aligned liquid-crystal-on-silicon layer of the SLMs. The computer-generated hologram for a particular spatial mode is displayed on the SLM at each party. If the incident spatial mode is the complex conjugate of the target mode displayed on the hologram, it is converted into a Gaussian mode, which efficiently couples into an SMF positioned in the far field of the first-order diffraction spot. The SMFs guide the filtered photons to superconducting nanowire single-photon detectors (Quantum Opus, Opus One; efficiency, >90% at 810 nm). Coincidence events between the detection of signal and idler photons in the selected modes are registered by a coincidence counting logic (Swabian Time Tagger Ultra) within a coincidence window of 0.2 ns.

Acquisition of transfer matrix

The optical apparatus used for constructing our circuits is described by the transfer matrix T = U₂P₂U₁P₁, where U₂ is a 2f lens system and P_j is the jth phase plane displayed on SLM_j. To construct the circuits, we need to know the transfer matrix U₁ of the 2-m-long graded-index MMF (Thorlabs M116L02; core diameter, 50.0 ± 2.5 μm; numerical aperture, 0.200 ± 0.015). This is measured using the recently developed multiplane neural network technique⁶³, which uses random phase patterns displayed at both ends of the MMF to acquire the fibre transfer matrix without using an external reference field. In contrast with the main experiment, here we use a superluminescent diode along with an 810.0 ± 1.5 nm filter (Semrock LL01-810-12.5) for transfer matrix characterization. The number of spatial modes (n) of a graded-index fibre at wavelength λ in both polarizations depends on its V number as V = 2πaNA/λ, which is a function of core radius a and numerical aperture NA. We search for the transfer matrix U₁ by optimizing

$$\min {\left\vert {I}_{k}-| {U}_{2}{P}_{{2}_{k}}{U}_{1}{P}_{{1}_{k}}{| }^{2}\right\vert }^{2}.$$

(2)

The optimization is based on the gradient descent method fitting the acquired characterization data consisting of random phase patterns on each plane $({P}_{{1}_{k}},{P}_{{2}_{k}})$ displayed on SLM₁ and SLM₂, respectively, and the corresponding measured output speckle intensity images ${\{{I}_{k}\}}_{k}$ (ref. ⁶³). The model of the optical apparatus is implemented in Keras using TensorFlow 2 and complex-number layers developed elsewhere⁸¹. The dataset is prepared in three parts. First, each input mode in a given basis that is supported by the fibre is displayed on SLM₁. These data provide accurate information of |U₁|. In the second part, random superpositions of these input modes are prepared on SLM₁ and sent through the fibre. The output intensity speckles in this part allow for the recovery of the relative phase and amplitude of the transmission coefficient corresponding to a particular output mode. Finally, both SLMs are used for displaying random superpositions of the input and output modes. This final part of the dataset allows for the accurate reconstruction of U₁, including the calibration of the unknown relative phases across the output modes. Note that U₁ includes the associated coupling optics between the first- and second-phase planes and our measurement is limited to one polarization channel of the MMF. The entire measurement takes ∼90 min, primarily limited by the SLM refresh rate and hologram calculation time, which together take up 90% of the total measurement time. The optimization time is ∼1 min performed on a graphics processing unit (GeForce RTX 3060, CPU Intel Core i7-8700, 16 GB RAM).

Construction of linear circuits

Primarily, programming a circuit ${\mathbb{T}}$ is achieved by calculating the phase solutions ${\{{P}_{j}\}}_{j = 1}^{L}$ at each phase plane. The WFM algorithm can do so by iteratively matching the wavefronts of the target input and output optical modes propagating through the device across all the phase planes^25,64,65. First, input arguments that contain a set of input spatial modes ${\{\left\vert {\psi }_{a}({{{\bf{q}}}})\right\rangle \}}_{a = 0}^{d-1}$ labelled in the logical basis by ${\{{\left\vert a\right\rangle }_{{{{\rm{in}}}}}\}}_{a = 0}^{d-1}$, a corresponding set of output spatial modes ${\{\left\vert {\phi }_{a}({{{\bf{q}}}})\right\rangle \}}_{a = 0}^{d-1}$ that is related to the inputs via $\left\vert {a}_{{{{\rm{out}}}}}\right\rangle ={\mathbb{T}}\left\vert {a}_{{{{\rm{in}}}}}\right\rangle$, and a set of transfer functions {U_j} between phase planes are provided to the WFM algorithm.

For each ith iteration, a phase solution at the pth plane is updated in a cyclic manner starting from the first to the last Lth plane and then back from the last plane to the first. At a particular reconfigurable phase plane P_p, the transfer matrix of the optical device T represented in the spatial q basis is decomposed into two sections:

$${{{\bf{T}}}}:= \mathop{\prod }\limits_{j=1}^{L}{U}_{j}{P}_{j}={B}_{p}{P}_{p}{F}_{p},$$

(3)

where ${B}_{p}=\mathop{\prod }\nolimits_{j = p}^{L}{P}_{j+1}{U}_{j}$ and ${F}_{p}=\mathop{\prod }\nolimits_{j = 1}^{p-1}{U}_{j}{P}_{j}$ such that the forward-propagating input mode onto the pth phase plane is represented by |ψ_a,(p)〉 = F_p|ψ_a〉 and the backward-propagating output mode onto the pth phase plane is $\left\vert {\phi }_{a,(p)}\right\rangle ={B}_{p}^{{\dagger} }\left\vert {\phi }_{a}\right\rangle$. The phase mismatch between these input and output modes can then be adjusted by P_p:

$$\left\vert {\phi }_{a}\right\rangle ={B}_{p}{P}_{p}{F}_{p}\left\vert {\psi }_{a}\right\rangle \ \Rightarrow \ \left\vert {\phi }_{a,(p)}\right\rangle ={P}_{p}\left\vert {\psi }_{a,(p)}\right\rangle .$$

(4)

Considering all d-target modes of interest, the matching matrix ${M}_{p}:= \mathop{\sum }\nolimits_{a,{a}^{{\prime} } = 0}^{d-1}\left\langle {\phi }_{{a}^{{\prime} },(p)}\right\vert {P}_{p}\left\vert {\psi }_{a,(p)}\right\rangle \left\vert {a}^{{\prime} }\right\rangle \left\langle a\right\vert$ captures the mode mixing at each phase plane. The WFM algorithm maximize Tr(M_p) by calculating a phase solution ${P}_{p}^{[i]}$ from the weighted average of the overlapped fields over all d-target modes as follows:

$${P}_{p}^{[i]}({{{\bf{q}}}})=\exp \left(i\arg \left(\mathop{\sum }\limits_{a=0}^{d-1}{\phi }_{a,(p)}^{[{{{\rm{latest}}}}]}({{{\bf{q}}}})\odot {\psi }_{a,(p)}^{* {{{\rm{[latest]}}}}}({{{\bf{q}}}})\right)\right),$$

(5)

where ⊙ is an element-wise multiplication on the q coordinate (SLM pixels) and ${\phi }_{a,(p)}^{{{{\rm{[latest]}}}}}({{{\bf{q}}}})$ and ${\psi }_{a,(p)}^{* {{{\rm{[latest]}}}}}({{{\bf{q}}}})$ are the latest update of the output and input optical fields at the pth phase plane, respectively, taking into account all the other previous updated phase planes $\{{P}_{p}^{[i]}\}$ in the current iteration in both forward and backward directions. The algorithm is iterated until an appropriate value of gate fidelity (equation (12)) is achieved or saturated.

In our experiment, the following gates are implemented and defined as

$$\begin{array}{llll}{\mathbb{I}}&=\mathop{\sum }\limits_{a=0}^{d-1}\left\vert a\right\rangle \left\langle a\right\vert ,&{\mathbb{Z}}&=\mathop{\sum }\limits_{a=0}^{d-1}\left\vert a\right\rangle {\omega }_{d}^{a}\left\langle a\right\vert ,\\ {\mathbb{X}}&=\mathop{\sum }\limits_{a=0}^{d-1}\left\vert a\oplus 1\right\rangle \left\langle a\right\vert ,&{\mathbb{F}}&=\frac{1}{\sqrt{d}}\mathop{\sum }\limits_{a,b=0}^{d-1}\left\vert b\right\rangle {\omega }_{d}^{ab}\left\langle a\right\vert ,\end{array}$$

(6)

where ω_d = exp(2πi/d) and a ⨁ 1 ≔ (a + 1)modd. Also, ${\mathbb{R}}$ is the random unitary that is sampled from the Haar measure for each implementation.

QST

The characterization of the entangled state both before and after manipulation by the circuits is performed via QST. QST is implemented via an informationally complete set of measurements and numeric inversion of the data, subject to physical constraints. Our projective measurements are related to the ideal measurements by incorporating the detection efficiency ${\eta }_{a}^{\mu }$ of measuring a particular spatial mode $\left\vert {\psi }_{a}^{\,\mu }\right\rangle$ (corresponding to the ath element of the μth basis). This is estimated through the knowledge of the computer-generated hologram and its effect on an incoming spatial mode. The resulting projective measurements are given by ${\hat{\widetilde{\Pi}}}_{a}^{\mu}={\eta}_{a}^{\mu}{\hat{\Pi}}_{a}^{\mu}$, where ${\hat{\Pi}}_{a}^{\mu}=\left\vert {\psi}_{a}^{\,\mu}\right\rangle \left\langle {\psi}_{a}^{\,\mu}\right\vert$ is the ideal projector.

We perform QST via SDP on both input and output states after manipulation by the optical circuits. The SDP imposes data fitting of the non-normalized measurements subject to positive semidefiniteness of state ρ, and unit trace, and reads as

$$\begin{array}{ll}\mathop{\min }\limits_{\rho ,R}&| {{{{\mathcal{C}}}}}_{ab}^{\mu \nu }-R\,{{\mbox{Tr}}}\,({\hat{\widetilde{{{\Pi }}}}}_{a}^{\mu }\otimes {\hat{\widetilde{{{\Pi }}}}}_{b}^{\nu }\rho ){| }^{2}\\ {{{\rm{s.t.}}}}&\rho \ge 0\,,\,\,{{\mbox{Tr}}}\,[\rho ]=1,\end{array}$$

(7)

where ${{{{\mathcal{C}}}}}_{ab}^{\mu \nu }$ is the frequency of the outcome (coincidence count rate) and R is the count rate per integration window. Our local measurement bases are complete sets of MUBs⁸², which are informationally complete for QST⁸³, and constructed as ${\hat{\Pi}}_{a}^{\mu}=\left\vert {M}_{a}^{\mu}\right\rangle \left\langle {M}_{a}^{\mu}\right\vert$ and ${\hat{\Pi}}_{b}^{\nu}=\left\vert {{M}_{b}^{\,\nu}}^{*}\right\rangle \left\langle {{M}_{b}^{\,\nu}}^{*}\right\vert$, where $\left\vert {M}_{a}^{\mu }\right\rangle =\frac{1}{\sqrt{d}}\mathop{\sum }\nolimits_{m = 0}^{d-1}{\omega }_{d}^{am+\mu {m}^{2}}\left\vert m\right\rangle$ on the basis of each implemented circuit, and ω_d = exp(2πi/d) is the dth root of unity. All SDPs are implemented in CVX, running the commercial solver MOSEK. In the experiments, the holograms corresponding to the local measurements made by Bob are displayed on SLM₁ in the case of QST of the initial state, whereas in case of QST of the output state, the corresponding holograms are displayed on SLM₂. For all cases, holograms corresponding to projections made by Alice are displayed on SLM₃.

QPT and AA-QPT

A single, well-characterized and sufficiently strongly correlated state supported on an extended Hilbert space, along with a tomographically complete measurement, can also achieve QPT. This process is known as AA-QPT^38,67. On average, our initial state is close—but not exactly equal—to a maximally entangled state (Extended Data Fig. 1). To determine the underlying quantum process, we must invert the dependence on the initial state to recover the Choi state of the channel, that is, an optical circuit. The initial state can be written as a linear operation ${{{\mathcal{A}}}}$ acting only on party A of a maximally entangled state ρ⁺.

$$\begin{array}{ll}{\rho }^{({{{\rm{in}}}})}&=\mathop{\sum}\limits_{n}{A}^{n}\otimes {\mathbb{I}}{\rho }^{+}{A}^{n{\dagger} }\otimes {\mathbb{I}}\\ &={{{\mathcal{A}}}}\otimes {\mathbb{I}}({\,\rho }^{+})\end{array}$$

(8)

The output state we tomograph depends on both initial state and channel ξ, which acts on party B. The channel and the operator generating the initial state, thus, commute; therefore, the output state can be written as the linear operator ${{{\mathcal{A}}}}$ (from equation (8) above) acting on the Choi state^67,68: ${\rho }_{\xi }:= {\mathbb{I}}\otimes \xi ({\,\rho }^{+})$.

$$\begin{array}{ll}{\rho }_{\xi }^{{{{\rm{(out)}}}}}&={\mathbb{I}}\otimes \xi ({\,\rho }^{{{{\rm{(in)}}}}})\\ &={{{\mathcal{A}}}}\otimes {\mathbb{I}}({\,\rho }_{\xi })\\ \end{array}$$

(9)

Provided ${{{\mathcal{A}}}}$ is invertible, this linear equation can be inverted to recover the Choi state ρ_ξ.

The channel’s Choi state can be recovered by operating the inverse, ${({{{\mathcal{A}}}}\otimes {\mathbb{I}})}^{-1}$, on the output state; however, the resultant Choi state may not correspond to a physical channel. In practice, the channels we program are necessarily completely positive, requiring that the Choi state is positive semidefinite: ρ_ξ ≥ 0.

If our transformations were lossless, the channel would also be trace preserving and the Choi state would obey ${{{\mbox{Tr}}}}_{B}[{\rho }_{\xi }]={\mathbb{I}}$. However, in our case of non-trace-preserving channels, we characterize the normalized Choi state as Tr[ρ_ξ] = 1.

To impose positivity of the recovered Choi state in AA-QPT, the SDP is directly optimized over positive ρ_ξ.

$$\begin{array}{rlr}\mathop{\min }\limits_{{\rho }_{\xi },R}&| {{{{\mathcal{C}}}}}_{ab}^{\mu \nu }-R\,{{\mbox{Tr}}}\,({\hat{\widetilde{{{\Pi }}}}}_{a}^{\mu }\otimes {\hat{\widetilde{{{\Pi }}}}}_{b}^{\nu }{{{\mathcal{A}}}}\otimes {\mathbb{I}}({\,\rho }_{\xi })){| }^{2}&\\ {{{\rm{s.t.}}}}&{\rho }_{\xi }\ge 0\,,\,\,{{\mbox{Tr}}}\,[{\rho }_{\xi }]=1\end{array}$$

(10)

The fidelity of such a non-trace-preserving process then corresponds to that of the process, excluding the explicit dependence on global loss⁸⁴.

Alternatively, QPT can be achieved by preparing and inputting a set of tomographically complete input states into a given process and performing measurements on the output states. This prepared and measured QPT can be accommodated in the same formalism by noting that the measurement of a perfect maximally entangled input state is equivalent, up to normalization, to state preparation. This allows the classical characterization of our gates via the same SDP (equation (10)).

Fidelity, success probability and optical losses

We use two figures of merit to characterize the implemented circuits—fidelity ${{{\mathcal{F}}}}$ and success probability ${{{\mathcal{S}}}}$. The first is the Uhlmann–Josza fidelity between two density matrices:

$${{{\mathcal{F}}}}(\,\rho ,{\rho }_{{{{\rm{o}}}}}):= {\left({{\mbox{Tr}}}\left(\sqrt{\sqrt{\rho }{\rho }_{{{{\rm{o}}}}}\sqrt{\rho }}\right)\right)}^{2},$$

(11)

where ρ_o and ρ can refer to the experimentally recovered normalized but non-trace-preserving Choi state, $\widetilde{{\rho }_{\xi * }}$, and the ideal target Choi state, ρ_ξ $=({\mathbb{I}}\otimes {\mathbb{T}}){\rho }^{+}({\mathbb{I}}\otimes {{\mathbb{T}}}^{{\dagger} })$. The fidelity, thus, implies an accuracy of the implemented circuits. Note that in the case when the experimental and target Choi states are pure $({{{\mathcal{P}}}}:= \,{{\mbox{Tr}}}\,\left({\rho }^{2}\right)=1)$, the implemented circuit can be represented by a rank-one Kraus operator $\widetilde{{\mathbb{T}}}$, and the fidelity reduces to

$${{{\mathcal{F}}}}=\frac{{\left({{\mbox{Tr}}}\left({\widetilde{{\mathbb{T}}}}^{{\dagger} }{\mathbb{T}}\right)\right)}^{2}}{\,{{\mbox{Tr}}}\,\left({\widetilde{{\mathbb{T}}}}^{{\dagger} }\widetilde{{\mathbb{T}}}\right)\,{{\mbox{Tr}}}\,\left({{\mathbb{T}}}^{{\dagger} }{\mathbb{T}}\right)},$$

(12)

which is normalized by the transmittance due to scattering from the d-dimensional space of a circuit into other optical modes. The transmittance is quantified by the second figure of merit, namely, the success probability ${{{\mathcal{S}}}}$ of an implemented circuit:

$${{{\mathcal{S}}}}:= \frac{\,{{\mbox{Tr}}}\,\left({\widetilde{{\mathbb{T}}}}^{{\dagger} }\widetilde{{\mathbb{T}}}\right)}{\,{{\mbox{Tr}}}\,\left({{\mathbb{T}}}^{{\dagger} }{\mathbb{T}}\right)}.$$

(13)

The implemented d-dimensional circuit $\widetilde{{\mathbb{T}}}$ is embedded in T, which lives in the n-dimensional space of the apparatus such that $\widetilde{{\mathbb{T}}}={{{{\bf{P}}}}}_{{{{\rm{o}}}}}{{{\bf{T}}}}{{{{\bf{P}}}}}_{{{{\rm{i}}}}}$, where P_o is the output dimensional reduction and P_i is the input dimensional expansion, which map the circuit from d inputs of interest to n inputs of the optical device and from n outputs of the optical device to the d output modes of circuit, respectively. We aim to use ${{{\mathcal{S}}}}$ to measure the scattering loss that stems from the effect of the top-down circuit design, whereas another optical loss of the apparatus is analysed in the last part of this section. Experimentally, the success probability ${{{\mathcal{S}}}}$ (equation (13)) is estimated on the output x space as

$${{{\mathcal{S}}}}=\frac{1}{d}\mathop{\sum }\limits_{a=0}^{d-1}\int{d}^{\,2}{{{\bf{x}}}}{\left\vert \mathop{\sum }\limits_{b = 0}^{d-1}{\widetilde{t}}_{ab}{\phi }_{b}({{{\bf{x}}}})\right\vert }^{2}=\frac{1}{d}\mathop{\sum }\limits_{a=0}^{d-1}\int{d}^{\,2}{{{\bf{x}}}}\mathop{\sum }\limits_{b=0}^{d-1}\frac{{{{{\mathcal{I}}}}}_{ab}}{{{{{\mathcal{I}}}}}_{a}}{\left\vert {\phi }_{b}({{{\bf{x}}}})\right\vert }^{2},$$

(14)

where ${\widetilde{t}}_{ab}$ is a transmission coefficient given that $\widetilde{{\mathbb{T}}}=\mathop{\sum }\nolimits_{a,b = 0}^{d-1}{\widetilde{t}}_{ab}\left\vert b\right\rangle \left\langle a\right\vert$ and ϕ_b(x) is the bth standard output optical field of the circuit on the output x space. The normalization of ${\widetilde{t}}_{ab}$ is measured by the ratio of optical flux inside the bth output mode of a circuit, that is, ${{{{\mathcal{I}}}}}_{ab}\propto | {\widetilde{t}}_{ab}{| }^{2}$, to the total output optical flux transmitting through the system given the ath input mode ${{{{\mathcal{I}}}}}_{a}:= \int{d}^{\,2}{{{\bf{x}}}}{{{{\mathcal{I}}}}}_{a}({{{\bf{x}}}})$, where ${{{{\mathcal{I}}}}}_{a}({{{\bf{x}}}})\propto | \mathop{\sum }\nolimits_{b = 0}^{n-1}{\widetilde{t}}_{ab}{\phi }_{b}({{{\bf{x}}}}){| }^{2}$. Noting that the optical flux ${{{{\mathcal{I}}}}}_{ab}$ can be moved outside the bracket because the target outputs are foci that are spatially separated and conveniently detected using a coherent light source. For a two-photon entangled state, the success probability is then calculated in a similar way using the outcomes of joint measurements between Alice and Bob, the latter of which performs the measurements $\hat{\widetilde{{{\Pi }}}}({{{\bf{x}}}}):= \eta ({{{\bf{x}}}})\left\vert {{{\bf{x}}}}\right\rangle \left\langle {{{\bf{x}}}}\right\vert$ across the output spatial x space:

$${{{{\mathcal{S}}}}}^{\mu }=\frac{1}{d}\mathop{\sum }\limits_{a=0}^{d-1}\int{d}^{\,2}{{{\bf{x}}}}\mathop{\sum }\limits_{b=0}^{d-1}\frac{{{{{\mathcal{C}}}}}_{ab}^{\mu ,\nu = 0}}{{{{{\mathcal{C}}}}}_{a}^{\mu }({{{\bf{x}}}})}{\left\vert {\phi }_{b}({{{\bf{x}}}})\right\vert }^{2},$$

(15)

where the coincidence counts (${{{{\mathcal{C}}}}}_{ab}^{\mu ,\nu = 0}$ and ${{{{\mathcal{C}}}}}_{a}^{\mu }({{{\bf{x}}}})$) are calibrated by the detection efficiencies for both parties and ${{{{\mathcal{C}}}}}_{a}^{\mu }({{{\bf{x}}}})$ is defined as

$${{{{\mathcal{C}}}}}_{a}^{\mu }({{{\bf{x}}}})=R\frac{1}{{\eta }_{a}^{\mu }\eta ({{{\bf{x}}}})}\,{{\mbox{Tr}}}\,({\hat{\widetilde{{{\Pi }}}}}_{a}^{\mu }\otimes \hat{\widetilde{{{\Pi }}}}({{{\bf{x}}}}){\rho }_{{{{\rm{o}}}}}).$$

(16)

Note that since we perform the experiment in all the input spatial-mode bases, the success probability is averaged over all the input bases as ${{{\mathcal{S}}}}=\mathop{\sum }\nolimits_{\mu = 0}^{d}{{{{\mathcal{S}}}}}^{\mu }/(d+1)$. Moreover, one can show that equation (15) can be reformulated to equation (13) if the maximally entangled input state and process (circuit) are pure.

Finally, the overall transmittance ${{{\mathcal{T}}}}$ of a circuit is measured using the two-photon entangled state at the input and output of a circuit as

$${{{{\mathcal{T}}}}}_{a}^{\mu }=\mathop{\sum }\limits_{b=0}^{d-1}\frac{{{{{\mathcal{C}}}}}_{ab}^{\mu ,\nu = 0}}{{{{{{\mathcal{C}}}}}^{* }}_{ab}^{\mu ,\nu = 0}},$$

(17)

where ${{{{{\mathcal{C}}}}}^{* }}_{ab}^{\mu ,\nu = 0}$ is the coincidence count at the initial state. The overall transmittance ${{{\mathcal{T}}}}={{{\mathcal{S}}}}\times {{{{\mathcal{T}}}}}_{\rm{o}}$ includes the success probability ${{{\mathcal{S}}}}$ of a circuit and other optical transmittance of the apparatus, ${{{{\mathcal{T}}}}}_{\rm{o}}$.

High-dimensional entanglement certification with systematic errors

The fidelity and purity of the gates (Table 1 and Supplementary Information) show that our circuits are not perfect (${{{\mathcal{F}}}}$ < 100%). Recent work has shown that even slight imperfections in measurements can compromise entanglement witnesses that normally assume perfect measurements⁶⁹. Here we investigate whether entanglement can be detected and quantified from the relative frequencies corresponding to our data measured in two approximately conjugate bases (Fig. 3, red squares). Focusing on the case of five dimensions, we address the question of whether there exists some bipartite quantum state ρ_AB whose Schmidt number is no more than s, which can model the measured relative frequencies. Since the data must admit a quantum model with some quantum state, which has a corresponding Schmidt number, a negative answer implies that the state is entangled and that its Schmidt number is at least s + 1.

Knowledge of the precise noise present in our experiment can lead to stronger entanglement criteria^85,86, but since we do not know the relevant noise, we adopt an approach where the state is treated as uncharacterized. In our analysis, we assume that Alice’s measurements correspond to the computational basis and the first MUB, respectively. Thus, for Alice, we associate the measurement operators A_a|0 = |a〉〈a| for the first setting and ${A}_{a| 1}=\left\vert {M}_{a}^{1}\right\rangle \left\langle {M}_{a}^{1}\right\vert$ for the the second setting. Here Alice’s outcome can take values a = 0,…, d − 1. On Bob’s side, the positive operator-valued measures (POVMs) {B_b∣ν} for ν = 0, 1 are inferred from the tomographic data. Importantly, Bob’s measurement operators corresponding to the relevant outcomes b = 0, …, d − 1 are incomplete because the measurement features outcomes that are not accessible in the lab. We, therefore, complete Bob’s measurements ad hoc by associating the additional measurement operator ${B}_{d| \nu }={\mathbb{1}}-\mathop{\sum }\nolimits_{b = 0}^{d-1}{B}_{b| \nu }$ to the inaccessible outcome. In a quantum model, we expect the probabilities to follow Born’s rule:

$${p}_{\rm{Q}}(a,b| k)=\,{{\mbox{Tr}}}\,\left({{{{\mathcal{B}}}}}_{abk}{\rho }_{AB}\right),$$

(18)

where ${{{{\mathcal{B}}}}}_{abk}={A}_{a| k}\otimes {B}_{b| k}$. Naturally, however, neither Alice’s nor Bob’s measurements above are flawlessly characterized. In other words, the probabilities p_lab(a, b|k) inferred from the measured relative frequencies for the events a, b ∈ {0, …, d − 1} will not exactly correspond to the given POVMs. Consequently, when addressing whether the underlying state must be entangled, we cannot even expect that there exists any quantum state such that p_Q(a, b|k) = p_lab(a, b|k). This is a well-known drawback of standard entanglement witnessing. To address this issue, we must allow for p_Q to reproduce p_lab up to a reasonable accuracy, which accounts for the imperfections in the estimation of the lab POVMs of Alice and Bob and the photon-counting statistics. Specifically, for each probability associated with the tuple (a, b, k), we introduce a tolerance interval t_abk such that

$${p}_{\rm{Q}}(a,b| k)-{t}_{abk}\le {p}_{{{{\rm{lab}}}}}(a,b| k)\le {p}_{\rm{Q}}(a,b| k)+{t}_{abk}.$$

(19)

We determine the tolerances due to systematic and statistical errors in our experiment from both our measurement devices and our gates’ tomography, via a Monte Carlo simulation of our experiment (Supplementary Information). From multiple simulations of the experiment, corresponding to p_j(a, b|k), for each (a, b, k), we compute the mean deviation from p_lab and its standard deviation, that is,

$${{{\Delta }}}_{abk}=\frac{1}{N}\mathop{\sum }\limits_{j=1}^{N}{X}_{abk}^{\,(\,j)},$$

(20)

$${\sigma }_{abk}=\sqrt{\frac{1}{N}\mathop{\sum }\limits_{j=1}^{N}{\left({{{\Delta }}}_{abk}-{X}_{abk}^{\,(\,j)}\right)}^{2}},$$

(21)

where ${X}_{abk}^{\,(\,j)}=| {p}_{{{{\rm{lab}}}}}(a,b| k)-{p}_{j}(a,b| k)|$ is the deviation in the sample j for the tuple (a, b, k). We evaluate the standard deviation of p_j(a, b|k)_0<j<N for all a, b and k and find that this converges at N ≈ 1,500, allowing us to safely choose N = 2,000. We then choose the tolerance for each and every tuple (a, b, k) to be three standard deviations above the mean deviation from p_lab. Hence, we put t_abk = Δ_abk + 3σ_abk.

With reasonable errors accounted for in the quantum model, we now wish to address whether entanglement is necessary to model the results of the experiment. Specifically, does there exist a p_Q value as given in equation (18) generated from state ρ_AB whose Schmidt number is at most s, such that it reproduces p_lab within the tolerances (equation (19))? This question is both hard to solve and phrased as a binary decision. Although we will soon address the former, we first emphasize that it is favourable to replace the latter with a quantitative statement because one can consequently estimate the confidence in the falsification of the hypothesis (namely, the answer is positive). For that purpose, we introduce additional noise to our measured data p_lab. Specifically, we consider a mixture of our experimental results p_lab, with the probabilities obtained from probing the POVMs of Alice and Bob with a maximally mixed state. The mixing parameter is v ∈ [0, 1]. This gives the artificially noisy probability distribution

$${p}_{{{{\rm{noise}}}}}(a,b| k)=v{p}_{{{{\rm{lab}}}}}(a,b| k)+(1-v)\frac{{{{\rm{Tr}}}}{B}_{b| k}}{{d}^{2}}.$$

(22)

Clearly, the experimental data corresponds to v = 1. Now, we can use v as a quantifier for a model in which ρ_AB has a Schmidt number of at most s. That is, we solve

$$\begin{array}{rl}\max &v\\ {{{\rm{such}}}}\,{{{\rm{that}}}}&{p}_{\rm{Q}}(a,b| k)={{{\rm{Tr}}}}\left({{{{\mathcal{B}}}}}_{abk}{\rho }_{AB}\right)\\ &{p}_{{{{\rm{noise}}}}}(a,b| k)\ge {p}_{\rm{Q}}(a,b| k)-{t}_{abk}\\ &{p}_{{{{\rm{noise}}}}}(a,b| k)\le {p}_{\rm{Q}}(a,b| k)+{t}_{abk}\\ &{{{\rm{Tr}}}}\left({\,\rho }_{AB}\right)=1\\ &{\rho }_{AB}\in {{{{\mathcal{S}}}}}_{s}\\ &{\rho }_{AB}\succcurlyeq 0,\end{array}$$

(23)

where ${{{{\mathcal{S}}}}}_{s}$ is the set of all bipartite states of local dimension d with Schmidt number at most s. Note that any value v < 1 implies that an amount of noise corresponding to a rate 1 − v must be additionally added to the experimental data in order for it to admit a model for Schmidt number s. In other words, it implies that no model based on Schmidt number s is possible and hence a Schmidt number at least s + 1 is necessary.

As mentioned previously, it is difficult to solve equation (23) because the characterization of ${{{{\mathcal{S}}}}}_{s}$ is challenging. However, it is sufficient for our purposes to relax ${{{{\mathcal{S}}}}}_{s}$ into a larger set but over which computations can be efficiently done. It is well known that ${\rho }_{AB}\in {{{{\mathcal{S}}}}}_{s}$ implies that^87,88

$$\left({{\mathbb{1}}}_{d}\otimes {R}_{\frac{1}{s}}\right)({\,\rho }_{AB})\succcurlyeq 0,$$

(24)

where ${R}_{\alpha }(\,\rho )={{{\rm{Tr}}}}\left(\,\rho \right){{\mathbb{1}}}_{d}-\alpha \rho$ is the generalized reduction map. If we replace the condition ${\rho }_{AB}\in {{{{\mathcal{S}}}}}_{s}$ with equation (24), we will obtain an upper bound on equation (23) that is computable as an SDP. We have evaluated this SDP for Schmidt numbers s = 1, 2, 3, 4 and 5 and obtained the following results:

$$\begin{array}{rcl}&s=1\quad \Rightarrow &v\le 0.7068\\ &s=2\quad \Rightarrow &v\le 0.8219\\ &s=3\quad \Rightarrow &v\le 0.9138\\ &s=4\quad \Rightarrow &v\le 0.9924\\ &s=5\quad \Rightarrow &v\le 1.0000.\end{array}$$

(25)

Note that s = 1 corresponds to a separable model and that s = 5 corresponds to a generic five-dimensional entangled state, as was used in the experiment. We conclude that within the estimated tolerances, no quantum model for p_lab exists that relies on less than five-dimensional entanglement. Thus, we certify the Schmidt number as s = 5. In particular, only an additional noise rate of 0.0076 is needed to enable a model based on s = 4. Thus, if we were to somewhat increase the tolerance interval, for example, from 3σ above the mean to 4σ above the mean, then the certified Schmidt number would decrease to s = 4. In either case, the data obtained by applying the ${\mathbb{I}}$ and ${\mathbb{F}}$ gates on our input state certify high-dimensional entanglement.