Main

Rotating turbulence plays an important role in systems such as planets’ atmospheres1,2,3, turbomachinery4, rotating quantum gases5 and neutron stars6,7. Generally speaking, rotating flows of incompressible classical fluids can be characterized by two dimensionless numbers: the Reynolds number \({{{\rm{Re}}}}\) denoting the ratio of inertial to dissipative forces, and the Rossby number Ro expressing the ratio of inertial forces to the Coriolis force. In the limit \({{{\rm{Re}}}}\gg 1\) the flow becomes turbulent, while for Ro ≪ 1 the rotational effects are important. In superfluids, the Rossby number can be defined in a similar fashion as in classical fluids, while the physical meaning of the Reynolds number is captured by the superfluid Reynolds number \({{{{\rm{Re}}}}}_{\alpha }\) (ref. 8), which only depends on intrinsic mutual friction parameters that describe the coupling between the quantized vortices and the normal component9. Theoretical10, numerical11 and experimental12,13,14,15 work suggests that, in classical fluids, rotating turbulence, for which \({{{\rm{Re}}}}\gg 1\) and Ro ≪ 1, could be described as an ensemble of interacting inertial waves (IWs) plus a broadband turbulent component, especially for frequencies exceeding twice the angular velocity. The measurements presented here cover Ro ≈ (1−3) × 10−2 and \({{{{\rm{Re}}}}}_{\alpha } \approx 1{0}^{3}\mathrm{-}1{0}^{5}\), which puts our experimental conditions well within the IW turbulence regime.

Quantum turbulence is usually considered as a complex dynamic tangle of reconnecting quantized vortices16,17,18,19. In the regime \({{{{\rm{Re}}}}}_{\alpha }\gg 1\) and Ro ≪ 1, quantized vortices are nearly parallel and inter-vortex reconnections are suppressed20, exposing the underlying wave-turbulent energy cascade to experimental observation. At the largest length scales, the superfluid flow field may mimic that of classical IWs via collective motion of quantized vortices. Contrary to classical fluids, in superfluids the spectrum of waves extends beyond the IW cutoff frequency (Fig. 1a), as Kelvin waves21,22 (KWs) carried by individual vortices. The crossover between these regimes takes place at kzℓ ≈ 0.5, where kz is the axial wavevector and ℓ is the mean inter-vortex distance set by the angular velocity.

Fig. 1: Experimental principles.
figure 1

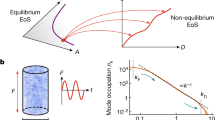
a, In superfluids, for fixed radial wavenumber, the full dispersion relation (blue line) extends beyond the classical IW regime (red line) with a cutoff frequency of 2Ω (dashed black line) set by the angular velocity Ω (Supplementary Discussion 3). Here, ω is the angular frequency of the wave mode. b, A smooth-walled quartz-glass cylinder, filled with superfluid 3He-B, is rotated about its longitudinal axis. During the experiments, we monitor the vortex configuration at two locations using two pairs of NMR pick-up and excitation coils. The quartz glass container is open from the bottom to a heat exchanger volume with rough silver-sintered surfaces. c, The spatial distribution of vortices is monitored with a magnon BEC, trapped in the axial direction in a minimum of the magnetic field H and in the radial direction by spatial variation of the spin–orbit energy (called texture). The radial trapping potential is modified by the presence of vortices. d, We use pulsed NMR to probe the ground-state frequency in the magneto-textural trap. The frequency is shown as the shift from the Larmor frequency fL. The relaxation rate of the signal depends on the vortex density34, while the final frequency (dashed line) is affected by the orientation of vortices (Supplementary Discussion 1).

Full size image

To highlight differences between classical and quantum turbulence, the low-temperature limit is of particular interest since negligible frictional forces allow transfer of energy to length scales where quantization of vorticity is essential19,23. In this limit, the energy is believed to flow towards the smallest scales through a cascade of KWs24,25 or through a quantum stress cascade26 and is ultimately dissipated via emission of sound waves27, emission of quasiparticles28,29 or, at a finite temperature, mutual friction9,30. Despite observations of vortex reconnections and the related production of KWs31,32, direct experimental proof of the existence of the KW cascade has remained elusive.

In the experiments, we initially rotate the sample volume (Fig. 1b) with a constant angular velocity to create an array of quantized vortices with aerial density ℓ−2 oriented along the axis of rotation. We monitor the vortex configuration independently at two spatially separated locations (Fig. 1c) via pulsed NMR techniques (Fig. 1d). We then perturb the vortex array by applying a time-dependent angular drive Ω(t) = Ω0 + Ω1f(ωext), where Ω0 is the mean angular velocity during the drive with amplitude Ω1 < Ω0, and f denotes a triangle wave in the range [−1, 1] with period \(p=2\uppi {\omega }_{{{{\rm{ex}}}}}^{-1}\). During the drive, the following forces are exerted on the vortices: the force due to mutual friction, the Magnus force and the force due to pinning of the vortex ends at the rough bottom of the container. Elsewhere, the smooth walls of the cylinder allow nearly frictionless vortex sliding33. We note that, while the upper spectrometer is located much closer to a surface than the bottom one, the response to the drive (Fig. 2a) is observed first in the bottom spectrometer. This suggests that the coupling between the quantized vortices and the (smooth) top surface is negligible in comparison with that between the vortices and the (rough) bottom surface. Even smoother surfaces may be produced in cold atom experiments, where a uniform trapping potential can be provided by repulsive laser light.

Fig. 2: Buildup and decay of rotating quantum wave turbulence.
figure 2

a, Modulation of the angular velocity (top panel) results in a propagating front of increasing vortex tilt, seen as a frequency shift in NMR measurements (middle panel). The front velocity and saturation time of the signal are explained by the dynamics of IWs (Supplementary Discussion 4). The NMR relaxation rate in the lower spectrometer (bottom panel) shows no observable change in the response to the drive, indicating that the vortex density remains constant during this time34. b, At time tstop, the drive is ramped to a final angular velocity Ωf using the same acceleration \(\dot{\varOmega }\) as during the modulations. After that, an initial period of duration tg, during which the average vortex tilt angle θ remains at a level comparable to the developed turbulence, is followed by an exponential decay towards the equilibrium state. Our estimate (Supplementary Discussions 1 and 7) for the mean vortex tilt angle within the upper spectrometer in units of \({\sin }^{2}\theta\) is shown on the right axis. a and b correspond to the same experimental run with tstop ≈ 1.0 h. c, We utilize vortex filament simulations to visualize our experiment. In the simulations, vortex lines (red) in a cylindrical container (light blue, L = 50 mm) are driven out of equilibrium by applying a drive similar to that in the experiments. In simulations, the vortices couple to the drive via a thin layer with high mutual friction at the bottom (dark blue). The figures are not drawn to scale. The mean inter-vortex distance is ℓ ≈ 0.1 mm. The horizontal alignment of the figures corresponds to the state of the experiment immediately above.

Full size image

Soon after we start the time-dependent drive, we observe a decrease in the measured NMR frequency (Fig. 2a) resulting from an increased average vortex tilt angle with respect to the axis of rotation, denoted by θ (Supplementary Discussion 1). Notably, a propagating wavefront originates from the bottom of the container with phase velocity Vprop ≈ 0.3 cm s−1. This velocity agrees with the phase velocity of the first axially symmetric radial inertial wave mode, Vph = ωex/kz ≈ 0.25 cm s−1. Simultaneously, we observe no change in the relaxation rate of the NMR signal, indicating that the vortex density remains constant during this time34. These observations are in sharp contrast to spin-down measurements with the same experimental setup9,35, where the container is abruptly brought to rest. In response to the spin down, the total angular velocity of the superfluid relaxes towards zero and the initial equilibrium vortex configuration quickly turns to 3D quantum turbulence governed by vortex reconnections and characterized by t−3/2 decay of the vortex line length.

During the drive, the action of hydrodynamic forces on a vortex would far exceed the maximum pinning force, equal to the vortex tension Tv ≈ 10−8 cm g s−2. In this case, vortices are inevitably stretched and the rotating superfluid forms a quantum boundary layer, previously discussed in ref. 36, in which each vortex is acted upon with force equal in magnitude to Tv. We describe the flow of energy in such a system using a phenomenological model (Supplementary Discussion 2) in which the quantum boundary layer pumps energy to a cascade of IWs37, which in turn feeds a cascade of KWs. In the KW regime, the energy is consumed by mutual friction, which also terminates the KW cascade. A qualitatively similar picture is obtained in vortex filament calculations in the presence of a surface layer with increased mutual friction (Fig. 2c). The calculations demonstrate how, in response to the drive, vortices, initially excited at the long wavelength limit, transfer energy towards smaller scales while the role of vortex reconnections is negligible. This process resembles earlier numerical simulations of the cascade of Kelvin waves generated from the excitation of a single KW mode,38 but applied here for a vortex bundle which supports IWs in the long wavelength limit.

After the system has reached a steady state, we stop the drive and ramp the angular velocity to a chosen value Ωf that may differ from Ω0. The vortex array then relaxes from its steady-state configuration with θ ≈ 50° towards the equilibrium state with θ → 0 via a process comprising two clearly distinct stages (Fig. 2b). In the first stage, θ remains at a similar level as during the drive. During this interval, marked as tg, large vortex tilt is sustained by feeding the global flow energy via the quantum boundary layer to IWs (and subsequently to KWs via the IW cascade). The second relaxation stage, an exponential restoration of the equilibrium vortex configuration of the form \({\sin }^{2}\theta \propto \exp (-t/\tau )\) with time constant τ, expected for decaying KWs, is observed after the energy from the global flow has been consumed. This exponential decay is related to dissipation of the energy stored in the KW cascade by mutual friction and qualitatively reproduced in our model calculations (Supplementary Discussion 8 and Supplementary Fig. 8).

The duration of the first relaxation stage is set by the amount of energy stored in the solid-body-like flow and controlled experimentally by varying the final angular velocity Ωf. The characteristic time tg(Ωf) increases with increasing ∣Ωf − Ω0∣ (Fig. 3a). If each vortex is acted upon in a boundary layer with a force equal to βTν in magnitude, the superfluid angular velocity reaches Ωf in a finite time \({t}_{{{{\rm{g}}}}}^{* }={\beta }^{-1}{\tau }_{{{{\rm{s}}}}}\left\vert \ln ({\Omega }_{{{{\rm{f}}}}}/{\Omega }_{0})\right\vert ,\) where τs ≈ 4 × 103 s (Supplementary Discussion 2) and the fitting parameter β ≈ 1 characterizes the energy pumping efficiency. The expression for \({t}_{{{{\rm{g}}}}}^{* }\) agrees with our observations of tg with a single fitted β in the temperature range of (0.13–0.19)Tc, where Tc ≈ 1 mK is the superfluid transition temperature of 3He. Over this temperature range, the dissipative mutual friction parameter α, which controls the energy dissipation rate in the bulk, changes by almost two orders of magnitude9. This temperature independence confirms our picture of the quantum boundary layer feeding the IW energy cascade. As a function of pressure P, the observed change in β (Figs. 3b,c) could be explained by the change in the vortex core size39 with the premise that smaller core size results in enhanced pinning. Furthermore, the complicated dependence of tg on ωex (Fig. 3d) may be understood as additional contributions to the energy of the global flow in the vicinity of standing axially symmetric inertial wave resonances in the cylindrical sample container40,41 and possible generation of geostrophic modes14,15.

Fig. 3: Transfer of energy through the quantum boundary layer.
figure 3

a, The observed relaxation times of the energy stored in solid-body-like rotating flow (symbols) compared with the model of pumping by the quantum boundary layer characterized by the time \({t}_{{{{\rm{g}}}}}^{* }\) (solid black line). Here, Ω0 = 1.6 rad s−1, Ω1 = 0.20 rad s−1, p = 27 s and the fitted energy pumping efficiency is β−1 = 0.57. The data include measurements at pressures of 15.0 and 15.7 bar. We plot the difference tg(Ωf) − tg(Ω0), where tg(Ω0) is separately measured with Ωf = Ω0, to account for any excess energy (such as near-resonant inertial waves or geostrophic modes) not present in our model. Different colours correspond to different temperatures in the range (0.14−0.19)Tc and thus values of the mutual friction parameter α, as marked in the figure. Upwards-pointing triangles correspond to data measured with the upper spectrometer, while downwards-pointing triangles correspond to data from the lower spectrometer. b, The pumping efficiency is found to change with pressure. c, The observed increase of β with pressure (symbols, left axis) may be understood via enhanced pinning with decreasing vortex core size39 (solid line, right axis). d, Measurements of tg with different period of excitation show an increase in the stored energy in the presence of standing inertial waves. The IW cutoff frequency and the modes (M, N), where M is the axial and N is the radial wavenumber, are marked with vertical dashed lines. The error bars in c correspond to 1σ confidence intervals. The estimated error in determining tg is smaller than the symbol size, and errors in a, b and d are not drawn.

Full size image

Let us now turn our attention to the second relaxation stage. For a single KW with a wavevector k, the energy dissipation rate by mutual friction is exponential with a decay rate42 \({\tau }_{{{{\rm{mf}}}}}^{-1}=2\alpha {\nu }_{{{{\rm{s}}}}}{k}^{2}\), where νs ≈ 4 × 10−4 cm2 s−1. On the other hand, for a distribution of KWs in the form of a cascade extending between kstart and kend ≫ kstart, the dissipation remains exponential with a rate given by \({\tau }_{{{{\rm{LN}}}}}^{-1}=\alpha {\nu }_{{{{\rm{s}}}}}{k}_{{{{\rm{start}}}}}^{2/3}{k}_{{{{\rm{end}}}}}^{4/3}\) (assuming a L’vov–Nazarenko KW spectrum;25 Supplementary Discussions 5 and 6). To distinguish between the single-scale and distribution-of-scales scenarios, we study the dependence of the experimental time constant τ−1 on the rotation velocity and temperature. We find that the relaxation rate is linearly proportional to Ωf at a constant temperature (constant α). That is, that \({\tau }^{-1}\equiv {{{\mathcal{A}}}}{\varOmega }_{{{{\rm{f}}}}}\), where \({{{\mathcal{A}}}}\) is a constant (Fig. 4a), suggesting that the dissipative length scale is set by \({\ell }^{-1}\propto \sqrt{{\varOmega }_{{{{\rm{f}}}}}}\). Therefore, in the absence of a cascade for a fixed kℓ (fixed k2/Ωf), \({{{\mathcal{A}}}}\) is expected to scale linearly with α. We find that, at higher values of α (higher temperatures), \({{{\mathcal{A}}}}\) is roughly linear in α (Fig. 4b). In this range, we assume that the dissipation is asymptotically given by a single length scale, that is, kstart = kend. Using values of α from ref. 9 (with α = 0 at T = 0) and the measured values of \({{{\mathcal{A}}}}\), we find kstart = 2.3ℓ−1. However, the deviation from the linear dependence towards the lowest α (lowest temperatures) implies that the dissipation length scale changes with temperature. In the KW cascade picture, this is naturally explained by extension of the cascade towards larger kend with decreasing α (ref. 30). Setting \({\tau }^{-1}={\tau }_{{{{\rm{LN}}}}}^{-1}\) and using the estimated value for kstart, we obtain the extent of the KW cascade kend/kstart (Fig. 4c). The cascade quickly expands to larger wavevectors for α ≲ 10−4, in agreement with previous numerical simulations43.

Fig. 4: Formation of the KW cascade with decreasing temperature.
figure 4

a, The observed exponential relaxation time scales as \({\tau }^{-1}={{{\mathcal{A}}}}{\varOmega }_{{{{\rm{f}}}}}\). In contrast to the temperature-independent tg (Fig. 3a), the relaxation becomes faster at higher temperatures. Ω1 = 0.2 rad s−1 and \({\varOmega }_{0}{\dot{\varOmega }}^{-1}\approx 53\,{\mathrm{s}}\) were kept constant. The error in τ−1 is smaller than the symbol size, and error bars are not shown. b, The mutual-friction dependence of the relaxation rate normalized to Ωf, that is, the slopes \({{{\mathcal{A}}}}\) in a, deviate from the linear dependence expected for a fixed dissipative length scale (solid line), suggesting that the effective dissipative length scale is changing with temperature as a result of the KW cascade. From data at the lowest temperatures, we estimate the value of the effective kinematic viscosity \({\nu }^{{\prime} }\) (dashed line) (Supplementary Discussion 5). The error bars correspond to 1σ confidence intervals. c, We extract the KW cascade extent (filled symbols and open diamond) in the k space as discussed in the main text. The dot-dashed line corresponds to the single-scale scenario with kend = kstart (same as solid line in b). The cascade extends further in the k space with decreasing α, in line with numerical simulations from ref. 43 (open squares). At the lowest temperatures (α ≲ 3 × 10−5), the KW cascade extends to the length scales smaller than the inter-vortex distance (short dashed line). The largest statistical error from b is shown for the corresponding point (29.1 bar). For other points, the statistical errors are smaller than the symbol size. The highest temperature (26.4 bar) and lowest temperature (9.6 bar) points display the estimated systematic errors (Methods) in α, drawn as capless error bars. Symbol colours in b and c mark different pressures shown in the key in c.

Full size image

Our experimental observations, namely that τ ∝ Ωf ∝ ℓ−2 and that τ tends towards a constant value at the lowest α, are consistent with theoretical predictions20 linking the extent of the KW cascade to the effective kinematic viscosity \({\nu }^{{\prime} }\) used to characterize the energy dissipation rate in quantum turbulence (Supplementary Discussion 5). Using the lowest temperature data in Fig. 4b, we obtain an estimate \({\nu }^{{\prime} } \approx 1{0}^{-6}\kappa\), where κ ≈ 6.6 × 10−4 cm2 s−1 is the quantum of circulation in 3He. The obtained value is five orders of magnitude smaller than for homogeneous and isotropic quantum turbulence44, highlighting the different nature of the turbulent flows. Smaller values of \({\nu }^{{\prime} }\) are generally thought to originate from nearly parallel arrangement of vortices20 and in the absence of vortex reconnections45, both of which are realized in our experiments. We also note that, while a recent theoretical work26 put forward an idea of a ‘quantum stress cascade’ as a possible energy transfer mechanism, our observations—in particular the magnitude of the average vortex tilt θ determined mostly by KWs, the temperature dependence of the dissipative length scale, and the wavevector range of the excited KWs from kstart to kend—imply the picture involving a cascade of KWs. We note that, while we cannot experimentally distinguish between different proposed theoretical models for the KW cascade24,25,38, the qualitative result (extension of the KW cascade further in k-space for lower α) is valid regardless of the model (Supplementary Discussion 6 and Supplementary Fig. 7). In the future, detailed numerical simulations of the suppression of the KW cascade by mutual friction in a setting similar to that in our experiment might allow discrimination between models based on our experimental input. Finally, we note that the outliers in the higher temperature data in Figs. 3 and 4 may indicate that the KW cascade picture changes with increasing temperature for α ≳ 10−3 where the dissipative length scale, set by mutual friction, crosses over from quantum (≲ℓ) to classical (≳ℓ) length scales and the KW cascade is completely suppressed.

In a historical context, our work relates to the centuries-old d’Alembert’s paradox stating that, for incompressible potential flow (applicable also to a superfluid), there is no drag for a body moving with constant velocity within the fluid. The solution to this apparent paradox was introduced by Prandtl, who noted that the coupling between the moving body and the surrounding fluid originates in thin surface layers. For rotating flows in classical systems such as the atmosphere or oceans, as a result of a ‘no-slip’ boundary condition, the surface layer takes the form of an Ekman layer. Our experimental findings in the presence of a rough surface are consistent with a ‘partial-slip’ quantum boundary layer, unique to superfluids, where the magnitude of the applied force per quantized vortex is limited to a constant value. On the other hand, superfluids in the zero temperature limit may allow for experimental realization of the original d’Alembert’s paradox in the presence of a smooth surface or if vortices are immobilized in the whole volume, for example, by a nano-structured confinement46. In this work, the presence of the quantum boundary layer allows us to excite vortex waves, which develop into a novel type of quantum turbulence driven by non-linear interactions between vortex waves instead of vortex reconnections. Finally, the measurements presented in Fig. 4b support the existence of the dissipative anomaly for a cascade of KWs. The dissipative anomaly is also referred to as the zeroth law of turbulence due to its fundamental importance for the turbulence theory, and it states that dissipation should remain finite even in the limit of vanishing viscosity (or infinite Reynolds number). However, its nature and very existence for various forms of turbulence is still an active topic of research47,48.

Methods

Sample geometry and thermometry

Our choice of liquid is the superfluid B phase of 3He, which can be studied by using non-invasive NMR methods and for which the low-temperature limit is experimentally accessible. The sample is confined within a 150-mm-long cylindrical container with \(\varnothing\)5.85 mm inner diameter, made from quartz glass (Fig. 1b,c). To avoid vortex pinning on the walls of the container, its inner surfaces are treated with hydrofluoric acid49. The experimental volume, filled with 3He-B, is open from the bottom for thermal coupling to the nuclear demagnetization stage. The experimental volume contains two commercial quartz tuning forks with 32 kHz resonance frequency, commonly used for thermometry in 3He experiments50,51. The forks are calibrated against the Leggett frequency of 3He-B, found by continuous-wave NMR spectroscopy at 0.37Tc and 0.5 bar. At lower temperatures, we assume that the forks’ behaviour is limited to the ballistic regime of quasiparticle propagation, where the forks’ resonance width behaves as \(\mathcal{C}\), where kB is the Boltzmann constant. The parameter \(\mathcal{C}\) ≈ 10 ± 1.5 kHz is the geometric factor, and Δf0 ≈ 10−100 mHz, determined by comparison with magnetic relaxation of the magnon Bose–Einstein condensate (BEC)52, is the forks’ intrinsic width. The calibration is extrapolated to other pressures assuming \(\mathcal{C}\propto p_{\rm F}^{4}\) (ref. 53), where pF is the Fermi momentum.

NMR spectroscopy

Vortex lines affect the spatial order parameter distribution (texture) in superfluid 3He-B owing to contributions from the vortex cores and superflow around them54. Information about the order parameter texture can be extracted via magnetic quasiparticles, magnons, pumped to a three-dimensional trapping potential with a radiofrequency pulse. The magnons quickly form a uniformly precessing BEC in the trap formed by the order parameter texture in the radial direction and by a minimum of the magnetic field in the axial direction. The amplitude of the NMR signal depends on the number of magnons in the trap, which also affects the frequency of the signal. In rotation and at low temperatures, the lifetime of magnons in the trap is limited by conversion to other spin-wave modes mediated by vortices. Thus, the decay time of the NMR signal is a measure of the vortex line density55. Simultaneously, vortex orientation affects the textural part of the magnon trap and the energy of the ground state in the trap, which modifies the precession frequency of the magnon BEC seen in NMR.

In the measurements, we use a static magnetic field of 25 and 36 mT in the upper and lower spectrometer, respectively. The corresponding NMR frequencies are 830 kHz and 1.2 MHz. The magnetic field is created using coils whose symmetry axis is aligned along the axis of rotation. The NMR pick-up coils are spatially separated along the axis of rotation by 90 mm, oriented perpendicular to one another and perpendicular to the axis of rotation. The upper pick-up coil is made of copper wire and is a part of the tank circuit with a quality factor of Q ≈ 1.5 × 102. The lower pick-up coil is made of superconducting wire and is a part of the tank circuit with a quality factor of Q ≈ 7.5 × 103. We use cold pre-amplifiers, thermalized to a bath of liquid helium, and room-temperature pre-amplifiers, to improve the signal-to-noise ratio in the measurements.

Rotating refrigerator

The sample can be rotated about its vertical axis with angular velocities up to 3 rad s−1, and cooled down to approximately 150 μK by using a ROTA nuclear demagnetization refrigerator. The refrigerator is well balanced and suspended against vibrational noise. The Earth’s magnetic field is compensated using two saddle-shaped coils installed around the refrigerator to avoid parasitic heating of the nuclear stage. In rotation, the total heat leak to the sample remains below 20 pW (ref. 56). The rotation velocity is typically changed with a rate of \(| \dot{\varOmega }| =0.03\,\text{rad}\,\text{s}^{-2}\).

Vortex filament simulations

Vortex filament simulations57,58, based on the Biot–Savart law, are used to support our qualitative interpretation of the experimental observations. The simulations start with 19 vortices distributed in three rings with 1, 6 and 12 vortices, from innermost to outermost ring, respectively. Initially, the vortices are straight and terminate at the top and bottom walls, spanning a total of 50 mm each with spatial resolution of 0.125 mm. We note that this resolution is insufficient to reliably determine the spectrum of KWs from simulations. The initial separation of the straight vortices corresponds to a rotating drive of 1.60 rad s−1. The sample radius is 1 mm, and to reduce the computational complexity, vortices occupy only a fraction of the cross-section of the cylinder. An external periodic drive between 1.40 and 1.80 rad s−1 with acceleration of 0.03 rad s−2 is used to drive the vortices out of equilibrium. Image vortices are used to prevent flow through the boundaries.

The vortices couple to the external drive via mutual friction. The mutual friction parameter takes the value α = 1.77 × 10−3 in the bulk. Additionally, we set α = 2 within a 0.1 mm layer at the bottom (Fig. 2c, dark blue). At α ≫ 1, vortices move with the normal component, which in this simulation is clamped to the container. We found that α = 2 is sufficient to keep vortex ends fixed with respect to the bottom boundary, which emulates pinning as seen in the experiment. In simulations, we observe an upwards-propagating wave similar to the experiments and the eventual development of vortex waves at small scales. We further note that producing a layer with high mutual friction experimentally is possible by applying a suitable magnetic field to create a layer of the superfluid A phase with high mutual friction.

During the drive in the simulations (which was on for 600 s), there are a total of 127 inter-vortex reconnection events (using 40 μm as the reconnection distance), with an average reconnection rate of approximately 2 × 10−3 cm−1 s−1. Averaging over 20 s intervals, the highest reconnection rate per vortex length is approximately 10−2 cm−1 s−1 or about one reconnection every 20 s per vortex. In addition, small-scale structures appear before the first reconnection event takes place, suggesting that inter-vortex reconnections do not play a significant role in the development of the cascade. When the modulation of the rotation velocity is stopped (here, Ωf = Ω0), the vortex configuration decays towards the equilibrium state with parallel straight vortices. To reduce the computation time for illustrative purposes, the two rightmost images in Fig. 2c were obtained by developing the state with higher mutual friction (α = 4.7 × 10−2). In the simulations, we used a core size of a0 ≈ 1.7 × 10−5 mm.

Validity and application of the weak turbulence theory

A cascade of KWs can be described within the framework of weak turbulence theory (WTT)59,60, whose validity has been recently confirmed in experiments61. In principle, WTT can be applied to a variety of systems, both classical61,62,63,64,65,66,67 and superfluid68,69,70,71,72, given that proper experimental conditions are met. Rotating quantum wave turbulence differs from hydrodynamic quantum turbulence73,74,75,76 in that the energy cascade is driven by non-linear interactions between waves instead of vortex reconnections.

According to ref. 77, the squared amplitude of KWs can be estimated from

$${A}_{k}^{2}=2{\left(\frac{2{\pi }^{3}{c}_{{{{\rm{LN}}}}}^{2}}{9}\right)}^{1/5}\frac{{k}_{{{{\rm{start}}}}}^{19/15}{\epsilon }_{{{{\rm{KW}}}}}^{1/5}}{{\kappa }^{3/5}{k}^{11/3}},$$
(1)

where \({c}_{{{{\rm{LN}}}}}\approx 0.304\) and ϵKW is the energy cascade rate in the KW cascade. The largest amplitude is at the largest length scale, where k = kstart = 2.3ℓ−1. Taking the estimated energy cascade rate εKW = ϵKWℓ−2 = 2 × 10−6 cm2 s−2 (Supplementary Discussion 5), we get Ak ≈ 28 μm at the largest scale, which is an order of magnitude smaller than the wavelength λk ≈ 392 μm. We therefore believe that, to a good approximation, the WTT condition Ak ≪ λk holds and that WTT should be applicable in our experiment. We use WTT to determine the dependence of \({\tau }_{{{{\rm{LN}}}}}\) on kstart and kend (Supplementary Discussions 5 and 6).

To further confirm the validity of WTT in our experiment, we have tried to limit the fitting of the exponential decay in Fig. 2b to the tail where θ < 35°, corresponding to a ~30% smaller Ak than at the steady state with a tilt angle of θ ≈ 50°. Processing only the tail of the relaxation results in an increase in the scatter of the data without qualitative changes. We therefore fit the whole decay for the purposes of extracting the decay time constant τ.

Systematic errors in the mutual friction parameter α

The dissipative mutual friction parameter α used in the analysis has uncertainties from several sources. The parameter α depends on the temperature via the exponential factor \(\mathrm{e}^{-\varDelta /({k}_{{{{\rm{B}}}}}T)}\) while being linearly proportional to the resonance width of the quartz resonator used as a thermometer50,51. We measure the full resonance curve of the resonator, and extract the temperature from its width. The statistical error in the resonance width is negligible in comparison with systematic errors and can be neglected.

The first source of systematic errors is the conversion from the measured temperature to α. We interpolate in pressure the values of α from ref. 78, where the mutual friction parameter α was measured at several pressures spanning the whole pressure range in this work. We use the theoretically expected pressure dependence for the interpolation, and on the basis of the deviation of the measured points from the theoretical dependence, we estimate that the systematic uncertainty in the conversion of T to α is up to 30%. This uncertainty is the dominant one at higher temperatures (α ≳ 10−4) and is demonstrated by the horizontal error bar in Fig. 4c for the highest temperature (26.4 bar) data point. The corresponding uncertainty in the vertical direction is smaller than the symbol size in the plot and is not shown.

The second source of systematic error, dominant in the low temperature limit, is the uncertainty in the intrinsic (zero temperature) resonance width of the quartz resonator. At the lowest temperatures (α < 10−5, corresponding to T ≈ 0.13Tc at 9.6 bar), we estimate that the resulting error in the temperature is smaller than 0.01Tc. The error bars (both horizontal and vertical) resulting from a change of temperature by 0.01Tc are shown in Fig. 4c for the lowest temperature (9.6 bar) data point. This uncertainty decreases quickly with increasing temperature, as the resonance width of the quartz resonator, which depends exponentially on the temperature, exceeds the estimated intrinsic width by an order of magnitude for α ≳ 10−4.