Abstract
The interplay of quantum statistics and interactions in atomic Bose–Fermi mixtures leads to a phase diagram markedly different from pure fermionic or bosonic systems. However, investigating this phase diagram remains challenging when bosons condense due to the resulting fast interspecies loss. Here we report observations consistent with a phase transition from a polaronic to a molecular phase in a density-matched degenerate Bose–Fermi mixture. The condensate fraction, representing the order parameter of the transition, is depleted by interactions, and the build-up of strong correlations results in the emergence of a molecular Fermi gas. The features of the underlying quantum phase transition represent a new phenomenon complementary to the paradigmatic Bose–Einstein condensate/Bardeen–Cooper–Schrieffer crossover observed in Fermi systems. By driving the system through the transition, we produce a sample of sodium–potassium molecules exhibiting a large molecule-frame dipole moment in the quantum-degenerate regime.
Similar content being viewed by others
Main
Mixtures of interacting bosons and fermions have been the subject of intense research since conventional superconductivity was understood to arise from the effective attraction between electrons mediated by phonons. In solid-state materials, the electron–phonon coupling is captured by Fröhlich or Holstein models. Developments in ultracold atoms1 and van der Waals materials2 now make it possible to realize Bose–Fermi mixtures that are governed by beyond-Fröhlich physics where bosons and fermions can bind to fermionic molecules3,4,5,6,7,8 reaching the quantum-degenerate regime9. The competition between this novel bound state physics and mediated interactions leads to an enriched phase diagram potentially featuring supersolidity and charge-density-wave phases10,11,12,13, molecular Fermi liquids14,15,16,17,18,19 and unconventional boson-induced superconductivity20,21.
Experimentally, the phase diagram of Bose–Fermi mixtures has primarily been explored in the regime of large population imbalance where one species acts as a dilute, thermal gas of impurities dressed by its environment. Bose polarons were recently observed in the limit of fermionic impurities in a bosonic bath22,23,24, while the existence of a transition from Fermi polarons to molecules has by now been firmly established for impurities immersed in a Fermi sea25,26,27,28. However, it has remained unclear how the transition from atoms to molecules proceeds when the impurities are degenerate, in particular when bosons and fermions of comparable density dress each other mutually and drastically modify their respective behaviour. Importantly, this regime of matched particle density is promising for the association of heteronuclear molecules at high phase space density, which finds wide-ranging applications in quantum chemistry and the exploration of dipolar quantum many-body systems29,30. At the same time, reaching this regime is notoriously difficult in double-degenerate mixtures due to the enhanced density of the bosonic condensate. The excess density of the Bose–Einstein condensate (BEC) causes fast interspecies loss, which remains the key bottleneck for reaching quantum degeneracy in heteronuclear molecules and for the study of strongly correlated Bose–Fermi mixtures.
In this Article we investigate strongly interacting Bose–Fermi mixtures with comparable densities. Our data suggest that, in the low-temperature regime where the bosonic impurities condense, strong boson–fermion interactions induce a phase transition from a polaronic condensate to a molecular Fermi gas, connecting to an underlying quantum phase transition (QPT) at T = 0 (ref. 16). Using a novel density-decompression technique that mitigates atomic loss, we produce a double-degenerate Bose–Fermi mixture of 23Na and 40K with matched density and reveal signatures of this QPT. Starting from a weakly interacting mixture, increased attractive interactions dress the bosonic condensate polaronically. By continuously tuning the interaction strength, the polaronic condensate is depleted and a transition into a phase of quantum-degenerate fermionic molecules is observed. Driving the underlying QPT enhances the association efficiency of Feshbach molecules to near unity. This enables the subsequent creation of ground-state 23Na40K molecules with a large molecular-frame dipole moment of 2.7 debye in the quantum-degenerate regime.
Degenerate Bose–Fermi mixtures in density-matched regime
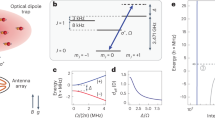
A simplified phase diagram of Bose–Fermi mixtures is illustrated in Fig. 1a as a function of the ratio of boson to fermion density nB/nF and the dimensionless interaction strength 1/kiaBF. Here, aBF denotes the boson–fermion scattering length, and the wavevector ki is determined by the interparticle spacing of the majority species \({{k}}_{i}={(6{\uppi }^{2}{n}_{i})}^{1/3}\), where i denotes B(F) for nB > nF (nB < nF). Phases involving bound states of more than one boson are ignored, as these are intrinsically unstable due to fast recombination loss.
a, Phase diagram of degenerate Bose–Fermi mixtures as a function of the density ratio nB/nF and the dimensionless interaction strength \({({k}_{i}{a}_{\rm{BF}})}^{-1}\). For nB/nF → 0 one attains the Fermi polaron limit, featuring a polaron-to-molecule transition (black diamond), whereas for nB/nF → ∞, the Bose polaron limit with a smooth crossover is reached. For nB < nF, a QPT between a polaronic and a molecular phase of either first order with phase separation or second order is expected. The long-dashed line marks the complete depletion of the condensate \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}\) and, in the case of phase separation, the dotted line marks its onset at \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{{{{\rm{ps}}}}}^{-1}\). The dash-dotted line marks a possible further QPT of unknown order. b,c, Calculated in situ density profiles of bosons (blue) and fermions (red) in the species-dependent 785-nm dipole trap (b) and in the far-detuned trap (c) (Methods). The dashed blue line gives the thermal boson fraction, showing a lack of thermal bosons in regions where bosons and fermions overlap. d, Order parameter ϕ as a function of \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) for the boson–fermion average-density ratio \({\bar{n}}_{\rm{B}}/{\bar{n}}_{\rm{F}}={0.4}\) (orange points) and \({\bar{n}}_{\rm{B}}/{\bar{n}}_{\rm{F}}={0.7}\) (blue points). The error bars are discussed in Methods. The black solid line shows the order parameter from zero-temperature theory in ref. 18, predicting the QPT to occur at \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}={2.02}\) (black triangle) for ideal bosons interacting with a Fermi gas at nB/nF = 1. The red solid line shows the polaron quasiparticle weight of a bosonic impurity in a Fermi gas obtained from a self-consistent fRG calculation that predicts the polaron-to-molecule transition to occur at \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}={1.16}\) (red triangle). e, Energy spectrum of the zero-momentum Fermi polaron (red line) and the zero-momentum molecule (grey line) for a single bosonic impurity obtained from the fRG. The energies cross at the polaron-to-molecule transition (red dashed line). For aBF > 0, the binding energy \({E}_{\rm{b}}={-{\hslash }^{2}/2\mu {a}_{\rm{BF}}^{2}}\) is subtracted, where μ is the reduced mass.
Qualitatively, the phase diagram in Fig. 1a can then be divided into two regimes. In the limit of vanishing Bose–Fermi attraction, \({{({k}_{i}{a}_{\rm{BF}})}^{-1}\to -\infty}\), bosons and fermions decouple and form a BEC along with a Fermi sea. As attractive interactions are switched on, fermions and bosons modify each other’s properties, leading to quasiparticle formation. Due to the polaronic character of this interaction, we denote the resulting phase as the ‘polaronic phase’. In the opposite limit of strong attraction, realized at \({{({k}_{i}{a}_{\rm{BF}})}^{-1}\to \infty}\), for nB ≤ nF, binding of all bosons to fermions leads to a Fermi sea of molecules coexisting with an atomic Fermi sea, and we denote this phase the ‘molecular phase’. For nB ≤ nF, the polaronic and molecular phase are predicted to be either separated by a first-order QPT with phase separation or by a second-order QPT14,16,17,18,31,32. When tuning the density ratio across nB/nF ≈ 1 in the regime of strong attraction, an additional phase transition, where a condensate reappears, is predicted to occur14. This phase featuring molecules and an excess condensate is predicted to cross over into the polaronic phase for nB/nF ≳ 1 (ref. 14). Most experiments have been carried out in the impurity limits either on the far left-hand or the far right-hand side of the phase diagram22,24,25,26,27,28.
A natural way to investigate the phase diagram away from the impurity limits starts from producing a double-degenerate Bose–Fermi mixture. The regime of matched densities is of particular interest, where the system becomes strongly correlated and neither of the atomic species can be regarded as a quantum impurity. To access this novel regime, we employ a species-dependent dipole trap at 785 nm, which is near-detuned to the D-lines of the K atoms. This trap provides a weaker confinement of the Na atoms compared to the K atoms, lowering the density of the Na BEC and increasing overlap between the species (Fig. 1b). As a consequence, the detrimental loss resulting from collisions of Na atoms in the BEC with NaK* Feshbach molecules is dramatically reduced (Methods). In contrast, for a typical trap set-up where the trapping effect is similar for both atomic species, the peak density of the BEC is considerably larger than that of the Fermi gas (Fig. 1c). This results in an entirely different physical regime related to the Bose polaron problem with a low molecule association efficiency when starting from the BEC (Methods).
QPT from a polaronic phase to a molecular phase
In the regime where nB ≤ nF, theory at low temperature predicts a transition from a phase where a BEC coexists with a Fermi gas to a liquid where all bosons are bound into molecules14,16,17,18,31,32. By tuning the interactions from weak to strong coupling, the boson–fermion interaction gradually depletes the BEC until the condensate fraction, representing the order parameter of the transition, vanishes at the critical interaction parameter \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}\), resulting in a phase transition. At this interaction strength for T = 0, a QPT occurs, possibly masked by a phase-separation regime17,31,32. This is a distinct feature in Bose–Fermi mixtures that is absent for the BEC/Bardeen–Cooper–Schrieffer (BEC-BCS) crossover in spin-balanced fermionic mixtures where no symmetry-breaking pattern is changed as the interaction strength is varied across the Feshbach resonance33. Furthermore, in contrast to the BEC-BCS phase, the molecular phase is more robust with respect to temperature16,34,35. In both cases, pairing is required, which is not affected by small temperature fluctuations, as pairing occurs with binding energies on the order of several Fermi energies. In the BEC-BCS phase, however, molecules are additionally required to condense, whereas in Bose–Fermi mixtures they merely need to form a Fermi sea.
The order of the transition depends on the Bose–Bose repulsion aBB and the density ratio nB/nF (refs. 17,31,32). The transition is predicted to be of first order in a large parameter regime, and only beyond a threshold do stronger Bose–Bose repulsion and lower nB/nF favour a second-order transition17,32. Tuning the Bose–Fermi interaction strength \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) from weak to strong interactions at a fixed density ratio nB/nF < 1, the condensate density decreases smoothly and vanishes beyond a critical interaction parameter \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}\) for a second-order phase transition. For a first-order transition, on the other hand, the homogeneous system passes through a phase-separation region. On reaching the lower boundary \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{{{{\rm{ps}}}}}^{-1}\), the system enters a phase-separated state (Fig. 1a), where the local condensate density drops to zero discontinuously in some parts of the system, but remains finite in others. Tuning the interactions further, the mixing ratio between the two phases shifts towards the molecular phase and, once \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}\) is reached, all parts of the system have transitioned to the molecular phase. Importantly, however, the globally averaged condensate density is expected to decrease smoothly and to vanish continuously at \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}\) in both cases. This effect is enhanced by the harmonic trap (Fig. 1b,c), and it makes distinguishing between the two cases challenging.
Within the condensed polaronic phase it is predicted that the depletion of the condensate depends weakly on the boson–fermion density ratio, which, remarkably, extends all the way to the Fermi polaron limit, nB/nF → 0 (refs. 18,28). In the extreme limit of a single bosonic impurity in a Fermi gas, the phase transition connects to a polaron-to-molecule transition, and the condensate fraction reduces to the impurity quasiparticle weight (for a detailed explanation, see ref. 18). A computational, self-consistent functional renormalization group (fRG) technique that takes into account an infinite number of particle–hole excitations of the Fermi sea (Methods)36 predicts this transition to occur at \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}={1.16}\) (Fig. 1e). This transition point is expected to shift to larger values as temperature and boson density increase18,27,37.
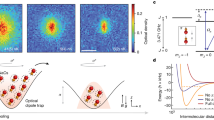
In the following, we probe signatures of this QPT. Our experiment typically starts with \({2.3\times 1{0{}^{5}}}\) 40K atoms at T = 80 nK (corresponding to T/TF ≈ 0.2, where TF is the Fermi temperature) and \({0.8\times 1{0{}^{5}}}\) 23Na atoms with a condensate fraction of 60% at a magnetic field of 81 G. We employ a single magnetic field ramp with a speed of 3.5 G ms−1 (Methods) that is terminated at the desired magnetic field close to a Feshbach resonance at 78.3 G (refs. 38,39), corresponding to different interaction strengths \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\), while the Bose–Bose interaction remains at aBB = 53a0 (ref. 38). Due to the small effective-range parameter kFR* = 0.08 of this broad Feshbach resonance, the Bose–Fermi interactions are characterized by the single parameter \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) (Methods and ref. 38). Throughout the magnetic field ramp, no collapse or immiscibility of the Bose–Fermi mixture are observed on the timescale of the experiment (Methods). Furthermore, we checked that the depletion of the BEC is independent of the ramp speed for the sufficiently slow ramp used here (Methods). This indicates that the system stays close to a local equilibrium state until near the critical point. We then quench the magnetic field to 72.3 G. This projects the system onto free atoms and deeply bound molecules, which are subsequently imaged in time of flight after Stern–Gerlach separation, as shown in Fig. 2a,b.
a, Absorption images showing the optical density (OD) of Na atoms (Na) and Feshbach molecules (NaK*) after 18-ms time of flight during the association ramp from the polaronic BEC to the molecular phase. b, Production of Feshbach molecules. Numbers of condensed Na atoms (dark orange points), thermal Na atoms (bright orange diamonds) and Feshbach molecules (grey points) are shown as a function of \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) for \({\bar{n}}_{\rm{B}}/{\bar{n}}_{\rm{F}}={0.7}\). The red dashed line in b and d indicates the polaron-to-molecule transition at \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}={1.16}\) in the Fermi polaron problem. c, Absorption images during the dissociation ramp with 18-ms time of flight. d, Dissociation of Feshbach molecules. Condensed Na atom (dark orange points), thermal Na atom (bright orange diamonds) and Feshbach molecule (grey points) numbers are shown as a function of \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) for \({\bar{n}}_{\rm{B}}/{\bar{n}}_{\rm{F}}={0.7}\). The error bars are discussed in Methods.
To characterize the phase transition quantitatively, we define the normalized order parameter ϕ = NBEC/(Nm + NBEC). Here NBEC and Nm represent the number of condensed Na atoms and those associated to molecules, respectively. The order parameter ϕ describes the depletion of the condensate fraction due to the excitation of bosons to finite-momentum states by quantum fluctuations. These quantum fluctuations are dominated by the build-up of pairing correlations, measured by the projection onto molecules. Note that, in the definition of ϕ, we disregard thermal Na atoms as we describe the condensate fraction in the centre of the trap. First, the spatial extension of thermal bosons (Fig. 1b) is much larger than that of the BEC and the fermions, both of which are concentrated in the centre of the trap. Here the density of thermal bosons is more than 20 times smaller than that of the BEC. Second, on the timescales of the experiment, thermal bosons do not play a significant role in molecule formation due to their weak spatial overlap with the fermions. Molecules are thus formed predominantly from BEC atoms.
The temperature of bosons in the centre of the trap where most of the boson–fermion collisions take place is thus effectively much lower than suggested by the equilibrium temperature, allowing us to directly compare our findings with zero-temperature theory. Specifically, in Fig. 1d we make a comparison with the quasiparticle weight of a bosonic impurity calculated from a self-consistent fRG approach (Methods)36 (red dashed line) and predictions of the condensate fraction from a non-self-consistent T-matrix (NSCT) theory18 (black solid line) for nB = nF that neglects multiple particle–hole excitations in the Fermi sea.
In Fig. 1d, we show the measured order parameter ϕ as a function of \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) for \({\bar{n}}_{\rm{B}}/{\bar{n}}_{\rm{F}}={0.4}\) and 0.7, where \({\bar{n}}_{\rm{B}}/{\bar{n}}_{\rm{F}}\) denotes the ratio of the average boson and fermion densities in parts of the trap with a finite condensate fraction in the weakly interacting regime. As the interaction strength increases, ϕ reduces slowly for \({{({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1} < 0}\). However, once the scattering length becomes positive, ϕ decreases rapidly and vanishes in the regime beyond \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}={1.44(15)}\) (\({\bar{n}}_{\rm{B}}/{\bar{n}}_{\rm{F}}={0.7}\)) and \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}={1.75(18)}\) (\({\bar{n}}_{\rm{B}}/{\bar{n}}_{\rm{F}}={0.4}\)), where the residual condensate fraction is comparable to the uncertainty of the measurement. Our measurements agree well with the predicted condensate fraction from the NSCT approach throughout the entire interaction regime. Importantly, both datasets overlap within error bars, providing support for the predicted universality of the condensate depletion with respect to varying nB/nF (refs. 18,28). This, in turn, justifies comparing our in-trap experiment with predictions for a homogeneous system. The data also show a remarkable agreement with the quasiparticle weight of a single impurity in most of the interaction regime, except close to the phase transition. This indicates that, despite having a large boson density, the system can be well described as a condensate of polaronically dressed bosons. In contrast, however, at the transition, the order parameter vanishes smoothly compared to a jump predicted in the impurity limit.
To estimate the transition point independently from the slowly varying order parameter, we consider the projected Feshbach molecule number shown in Fig. 2b as a measure of existing boson–fermion pairing correlations (Methods). As \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) increases, so do the pairing correlations (including potential fermion–molecule mixing14), until they saturate when the bosons are fully bound into molecules. The resulting transition point \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}={1.29(14)}\) extracted from the measured Feshbach molecule number is consistent with the transition point obtained through the vanishing of the order parameter.
Driving through the transition provides an efficient method to create molecules. Our data show that a striking conversion efficiency of ~80% of the Na atoms in the BEC into Feshbach molecules can be achieved. Accounting for the residual density mismatch and the resulting interspecies loss from the excess bosons, our data suggest that the entirety of the BEC could be converted into molecules for perfectly matched density conditions. In contrast, the highest conversion efficiency from a BEC previously reported was less than 50% in KRb, where the density of bosons in the centre of the trap was ten times higher than that of the fermions, which was possible only because of the tenfold lower interspecies loss coefficients compared to NaK9,39,40.
Next, we investigate the reversal of the phase transition. After the association ramp reaches \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}={1.3}\), the magnetic field is ramped back to dissociate the molecules. The dissociation ramp is again followed by a magnetic-field quench to 72.3 G for detection. As can be seen from the time-of-flight images in Fig. 2c, the number of projected Feshbach molecules decreases, and a finite BEC fraction is recovered. In particular, we show that the number of Na atoms in the BEC can be increased from 3(2) × 103 to 8(1) × 103 (Fig. 2d). Heating is evident after the dissociation in the form of an increase of thermal Na atoms, which we attribute to the non-adiabatic nature of the magnetic-field ramps near the transition point. Due to the changing number of Na atoms in the thermal wings, we thus cannot characterize the reversal of the phase transition with the order parameter ϕ as done in the association ramp. Nonetheless, the partial restoration of the BEC highlights the coherence preserved in our experiment and is a striking example of how bosons that were bound into fermionic molecules in finite-momentum states are converted back into their motional ground state. Thus, the Fermi degeneracy of the molecules and the partial restoration of the BEC underline the low entropy of our molecular clouds.
Degenerate Fermi gas of NaK* Feshbach molecules
After the preparation 5 × 104 Feshbach molecules at a temperature of 100 nK by ramping across the QPT, we convert them to more deeply bound states by quenching the magnetic field to 75 G. At this magnetic field, we turn on a strong gradient to levitate the molecules and remove any residual atoms from the trap (Methods). Inelastic collisions between molecules are strongly suppressed by Pauli blocking, leading to a second-long lifetime (Methods). The quantum degeneracy of the molecular gas after association is determined by time-of-flight imaging after holding the molecules for 100 ms (Fig. 3), ensuring that collective oscillations induced by the magnetic-field ramps of the molecular cloud are dampened out (Methods). The momentum distribution of the molecules is well described by a Fermi–Dirac distribution9 with a temperature of T = 0.28(1)TF.
a, Velocity distribution of Feshbach molecules. The angular integral (black points) of an average of 15 images with a time of flight of 15 ms (shown in the inset) was fitted with Fermi–Dirac (blue line) and Gaussian (red line) distributions. Although the Gaussian fit overestimates the occupation at lower velocities, the data are well described by a Fermi–Dirac distribution, which accounts for the Pauli blocking. The fit of the Fermi–Dirac distribution results in T/TF = 0.28(1). b, Angular integral of the residuals.
Low-entropy NaK ground-state molecules
The establishment of a means to efficiently create large ensembles of heteronuclear Feshbach molecules sets the stage for the creation of polar ground-state molecules. To achieve this, we coherently transfer the degenerate Fermi gas of 5 × 104 Feshbach molecules into the rovibronic ground state of the X1Σ+ electronic manifold41, with an overall efficiency of up to 60%. The momentum distribution is maintained during the transfer and is still fit well by a Fermi–Dirac distribution at a temperature of T = 0.28(3)TF. However, due to the absence of thermalization and the imperfect transfer efficiency, random holes are created in the molecular Fermi sea. Accordingly, we expect the quantum degeneracy of the ground-state molecular gas to be reduced compared to the Feshbach molecular gas9,42. Hence, as an alternative measure of the degeneracy, we compute the peak occupancy of the Fermi gas f, characterizing the probability of the lowest energy state in the Fermi gas to be occupied. Based on the transfer efficiency to the ground state and the initial degeneracy of the Feshbach molecules, we obtain a peak occupancy of f = 57(3)%, which corresponds to an effective temperature of T = 0.52(2)TF.
Conclusion
Using a species-dependent decompression technique of atomic clouds, we have observed signatures of a QPT in Bose–Fermi mixtures between a phase featuring condensation and a molecular Fermi gas, in excellent quantitative agreement with theory. By driving the system through this phase transition, we have produced a gas of quantum-degenerate Feshbach molecules with record efficiency. The characterized phase transition represents a new phenomenon complementary to the paradigmatic BEC-BCS crossover observed in Fermi systems33 and the atomic-to-molecular BEC crossover in Bose systems43. It is a first step in the exploration of strong-correlation physics in degenerate Bose–Fermi systems and provides a benchmark for their theoretical understanding. The investigation of the order of the transition is an intriguing avenue for future research, such as an observation of hysteresis17 and quantum critical dynamics44 or the exploration of solid-state systems where chemical potentials can be readily tuned2. Our method can be extended to other Bose–Fermi mixtures for producing large degenerate samples of fermionic molecules and may help to achieve a heteronuclear molecular BEC from Bose–Bose mixtures, which suffer from even more severe losses when both bosonic species condense45,46,47,48,49,50. Ultimately, our technique allows us to produce a gas of non-reactive ground-state molecules in the quantum-degenerate regime with five times stronger molecular-frame dipole moments than the first degenerate polar molecules of KRb, and provides excellent conditions for evaporative cooling of ground-state molecules, as demonstrated for KRb51,52 and recently also for NaK53. This opens up exciting opportunities to study strongly correlated dipolar quantum systems54 ranging from the collapse of dipolar Fermi gases55 to extended Heisenberg XXZ models56 and extended Fermi–Hubbard models57 in optical lattices.
Methods
Preparing a density-matched degenerate Bose–Fermi mixture
23Na atoms and 40K atoms were loaded into a three-dimensional magneto-optical trap (MOT) from a Zeeman-slower stage for 23Na and a 2D-MOT stage for 40K, followed by grey-molasses cooling for Na atoms on the D1 line. Both species were transferred into an optically plugged magnetic quadropole trap and cooled by forced radiofrequency evaporation. After evaporation, there were 1.6 × 108 Na atoms and 1.0 × 106 K atoms at a temperature of 6 μK, of which 2 × 107 Na atoms and 6 × 105 K atoms were loaded into an optical trap that transported the mixture from the MOT chamber to a glass cell. This transport trap was formed by two 1,064-nm laser beams intersecting at an angle of 3° to increase axial confinement58. After the transport, the mixture was transferred into a crossed optical dipole trap formed by one of the transport beams and an additional 1,550-nm beam (1,550/1,064-nm trap; Fig. 1a). The waists of these two beams in the vertical and horizontal directions were 50 × 100 μm and 50 × 150 μm, respectively. Optical evaporation was performed by exponentially ramping down the beam powers. During the evaporation, a trap formed by two 785-nm beams with waists of 30 × 400 μm and 50 × 50 μm (785-nm trap; Extended Data Fig. 1b) was ramped on. The wavelength of this trap was chosen such that it was closely detuned from the D lines of the K atoms, and the polarizabilities of the Feshbach and ground-state molecules were equal59. After evaporation, the K atoms underwent two Landau–Zener sweeps for a hyperfine transfer from \({\left\vert F,\,{m}_{\rm{F}}\right\rangle }={\left\vert 9/2,\,9/2\right\rangle}\) to \({\left\vert 9/2,\,-9/2\right\rangle}\), where F is the total atomic angular momentum and mF is its projection onto the axis of the magnetic field. The Na atoms remained in \({\left\vert 1,\,1\right\rangle}\). The first state transfer from \({\left\vert 9/2,\,9/2\right\rangle}\) to \({\left\vert 9/2,\,-7/2\right\rangle}\) was performed at a magnetic field of 74 G, and the second state transfer from \({\left\vert 9/2,\,-7/2\right\rangle}\) to \({\left\vert 9/2,\,-9/2\right\rangle}\) was performed at 81 G. The magnetic fields were chosen to minimize changes in the interspecies interaction during the sweeps. After the state preparation, we turned on a magnetic field gradient of 6.4 G cm−1 to levitate the Na atoms and K atoms against gravity. Afterwards, the 1,550/1,064-nm trap was ramped down, decompressing mainly the Na atoms and leading to a trap configuration dominated by the 785-nm beams. In this trap configuration, the trap frequencies of the K atoms were approximately three times larger than those of the Na atoms. For the measurements described in the main text, the trapping frequencies in the (x, y, z)-direction were 2π × (72, 90, 187) Hz and 2π × (23, 28, 61) Hz for the K atoms and Na atoms, respectively. This procedure led to the preparation of a density-matched mixture of 2.3 × 105 40K atoms at T = 80 nK (corresponding to T/TF ≈ 0.2 where TF is the Fermi temperature), and a BEC of 0.8 × 105 23Na atoms with a condensate fraction of ~60%. In the measurements of the QPT, where we start the association from 1.8 × 105 K atoms, the Fermi wavevector is given by kF = 2π × (1.5 × 106) m−1.
Feshbach association and preparation for ground-state transfer
To associate Feshbach molecules, we used a series of magnetic-field ramps (Extended Data Fig. 1b). First, the magnetic field was quickly ramped to 78.6 G, followed by the association ramp across the Feshbach resonance at 78.3 G with a ramp speed of 3.5 G ms−1. This slower ramp stopped at 77.8 G, where the formation of Feshbach molecules saturated. To minimize the loss of the Feshbach molecules, we subsequently ramped the magnetic field quickly to 75 G. At this magnetic field, the magnetic moment of the Feshbach molecules reduced by a factor of six compared to the open-channel-dominated Feshbach molecules close to the resonance. We compensated the reduced magnetic moment by increasing the magnetic-field gradient to 40 G cm−1 in ~200 μs. This levitated the Feshbach molecules against gravity and, in addition, removed unassociated atoms from the trap due to their larger magnetic moment.
Imperfect timing of the magnetic-field and magnetic-field-gradient ramps resulted in a temporary tilt of the trap, which induced collective oscillations of the molecular cloud. We minimized the collective oscillations by carefully programming the magnetic field and subsequently the magnetic force on the molecules over the course of ~25 ms once the magnetic-field gradient had reached 40 G cm−1 (Extended Data Fig. 1c). Once the collective oscillations stopped, the 1,550/1,064-nm trap was compressed within 30 ms. Because the trap was deep enough to hold the molecules without magnetic-field levitation, the magnetic-field gradient was ramped down within 30 ms and the magnetic field was ramped to 72.3 G, where the magnetic moment of the Feshbach molecules vanished. Finally, the stimulated Raman adiabatic passage scheme was used, as described in ref. 4.
Feshbach association at 1,550/1,064 nm
As a comparison to the species-dependent 785-nm trap, we characterized the association of Feshbach molecules in our typical 1,550/1,064-nm trap, where the densities are strongly mismatched as shown in Fig. 1c. The measurement started with 2.9 × 105 K atoms and 1.4 × 105 Na atoms, where the condensed fraction of Na atoms was ~60%. In contrast to the measurements described above, the ramp speed of the magnetic field across the Feshbach resonance was changed to 2.4 G ms−1 to maximize the number of Feshbach molecules. The association ramp through the Feshbach resonance was stopped at different magnetic fields, followed by a magnetic-field jump to 72.3 G for Stern–Gerlach detection. Extended Data Fig. 2 shows that only 30,000 Feshbach molecules were associated, resulting in an association efficiency of less than 25%. Around 60% of the Na atoms, primarily Na atoms in the BEC, have been lost due to interspecies collisions. This observation is in contrast to the measurements in the 785-nm trap, where at most 10% of the Na atoms were lost.
Immiscibility and collapse in Bose–Fermi mixtures
Theory17,31,60,61 and early experiments62,63 suggest that, for strong interactions, especially close to unitarity, the Bose–Fermi mixture might undergo collapse. However, the timescale for the collapse to occur is on the order of the trapping period. In our experiment, we ramped through the strongly interacting regime on a timescale shorter than the trapping period, prohibiting the collapse to occur. Indeed, our observations show that the Bose–Fermi mixture remains in a metastable state on such experimental timescales, which in turn allows us to explore the physics of the phase diagram shown in Fig. 1a. Specifically, the density increase in a collapse scenario would lead to enhanced interspecies loss, which we do not observe. As a further instability one might also consider immiscibility of the mixture leading to a separation of bosonic and fermionic atoms. Such immiscibility is expected to occur for repulsive interactions between bosons and fermions. We are, however, following the attractive interaction branch of the system and, given the efficient molecule formation we observe, immiscibility, which would be characterized by poor spatial overlap, can be excluded.
Ramp speed of the Feshbach association
We measured the depletion of the condensate fraction as a function of \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) at three different ramp speeds. As shown in Extended Data Fig. 3, the depletion of the condensate coincides for ramp speeds of 1.7 G ms−1 and 3.5 G ms−1 while showing a shift towards higher \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) for ramp speeds of 9 G ms−1. We attribute the higher residual condensate fraction for the data shown by points to an imperfect trap alignment, which leads to a worse density matching between bosons and fermions.
Heating during the phase transition
We measured the heating of the bosons as a function of \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) at a ramp speed of 3.5 G ms−1 by extracting the temperature from the thermal wings of the bosons. As shown in Extended Data Fig. 4, the heating starts around \({{({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\approx 0.8}\), where the system is close to the predicted transition point. This agrees with the expectation that the system is excited when the response time of the system becomes slow near the critical point. Interestingly, the heating is mainly in the horizontal direction, along which the confinement is much weaker than along the vertical direction. The anisotropy of the heating and the directional depletion of the BEC (Fig. 2a) indicate involved dynamics of the strongly interacting mixture, which may result from the varying density ratio within the trap and the associated inward movement of the phase boundary. Thus, the quantity deduced from time-of-flight distributions should be regarded rather as an average kinetic energy of the particles, an effective temperature, rather than the actual temperature of the sample. In future work, it would be interesting to resolve the dynamics of the mixture close to the critical point, preferably in a set-up where homogeneous samples can be realized (for example, in a box trap) and high-resolution imaging is available for local detection.
We note that the temperature of the bosons is lower than the global temperature of the fermions (80 nK). We attribute the temperature difference to the reduced interspecies heat contact during the sympathetic cooling once the bosons condense. However, the region of interest where the phase transition takes place is mainly inside the BEC (the centre of the Fermi cloud). In this region the local condensate density is much higher than that of the thermal bosons (Fig. 1b), and the fermions are deeply degenerate, that is, with very few particle–hole excitations compared to the Fermi surface. Therefore our system can be described by an effective local temperature close to zero.
Comparison of NSCT and fRG calculations
The NSCT approach, from which we obtain the condensate depletion at equal density, predicts the polaron-to-molecule transition to occur at \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}={1.60}\) (ref. 18). For finite boson densities it predicts the phase transition between the polaronic condensate and the molecular phase to take place beyond this value as the boson concentration increases, that is, \({{({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1} > 1.60}\). Specifically, for the case of balanced densities, nB = nF, it predicts \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}={2.02}\).
The NSCT approach, however, only takes into account single particle–hole excitations of the Fermi sea64 and underestimates the modification of the binding energy of molecules inside the many-body environment. Indeed, when applying the NSCT approach18 to the Fermi–polaron problem at mass balance, one finds the polaron-to-molecule transition to occur at \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}={1.27}\) (ref. 65), while techniques that include higher-order correlations such as fRG36 and state-of-the-art diagramatic Monte Carlo (QMC)66,67 predict a value of \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}^{-1}={0.90}\).
Thus, to obtain a more accurate description of the critical interaction strength for the heteronuclear case considered in this work, we used a fRG scheme, which takes into account an infinite number of particle–hole excitations in the Fermi sea36. The resulting polaron and molecule energies are shown in Fig. 1e, yielding a polaron-to-molecule transition at \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}={1.16}\). As shown in Fig. 1d, we find that the polaron quasiparticle weight obtained in the impurity limit already describes the condensate fraction well, except for its discontinuity at the polaron-to-molecule transition. From investigations of two-component Fermi gases, it is expected that this discontinuity will be smoothed out due to the finite boson density, temperature or combinations thereof27,37. Moreover, as explicitly shown in refs. 18,19,27,37 and suggested by mean-field arguments19, one expects the transition to shift to larger values of \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) as the boson density increases. Hence, the value of \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}={1.16}\) obtained from the fRG in the impurity limit can be regarded as a lower bound on the actual location of the QPT at \({({k}_{\rm{F}}{a}_{\rm{BF}})}_{\rm{c}}\).
We note that the polaron and molecule energies cross at a rather shallow angle (Fig. 1e). As a result, the underestimation of the molecule energy is the main reason for the difference in the predicted location of the polaron-to-molecule transition in the NSCT and fRG calculations. The quasiparticle weight is, in contrast, less affected, and, as shown in Extended Data Fig. 5, both approaches yield similar results for the quasiparticle weight of a bosonic impurity. Based on this finding, NSCT theory can also be expected to give a reliable prediction for the condensate fraction at finite boson density18.
Projection of polaronic states onto deeply bound molecules
As is evident from Fig. 2b, we detect a finite number of Feshbach molecules even before the phase transition. This can be understood from the fact that the rapid ramp to 72.3 G projects the system onto deeply bound molecules. As a result, short-distance pairing correlations between bosons and fermions are effectively measured before the phase transition. However, once the phase transition is crossed in the initial magnetic-field ramp, all bosons are bound into weakly bound molecules in an adiabatic fashion. In that case, the weakly bound Feshbach molecules are transferred into deeply bound states by the subsequent rapid magnetic-field ramp.
Here we demonstrate that a simple Fermi–polaron wavefunction indeed overlaps with deeply bound molecules when a projection measurement, as described in the main text, is performed. Similar to the calculations performed in ref. 68, we define the molecule number operator as
Here, dq and cq are the fermionic and bosonic annihilation operators, respectively, and ϕp(k) denotes the wavefunction of the molecule in vacuum at centre-of-mass momentum p. We approximate it with the form valid for an attractive contact interaction potential:
Here, Eb denotes the energy of the molecule at p = 0, m denotes the mass of the fermions, and α is given by the ratio of the bosonic and the fermionic mass.
The operator \({\hat{N}}_{{{\rm{Mol}}}}\) measures the number of projected molecules with respect to the Chevy Ansatz69 for the Fermi polaron
as \({N}_{{{\rm{Mol}}}}={\left\langle \,{{\rm{Pol}}}\,\right\vert {\hat{N}}_{{{\rm{Mol}}}}\left\vert \,{{\rm{Pol}}}\,\right\rangle}\). Here, α0 and αkq denote variational parameters and \({\left\vert \,{{{{\rm{FS}}(N)}}}\,\right\rangle}\) denotes a Fermi sea containing N fermions.
The resulting fractions are shown in Extended Data Fig. 6 for a mass ratio of α = 23/40 and different values of Eb. For the binding energies shown, it can be seen that with increasing \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\), the molecule fraction increases, with the fraction becoming smaller as Eb increases. This shows that, although the polaron is by no means a molecular state, it still features pairing correlations that will lead to a finite overlap with deeply bound molecules. Note that when the transition to the molecular phase is reached, in our experimental procedure the associated weakly bound molecules will be transferred nearly adiabatically to the more deeply bound molecules approximately described by equation (2). Accordingly, the number of observed molecules would approximately saturate (in the absence of losses). However, because, during the final part of the initial ramp, excess bosons undergo lossy collisions with the molecules, the number of molecules will be further reduced and it is thus expected that the number of observed molecules will in fact be maximized at the transition using our experimental procedure.
Two-body loss of Feshbach and ground-state molecules
We measured the two-body loss rate of Feshbach and ground-state molecules. For Feshbach molecules, the loss measurement was performed after the 100-ms holding time, during which collective oscillations are dampened out and the 1,550/1,064-nm trap has been compressed. The loss measurement of ground-state molecules was performed immediately after the transfer into the ground state, followed by a removal of the residual Feshbach molecules by resonant light pulses. The trapping frequency for Feshbach and ground-state molecules was (ωx, ωy, ωz) = 2π × (71, 99, 234) Hz, because we increased the power of the 1,550/1,064-nm trap to compensate for the change of polarizabilities between the Feshbach and ground-state molecules.
We started from a density-dependent two-body loss model with heating:
where n represents the average density and T the temperature of the molecular sample. The two-body loss coefficient is expected to scale linearly with temperature, as was experimentally confirmed for fermionic ground-state molecules70,71. With this knowledge, we defined the temperature-independent loss coefficient b = β/T, where we obtain the temperature T by fitting Fermi–Dirac distribution to the molecular clouds. In a first step, we fitted the temperature with a linear-heating model Tlin(t) = T0 + ht, where T0 is the initial temperature and h the heating rate. Using this linear model for heating, we solve equation (5) and obtain9
where n0 describes the initial density of the sample. We fit equation (6) to our data with n0 and b as free parameters. In analogy to ref. 9, we extracted the density of the sample by approximating the degenerate Fermi gas as a classical gas at a temperature of Tcl. We obtain Tcl by fitting a Gaussian distribution to the time-of-flight images. The average in situ density of the classical gas is given by
where \({\bar{\omega }}\) is the geometric average of the trapping frequency, and the classical temperature Tcl accounts for the Fermi pressure as well as the kinetic energy of the sample, thus overestimating the actual temperature. Still, this effective model allows us to determine the density of the sample, even in the degenerate regime, with the least assumptions with respect to the loss and whether the sample is in thermal equilibrium. The accuracy in determining the density for degenerate Fermi samples using a Gaussian distribution instead of a Fermi–Dirac distribution was checked numerically in ref. 72. This shows that the error is negligible for Fermi gases at temperatures as low as 0.2TF.
Extended Data Fig. 7 shows the loss measurement of the Feshbach and ground-state molecules. For Feshbach molecules we get bFB = 3.8(5) × 10−12 cm3 μK−1 s−1 and for ground-state molecules we get bGS = 4.8(6) × 10−11 cm3 μK−1 s−1.
Error bars for the measurements
The error bars in \({({k}_{\rm{F}}{a}_{\rm{BF}})}^{-1}\) in Figs. 1d and 2 result from the magnetic field uncertainty of 15 mG and an error of 10% in the average trapping frequency. The vertical error bars in Figs. 1d and 2, as well as Extended Data Figs. 2, 3 and 6, are the standard deviation of three to five measurements.
Data availability
The experimental data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
All relevant codes are available from the corresponding author upon reasonable request.
References
Chin, C., Grimm, R., Julienne, P. & Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 82, 1225–1286 (2010).
Sidler, M. et al. Fermi polaron-polaritons in charge-tunable atomically thin semiconductors. Nat. Phys. 13, 255–261 (2017).
Ni, K.-K. et al. A high phase-space-density gas of polar molecules. Science 322, 231–235 (2008).
Park, J. W., Will, S. A. & Zwierlein, M. W. Ultracold dipolar gas of fermionic 23Na40K molecules in their absolute ground state. Phys. Rev. Lett. 114, 205302 (2015).
Rvachov, T. M. et al. Long-lived ultracold molecules with electric and magnetic dipole moments. Phys. Rev. Lett. 119, 143001 (2017).
Seeßelberg, F. et al. Modeling the adiabatic creation of ultracold polar 23Na40K molecules. Phys. Rev. A 97, 013405 (2018).
Yang, H. et al. Observation of magnetically tunable Feshbach resonances in ultracold 23Na40K + 40K collisions. Science 363, 261–264 (2019).
Mak, K. F. et al. Tightly bound trions in monolayer MoS2. Nat. Mater. 12, 207–211 (2013).
De Marco, L. et al. A degenerate Fermi gas of polar molecules. Science 363, 853–856 (2019).
Enss, T. & Zwerger, W. Superfluidity near phase separation in Bose–Fermi mixtures. Eur. Phys. J. B 68, 383–389 (2009).
Matuszewski, M., Taylor, T. & Kavokin, A. V. Exciton supersolidity in hybrid Bose–Fermi systems. Phys. Rev. Lett. 108, 060401 (2012).
Shelykh, I. A., Taylor, T. & Kavokin, A. V. Rotons in a hybrid Bose–Fermi system. Phys. Rev. Lett. 105, 140402 (2010).
Cotleţ, O., Zeytinoğlu, S., Sigrist, M., Demler, E. & Imamoğlu, A. Superconductivity and other collective phenomena in a hybrid Bose–Fermi mixture formed by a polariton condensate and an electron system in two dimensions. Phys. Rev. B 93, 054510 (2016).
Powell, S., Sachdev, S. & Büchler, H. P. Depletion of the Bose–Einstein condensate in Bose–Fermi mixtures. Phys. Rev. B 72, 024534 (2005).
Suzuki, K., Miyakawa, T. & Suzuki, T. p-wave superfluid and phase separation in atomic Bose–Fermi mixtures. Phys. Rev. A 77, 043629 (2008).
Fratini, E. & Pieri, P. Pairing and condensation in a resonant Bose–Fermi mixture. Phys. Rev. A 81, 051605 (2010).
Ludwig, D., Floerchinger, S., Moroz, S. & Wetterich, C. Quantum phase transition in Bose–Fermi mixtures. Phys. Rev. A 84, 033629 (2011).
Guidini, A., Bertaina, G., Galli, D. E. & Pieri, P. Condensed phase of Bose–Fermi mixtures with a pairing interaction. Phys. Rev. A 91, 023603 (2015).
von Milczewski, J., Rose, F. & Schmidt, R. Functional-renormalization-group approach to strongly coupled Bose–Fermi mixtures in two dimensions. Phys. Rev. A 105, 013317 (2022).
Kinnunen, J. J., Wu, Z. & Bruun, G. M. Induced p-wave pairing in Bose–Fermi mixtures. Phys. Rev. Lett. 121, 253402 (2018).
Laussy, F. P., Kavokin, A. V. & Shelykh, I. A. Exciton-polariton mediated superconductivity. Phys. Rev. Lett. 104, 106402 (2010).
Hu, M.-G. et al. Bose polarons in the strongly interacting regime. Phys. Rev. Lett. 117, 055301 (2016).
Jørgensen, N. B. et al. Observation of attractive and repulsive polarons in a Bose–Einstein condensate. Phys. Rev. Lett. 117, 055302 (2016).
Yan, Z. Z., Ni, Y., Robens, C. & Zwierlein, M. W. Bose polarons near quantum criticality. Science 368, 190–194 (2020).
Schirotzek, A., Wu, C.-H., Sommer, A. & Zwierlein, M. W. Observation of Fermi polarons in a tunable Fermi liquid of ultracold atoms. Phys. Rev. Lett. 102, 230402 (2009).
Koschorreck, M. et al. Attractive and repulsive Fermi polarons in two dimensions. Nature 485, 619–622 (2012).
Ness, G. et al. Observation of a smooth polaron-molecule transition in a degenerate Fermi gas. Phys. Rev. X 10, 041019 (2020).
Fritsche, I. et al. Stability and breakdown of Fermi polarons in a strongly interacting Fermi–Bose mixture. Phys. Rev. A 103, 053314 (2021).
Carr, L. D., DeMille, D., Krems, R. V. & Ye, J. Cold and ultracold molecules: science, technology and applications. New J. Phys. 11, 055049 (2009).
Bohn, J. L., Rey, A. M. & Ye, J. Cold molecules: progress in quantum engineering of chemistry and quantum matter. Science 357, 1002–1010 (2017).
Marchetti, F. M., Mathy, C. J. M., Huse, D. A. & Parish, M. M. Phase separation and collapse in Bose–Fermi mixtures with a Feshbach resonance. Phys. Rev. B 78, 134517 (2008).
Bertaina, G., Fratini, E., Giorgini, S. & Pieri, P. Quantum Monte Carlo study of a resonant Bose–Fermi mixture. Phys. Rev. Lett. 110, 115303 (2013).
Zwerger, W. The BCS-BEC Crossover and the Unitary Fermi Gas Vol. 836 (Springer, 2011).
Haussmann, R., Rantner, W., Cerrito, S. & Zwerger, W. Thermodynamics of the BCS-BEC crossover. Phys. Rev. A 75, 023610 (2007).
Houcke, K. V. et al. Feynman diagrams versus Fermi-gas Feynman emulator. Nat. Phys. 8, 366–370 (2012).
Schmidt, R. & Enss, T. Excitation spectra and RF response near the polaron-to-molecule transition from the functional renormalization group. Phys. Rev. A 83, 063620 (2011).
Parish, M. M., Adlong, H. S., Liu, W. E. & Levinsen, J. Thermodynamic signatures of the polaron-molecule transition in a Fermi gas. Phys. Rev. A 103, 023312 (2021).
Viel, A. & Simoni, A. Feshbach resonances and weakly bound molecular states of boson–boson and boson–fermion NaK pairs. Phys. Rev. A 93, 042701 (2016).
Chen, X.-Y. et al. Suppression of unitary three-body loss in a degenerate Bose–Fermi mixture. Phys. Rev. Lett. 128, 153401 (2022).
Bloom, R. S., Hu, M.-G., Cumby, T. D. & Jin, D. S. Tests of universal three-body physics in an ultracold Bose–Fermi mixture. Phys. Rev. Lett. 111, 105301 (2013).
Bause, R. et al. Efficient conversion of closed-channel-dominated feshbach molecules of 23Na40K to their absolute ground state. Phys. Rev. A 104, 043321 (2021).
Tobias, W. G. Thermalization and sub-Poissonian density fluctuations in a degenerate molecular Fermi gas. Phys. Rev. Lett. 124, 033401 (2020).
Zhang, Z., Chen, L., Yao, K.-X. & Chin, C. Transition from an atomic to a molecular Bose–Einstein condensate. Nature 592, 708–711 (2021).
Witczak-Krempa, W., Sørensen, E. S. & Sachdev, S. The dynamics of quantum criticality revealed by quantum Monte Carlo and holography. Nat. Phys. 10, 361–366 (2014).
Takekoshi, T. et al. Ultracold dense samples of dipolar RbCs molecules in the rovibrational and hyperfine ground state. Phys. Rev. Lett. 113, 205301 (2014).
Molony, P. K. et al. Creation of ultracold 87Rb133Cs molecules in the rovibrational ground state. Phys. Rev. Lett. 113, 255301 (2014).
Guo, M. et al. Creation of an ultracold gas of ground-state dipolar 23Na87Rb molecules. Phys. Rev. Lett. 116, 205303 (2016).
Voges, K. K. et al. Ultracold gas of bosonic 23Na39K ground-state molecules. Phys. Rev. Lett. 125, 083401 (2020).
Cairncross, W. B. et al. Assembly of a rovibrational ground state molecule in an optical tweezer. Phys. Rev. Lett. 126, 123402 (2021).
Warner, C. et al. Overlapping Bose–Einstein condensates of 23Na and 133Cs. Phys. Rev. A 104, 033302 (2021).
Valtolina, G. et al. Dipolar evaporation of reactive molecules to below the Fermi temperature. Nature 588, 239–243 (2020).
Li, J.-R. et al. Tuning of dipolar interactions and evaporative cooling in a three-dimensional molecular quantum gas. Nat. Phys. 17, 1144–1148 (2021).
Schindewolf, A. et al. Evaporation of microwave-shielded polar molecules to quantum degeneracy. Nature 607, 677–681 (2022).
Baranov, M. A., Dalmonte, M., Pupillo, G. & Zoller, P. Condensed matter theory of dipolar quantum gases. Chem. Rev. 112, 5012–5061 (2012).
Veljić, V., Pelster, A. & Balaž, A. Stability of quantum degenerate Fermi gases of tilted polar molecules. Phys. Rev. Res. 1, 012009 (2019).
Peter, D., Müller, S., Wessel, S. & Büchler, H. P. Anomalous behavior of spin systems with dipolar interactions. Phys. Rev. Lett. 109, 025303 (2012).
Gadsbølle, A.-L. & Bruun, G. M. Dipolar fermions in a two-dimensional lattice at nonzero temperature. Phys. Rev. A 86, 033623 (2012).
Gross, C., Gan, H. C. J. & Dieckmann, K. All-optical production and transport of a large 6Li quantum gas in a crossed optical dipole trap. Phys. Rev. A 93, 053424 (2016).
Vexiau, R. et al. Dynamic dipole polarizabilities of heteronuclear alkali dimers: optical response, trapping and control of ultracold molecules. Int. Rev. Phys. Chem. 36, 709–750 (2017).
Mølmer, K. Bose condensates and Fermi gases at zero temperature. Phys. Rev. Lett. 80, 1804–1807 (1998).
Yu, Z.-Q., Zhang, S. & Zhai, H. Stability condition of a strongly interacting boson–fermion mixture across an interspecies Feshbach resonance. Phys. Rev. A 83, 041603 (2011).
Zaccanti, M. et al. Control of the interaction in a Fermi–Bose mixture. Phys. Rev. A 74, 041605 (2006).
Ospelkaus, C., Ospelkaus, S., Sengstock, K. & Bongs, K. Interaction-driven dynamics of 40K−87Rb fermion–boson gas mixtures in the large-particle-number limit. Phys. Rev. Lett. 96, 020401 (2006).
Lobo, C., Recati, A., Giorgini, S. & Stringari, S. Normal state of a polarized Fermi gas at unitarity. Phys. Rev. Lett. 97, 200403 (2006).
Punk, M., Dumitrescu, P. T. & Zwerger, W. Polaron-to-molecule transition in a strongly imbalanced Fermi gas. Phys. Rev. A 80, 053605 (2009).
Prokof’ev, N. & Svistunov, B. Fermi-polaron problem: diagrammatic Monte Carlo method for divergent sign-alternating series. Phys. Rev. B 77, 020408 (2008).
Prokof’ev, N. V. & Svistunov, B. V. Bold diagrammatic Monte Carlo: a generic sign-problem tolerant technique for polaron models and possibly interacting many-body problems. Phys. Rev. B 77, 125101 (2008).
Pini, M., Pieri, P., Jäger, M., Denschlag, J. H. & Strinati, G. C. Pair correlations in the normal phase of an attractive Fermi gas. New J. Phys. 22, 083008 (2020).
Chevy, F. Universal phase diagram of a strongly interacting Fermi gas with unbalanced spin populations. Phys. Rev. A 74, 063628 (2006).
Ospelkaus, S. et al. Quantum-state controlled chemical reactions of ultracold potassium-rubidium molecules. Science 327, 853–857 (2010).
Bause, R. et al. Collisions of ultracold molecules in bright and dark optical dipole traps. Phys. Rev. Res. 3, 033013 (2021).
DeMarco, B. Quantum Behavior of an Atomic Fermi Gas. PhD thesis, Univ. Colorado (2001).
Acknowledgements
We thank P. Pieri for stimulating discussions and providing calculations of the condensate fraction for an equal-density mixture, T. Shi for stimulating discussions, and X. Li and T. Hilker for insightful comments on our paper. We thank the previous members of the MPQ NaK Lab, especially C. Gohle, for their contributions to the experimental apparatus. We acknowledge funding support by the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy – EXC-2111 – 390814868 (the Munich Center for Quantum Science and Technology) and under grant no. FOR 2247. The experimental team acknowledges support from the Max Planck Society and the European Union (PASQuanS grant no. 817482). R.S. acknowledges funding by the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy – EXC-2181/1-390900948 (the Heidelberg STRUCTURES Excellence Cluster). J.v.M. is supported by a fellowship of the International Max Planck Research School for Quantum Science and Technology (IMPRS-QST). A.S. acknowledges funding from the Max Planck Harvard Research Center for Quantum Optics.
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
All authors contributed substantially to the work presented in this paper. M.D. and X.-Y.C. carried out the experiments and, together with A.S. and R.B., they maintained and improved the experimental set-up. M.D. analysed the data. J.v.M. and R.S. performed the theoretical calculations. R.S., I.B. and X.-Y.L. supervised the study. All authors worked on interpretation of the data and contributed to the final paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Pietro Massignan and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Trap configurations and sequence for molecule association.
a, Trap configuration of the 1550/1064-nm trap and b, the 785-nm trap. The magnetic field and its gradient are along the vertical direction (z-direction). c, Typical timing sequence for the association of ground-state molecules showing ramps of the magnetic field (red), its gradient (blue) and the power of the 1550/1064-nm trap (gray). I. Association of Feshbach molecules by three-staged magnetic field ramp. II. Removal of unassociated atoms. III. Compression of the 1550/1064-nm trap while the power of the 785-nm trap remains unchanged. IV. Removal of the levitation gradient for subsequent STIRAP pulses. The black vertical solid and dashed lines separate different stages of the sequence. The horizontal gray dashed line marks the Feshbach resonance at 78.3 G.
Extended Data Fig. 2 Feshbach association in the (a) 1550/1064-nm and (b) 785-nm trap.
Number of Feshbach molecules (gray) and the sum of associated and unassociated sodium atoms (orange).
Extended Data Fig. 3 Feshbach association at various ramp speeds.
Order parameter ϕ as a function of \({({k}_{F}{a}_{BF})}^{-1}\) at ramp speeds of 1.7 G/ms (red points), 3.5 G/ms (orange points) and 9 G/ms (blue points). In addition, we show the data from the main text at the ramp speed of 3.5 G/ms for \({\tilde{n}}_{B}/{\tilde{n}}_{F}=1.3\) (grey diamonds).
Extended Data Fig. 4 Effective temperature of the bosons extracted from the thermal wings as a function of the interaction strength in the vertical (dark gray) and horizontal direction (light gray).
The predicted polaron-to-molecule according to the fRG calculation at \({({k}_{F}{a}_{BF})}^{-1}=1.16\) is indicated by the red dashed line.
Extended Data Fig. 5 Impurity quasiparticle weight in the Fermi polaron problem for α = 23/40.
The quasiparticle weight of the impurity as a function of the interaction strength is shown as obtained from the fRG (red, solid) and the NSCT approach (black, dashed). While both methods yield similar results they differ in the prediction of the point where the polaron-to-molecule transitions occurs, beyond which the occupied quasiparticle weight drops to zero. To indicate the effect of finite boson density, the condensate fraction of the mixture computed in NSCT is shown for nB = nF (black solid, also shown in Fig. 1d).
Extended Data Fig. 6 Number of projected molecules.
The projected molecule fraction NMol obtained from the Fermi polaron state within the Chevy Ansatz69 is shown as a function of the interaction parameter \({({k}_{F}{a}_{BF})}^{-1}\) for different binding energies of the deeply bound molecule.
Extended Data Fig. 7 Lifetime of NaK* Feshbach (left panel) and NaK ground-state molecules (right panel).
The upper panel figure shows the average density n of the Feshbach molecules (gray points) and ground-state molecules (purple points) as a function of holding time. The data is fitted with Eq. (6). The result of the fits are plotted as solid lines. The error bars are statistical errors derived from the atom number fluctuations. For the fitting procedure we only consider data points where the molecule number is larger than 1 × 104. The lower panel shows the temperature of the Feshbach molecules (gray points) and the ground-state molecules (purple points) as a function of the holding time extracted from Fermi-Dirac distribution fits. The dashed lines represent the linear fit of the temperature.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Duda, M., Chen, XY., Schindewolf, A. et al. Transition from a polaronic condensate to a degenerate Fermi gas of heteronuclear molecules. Nat. Phys. 19, 720–725 (2023). https://doi.org/10.1038/s41567-023-01948-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-023-01948-1
This article is cited by
-
Observation of Bose–Einstein condensation of dipolar molecules
Nature (2024)
-
Ultracold field-linked tetratomic molecules
Nature (2024)
-
Mediated interactions between Fermi polarons and the role of impurity quantum statistics
Nature Physics (2024)
-
Quantum state manipulation and cooling of ultracold molecules
Nature Physics (2024)
-
Intersections of ultracold atomic polarons and nuclear clusters: how is a chart of nuclides modified in dilute neutron matter?
AAPPS Bulletin (2024)