Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Many-body Hilbert space scarring on a superconducting processor

Nature Physics volume 19, pages 120–125 (2023)Cite this article

Subjects

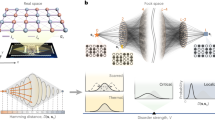
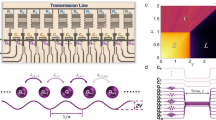
Abstract

Quantum many-body scarring (QMBS) is a recently discovered form of weak ergodicity breaking in strongly interacting quantum systems, which presents opportunities for mitigating thermalization-induced decoherence in quantum information processing applications. However, the existing experimental realizations of QMBS are based on systems with specific kinetic constrains. Here we experimentally realize a distinct kind of QMBS by approximately decoupling a part of the many-body Hilbert space in the computational basis. Utilizing a programmable superconducting processor with 30 qubits and tunable couplings, we realize Hilbert space scarring in a non-constrained model in different geometries, including a linear chain and quasi-one-dimensional comb geometry. By reconstructing the full quantum state through quantum state tomography on four-qubit subsystems, we provide strong evidence for QMBS states by measuring qubit population dynamics, quantum fidelity and entanglement entropy after a quench from initial unentangled states. Our experimental findings broaden the realm of scarring mechanisms and identify correlations in QMBS states for quantum technology applications.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Experimental setup and identification of QMBS states via quantum state tomography.
Fig. 2: Experimentally observed qubit dynamics.
Fig. 3: Scaling behaviour.
Fig. 4: QMBS states in a comb tensor system.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available at https://doi.org/10.5518/1204.

Code availability

All the relevant source codes are available from the corresponding authors upon reasonable request.

References

  1. Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).

    Article  ADS  Google Scholar 

  2. Georgescu, I. M., Ashhab, S. & Nori, F. Quantum simulation. Rev. Mod. Phys. 86, 153–185 (2014).

    Article  ADS  Google Scholar 

  3. Mi, X. et al. Information scrambling in computationally complex quantum circuits. Science 374, 1479–1483 (2021).

    Article  ADS  Google Scholar 

  4. Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).

    Article  ADS  Google Scholar 

  5. Swingle, B., Bentsen, G., Schleier-Smith, M. & Hayden, P. Measuring the scrambling of quantum information. Phys. Rev. A 94, 040302 (2016).

    Article  ADS  Google Scholar 

  6. Xu, K. et al. Emulating many-body localization with a superconducting quantum processor. Phys. Rev. Lett. 120, 050507 (2018).

    Article  ADS  Google Scholar 

  7. Landsman, K. A. et al. Verified quantum information scrambling. Nature 567, 61–65 (2019).

    Article  ADS  Google Scholar 

  8. Morong, W. et al. Observation of Stark many-body localization without disorder. Nature 599, 393–398 (2021).

    Article  ADS  Google Scholar 

  9. Deutsch, J. M. Quantum statistical mechanics in a closed system. Phys. Rev. A 43, 2046–2049 (1991).

    Article  ADS  Google Scholar 

  10. Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 50, 888–901 (1994).

    Article  ADS  Google Scholar 

  11. Rigol, M., Dunjko, V. & Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 452, 854–858 (2008).

    Article  ADS  Google Scholar 

  12. Kaufman, A. M. et al. Quantum thermalization through entanglement in an isolated many-body system. Science 353, 794–800 (2016).

    Article  ADS  Google Scholar 

  13. Bluvstein, D. et al. Controlling quantum many-body dynamics in driven Rydberg atom arrays. Science 371, 1355–1359 (2021).

    Article  ADS  MATH  Google Scholar 

  14. Serbyn, M., Abanin, D. A. & Papić, Z. Quantum many-body scars and weak breaking of ergodicity. Nat. Phys. 17, 675–685 (2021).

    Article  Google Scholar 

  15. Moudgalya, S., Bernevig, B. A. & Regnault, N. Quantum many-body scars and Hilbert space fragmentation: a review of exact results. Rep. Prog. Phys. 85, 086501 (2022).

    Article  ADS  Google Scholar 

  16. Heller, E. J. Bound-state eigenfunctions of classically chaotic Hamiltonian systems: scars of periodic orbits. Phys. Rev. Lett. 53, 1515–1518 (1984).

    Article  ADS  Google Scholar 

  17. Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys. 6, 15–38 (2015).

    Article  ADS  Google Scholar 

  18. Abanin, D. A., Altman, E., Bloch, I. & Serbyn, M. Colloquium: many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 91, 021001 (2019).

    Article  ADS  Google Scholar 

  19. Guo, Q. et al. Stark many-body localization on a superconducting quantum processor. Phys. Rev. Lett. 127, 240502 (2021).

    Article  ADS  Google Scholar 

  20. Guo, Q. et al. Observation of energy-resolved many-body localization. Nat. Phys. 17, 234–239 (2021).

    Article  ADS  Google Scholar 

  21. Omran, A. et al. Generation and manipulation of Schrödinger cat states in Rydberg atom arrays. Science 365, 570–574 (2019).

    Article  ADS  Google Scholar 

  22. Dooley, S. Robust quantum sensing in strongly interacting systems with many-body scars. PRX Quantum 2, 020330 (2021).

    Article  ADS  Google Scholar 

  23. Shiraishi, N. & Mori, T. Systematic construction of counterexamples to the eigenstate thermalization hypothesis. Phys. Rev. Lett. 119, 030601 (2017).

    Article  ADS  Google Scholar 

  24. Moudgalya, S., Regnault, N. & Bernevig, B. A. Entanglement of exact excited states of Affleck-Kennedy-Lieb-Tasaki models: exact results, many-body scars, and violation of the strong eigenstate thermalization hypothesis. Phys. Rev. B 98, 235156 (2018).

    Article  ADS  Google Scholar 

  25. Schecter, M. & Iadecola, T. Weak ergodicity breaking and quantum many-body scars in spin-1 XY magnets. Phys. Rev. Lett. 123, 147201 (2019).

    Article  ADS  Google Scholar 

  26. Moudgalya, S., Bernevig, B. A. & Regnault, N. Quantum many-body scars in a Landau level on a thin torus. Phys. Rev. B 102, 195150 (2020).

    Article  ADS  Google Scholar 

  27. McClarty, P. A., Haque, M., Sen, A. & Richter, J. Disorder-free localization and many-body quantum scars from magnetic frustration. Phys. Rev. B 102, 224303 (2020).

    Article  ADS  Google Scholar 

  28. van Voorden, B., Minář, J. & Schoutens, K. Quantum many-body scars in transverse field Ising ladders and beyond. Phys. Rev. B 101, 220305 (2020).

  29. Hart, O., De Tomasi, G. & Castelnovo, C. From compact localized states to many-body scars in the random quantum comb. Phys. Rev. Res. 2, 043267 (2020).

    Article  Google Scholar 

  30. Zhao, H., Vovrosh, J., Mintert, F. & Knolle, J. Quantum many-body scars in optical lattices. Phys. Rev. Lett. 124, 160604 (2020).

    Article  ADS  Google Scholar 

  31. Kuno, Y., Mizoguchi, T. & Hatsugai, Y. Flat band quantum scar. Phys. Rev. B 102, 241115 (2020).

    Article  ADS  Google Scholar 

  32. O’Dea, N., Burnell, F., Chandran, A. & Khemani, V. From tunnels to towers: quantum scars from Lie algebras and q-deformed Lie algebras. Phys. Rev. Res. 2, 043305 (2020).

    Article  Google Scholar 

  33. Desaules, J.-Y., Hudomal, A., Turner, C. J. & Papić, Z. Proposal for realizing quantum scars in the tilted 1D Fermi-Hubbard model. Phys. Rev. Lett. 126, 210601 (2021).

    Article  ADS  Google Scholar 

  34. Ren, J., Liang, C. & Fang, C. Quasisymmetry groups and many-body scar dynamics. Phys. Rev. Lett. 126, 120604 (2021).

    Article  ADS  Google Scholar 

  35. Fendley, P., Sengupta, K. & Sachdev, S. Competing density-wave orders in a one-dimensional hard-boson model. Phys. Rev. B 69, 075106 (2004).

    Article  ADS  Google Scholar 

  36. Lesanovsky, I. & Katsura, H. Interacting Fibonacci anyons in a Rydberg gas. Phys. Rev. A 86, 041601 (2012).

    Article  ADS  Google Scholar 

  37. Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017).

    Article  ADS  Google Scholar 

  38. Su, G.-X. et al. Observation of unconventional many-body scarring in a quantum simulator. Preprint at https://arxiv.org/abs/2201.00821 (2022).

  39. Jepsen, P. N. et al. Long-lived phantom helix states in Heisenberg quantum magnets. Nat. Phys. 18, 899–904 (2022).

    Article  Google Scholar 

  40. Su, W. P., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698–1701 (1979).

    Article  ADS  Google Scholar 

  41. Wu, Y. et al. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett. 127, 180501 (2021).

    Article  ADS  Google Scholar 

  42. Krantz, P. et al. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 6, 021318 (2019).

    Article  ADS  Google Scholar 

  43. Blais, A., Grimsmo, A. L., Girvin, S. M. & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005 (2021).

    Article  ADS  Google Scholar 

  44. Jafari, R. & Johannesson, H. Loschmidt echo revivals: critical and noncritical. Phys. Rev. Lett. 118, 015701 (2017).

    Article  ADS  Google Scholar 

  45. Najafi, K., Rajabpour, M. A. & Viti, J. Return amplitude after a quantum quench in the XY chain. J. Stat. Mech. 2019, 083102 (2019).

    Article  MATH  Google Scholar 

  46. Maimaiti, W., Andreanov, A., Park, H. C., Gendelman, O. & Flach, S. Compact localized states and flat-band generators in one dimension. Phys. Rev. B 95, 115135 (2017).

    Article  ADS  Google Scholar 

  47. Ho, W. W., Choi, S., Pichler, H. & Lukin, M. D. Periodic orbits, entanglement, and quantum many-body scars in constrained models: matrix product state approach. Phys. Rev. Lett. 122, 040603 (2019).

    Article  ADS  Google Scholar 

  48. Desaules, J.-Y., Pietracaprina, F., Papić, Z., Goold, J. & Pappalardi, S. Extensive multipartite entanglement from SU(2) quantum many-body scars. Phys. Rev. Lett. 129, 020601 (2022).

    Article  ADS  Google Scholar 

  49. Malvania, N. et al. Generalized hydrodynamics in strongly interacting 1D Bose gases. Science 373, 1129–1133 (2021).

    Article  ADS  MATH  Google Scholar 

  50. Neill, C. et al. A blueprint for demonstrating quantum supremacy with superconducting qubits. Science 360, 195–199 (2018).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The device was fabricated at the Micro-Nano Fabrication Center of Zhejiang University. We acknowledge support from the National Natural Science Foundation of China (grant nos. 92065204, U20A2076, 11725419 and 12174342), the National Basic Research Program of China (grant no. 2017YFA0304300) and the Zhejiang Province Key Research and Development Program (grant no. 2020C01019). The work at Arizona State University is supported by AFOSR through grant no. FA9550-21-1-0186. Z.P. and J.Y.D. acknowledge support by EPSRC grants EP/R020612/1 and EP/R513258/1, and by Leverhulme Trust Research Leadership Award RL-2019-015. L.Y. is also supported by the Fundamental Research Funds for the Central Universities.

Author information

Author notes

  1. These authors contributed equally: Pengfei Zhang, Hang Dong, Yu Gao.

Authors and Affiliations

  1. Department of Physics, ZJU-Hangzhou Global Scientific and Technological Innovation Center, Interdisciplinary Center for Quantum Information, and Zhejiang Province Key Laboratory of Quantum Technology and Device, Zhejiang University, Hangzhou, China

    Pengfei Zhang, Hang Dong, Yu Gao, Qiujiang Guo, Jiachen Chen, Jinfeng Deng, Bobo Liu, Wenhui Ren, Yunyan Yao, Xu Zhang, Shibo Xu, Ke Wang, Feitong Jin, Xuhao Zhu, Hekang Li, Chao Song, Zhen Wang, Lei Ying & H. Wang

  2. Institute of Automation, Chinese Academy of Sciences, Beijing, China

    Liangtian Zhao & Jie Hao

  3. School of Physics and Astronomy, University of Leeds, Leeds, UK

    Jean-Yves Desaules & Zlatko Papić

  4. Alibaba-Zhejiang University Joint Research Institute of Frontier Technologies, Hangzhou, China

    Qiujiang Guo, Bing Zhang, Hekang Li, Chao Song, Zhen Wang, Lei Ying & H. Wang

  5. QuEra Computing, Boston, MA, USA

    Fangli Liu

  6. School of Electrical, Computer and Energy Engineering, and Department of Physics, Arizona State University, Tempe, AZ, USA

    Ying-Cheng Lai

Authors
  1. Pengfei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hang Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Liangtian Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jie Hao
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Jean-Yves Desaules
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Qiujiang Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Jiachen Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Jinfeng Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Bobo Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Wenhui Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Yunyan Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Xu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Shibo Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. Ke Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. Feitong Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. Xuhao Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. Bing Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  19. Hekang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  20. Chao Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  21. Zhen Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  22. Fangli Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  23. Zlatko Papić
    View author publications

    You can also search for this author in PubMed Google Scholar

  24. Lei Ying
    View author publications

    You can also search for this author in PubMed Google Scholar

  25. H. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  26. Ying-Cheng Lai
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

L.Y. proposed the idea. L.Y., Y.-C.L., J.Y.D. and Z.P. developed the theory and numerical simulation. P.Z., H.D. and Y.G. performed the experiment, and H.L. and J.C. fabricated the device supervised by H.W. L.Z. and J.H. developed the measurement electronics. L.Y., H.W., Y.-C.L. and Z.P. co-wrote the manuscript. All the authors contributed to the experimental setup, discussions of the results and development of the manuscript.

Corresponding authors

Correspondence to Lei Ying, H. Wang or Ying-Cheng Lai.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Experimental sequence diagram.

Sequence with strongly interacting many-body dynamics, where injecting a π pulse (red wave pulse) serves to lift the two-level qubit from the ground state to the excited state.

Supplementary information

Supplementary Information

Supplementary Figs. 1–20, Tables 1 and 2 and discussion.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, P., Dong, H., Gao, Y. et al. Many-body Hilbert space scarring on a superconducting processor. Nat. Phys. 19, 120–125 (2023). https://doi.org/10.1038/s41567-022-01784-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-022-01784-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing