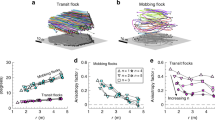
Abstract
Flocking behaviour is often presented as an example of a self-organized process, where individuals continuously negotiate on the direction of travel and compromise by moving along a local average velocity until the group reaches a consensus. Such a collective behaviour does not take advantage of the benefits of hierarchical organizational strategies that confer the leader of the group full control over it with a reduced information flow overhead. Here we study the spontaneous behaviour of small sheep flocks and find that sheep exhibit a collective behaviour that consists of a series of collective motion episodes interrupted by grazing phases. Each motion episode has a temporal leader that guides the group in line formation. Combining experiments and a data-driven model, we provide evidence that group coordination in these episodes results from the propagation of positional information of the temporal leader to all group members through a strongly hierarchical, directed interaction network. Furthermore, we show that group members alternate the role of leader and follower by a random process, which is independent of the navigation mechanism that regulates collective motion episodes. Our analysis suggests that it is possible to conceive intermittent collective strategies that take advantage of both hierarchical and democratic organizational schemes.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The raw data in this work are available in the public repository Zenodo (https://doi.org/10.5281/zenodo.6905807). Data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
Code availability
The custom codes written in Matlab (Matlab 2019a) to analyse the data presented in this paper are available from the corresponding author upon request.
References
Krause, J. & Ruxton, G. D. Living in Groups (Oxford Univ. Press, 2002).
Ioannou, C. C., Guttal, V. & Couzin, I. D. Predatory fish select for coordinated collective motion in virtual prey. Science 337, 1212–1215 (2012).
Berdahl, A., Torney, C. J., Ioannou, C. C., Faria, J. J. & Couzin, I. D. Emergent sensing of complex environments by mobile animal groups. Science 339, 574–576 (2013).
Flack, A., Nagy, M., Fiedler, W., Couzin, I. D. & Wikelski, M. From local collective behavior to global migratory patterns in white storks. Science 360, 911–914 (2018).
Pillot, M.-H., Gautrais, J., Arrufat, P., Couzin, I. D., Bon, R. & Deneubourg, J.-L. Scalable rules for coherent group motion in a gregarious vertebrate. PLoS ONE 6, e14487 (2011).
Strandburg-Peshkin, A., Farine, D. R., Couzin, I. D. & Crofoot, M. C. Shared decision-making drives collective movement in wild baboons. Science 348, 1358–1361 (2015).
Ginelli, F. et al. Intermittent collective dynamics emerge from conflicting imperatives in sheep herds. Proc. Natl Acad. Sci. USA 112, 12729–12734 (2015).
Toulet, S., Gautrais, J., Bon, R. & Peruani, F. Imitation combined with a characteristic stimulus duration results in robust collective decision-making. PLoS ONE 10, e0140188 (2015).
Viscido, S. V., Parrish, J. K. & Grünbaum, D. Individual behavior and emergent properties of fish schools: a comparison of observation and theory. Mar. Ecol. Prog. Ser. 273, 239–249 (2004).
Ballerini, M. et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: evidence from a field study. Proc. Natl Acad. Sci. USA 105, 1232–1237 (2008).
Lukeman, R., Li, Y.-X. & Edelstein-Keshet, L. Inferring individual rules from collective behavior. Proc. Natl Acad. Sci. USA 107, 12576–12580 (2010).
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995).
Couzin, I. D., Krause, J., James, R., Ruxton, G. D. & Franks, N. R. Collective memory and spatial sorting in animal groups. J. Theor. Biol. 218, 1–11 (2002).
Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep. 517, 71–140 (2012).
Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).
Couzin, I. D., Krause, J., Franks, N. R. & Levin, S. A. Effective leadership and decision-making in animal groups on the move. Nature 433, 513–516 (2005).
Guttal, V. & Couzin, I. D. Social interactions, information use and the evolution of collective migration. Proc. Natl Acad. Sci. USA 107, 16172–16177 (2010).
Katz, Y., Tunstrøm, K., Ioannou, C. C., Huepe, C. & Couzin, I. D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl Acad. Sci. USA 108, 18720–18725 (2011).
Herbert-Read, J. E. et al. Inferring the rules of interaction of shoaling fish. Proc. Natl Acad. Sci. USA 108, 18726–18731 (2011).
Nagy, M., Akos, Z., Biro, D. & Vicsek, T. Hierarchical group dynamics in pigeon flocks. Nature 464, 890–893 (2010).
Nagy, M. et al. Context-dependent hierarchies in pigeons. Proc. Natl Acad. Sci. USA 110, 13049–13054 (2013).
Nagy, M., Couzin, I. D., Fiedler, W., Wikelski, M. & Flack, A. Synchronization, coordination and collective sensing during thermalling flight of freely migrating white storks. Philos. Trans. R. Soc. B Biol. Sci. 373, 20170011 (2018).
King, A. J. & Cowlishaw, G. Leaders, followers and group decision-making. Commun. Integr. Biol. 2, 147–150 (2009).
Tyler, S. J. The behaviour and social organization of the new forest ponies. Anim. Behav. Monogr. 5, 87–196 (1972).
Klingel, H. Soziale organisation und verhaltensweisen von Hartmann-und Bergzebras (Equus zebra hartmannae und e. z. zebra). Z. Tierpsychol. 25, 76–88 (1968).
Krueger, K., Flauger, B., Farmer, K. & Hemelrijk, C. Movement initiation in groups of feral horses. Behav. Process. 103, 91–101 (2014).
Portugal, S. J. et al. Upwash exploitation and downwash avoidance by flap phasing in ibis formation flight. Nature 505, 399–402 (2014).
Fruchart, M., Hanai, R., Littlewood, P. B. & Vitelli, V. Non-reciprocal phase transitions. Nature 592, 363–369 (2021).
Dadhichi, L. P., Kethapelli, J., Chajwa, R., Ramaswamy, S. & Maitra, A. Nonmutual torques and the unimportance of motility for long-range order in two-dimensional flocks. Phys. Rev. E 101, 052601 (2020).
Xue, T., Li, X., Grassberger, P. & Chen, L. Swarming transitions in hierarchical societies. Phys. Rev. Res. 2, 042017 (2020).
Stein, J. C. Information production and capital allocation: decentralized versus hierarchical firms. J. Financ. 57, 1891–1921 (2002).
Mookherjee, D. Decentralization, hierarchies and incentives: a mechanism design perspective. J. Econ. Lit. 44, 367–390 (2006).
Hennart, J. F. in Organization Theory and the Multinational Corporation 157–181 (eds Ghoshal, S. & Westney, D. E.) (Palgrave Macmillan, 1993).
Bode, N. W., Faria, J. J., Franks, D. W., Krause, J. & Wood, A. J. How perceived threat increases synchronization in collectively moving animal groups. Proc. R. Soc. B Biol. Sci. 277, 3065–3070 (2010).
Bode, N. W., Franks, D. W. & Wood, A. J. Limited interactions in flocks: relating model simulations to empirical data. J. R. Soc. Interface 8, 301–304 (2011).
Huepe, C. & Aldana, M. Intermittency and clustering in a system of self-driven particles. Phys. Rev. Lett. 92, 168701 (2004).
Tunström, K. et al. Collective states, multistability and transitional behavior in schooling fish. PLoS Comput. Biol. 9, e1002915 (2013).
Trillmich, J., Fichtel, C. & Kappeler, P. M. Coordination of group movements in wild Verreaux’s sifakas (Propithecus verreauxi). Behaviour 141, 1103–1120 (2004).
Ariel, G. & Ayali, A. Locust collective motion and its modeling. PLoS Comput. Biol. 11, e1004522 (2015).
Kramer, D. L. & McLaughlin, R. L. The behavioral ecology of intermittent locomotion. Am. Zool. 41, 137–153 (2001).
Nathan, R. et al. A movement ecology paradigm for unifying organismal movement research. Proc. Natl Acad. Sci. USA 105, 19052–19059 (2008).
Strandburg-Peshkin, A., Papageorgiou, D., Crofoot, M. C. & Farine, D. R. Inferring influence and leadership in moving animal groups. Philos. Trans. R. Soc. B Biol. Sci. 373, 20170006 (2018).
Leca, J.-B., Gunst, N., Thierry, B. & Petit, O. Distributed leadership in semifree-ranging white-faced capuchin monkeys. Anim. Behav. 66, 1045–1052 (2003).
Gascuel, H.-M., Peruani, F. & Bon, R. Identifying interaction neighbours in animal groups. Anim. Behav. 174, 97–104 (2021).
Conradt, L. & Roper, T. J. Consensus decision making in animals. Trends Ecol. Evol. 20, 449–456 (2005).
Strömbom, D. Collective motion from local attraction. J. Theor. Biol. 283, 145–151 (2011).
Ferrante, E., Turgut, A. E., Dorigo, M. & Huepe, C. Elasticity-based mechanism for the collective motion of self-propelled particles with springlike interactions: a model system for natural and artificial swarms. Phys. Rev. Lett. 111, 268302 (2013).
Pearce, D. J., Miller, A. M., Rowlands, G. & Turner, M. S. Role of projection in the control of bird flocks. Proc. Natl Acad. Sci. USA 111, 10422–10426 (2014).
Barberis, L. & Peruani, F. Large-scale patterns in a minimal cognitive flocking model: incidental leaders, nematic patterns and aggregates. Phys. Rev. Lett. 117, 248001 (2016).
Herbert-Read, J. E. Understanding how animal groups achieve coordinated movement. J. Exp. Biol. 219, 2971–2983 (2016).
Lavergne, F. A., Wendehenne, H., Bäuerle, T. & Bechinger, C. Group formation and cohesion of active particles with visual perception-dependent motility. Science 364, 70–74 (2019).
Charlesworth, H. J. & Turner, M. S. Intrinsically motivated collective motion. Proc. Natl Acad. Sci. USA 116, 15362–15367 (2019).
Strömbom, D., Hassan, T., Hunter Greis, W. & Antia, A. Asynchrony induces polarization in attraction-based models of collective motion. R. Soc. Open Sci. 6, 190381 (2019).
Romanczuk, P., Couzin, I. D. & Schimansky-Geier, L. Collective motion due to individual escape and pursuit response. Phys. Rev. Lett. 102, 010602 (2009).
Strömbom, D. et al. Bistability and switching behavior in moving animal groups. Northeast J. Complex Syst. 4, 1 (2022).
Strandburg-Peshkin, A. et al. Visual sensory networks and effective information transfer in animal groups. Curr. Biol. 23, R709–R711 (2013).
Agudo-Canalejo, J. & Golestanian, R. Active phase separation in mixtures of chemically interacting particles. Phys. Rev. Lett. 123, 018101 (2019).
Gastil, J. A definition and illustration of democratic leadership. Hum. Relat. 47, 953–975 (1994).
Galton, F. Vox populi (the wisdom of crowds). Nature 75, 450–451 (1907).
Acknowledgements
We thank A. Dusstour, A. Kacelnik and A. Perna for discussions and comments on the text. We also thank Montpellier Supagro Research Station (Domaine du Merle) and M.-H. Pillot for technical support in herd management and data acquisition. L.G.-N. acknowledges support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC 2002/1 ‘Science of Intelligence’—project 390523135. F.P. acknowledges financial support from CY Initiative of Excellence (grant ‘Investissements d’Avenir’ ANR-16-IDEX-0008), INEX 2021 Ambition project ‘Collective Intelligence’ (CollInt) [2021-008, CYIn-AAP2021-AmbEm-0000000031] and Labex MME-DII, projects 2021-258 and 2021-297.
Author information
Authors and Affiliations
Contributions
L.G.-N., R.B. and F.P. designed the study, performed statistical analysis of the data and derived the mathematical models used to interpret the data.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Cristian Huepe and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Experimental setup and characteristic times.
a, Scheme of the experimental setup, consisting of 4 adjacent arenas (area of 80 × 80 meters each one), with a 7-meter-high tower placed in the middle. The tower was used to acquire the videos, that would later be used to get the tracking of the individuals. b, Probability distribution of the duration times tCMP of the Collective Motion Phases (CMPs) observed in the experiments. c, Probability distribution of the duration times tGP of the Grazing Phases (GPs) observed in the experiments.
Extended Data Fig. 2 Quantifying the speed of individuals during CMPs.
a, Probability distribution P(v) of the individual velocities. This distribution allows us to define a threshold velocity vth = 0.45 m/s, which is the local minimum of the fit, depicted with a solid black line. b, Instantaneous velocities vi(t) of all the individuals of the group during one CMP. c, Average individual velocity 〈v〉CMP for all CMPs. The red line is the mean value over all CMPs, and the light red region represents the standard deviation. Figures a–c correspond to experiments with groups of N = 4 individuals, but are representative for all group sizes.
Extended Data Fig. 3 Characterization of CMPs.
a–c, Probability of finding a neighbour in a given direction as function of the rank of individuals within the line for group sizes N = 2, 3 and 4. d–i, Quantification of the orientational and spatial order by the average order parameter values 〈P〉 and 〈ψ〉 for all group sizes and for all CMPs. Data are presented as mean values (blue circles) ± SD computed over the whole duration of the corresponding CMP for each group size N = 2, 3 and 4. The red line depicts the mean value of the order parameters -〈P〉 and 〈ψ〉 - across all CMPs.
Extended Data Fig. 4 Quantification of leadership over many CMPs.
Probability distributions of playing the role of leader during a CMP, using m = 4. The blue bars represent the experimental results, and the red dots correspond to the binomial distribution B(n, m) that is associated to the null hypothesis that assumes that all individuals are equally probable to become CMP leader.
Extended Data Fig. 5 Quantification of leadership based on the statistics of the individual that acted as CMP leader most times.
The red histograms correspond to the χ2 distributions obtained from numerical simulations. The blue vertical line corresponds to the experimental measured χ2 value.
Extended Data Fig. 6 Exit-times distributions.
Histograms of the exit times of uninformed individuals obtained with the two models. a, The results for model P and IN3 are shown. b, The results for model V and IN3 are shown. c, Comparison between the average exit times obtained by using model P and three different interaction networks, namely IN1, IN2 and IN3.The results between IN3 and the other networks (IN1 and IN2) are significantly different. We used the Welch’s two-sided unequal variances t-test to quantify this hypothesis. In both comparisons (between IN3 and IN1, and between IN3 and IN2), the resulting p-value resulted to be p < 0.005. This confirms that the results between IN3 and the other two interaction networks - IN1 and IN2 - are significantly different. This is highlighted with the label ’***’. No adjustments were made for multiple comparisons. Data are presented as mean values ± SD.
Extended Data Fig. 7 Quantification of navigation accuracy.
Scheme of a sequence of CMPs of a group of N individuals. The light-grey trajectory is meant to follow the centre of mass of the group xg. The target is set on the x-axis at a distant position from the origin. The positions labelled as xg(tn) are the positions in space of the centre of mass of the group after n CMPs. Let us recall that each CMP possesses a leader.
Extended Data Fig. 8 Effect of the interaction network for multiple target scenario.
The figure shows the superposition of individual trajectories of 300 simulations using interaction network IN1, IN2, and IN3 and model P.
Supplementary information
Supplementary Information
The Supplementary Information contains mainly details on the experimental set-up, data acquisition and fitting of the experimental data using the models explained in the main text (model P, model V and model V + P).
Supplementary Video 1
Tracking of a sequence of four CMPs extracted from a trial with a group of size N = 4, where each individual adopts the leading position one time.
Supplementary Video 2
Alternating collective motion phases (CMPs) and grazing phases (GPs) observed in the experiments (raw data) for all group sizes (N = 2, 3 and 4).
Supplementary Video 3
Tracking of CMPs for group size N = 4.
Supplementary Video 4
Numerical simulations of the exploration of the maze shown in Fig. 4c in the main text for a group of size N = 4 using model P.
Supplementary Video 5
Numerical simulations of the exploration of the maze shown in Fig. 4c in the main text for a group of size N = 4 using model V.
Supplementary Video 6
Video taken by Richard Bon (Université Paul Sabatier, CRCA, Toulouse, France) of a large group of moving sheep. The video was taken in the Alps.
Supplementary Video 7
Numerical simulations implemented for the generalized model using a generalized network IN3 and a group of N = 40 individuals. The probability of following a neighbour from the back is p0 = 0.8 (Methods).
Supplementary Video 8
Numerical simulations implemented using our model (model P + IN3) and a group of N = 4 individuals. For aesthetic reasons, we included a more detailed implementation for the transition of the individuals between CMP and GP. For the realization of the video, we used a constant time interval between transitions of the individuals in such a way that the leader (rank K = 1) makes the transition at a given time t1, then the first follower (rank K = 2) makes the transition at time t2 = t1 + dt, the third follower (K = 3) makes the transition at time t3 = t2 + dt and so on. This implementation was used for both transitions: CMP → GP and GP → CMP. For the video, we used dt = 5 time units.
Supplementary Video 9
Numerical simulations implemented using a generalization of the model presented in Barberis et al.5, which is a generic model that considers restricted vision angles of the particles.
Source data
Source Data Fig. 1
Data used for the plots in Figure 1b–e.
Source Data Fig. 2
Data used for the plots in Figure 2c,d.
Source Data Fig. 4
Data used for the plots in Figure 4b,d,e,g.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Gómez-Nava, L., Bon, R. & Peruani, F. Intermittent collective motion in sheep results from alternating the role of leader and follower. Nat. Phys. 18, 1494–1501 (2022). https://doi.org/10.1038/s41567-022-01769-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01769-8
This article is cited by
-
Dynamical order and many-body correlations in zebrafish show that three is a crowd
Nature Communications (2024)
-
Majority networks and local consensus algorithm
Scientific Reports (2023)
-
Collective motion strategies of sheep
Nature Reviews Physics (2023)
-
Sheep lead the way
Nature Physics (2022)