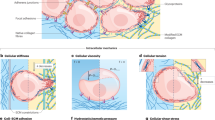
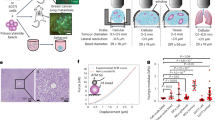
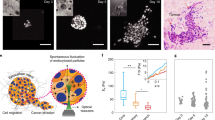
Abstract
Palpation utilizes the fact that solid breast tumours are stiffer than the surrounding tissue. However, cancer cells tend to soften, which may enhance their ability to squeeze through dense tissue. This apparent paradox proposes two contradicting hypotheses: either softness emerges from adaptation to the tumour’s microenvironment or soft cancer cells are already present inside a rigid primary tumour mass giving rise to cancer cell motility. We investigate primary tumour explants from patients with breast and cervix carcinomas on multiple length scales. We find that primary tumours are highly heterogeneous in their mechanical properties on all scales from the tissue level down to individual cells. This results in a broad rigidity distribution—from very stiff cells to cells softer than those found in healthy tissue—that is shifted towards a higher fraction of softer cells. Atomic-force-microscopy-based tissue rheology reveals that islands of rigid cells are surrounded by soft cells. The tracking of vital cells confirms the coexistence of jammed and unjammed areas in tumour explants. Despite the absence of a percolated backbone of stiff cells and a large fraction of unjammed, motile cells, cancer cell clusters show a heterogeneous solid behaviour with a finite elastic modulus providing mechanical stability.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
All data are available upon request from the corresponding author.
Code availability
Simulation data and code are available from D.B. (d.bi@northeastern.edu) on reasonable request.
References
Friedman, E., Verderame, M., Winawer, S. & Pollack, R. Actin cytoskeletal organization loss in the benign-to-malignant tumor transition in cultured human colonic epithelial cells. Cancer Res. 44, 3040–3050 (1984).
Cross, S. E., Jin, Y.-S., Rao, J. & Gimzewski, J. K. Nanomechanical analysis of cells from cancer patients. Nat. Nanotechnol. 2, 780–783 (2007).
Lekka, M. et al. Elasticity of normal and cancerous human bladder cells studied by scanning force microscopy. Eur. Biophys. J. 28, 312–316 (1999).
Guck, J., Ananthakrishnan, R., Moon, T. J., Cunningham, C. C. & Käs, J. Optical deformability of soft biological dielectrics. Phys. Rev. Lett. 84, 5451–5454 (2000).
Tse, H. T. K. et al. Quantitative diagnosis of malignant pleural effusions by single-cell mechanophenotyping. Sci. Transl. Med. 5, 212ra163 (2013).
Karantza, V. Keratins in health and cancer: more than mere epithelial cell markers. Oncogene 30, 127–138 (2011).
Yang, J. et al. Guidelines and definitions for research on epithelial–mesenchymal transition. Nat. Rev. Mol. Cell Biol. 21, 341–352 (2020).
Seltmann, K., Fritsch, A. W., Käs, J. A. & Magin, T. M. Keratins significantly contribute to cell stiffness and impact invasive behavior. Proc. Natl Acad. Sci. USA 110, 18507–18512 (2013).
Friedl, P., Wolf, K. & Lammerding, J. Nuclear mechanics during cell migration. Curr. Opin. Cell Biol. 23, 55–64 (2011).
Xia, Y., Pfeifer, C. R. & Discher, D. E. Nuclear mechanics during and after constricted migration. Acta Mech. Sin. 35, 299–308 (2019).
Runge, J. et al. Evaluation of single-cell biomechanics as potential marker for oral squamous cell carcinomas: a pilot study. Oral Dis. 20, e120–e127 (2014).
Nel, I., Morawetz, E. W., Tschodu, D., Käs, J. A. & Aktas, B. The mechanical fingerprint of circulating tumor cells (CTCs) in breast cancer patients. Cancers 13, 1119 (2021).
Oktay, M. H. et al. Correlated immunohistochemical and cytological assays for the prediction of hematogenous dissemination of breast cancer. J. Histochem. Cytochem. 60, 168–173 (2012).
Plodinec, M. et al. The nanomechanical signature of breast cancer. Nat. Nanotechnol. 7, 757–765 (2012).
Grosser, S. et al. Cell and nucleus shape as an indicator of tissue fluidity in carcinoma. Phys. Rev. X 11, 11033 (2021).
Helmlinger, G., Netti, P. A., Lichtenbeld, H. C., Melder, R. J. & Jain, R. K. Solid stress inhibits the growth of multicellular tumor spheroids. Nat. Biotechnol. 15, 778–783 (1997).
Jonietz, E. Mechanics: the forces of cancer. Nature 491, S56–S57 (2012).
Godard, B. G. & Heisenberg, C.-P. Cell division and tissue mechanics. Curr. Opin. Cell Biol. 60, 114–120 (2019).
Ranft, J. et al. Fluidization of tissues by cell division and apoptosis. Proc. Natl Acad. Sci. USA 107, 20863–20868 (2010).
Guevorkian, K., Colbert, M.-J., Durth, M., Dufour, S. & Brochard-Wyart, F. Aspiration of biological viscoelastic drops. Phys. Rev. Lett. 104, 218101 (2010).
Pawlizak, S. et al. Testing the differential adhesion hypothesis across the epithelial–mesenchymal transition. New J. Phys. 17, 83049 (2015).
Angelini, T. E. et al. Glass-like dynamics of collective cell migration. Proc. Natl Acad. Sci. USA 108, 4714–4719 (2011).
Nnetu, K. D., Knorr, M., Käs, J. & Zink, M. The impact of jamming on boundaries of collectively moving weak-interacting cells. New J. Phys. 14, 115012 (2012).
Collins, T. A., Yeoman, B. M. & Katira, P. To lead or to herd: optimal strategies for 3D collective migration of cell clusters. Biomech. Model. Mechanobiol. 19, 1551–1564 (2020).
Ilina, O. et al. Cell–cell adhesion and 3D matrix confinement determine jamming transitions in breast cancer invasion. Nat. Cell Biol. 22, 1103–1115 (2020).
Levental, K. R. et al. Matrix crosslinking forces tumor progression by enhancing integrin signaling. Cell 139, 891–906 (2009).
Pickup, M. W., Mouw, J. K. & Weaver, V. M. The extracellular matrix modulates the hallmarks of cancer. EMBO Rep. 15, 1243–1253 (2014).
Paszek, M. J. et al. Tensional homeostasis and the malignant phenotype. Cancer Cell 8, 241–254 (2005).
DuFort, C. C., Paszek, M. J. & Weaver, V. M. Balancing forces: architectural control of mechanotransduction. Nat. Rev. Mol. Cell Biol. 12, 308–319 (2011).
Raab, M. et al. Crawling from soft to stiff matrix polarizes the cytoskeleton and phosphoregulates myosin-II heavy chain. J. Cell Biol. 199, 669–683 (2012).
Teixeira, M. R. & Heim, S. Cytogenetic analysis of tumor clonality. Adv. Cancer Res. 112, 127–149 (2011).
Braun, J. et al. A compact 0.5 T MR elastography device and its application for studying viscoelasticity changes in biological tissues during progressive formalin fixation. Magn. Reson. Med. 79, 470–478 (2018).
Sauer, F. et al. Whole tissue and single cell mechanics are correlated in human brain tumors. Soft Matter 17, 10744–10752 (2021).
Sauer, F. et al. Collagen networks determine viscoelastic properties of connective tissues yet do not hinder diffusion of the aqueous solvent. Soft Matter 15, 3055–3064 (2019).
Bonfanti, A., Kaplan, J. L., Charras, G. & Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 16, 6002–6020 (2020).
Wu, P.-H. et al. A comparison of methods to assess cell mechanical properties. Nat. Methods 15, 491–498 (2018).
Jiang, X. et al. In vivo high-resolution magnetic resonance elastography of the uterine corpus and cervix. Eur. Radiol. 24, 3025–3033 (2014).
Streitberger, K.-J. et al. How tissue fluidity influences brain tumor progression. Proc. Natl Acad. Sci. USA 117, 128–134 (2020).
Hecht, F. M. et al. Imaging viscoelastic properties of live cells by AFM: power-law rheology on the nanoscale. Soft Matter 11, 4584–4591 (2015).
Hiratsuka, S. et al. The number distribution of complex shear modulus of single cells measured by atomic force microscopy. Ultramicroscopy 109, 937–941 (2009).
Guck, J. et al. The optical stretcher: a novel laser tool to micromanipulate cells. Biophys. J. 81, 767–784 (2001).
Honda, H. Description of cellular patterns by Dirichlet domains: the two-dimensional case. J. Theor. Biol. 72, 523–543 (1978).
Nagai, T. & Honda, H. A dynamic cell model for the formation of epithelial tissues. Philos. Mag. B 81, 699–719 (2001).
Atia, L. et al. Geometric constraints during epithelial jamming. Nat. Phys. 14, 613–620 (2018).
Mitchel, J. A. et al. In primary airway epithelial cells, the unjamming transition is distinct from the epithelial-to-mesenchymal transition. Nat. Commun. 11, 5053 (2020).
Park, J.-A. et al. Unjamming and cell shape in the asthmatic airway epithelium. Nat. Mater. 14, 1040–1048 (2015).
Honda, H. & Nagai, T. Cell models lead to understanding of multi-cellular morphogenesis consisting of successive self-construction of cells. J. Biochem. 157, 129–136 (2015).
Blauth, E., Kubitschke, H., Gottheil, P., Grosser, S. & Käs, J. A. Jamming in embryogenesis and cancer progression. Front. Phys. 9, 666709 (2021).
Li, X., Das, A. & Bi, D. Mechanical heterogeneity in tissues promotes rigidity and controls cellular invasion. Phys. Rev. Lett. 123, 058101 (2019).
Amack, J. D. & Manning, M. L. Knowing the boundaries: extending the differential adhesion hypothesis in embryonic cell sorting. Science 338, 212–215 (2012).
Sahu, P. et al. Small-scale demixing in confluent biological tissues. Soft Matter 16, 3325–3337 (2020).
Huang, J., Cochran, J. O., Fielding, S. M., Marchetti, M. C. & Bi, D. Shear-driven solidification and nonlinear elasticity in epithelial tissues. Phys. Rev. Lett. 128, 178001 (2022).
Labernadie, A. et al. A mechanically active heterotypic E-cadherin/N-cadherin adhesion enables fibroblasts to drive cancer cell invasion. Nat. Cell Biol. 19, 224–237 (2017).
Merkel, M., Baumgarten, K., Tighe, B. P. & Manning, M. L. A minimal-length approach unifies rigidity in underconstrained materials. Proc. Natl Acad. Sci. USA 116, 6560–6568 (2019).
Damavandi, O. K., Hagh, V. F., Santangelo, C. D. & Manning, M. L. Energetic rigidity. I. A unifying theory of mechanical stability. Phys. Rev. E 105, 025003 (2022).
Yan, L. & Bi, D. Multicellular rosettes drive fluid-solid transition in epithelial tissues. Phys. Rev. X 9, 011029 (2019).
Das, A., Sastry, S. & Bi, D. Controlled neighbor exchanges drive glassy behavior, intermittency, and cell streaming in epithelial tissues. Phys. Rev. X 11, 041037 (2021).
Bi, D., Yang, X., Marchetti, M. C. & Manning, M. L. Motility-driven glass and jamming transitions in biological tissues. Phys. Rev. X 6, 021011 (2016).
Mierke, C. T. The matrix environmental and cell mechanical properties regulate cell migration and contribute to the invasive phenotype of cancer cells. Rep. Prog. Phys. 82, 064602 (2019).
Gensbittel, V. et al. Mechanical adaptability of tumor cells in metastasis. Dev. Cell 56, 164–179 (2021).
Nia, H. T., Munn, L. L. & Jain, R. K. Physical traits of cancer. Science 370, eaaz0868 (2020).
Greeley, C. F. & Frost, A. R. Cytologic features of ductal and lobular carcinoma in fine needle aspirates of the breast. Acta Cytol. 41, 333–340 (1997).
Conklin, M. W. et al. Aligned collagen is a prognostic signature for survival in human breast carcinoma. Am. J. Pathol. 178, 1221–1232 (2011).
Sharma, V. P. et al. SUN-MKL1 crosstalk regulates nuclear deformation and fast motility of breast carcinoma cells in fibrillar ECM microenvironment. Cells 10, 1549 (2021).
Basan, M., Risler, T., Joanny, J.-F., Sastre-Garau, X. & Prost, J. Homeostatic competition drives tumor growth and metastasis nucleation. HFSP J. 3, 265–272 (2009).
Liu, X. et al. Homophilic CD44 interactions mediate tumor cell aggregation and polyclonal metastasis in patient-derived breast cancer models. Cancer Discov. 9, 96–113 (2019).
Hammond, S. L., Ham, R. G. & Stampfer, M. R. Serum-free growth of human mammary epithelial cells: rapid clonal growth in defined medium and extended serial passage with pituitary extract. Proc. Natl Acad. Sci. USA 81, 5435–5439 (1984).
Rosa, M., Mohammadi, A. & Masood, S. The value of fine needle aspiration biopsy in the diagnosis and prognostic assessment of palpable breast lesions. Diagn. Cytopathol. 40, 26–34 (2012).
Lincoln, B., Wottawah, F., Schinkinger, S., Ebert, S. & Guck, J. High‐throughput rheological measurements with an optical stretcher. Methods Cell Biol. 83, 397–423 (2007).
Wetzel, F. et al. Single cell viability and impact of heating by laser absorption. Eur. Biophys. J. 40, 1109–1114 (2011).
Farhadifar, R. et al. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr. Biol. 17, 2095–2104 (2007).
Fletcher, A. G., Osterfield, M., Baker, R. E. & Shvartsman, S. Y. Vertex models of epithelial morphogenesis. Biophys. J. 106, 2291–2304 (2014).
Staple, D. B. et al. Mechanics and remodelling of cell packings in epithelia. Eur. Phys. J. E 33, 117–127 (2010).
Li, B. & Sun, S. X. Coherent motions in confluent cell monolayer sheets. Biophys. J. 107, 1532–1541 (2014).
Hufnagel, L., Teleman, A. A., Rouault, H., Cohen, S. M. & Shraiman, B. I. On the mechanism of wing size determination in fly development. Proc. Natl Acad. Sci. USA 104, 3835–3840 (2007).
Bi, D., Lopez, J. H., Schwarz, J. M. & Manning, M. L. A density-independent rigidity transition in biological tissues. Nat. Phys. 11, 1074–1079 (2015).
Yang, X. et al. Correlating cell shape and cellular stress in motile confluent tissues. Proc. Natl Acad. Sci. USA 114, 12663–12668 (2017).
Fujii, Y. et al. Spontaneous spatial correlation of elastic modulus in jammed epithelial monolayers observed by AFM. Biophys. J. 116, 1152–1158 (2019).
Wu, D. et al. CD138-negative myeloma cells regulate mechanical properties of bone marrow stromal cells through SDF-1/CXCR4/AKT signaling pathway. Biochim. Biophys. Acta 1853, 338–347 (2015).
Ciasca, G. et al. Nano-mechanical signature of brain tumours. Nanoscale 8, 19629–19643 (2016).
Bitzek, E., Koskinen, P., Gähler, F., Moseler, M. & Gumbsch, P. Structural relaxation made simple. Phys. Rev. Lett. 97, 170201 (2006).
Allen, M. P. & Tildesley, D. J. Computer Simulation of Liquids (Oxford Univ. Press, 2017).
Maloney, C. E. & Lemaître, A. Amorphous systems in athermal, quasistatic shear. Phys. Rev. E 74, 016118 (2006).
Clark, A. G. & Vignjevic, D. M. Modes of cancer cell invasion and the role of the microenvironment. Curr. Opin. Cell Biol. 36, 13–22 (2015).
Acknowledgements
We would like to thank A. Bruckert, J. Schnedemann and S. Klingkowski from Pathologie Hamburg-West, as well as F. Juliano from Montefiore Hospital, for the preparation of tissue samples. This work was funded by the German Science Foundation (DFG; KA1116/9-1 and KA1116/17-1), as well as project ‘FORCE’ within the EU’s Horizon 2020 research and innovation programme. Graduate students A.W.F., T.R.K., S.P. and F.W. were funded by fellowships of the DFG Excellence graduate school BuildMoNa. The research with A.N. was part of the joint project EXPRIMAGE funded by the German Federal Ministry for Education and Research (BMBF 13N9366). T.F. was funded by ERC Advanced Grant ‘HoldCancerBack’ (741350). D.B. and X.L. would like to acknowledge support from the Northeastern University TIER 1 Grant, National Science Foundation DMR-2046683; the Alfred P. Sloan Foundation; MathWorks Microgrants; and the Northeastern University Discovery Cluster. M.H.O. and J.C. were funded by CA255153. We would also like to acknowledge the Syracuse University HTC Campus Grid, NSF award ACI-1341006.
Author information
Authors and Affiliations
Contributions
J.A.K. planned and directed this study. T.F., D.B., X.L. and J.A.K. wrote the manuscript. All the authors discussed the results and commented on the manuscript. F.W. carried out experiments on the breast tumour cells and controls. A.W.F. and S.P. were responsible for the measurements of cervical samples. R.S., T.R.K., S.P., A.W.F., E.M. and F.W. developed a sample preparation and measurement routine. T.F., M.Z. and S.F. carried out the AFM measurements. F.S. carried out the MRE measurements. J.B. provided technical support for the MRE measurements. S.G. and J.L. performed the experiments on MTS. F.R. performed the experiments on tumour explants. B.A., L.-C.H., M.H., K.B., S.B., B.W., M.H.O., J.C. and A.N. provided the patient samples and scientific/medical advice for data interpretation. D.B., X.L., M.C.M. and M.L.M designed the theoretical and simulation models. D.B., X.L. and M.L.M. developed, executed and analysed the simulation results with oversight from J.A.K.
Corresponding author
Ethics declarations
Competing interests
The authors have no competing interests.
Peer review
Peer review information
Nature Physics thanks Dennis Discher, Sanjay Kumar and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Effect of passaging on the deformability of primary breast tumour and normal epithelial cells.
Left) Distribution of the maximum relative cell deformations (observed at t = 3 s) for a breast cancer sample stretched at the end of passage number 1-3 (sample size: P1 = 164 cells, P 2 = 496 cells, P3 = 309 cells). Right) Relative deformation distribution epithelial cells from breast reduction (HMEpC) stretched at the end of passage number 2 and 10 (sample size: P2 = 352 cells, P10 = 702 cells). With increasing passage number more and more deformable cells are found. Time between passaging was 7 to 10 days.
Extended Data Fig. 2 Individual Histograms of the relative deformation of breast tumour samples.
Cells isolated from 13 breast tumours were measured in the optical stretcher, 2 fibroadenomas (FA) and HMEpC cells serve as control. Log-Normal distributions were fitted to the histograms; details of the fits can be found in Extended Data Table 1.
Extended Data Fig. 3 Individual Histograms the relative deformation of Cervix Tumours.
Cells were isolated from 4 cervix tumours and normal cervix tissue from the same patient as control. Log-Normal distributions were fitted; details of the fits can be found in Extended Data Table 1.
Extended Data Fig. 4 The stream anisotropy as a function of fr for the invading cell.
The stream anisotropy as a function of fr for the invading cell.
Supplementary information
Supplementary Information
Supplementary Fig. 1.
Supplementary Video 1
Vital imaging of the tumour fragment. A small fragment of a cervix tumour was vital stained with SiR-DNA to record the movement of cell nuclei. The video is ×600 the real-time speed.
Supplementary Video 2
Cell nuclei tracking in the tumour fragment. We tracked the cell nuclei shown in Supplementary Video 1. The colour encodes the cell speed with blue colour representing slower cells and red colours representing faster cells.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Fuhs, T., Wetzel, F., Fritsch, A.W. et al. Rigid tumours contain soft cancer cells. Nat. Phys. 18, 1510–1519 (2022). https://doi.org/10.1038/s41567-022-01755-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01755-0