Topological nature of the liquid–liquid phase transition in tetrahedral liquids

Abstract

The first-order phase transition between two tetrahedral networks of different density—introduced as a hypothesis to account for the anomalous behaviour of certain thermodynamic properties of deeply supercooled water—has received strong support from a growing body of work in recent years. Here we show that this liquid–liquid phase transition in tetrahedral networks can be described as a transition between an unentangled, low-density liquid and an entangled, high-density liquid, the latter containing an ensemble of topologically complex motifs. We first reveal this distinction in a rationally designed colloidal analogue of water. We show that this colloidal water model displays the well-known water thermodynamic anomalies as well as a liquid–liquid critical point. We then investigate water, employing two widely used molecular models, to demonstrate that there is also a clear topological distinction between its two supercooled liquid networks, thereby establishing the generality of this observation, which might have far-reaching implications for understanding liquid–liquid phase transitions in tetrahedral liquids.

Main

A salient feature of liquid water is the anomalous behaviour of its thermodynamic response functions upon cooling, the most famous being the density maximum at ambient pressure^1,2,3,4,5,6. In an effort to explain the origin of water’s thermodynamic anomalies, enhanced in supercooled states, Poole et al. suggested the presence of a first-order liquid–liquid phase transition (LLPT) line in the supercooled region of the pressure–temperature (P–T) phase diagram⁷. In this scenario, this transition line separates two liquid phases formed of transient hydrogen-bond networks—the low-density liquid (LDL) and high-density liquid (HDL)—and terminates at a liquid–liquid critical point (LLCP)⁷. The anomalous behaviour of liquid water, along with water polyamorphism, was then suggested to be a manifestation of the presence of this LLPT. Recent numerical studies^8,9, as well as experiments^10,11,12 (despite the difficulties induced by the rapid formation of ice around the predicted critical temperature and pressure conditions), have provided strong support to this fascinating hypothesis.

Several order parameters, based on geometric or energetic criteria, have been proposed to characterize the transition^{13,14,15,16,17,18,19,20}. In particular, the local structure index¹³ and the r₅ parameter¹⁴—two order parameters that effectively measure the distance between the first and second coordination shells—have been routinely applied. However, along the years, it has become increasingly apparent that a proper description of the LLPT requires the development of order parameters which include information beyond that of the single-molecule neighbourhood. This led to the introduction of other order parameters, such as ζ (ref. ²¹), V₄ (ref. ¹⁵) and the total node communicability²⁰, which include some information on the connectivity properties of the hydrogen-bond network¹⁹. It has also become clear that network interpenetration^22,23,24 plays a key role in the LLPT in tetrahedral liquids^23,25,26,27, with the LDL being composed of a single random tetrahedral network and the HDL consisting of two (or more²³) disordered but locally interpenetrating networks. In this context, a structure-based order parameter that fundamentally distinguishes the two liquids at the microscopic level will be important to develop our understanding of the mechanism for achieving a difference in density and, hence, the physical origin of the LLPT.

A colloidal model of water

Colloidal patchy particles, due to their capacity to form network liquids via encoded self-assembly information²⁵, combined with their synthetic availability^{28,29,30,31,32}, are ideally suited to investigating universal aspects of the LLPT, as well as potentially facilitating detailed experimental investigations at single-particle resolution. Therefore, guided by recent advances in programming their hierarchical self-assembly³³ and in understanding the conditions necessary for facilitating a LLPT—bond flexibility^25,26 and network interpenetration^23,26—we rationally designed a colloidal analogue of water. Figure 1a schematically illustrates this ‘colloidal water’ model. We considered designer triblock patchy particles^28,30,34 with two distinct attractive patches that encode tetrahedrality—key to the uniqueness of water⁵. The tetrahedrality emerges as the triblock patchy particles undergo two-stage assembly upon cooling. The energetics and geometry of the patches, labelled A and B, encode the desired staged-assembly information into the particles^33,35,36. The energetics are chosen to facilitate the formation of discrete tetrahedral clusters, initially driven by strong A–A interactions, and then a tetrahedral network fluid via weaker B–B interactions (Fig. 1a and Supplementary Fig. S1). The width of the A patches is judiciously chosen so as to favour the formation of a tetrahedral cluster fluid upon completion of the first stage of assembly^33,35,36. The width of each B patch is instead chosen to favour its interaction with only one other B patch. The discrete tetrahedral clusters then behave as secondary building blocks, similar to tetrahedral patchy particles, that can interact with one another via B patches at lower temperatures to drive a second stage of assembly, leading to the formation of a liquid network. In this case, the patch widths are chosen not only to enforce the desired valency constraints but also to maximize the flexibility of the bonds to hinder the onset of crystallization²⁵. As a result, the tetrahedral clusters formed by the triblock patchy particles can deviate from the ideal, tetrahedral symmetry. Note that the volume occupied by a tetrahedral cluster is less than that of a spherical patchy particle of equivalent size (Fig. 1a), thereby easing the formation of locally interpenetrating networks.

Fig. 1: Thermodynamic anomalies and LLCP in colloidal water.

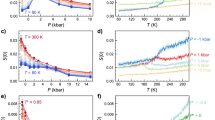
a, Schematic of the hierarchical self-assembly of triblock patchy particles leading to a colloidal model of water. The two patches, labelled A and B, are of different sizes and form bonds of different strengths. The A patches (red) form stronger bonds than the B patches (blue) so as to encode two-stage assembly upon cooling. b, The evolution of the reduced density ρ^⋆ as a function of the reduced temperature T^⋆ for different reduced pressures P^⋆, where P^⋆ × 10³ = 5, 6, 7, 7.5, 8.5, 9, 10, 12, 14 and 16. The arrow indicates the direction of increasing P^⋆. The inset highlights the density maximum for P^⋆ × 10³ = 5, 6, 7 and 7.5. c, The evolution of the reduced thermal expansion coefficient (${\alpha }_{P}^{\star}$), isothermal compressibility (${\kappa }_{T}^{\star}$) and isobaric heat capacity (${c}_{P}^{\star}$) as functions of T^⋆ at P^⋆ = 0.0085 (close to the critical pressure). Error bars represent the standard deviation over five sets of Monte Carlo trajectories, each of 1 × 10⁸ cycles. d, The dependence of ρ^⋆ and the fraction of BB bonds formed (f_b) on P^⋆ at T^⋆ = 0.105 and T^⋆ = 0.112. e, The distribution of the order parameter M for colloidal water (blue symbols), calculated using histogram reweighing, with T^⋆ ≈ 0.1075, P^⋆ ≈ 0.0082 and s ≈ 0.627, compared with the corresponding 3D Ising universal distribution (solid red line).

Thermodynamic anomalies of colloidal water

To establish that the chosen system of triblock patchy particles can indeed be considered as a colloidal analogue of water, we first demonstrate that it captures water’s thermodynamic anomalies. Figure 1b shows the reduced temperature (T^⋆ ≡ k_BT/ϵ_BB, where k_B is the Boltzmann constant and ϵ_BB is the well depth of patch B–patch B interactions) dependence of the reduced density (ρ^⋆ ≡ ρσ³, where σ is the hard-sphere diameter of a triblock patchy particle) along different isobars as determined by Monte Carlo simulations (Methods). Below a certain reduced pressure (P^⋆ ≡ Pσ³/ϵ_BB), the colloidal water model displays a density maximum upon cooling. Upon further cooling, ρ^⋆ approaches either a low or a high density value, depending on the pressure. Figure 1c shows the temperature dependence of the isobaric thermal expansion coefficient (${\alpha }_{P}^{\star}$), isothermal compressibility (${\kappa }_{T}^{\star}$) and isobaric heat capacity (${c}_{P}^{\star}$) at a select pressure, highlighting that, upon cooling, colloidal water shows non-monotonic behaviour in its thermodynamic response functions.

Figure 1d shows the dependence of ρ^⋆ and the fraction of bonds f_b (defined as the fraction of bonded B patches, a quantity directly reflective of the potential energy of the system) on P^⋆. We find that, below a certain T^⋆, there is a discontinuous jump in ρ^⋆ and f_b as P^⋆ changes, signalling a first-order phase transition. In contrast, ρ^⋆ and f_b change continuously with P^⋆ above this critical temperature, indicating that there is a LLCP. To locate the critical point, we followed a procedure similar to that applied recently in the study of a molecular model of water⁹ to calculate the order parameter distribution P(M), where M = ρ^⋆ − sv^⋆ is a combination of the density, the potential energy per particle (${v}^{\star}={{{\mathcal{V}}}}/(N{\varepsilon }_{{{{\rm{BB}}}}})$, where ${{{\mathcal{V}}}}$ is the total potential energy) and a field-mixing parameter s (ref. ³⁷). Upon performing a non-linear fit to identify the critical temperature (T_c) and critical pressure (P_c), we find that P(M) closely matches the distribution of the magnetization at the critical point of the three-dimensional (3D) Ising model (Fig. 1e), confirming the presence of an LLCP in colloidal water.

Topological nature of the LLPT in colloidal water

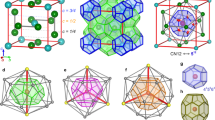
Topological concepts have become central in the description of physical^38,39,40, biological^41,42, social⁴³ and financial^44,45 networks. The topological properties of the interaction matrix,³⁹ owing to their unexpected connections with hidden conservation laws, have been shown to affect the response of the system to external perturbation and to play a key role in phase transitions. In this context, a pertinent question is whether the LLPT also has a topological character. Therefore, to identify any topological features, we inspected configurations of the LDL and HDL, finding that linked and knotted ring structures were noticeably present in the networks of the HDL phase but seemingly absent from the LDL phase. Figure 2a,b shows representative snapshots of the two liquid phases, where examples of these topologically complex motifs in the HDL networks are highlighted: a trefoil knot and a Hopf link⁴⁶ (Supplementary Video 1). In addition to knots and links, we found a large number of knotted theta curves^47,48 in the HDL networks, which can be viewed as two entangled fused rings (that is, rings that share at least two vertices). Examples of these knotted theta curves are shown in Fig. 2c and Supplementary Videos 2–4.

Fig. 2: Characterization of the LLPT in colloidal water by identifying links and knots.

a,b, Representative snapshots of the LDL (a) and HDL (b) networks of colloidal water at T^⋆ = 0.105, a temperature below the critical temperature T_c, and pressures either side of the critical pressure P_c (P^⋆ = 0.005 and P^⋆ = 0.016). Here, vertices correspond to the centres of tetrahedral clusters, while edges indicate existing B–B bonds. Tetrahedral clusters in the HDL network forming a trefoil knot (top) and a Hopf link (bottom) are highlighted in b, visualized in a reduced representation as tetrahedral patchy particles. c, Illustrative snapshots of theta curves found in the HDL networks and their corresponding idealized representations. d, The linking number (Lk) or writhe (Wr) for an idealized unknot (top left), unlink (top right), trefoil knot (bottom left) and Hopf link (bottom right). Each point in the motifs is coloured according to the corresponding (relative) contribution to the Gauss linking integral (equation (1)). e, The dependence of the average network linking number (${{{{\mathcal{L}}}}}_{\mathrm{n}}$) and the network writhe (${{{{\mathcal{W}}}}}_{\mathrm{n}}$) divided by the total number of rings in the network (${{{{\mathcal{N}}}}}_{{{{\rm{R}}}}}$) as a function of P^⋆ at T^⋆ = 0.105 (T < T_c) and T^⋆ = 0.112 (T > T_c). ${{{{\mathcal{L}}}}}_{n}$ and ${{{{\mathcal{W}}}}}_{n}$ were computed using rings of size up to ${l}_{\max }=13$. Error bars represent the standard deviation over two Monte Carlo trajectories, each of 4 × 10⁷ cycles. f, Frequency distribution for the writhe (Wr), separated for different unique knotted structures observed in the HDL network, at T^⋆ = 0.105 and P^⋆ = 0.016 with ${l}_{\max }=15$. The idealized knot associated with each distribution is colour coded and shown to the right of the plot. The dashed vertical lines indicate the writhe values of the idealized knots⁵⁷, and the solid lines through the data points are a guide to the eye.

To investigate the importance of such topological features in the LLPT, we quantified the degree of ‘entanglement’ in the LDL and HDL networks using the concept of helicity. The helicity has previously been used to provide a measure of the topological properties of vector fields, including magnetic fields⁴⁹ and vortex fields in fluids⁵⁰. This scalar quantity measures the amount of entwining in the set of closed curves contained within a system. For the particle-based networks considered here, these closed curves correspond to the set of rings formed by bonded particles. Each pair of disjoint (and therefore distinct) rings R_i and R_j contributes to the helicity with a term proportional, in essence, to how many times the two rings wind around one another (alternatively, this can be thought of as the number of times ring R_i pierces the surface bounded by ring R_j). Also, each individual ring contributes with a term proportional to how many times it loops around itself. Formally, the helicity is defined as a double sum over the total number of rings ${{{{\mathcal{N}}}}}_{{{{\rm{R}}}}}$ of the double line integral, known as the Gauss linking integral:

$${\mathcal{H}}=\mathop{\sum }\limits_{i=1}^{{\mathcal{N}}_{\mathrm{R}}}\mathop{\sum }\limits_{j\ge i}^{{\mathcal{N}}_{\mathrm{R}}}\frac{1}{4\uppi }{\oint }_{\!\!{\mathrm{R}}_{i}}{\oint }_{\!\!{\mathrm{R}}_{j}}\frac{{\mathbf{r}}_{j}-{\mathbf{r}}_{i}}{| {\mathbf{r}}_{j}-{\mathbf{r}}_{i}{| }^{3}}\cdot ({\mathrm{d}}{\mathbf{r}}_{j}\times {\mathrm{d}}{\mathbf{r}}_{i}),$$

(1)

where r_i and r_j are points on the two rings R_i and R_j, respectively. In equation (1), dr_i and dr_j are infinitesimal vectors tangential to the two rings R_i and R_j located at points r_i and r_j, respectively. In the case where i ≠ j, the Gauss linking integral gives the linking number (Lk_ij) of the two curves and takes on only integer values, whereas for i = j, it corresponds to the writhe (Wr_i) of a single curve and can take on any real value. Equation (1) can therefore be rewritten as the sum of the linking number and the writhe as

$${{{\mathcal{H}}}}=\mathop{\sum }\limits_{i > j}^{{{{{\mathcal{N}}}}}_{{{{\rm{R}}}}}}L{k}_{ij}+\mathop{\sum }\limits_{i=1}^{{{{{\mathcal{N}}}}}_{{{{\rm{R}}}}}}W{r}_{i}.$$

(2)

A visual representation of the Gauss linking integral for a set of closed loops, along with their corresponding writhe or linking number, is shown in Fig. 2d.

To establish the prevalence of topologically complex motifs in a liquid network, we adapted the concept of the helicity to define two quantities: the network linking number³⁹ (${{{{\mathcal{L}}}}}_{\mathrm{n}}$) and the network writhe (${{{{\mathcal{W}}}}}_{\mathrm{n}}$). To emphasize the degree of entanglement in a network, ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{n}$ are computed by summing up the absolute values of Lk_ij and Wr_i, respectively, to ignore the intrinsic orientation of the closed curves (in other words, we ignore the chirality of the topological objects). Additionally, the writhe is only computed for the set ${{{{\mathcal{N}}}}}_{{{{\rm{k}}}}}$ of knotted objects that includes knotted rings and pairs of fused rings that contain a knotted path. Including the latter in ${{{{\mathcal{N}}}}}_{{{{\rm{k}}}}}$ ensures that the contributions of theta curves (such as those shown in Fig. 2c) are captured by ${{{{\mathcal{W}}}}}_{\mathrm{n}}$. We formally define ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ as

$${{{{\mathcal{L}}}}}_{\mathrm{n}}=\mathop{\sum }\limits_{i > j}^{{{{{\mathcal{N}}}}}_{{{{\rm{R}}}}}}| L{k}_{ij}| \quad {{{\rm{and}}}}\quad {{{{\mathcal{W}}}}}_{\mathrm{n}}=\mathop{\sum }\limits_{i=1}^{{{{{\mathcal{N}}}}}_{{{{\rm{k}}}}}}| W{r}_{i}|$$

(3)

We also note that, in some instances, the helicity can include a twist term when the structures under consideration are constructed from bundles of closed curves (as is the case for supercoiled DNA). However, since this is not the case with the bond rings considered here, the twist can practically be ignored.

We computed ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ by first identifying all the rings in the system up to a maximum size of ${l}_{\max }$ (which defines the maximum number of particles forming a ring) and then calculating either (1) the linking number for all disjoint rings or (2) the writhe for each ring that is knotted and for entangled fused rings (such as the knotted theta curves shown in Fig. 2c). This then becomes akin to identifying linked and knotted paths in the spatial embedding of a graph^48,51 (full details on how ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ are computed in practice are given in Methods). Because we only identified links between rings of sizes $l\le {l}_{\max }$ and knotted structures of sizes $l\le (2{l}_{\max }-2)$, the computed values of ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ depend on the chosen ${l}_{\max }$. The LDL and HDL networks were found to show asymptotic limiting behaviour in their topological properties as a function of ${l}_{\max }$, above a critical value (Supplementary Figs. S2 and S3). Therefore, we computed ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ using the smallest ${l}_{\max }$ value that was found to be in the asymptotic regions of both the LDL and HDL phases (${l}_{\max }\ge 13$). Figure 2e shows the average values of ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ as a function of pressure for T < T_c and T > T_c with ${l}_{\max }=13$. Both ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ display a discontinuous change with pressure for sub-critical temperatures (T < T_c), concomitant with the discontinuity in the density (Fig. 1d), while they change continuously for super-critical temperatures.

The transition between the LDL and HDL phases is clearly captured by ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ when ${l}_{\max }\ge 5$ (Extended Data Fig. 1). However, as knots require longer chains of particles to form, they require a larger ${l}_{\max }$ to be identified, and so, ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ only shows a clear discontinuity when ${l}_{\max }\ge 10$ (Extended Data Fig. 1). Additionally, this means that there are fewer knots than links in the network, which in turn, means that ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ is smaller than ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ for a given ${l}_{\max }$. Yet, there are a variety of knotted objects in the HDL networks that contribute to the nonzero value of ${{{{\mathcal{W}}}}}_{\mathrm{n}}$. Figure 2f shows the frequency distribution of the writhe for different knotted objects found in the HDL network with ${l}_{\max }=15$. The majority of these structures contain trefoil knots, but we also find figure-of-eight, cinquefoil, three-twist and Stevedore knots⁴⁶. Similar to randomly generated knotted rings, the ensemble average of the writhe for each of these knots correlates well with the writhe of the corresponding idealized configuration (an idealized knot configuration is one which allows the volume-to-surface area ratio to be maximized⁵²).

Topological nature of the LLPT in molecular water

It is clear that both ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ can serve as a topological order parameter to describe the LLPT in colloidal water, providing strong evidence that the LLPT is a transition from an ‘unentangled’ to an ‘entangled’ network. This raises the question of whether entanglement also underpins the LLPT in supercooled water. Recently, it was shown that both the TIP4P/Ice⁵³ and TIP4P/2005⁵⁴ molecular models of water, which do not explicitly enforce tetrahedral coordination, exhibit a first-order LLPT and corresponding LLCP⁹. We therefore performed a similar topological analysis for TIP4P/Ice and TIP4P/2005. Figure 3a,b shows representative snapshots of the hydrogen-bond networks for the LDL and HDL of TIP4P/Ice. We find that the LDL contains a small number of links and practically no knotted structures (with only one or two knots occasionally appearing in a frame), while the HDL contains trefoil knots and theta curves in addition to links (which are also present in more abundance than in the LDL). Figure 3c shows that the ensemble average of the writhe for these trefoil motifs in the HDL of TIP4P/Ice also correlates well with the writhe of the idealized trefoil knot, as was the case for colloidal water. Additionally, as for colloidal water, Fig. 3d shows that, for TIP4P/Ice, both ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ jump at the critical pressure, suggesting that entanglement also underpins the LLPT in molecular water.

Fig. 3: Characterization of the LLPT in molecular water by identifying links and knots.

a,b, Illustrative snapshots of the LDL (a) and HDL (b) hydrogen-bond networks of molecular water, simulated using the TIP4P/Ice potential, at T = 188K and P = 1,100 bar and P = 2,000 bar, respectively. This temperature is slightly below the critical temperature (T_c = 188.8 K (ref. ⁹)), and the pressures are below and above the critical pressure (P_c = 1,725 bar (ref. ⁹)). In the LDL, only a few links are present (one is highlighted in a). In the HDL, both linked and knotted motifs are present (highlighted in b). c, The frequency distribution of the writhe (Wr) of the knotted paths found in the HDL network (essentially all being trefoil knots) at T = 188 K and P = 2,000 bar. The inset shows the idealized configuration of a trefoil knot, and the dotted vertical line indicates the value of the writhe for the idealized trefoil knot⁵⁷. d, Dependence of ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$, computed using rings of sizes up to ${l}_{\max }=13$, divided by ${{{{\mathcal{N}}}}}_{{{{\rm{R}}}}}$, as a function of P at T = 188 K for N = 1,000 molecules. Error bars represent the standard deviation as calculated along the corresponding molecular dynamics trajectory. e, The fluctuations in the density (ρ) and ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ (computed using ${l}_{\max }=13$) with time (t) along an isobaric–isothermal molecular dynamics trajectory for N = 300 molecules of TIP4P/Ice water at a temperature of T = 188 K for P = 1,100 bar, P = 1,725 bar and P = 2,000 bar.

A universal property of systems close to a second-order critical point (when T ≈ T_c and P ≈ P_c) is wide oscillations in relevant order parameters, as configurations belonging to both phases are sampled along the trajectory³⁷. To check whether the topological order parameter ${{{{\mathcal{L}}}}}_{n}$ does indeed properly distinguish between the two liquid phases of the TIP4P/Ice and TIP4P/2005 models, we calculated ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ along 40 μs molecular dynamics trajectories of supercooled water for different values of P close to T_c. Figure 3e shows the evolution of ρ and ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ along the molecular dynamics trajectory for a system of N = 300 TIP4P/Ice molecules at three different pressures. Above and below the critical pressure, ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ displays quite different values, indicating a notable topological difference between the two liquids. At the critical pressure, wide fluctuations in ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ are observed, closely correlating with those of ρ. Extended Data Fig. 2 shows that the TIP4P/2005 model also displays these wide fluctuations in ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ρ when P ≈ P_c, confirming that the LLPT can indeed be interpreted as a topological transition.

Conclusions

We have designed a colloidal analogue of water—a tetrahedral network liquid self-assembled from designer triblock patchy colloidal particles via tetrahedral clusters. This colloidal water model captures the anomalous thermodynamic behaviour of supercooled water, including the well-known density maximum, and displays two structurally different network liquid phases. With the synthetic feasibility of the triblock patchy particles under consideration³⁰, colloidal water presents itself as an ideal model system, amenable to experimental investigation at the single-particle level, for gleaning fundamental understanding of LLPTs in tetrahedral liquids.

By analysing configurations from this colloidal model and from two widely used molecular models⁵³ for water, we have established that the LDL and HDL networks associated with the LLPT in all three cases are topologically distinguishable. The LDL in all these cases is practically an ‘unentangled network’, consisting primarily of unknots, while the HDL is an ‘entangled network’ containing an ensemble of topologically non-trivial motifs. For colloidal as well as molecular models, ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{n}$—metrics able to capture the degree of entanglement—act as suitable order parameters, highlighting that the LLPT can also be interpreted as a topological phase transition.

Uncovering the topological distinction between the LDL and HDL networks allows us to understand the physical mechanism underpinning the LLPT from a new perspective that sheds light on its microscopic origin. The LLPT occurs at low temperatures at which the system tends to form a liquid network with the maximum number of bonds possible. At low pressures, it is well established that this is achieved by forming an open random tetrahedral network. However, as the pressure increases, the system tends also to minimize its volume. In tetrahedral liquids, associated with this drive to maximize the number of bonds, there is an increase in the number of rings in the network. Due to the directionality of the interactions, the system cannot minimize its volume by simply deforming the rings while preserving the network connectivity because there is a limit to the flexibility of the bonds. Instead, the system is able to simultaneously minimize its volume and maximize the number of bonds in the network by forming knots and links. Additionally, we note that, unlike knots and links formed by covalently bonded chains or networks⁴⁰, the LDL and HDL are transient networks (that is, bonds are constantly breaking and forming) and so their topological state is not constant. Despite this evolution, the topological signatures for each phase are properly defined.

The helicity has been used previously to study knotted vortices in classical fluids⁵⁵ and superfluids⁵⁶, where these knots were found to untie via a universal topological mechanism. It would be of interest to use the metrics for the degree of entanglement used here to follow the nucleation of the LDL out of the HDL, and vice versa, to see whether this universal topological mechanism is also relevant in the context of the LLPT. Finally, owing to their topological complexity, these entangled liquids should possess physical properties^38,40 distinct from simple liquids, which will merit exploration.

Methods

Colloidal water model

We employed the Kern–Frenkel pair potential^58,59, which has been used extensively to study patchy particles. Each particle, with a hard-core diameter σ, has (at opposite poles) two distinct, circular attractive patches, labelled A and B, having half-angles of θ_A and θ_B, respectively. The effective potential for a pair of patchy particles v_ij is

$${v}_{ij}({{{{\bf{r}}}}}_{ij},{{{{\boldsymbol{\Omega }}}}}_{i},{{{{\boldsymbol{\Omega }}}}}_{j})={v}_{ij}^{{{{\rm{hs}}}}}({r}_{ij})+\mathop{\sum}\limits_{\alpha ,\beta =\{A,B\}}{v}_{\alpha \beta }^{{{{\rm{sw}}}}}({r}_{ij})f({{{{\bf{r}}}}}_{ij},{\hat{{{{\bf{n}}}}}}_{i}^{\alpha },{\hat{{{{\bf{n}}}}}}_{j}^{\beta }),$$

(4)

where r_ij = ∣r_ij∣ is the centre-to-centre distance between particles i and j and Ω_i and Ω_j describe the orientations of particles i and j, respectively. In equation (4), ${v}_{ij}^{{{{\rm{hs}}}}}$ is the hard-sphere pair potential, given by

$${v}_{ij}^{{{{\rm{hs}}}}}({r}_{ij})=\left\{\begin{array}{ll}\infty \quad &{{{\rm{if}}}}\ {r}_{ij} < \sigma \\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.$$

(5)

and ${v}_{ij}^{{{{\rm{sw}}}}}$ is a square-well potential, given by

$${v}_{\alpha \beta }^{{{{\rm{sw}}}}}({r}_{ij})=\left\{\begin{array}{ll}-{\varepsilon }_{\alpha \beta }\quad &{{{\rm{if}}}}\,\sigma \le {r}_{ij}\le (1+{\delta }_{\alpha \beta })\sigma \\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.,$$

(6)

where ε_αβ and δ_αβ control the depth and range, respectively, of patch α–patch β attraction. The factor $f({{{{\bf{r}}}}}_{ij},{\hat{{{{\bf{n}}}}}}_{i}^{\alpha },{\hat{{{{\bf{n}}}}}}_{j}^{\beta })$ controls the angular dependence of the interaction between two patches and is given by

$$f({{{{\bf{r}}}}}_{ij},{\hat{{{{\bf{n}}}}}}_{i}^{\alpha },{\hat{{{{\bf{n}}}}}}_{j}^{\beta })=\left\{\begin{array}{ll}1\quad &{{{\rm{if}}}}\,{\hat{{{{\bf{n}}}}}}_{i}^{\alpha }\cdot {\hat{{{{\bf{r}}}}}}_{ij} > \cos {\theta }_{\alpha } \; {{{\rm{and}}}} \; {\hat{{{{\bf{n}}}}}}_{j}^{\beta }\cdot {\hat{{{{\bf{r}}}}}}_{ji} > \cos {\theta }_{\beta }\\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.,$$

(7)

where ${\hat{{{{\bf{n}}}}}}_{i}^{\alpha }$ is a normalized vector from the centre of particle i in the direction of the centre of patch α on its surface, thus depending on Ω_i. Similarly, ${\hat{{{{\bf{n}}}}}}_{j}^{\beta }$ is a normalized vector from the centre of particle j in the direction of the centre of patch β, thus depending on Ω_j. The total potential energy of the system was calculated by summing over the contributions from all distinct pairs (${{{\mathcal{V}}}}={\sum }_{i\ne j}{v}_{ij}$).

We employed ε_AA = 5ε_BB along with ε_AB = 0 to encode a two-stage self-assembly process upon cooling³³. We selected θ_A = 50° and θ_B = 26° because this choice, combined with the interaction strengths, ensures that an A patch interacts with three other A patches (to yield discrete tetrahedral clusters at relatively high temperatures) while a B patch interacts with only one other B patch (to bring the tetrahedral clusters together to form a tetrahedral network liquid at lower temperatures). The choice of ε_AB = 0, which is realizable via DNA-mediated interactions, facilitates staged assembly and allows for the use of a wider A patch without compromising the formation of self-limiting tetrahedral clusters at intermediate temperatures. Note that the use of an A patch with θ_A = 50° makes the tetrahedral clusters flexible enough to hinder crystallization from the tetrahedral liquids formed at lower temperatures. The ranges of the interactions are set by δ_AA = 0.05 and δ_BB = 0.2 (the value of δ_AB being irrelevant since ε_AB = 0). The longer range of B–B interactions facilitates the formation of a tetrahedral network liquid at low temperatures. In the present study, we used reduced units: the length in units of σ, the energy in units of ε_BB and the temperature in units of ε_BB/k_B, with the Boltzmann constant set to k_B = 1.

Monte Carlo simulations of colloidal water

All the Monte Carlo simulations were carried out with systems of N = 1,000 triblock patchy particles contained in a cubic box under periodic boundary conditions, using the minimum image convention. Each triblock patchy particle was treated as a rigid body whose orientational degrees of freedom were represented by quaternions. The potential energy was calculated using a spherical cutoff of σ(1 + δ_BB), and a cell list was used for efficiency⁶⁰. To enhance sampling in systems composed of clusters, we employed a combination of translational and rotational single-particle and cluster moves, where the acceptance probability for a translational or rotational cluster move was taken as⁶⁰

$${{{\rm{acc}}}}(o\to n)=\min \left\{1,\exp \left[-\beta \left({{{\mathcal{V}}}}(n)-{{{\mathcal{V}}}}(o)\right)\right]\mathop{\prod}\limits_{i,j}\frac{1-{{{{\rm{P}}}}}_{n}(i,j)}{1-{{{{\rm{P}}}}}_{o}(i,j)}\right\}$$

(8)

where β = 1/k_BT, ${{{\mathcal{V}}}}(o)$ and ${{{\mathcal{V}}}}(n)$ correspond to the potential energy of the system before and after the cluster move, respectively, and P(i, j) represents the probability that particles i and j share a bond, that is, that the patches interact. We defined a cycle as the number of attempts, equal to the number of particles N, to move (rotate or translate) a particle or a cluster (with equal probability). Additionally, in isothermal-isobaric (NPT) simulations, we included one volume move, on average, per cycle. We performed cluster volume moves in the logarithmic space of the volume (that is, $\ln ({V}_{n})=\ln ({V}_{o})+{{\Delta }}V$), where each cluster’s centre of mass was scaled isotropically. Volume moves were accepted with probability⁶¹

$$\begin{array}{rcl}{{{\mathrm{acc}}}}({V}_{o}\to {V}_{n})=\min \left\{1,\exp \left[({N}_{{{{\mathrm{clstr}}}}}+1)\ln \left(\frac{{V}_{n}}{{V}_{o}}\right) \right.\right. \\- \left. \left. \beta P{{\Delta }}V-\beta {{\Delta }}{{{\mathcal{V}}}}\right]\mathop{\prod}\limits_{i,j}\frac{1-{{{{\mathrm{P}}}}}_{n}(i,j)}{1-{{{{\mathrm{P}}}}}_{o}(i,j)}\right\},\end{array}$$

(9)

where ${N}_{{{{\rm{clstr}}}}}$ is the number of discrete clusters identified in the system. In the context of an anticipated two-stage assembly of the patchy colloidal particles via a discrete set of clusters, formed by A–A bonds, we constructed a simple rule to move the discrete clusters. We took P(i, j) = 1 if two particles share an A–A bond, and P(i, j) = 0 otherwise. Therefore, to ensure detailed balance is satisfied, any proposed cluster or volume moves that created a new A–A bond between particles i and j were rejected.

At low temperatures (T^⋆ ≤ 0.12), two sets of simulations were carried out over the same range of state points, starting from a tetrahedral cluster fluid of triblock patchy particles, where the initial density was set to ρ^⋆ = 0.2 for one set of simulations and to ρ^⋆ = 0.4 for the other set. For each of these simulations, 3 × 10⁸ Monte Carlo cycles were performed to ensure that equilibrium was attained. At higher temperatures, 1 × 10⁸ Monte Carlo cycles were performed, starting with a density of ρ^⋆ = 0.4.

From the NPT simulations, we calculated the reduced isobaric thermal expansion coefficient (${\alpha }_{P}^{\star}$), isothermal compressibility (${\kappa }_{T}^{\star}$) and isobaric heat capacity (${c}_{P}^{\star}$) by computing the covariance and variance in the volume and enthalpy (H) as

$${\alpha }_{P}=\frac{\langle HV\rangle -\langle H\rangle \langle V\rangle }{N\langle V\rangle {k}_{{{{\rm{B}}}}}{T}^{2}}=\frac{{k}_{{{{\rm{B}}}}}}{{\varepsilon }_{{{{\rm{BB}}}}}}{\alpha }_{P}^{\star},$$

(10)

$${\kappa }_{T}=\frac{\langle {V}^{2}\rangle -{\langle V\rangle }^{2}}{N\langle V\rangle {k}_{{{{\rm{B}}}}}T}=\frac{{\sigma }^{3}}{{\varepsilon }_{{{{\rm{BB}}}}}}{\kappa }_{T}^{\star},$$

(11)

$${c}_{P}=\frac{\langle {H}^{2}\rangle -{\langle H\rangle }^{2}}{N{k}_{{{{\rm{B}}}}}{T}^{2}}={k}_{{{{\rm{B}}}}}{c}_{P}^{\star}.$$

(12)

These thermodynamic quantities, as well as the average density, were computed from five independent NPT simulations, consisting of 1 × 10⁸ Monte Carlo cycles, following equilibration at each temperature and pressure considered.

Molecular dynamics simulations of TIP4P/Ice and TIP4P/2005

Molecular dynamics simulations were performed for the TIP4P/Ice⁵³ and TIP4P/2005⁵⁴ water models in the NPT ensemble, using GROMACS.⁶² The integration time step was 2 fs. The Nosé–Hoover thermostat and the isotropic Parrinello–Rahman barostat, both with characteristic times of a few picoseconds, were used. Rigid constraints for the molecular model were implemented with a sixth-order linear constraint solver. The long-range electrostatic interactions were dealt with by using the particle-mesh Ewald method at fourth order. The cut-off distances for both the van der Waals and the real-space electrostatic interactions were fixed at 0.9 nm. For the TIP4P/Ice model, we focused on the T = 188 K isotherm for systems of N = 300 and 1,000 molecules, with pressures ranging from 1 bar to 4,000 bar. For the TIP4P/2005 model, we performed simulations at T = 177 K and P = 1,750 bar for a system of N = 300 molecules. The analysed trajectories were longer than 40 μs for both models, and equilibrated data from ref. ⁹ were used as starting configurations.

Cluster identification in the colloidal water model

We identified the tetrahedral clusters formed by the triblock patchy particles using the local order parameter, q_Td (which equals 1 for a perfect tetrahedron), defined as⁶³

$${q}_{{{{\rm{Td}}}}}=1-\frac{3}{8}\mathop{\sum }\limits_{i=1}^{{N}_{\mathrm{c}}-1}\mathop{\sum }\limits_{j=i+1}^{{N}_{\mathrm{c}}}{\left(\cos {\psi }_{ij}+\frac{1}{3}\right)}^{2},$$

(13)

where N_c = 4 is the number of particles in the cluster under consideration and ψ_ij is the angle subtended at the centre of the cluster by the two vectors joining the centre of particle i and particle j. We defined the set of neighbours for each particle i as those with which it shares a patch A–patch A bond. q_Td was then calculated for all distinct combinations of four particles including i from this set. All unique sets of four particles satisfying the condition q_Td > 0.99 were considered to form a tetrahedron.

Multiple histogram reweighting

To identify the location of the LLCP in the colloidal water system, we merged information collected from the Monte Carlo simulations to generate an estimate of the density of states, $\hat{{{\varOmega }}}(E,V)$. In the NPT ensemble, the partition function at a given pressure P and temperature T can be written as^9,64

$${{{\mathcal{Z}}}}(P,\beta )=\mathop{\sum}\limits_{E}\mathop{\sum}\limits_{V}\hat{{{\varOmega }}}(E,V){\mathrm{e}}^{-\beta (E+PV)}={\mathrm{e}}^{-\beta G(P,\beta )},$$

(14)

where E is the energy of the system, V is the volume and G is the Gibbs free energy. We estimated the density of states by performing R simulations at different temperatures and pressures, where the total set of state points considered was given by {T_i, P_i}, i = 1, …, R. For each simulation, a histogram (H_i) of the energies and volumes sampled was generated using data from C_i configurations spaced equally along the trajectory. We defined an estimate for the density of states at discrete values of energy and volume, using data from a single simulation, as

$${{{\varOmega }}}_{i}(E,V)=\frac{{{{{\rm{H}}}}}_{i}(E,V)}{{{{{{C}}}}}_{i}}{\mathrm{e}}^{+{\beta }_{i}(E+{P}_{i}V)}{\mathrm{e}}^{-{\beta }_{i}G({P}_{i},{\beta }_{i})}.$$

(15)

However, each of the R simulations only provides information of the density of states for a finite portion of the phase space. Hence, a better estimate was obtained by combining all the information gathered from the R simulations. This ‘best guess’ for the density of states was written as a linear combination of these individual estimates, combined with a weight factor ω_i(E, V), as

$$\begin{array}{rcl}{\hat{{{\varOmega }}}}^{\mathrm{b}}(E,V)&=&\mathop{\sum }\limits_{i=1}^{R}{\omega }_{i}(E,V){{{\varOmega }}}_{i}(E,V)\\ &=&\mathop{\sum }\limits_{i=1}^{R}{\omega }_{i}(E,V)\frac{{{{{\rm{H}}}}}_{i}(E,V)}{{{{{{C}}}}}_{i}}{\mathrm{e}}^{+{\beta }_{i}(E+{P}_{i}V)}{\mathrm{e}}^{-{\beta }_{i}G({P}_{i},{\beta }_{i})}\end{array}.$$

(16)

Conventionally, it is assumed that the ‘random’ variable H_i(E, V) has Poisson statistics. It then becomes possible to optimize equation (16) by minimizing the variance of ${\hat{{{\varOmega }}}}^{b}(E,V)$ using the method of Lagrange multipliers, under the constraint that $\mathop{\sum }\nolimits_{i}^{R}{\omega }_{i}=1$. As a result

$${\hat{{{\varOmega }}}}^{\mathrm{b}}(E,V)=\frac{\mathop{\sum }\nolimits_{i = 1}^{R}{{{{\rm{H}}}}}_{i}(E,V)}{\mathop{\sum }\nolimits_{i = 1}^{R}{\mathrm{e}}^{-{\beta }_{i}(E+{P}_{i}V)}{\mathrm{e}}^{+{\beta }_{i}G({P}_{i},{\beta }_{i})}{{{{{C}}}}}_{i}}$$

(17)

and

$${\mathrm{e}}^{-{\beta }_{i}G({P}_{i},{\beta }_{i})}=\mathop{\sum}\limits_{E}\mathop{\sum}\limits_{V}{\hat{{{\varOmega }}}}^{\mathrm{b}}(E,V){\mathrm{e}}^{-{\beta }_{i}(E+{P}_{i}V)}.$$

(18)

When the number of samples used to generate each of the R histograms is the same (that is, ∀i: C_i = C), the above equations can be simplified by writing

$$\begin{array}{rcl}S(E,V)/{k}_{{{{\mathrm{B}}}}} & = & \ln {\hat{{{\varOmega }}}}^{\mathrm{b}}(E,V)=\ln \left(\frac{\mathop{\sum }\nolimits_{i = 1}^{R}{{{{\mathrm{H}}}}}_{i}(E,V)}{{{{{C}}}}}\right) \\ && -\ln \left(\mathop{\sum }\limits_{i=1}^{R}{\mathrm{e}}^{-{\beta }_{i}(E+{P}_{i}V)}{\mathrm{e}}^{+{\beta }_{i}G({P}_{i},{\beta }_{i})}\right)\end{array}$$

(19)

and

$$G({P}_{i},{\beta }_{i})=-{k}_{{{{\rm{B}}}}}T\ln \left(\mathop{\sum}\limits_{E}\mathop{\sum}\limits_{V}{\mathrm{e}}^{S(E,V)/{k}_{{{{\rm{B}}}}}-{\beta }_{i}(E+{P}_{i}V)}\right).$$

(20)

Evaluation of the exponential terms can be numerically unstable, but rewriting these equations in terms of the entropy allows us to make use of $\ln ({\mathrm{e}}^{x})=a+\ln ({\mathrm{e}}^{x-a})$ to improve the numerical precision. Equations (19) and (20) can then be solved self-consistently via an iterative procedure, taking G_i = 0 for all i as an initial guess. We assume that the values of the Gibbs free energies have converged once the sum squared difference between consecutive estimates is less than a tolerance value of 10⁻⁷. The converged solutions provided an estimate for the values of G(P, β) up to some additive constant c. From these estimates, we obtained values for the density of states. It was, therefore, possible to predict the probability of observing a state with energy E and volume V at any relevant state point (P, β) using

(21)

Bond definition

In the case of colloidal water, the network is created by the patch B–patch B interactions, forming bonds that join discrete tetrahedral clusters. Owing to the square-well nature of the patch–patch interaction, searching for the existing bonds becomes equivalent to searching for all pairs of particles with pair interaction energy equal to −ϵ_BB.

For the TIP4P/Ice and TIP4P/2005 models, a bond between two water molecules was deemed to exist when a hydrogen bond was present. This was defined on the basis of a geometric criterion⁶⁵ by the conditions r < 0.35 nm and θ < 30°. Here, r is the intermolecular oxygen–oxygen distance and θ is the smallest among the four angles between the intramolecular O–H and the intermolecular O–O lines. As shown previously¹⁹, no ambiguity in the identification of hydrogen bonds remains if the Chandler–Luzar geometric criterion is applied using inherent structure configurations. These are the local potential energy minimum configurations reached via a steepest descent path that quenches the vibrational degrees of freedom. To evaluate the inherent structures, we used the steepest descent algorithm in GROMACS (compiled in double precision) with a force tolerance of 1 J mol⁻¹ nm⁻¹ and a maximum step size of 5 × 10⁻⁴ nm.

Ring statistics

We calculated the number of rings (${{{{\mathcal{N}}}}}_{{{{{\rm{R}}}}}_{l}}$) with sizes $l\in [4-{l}_{\max }]$ where each bond network was abstracted into a periodic undirected graph G. The vertices (V_G) of the graph represent the positions of the objects of interest (either the tetrahedral cluster centres or the oxygen atoms of the water molecules), and each of the edges (E_G) connects two bonded objects as defined above. We defined a ring as a closed path in this graph (that is, a path whose first and final vertices are the same). We excluded rings in which non-adjacent vertices are directly connected via an edge. For each vertex ${{\mathsf{V}}}_{{\mathsf{G}}}^{i}$ in the graph, we determined all distinct rings, sequentially identifying all rings associated with each vertex, using a depth-first search traversal, up to the chosen ${l}_{\max }$. To improve the efficiency of the analysis, following the extraction of all relevant paths starting from ${{\mathsf{V}}}_{{\mathsf{G}}}^{i}$ (and hence rings containing ${{\mathsf{V}}}_{{\mathsf{G}}}^{i}$), all edges connected to that vertex were removed from the graph before initiating the depth-first search traversal from ${{\mathsf{V}}}_{{\mathsf{G}}}^{i+1}$. We also accounted for the double counting of a ring, which arises from the undirected nature of the graph.

Linking number and writhe calculations

We measured the entanglement of liquid networks using metrics derived from the helicity, which is defined in equation (2), in terms of Lk_ij, the linking number between two independent closed curves R_i and R_j, and Wr_i, the writhe of a single closed curve. Both the linking number and the writhe can be defined as double line integrals^46,66,67,68:

$$L{k}_{ij}({\mathrm{R}}_{i},{\mathrm{R}}_{j})=\frac{1}{4\uppi }{\oint }_{\!\!{\mathrm{R}}_{i}}{\oint }_{\!\!{\mathrm{R}}_{j}}\frac{{\mathbf{r}}_{j}-{\mathbf{r}}_{i}}{| {\mathbf{r}}_{j}-{\mathbf{r}}_{i}{| }^{3}}\cdot ({\mathrm{d}}{\mathbf{r}}_{j}\times {\mathrm{d}}{\mathbf{r}}_{i}),$$

(22)

$$W{r}_{i}({\mathrm{R}}_{i})=\frac{1}{4\uppi }{\oint }_{\!\!{\mathrm{R}}_{i}}{\oint }_{\!\!{\mathrm{R}}_{i}}\frac{{\mathbf{r}}_{i}^{\prime}-{\mathbf{r}}_{i}}{| {\mathbf{r}}_{i}^{\prime}-{\mathbf{r}}_{i}{| }^{3}}\cdot ({\mathrm{d}}{\mathbf{r}}_{i}^{\prime}\times {\mathrm{d}}{\mathbf{r}}_{i}).$$

(23)

Note that equation (22) and (23) are combined together in equation (1) (the contributions i ≠ j and i = j, respectively). The closed curves from which we computed ${{{{\mathcal{L}}}}}_{\mathrm{n}}$ and ${{{{\mathcal{W}}}}}_{\mathrm{n}}$ are constructed from the set of rings identified in the liquid networks from both models, where r_i and r_j represent the positions of the objects that make up rings R_i and R_j, respectively. We calculated the linking number only for pairs of disjoint rings (rings not sharing any vertices), and the writhe for both knotted individual rings and for pairs of rings that share at least one edge that were also knotted (these pairs of rings can essentially be considered as composite rings with intra-ring edges).

Computing the linking number

The rings are composed of discrete line segments and so can be considered as closed polygonal paths. As a result, the linking number can be computed using the expression for polylines⁶⁹:

$$L{k}_{ij}({{{{\rm{R}}}}}_{i},{{{{\rm{R}}}}}_{j})=\frac{1}{4\uppi }\mathop{\sum}\limits_{kl}{\lambda }_{kl},$$

(24)

where λ_kl is the contribution to the Lk_ij from a pair of line segments k and l belonging to rings i and j, respectively, and

$$\begin{array}{rcl}{\lambda }_{kl} & = &{{{\mathrm{atan}}}}\left(\frac{{{{\bf{a}}}}\cdot ({{{\bf{b}}}}\times {{{\bf{c}}}})}{| {{{\bf{a}}}}| | {{{\bf{b}}}}| | {{{\bf{c}}}}| +({{{\bf{a}}}}\cdot {{{\bf{b}}}})| {{{\bf{c}}}}| +({{{\bf{c}}}}\cdot {{{\bf{a}}}})| {{{\bf{b}}}}| +({{{\bf{b}}}}\cdot {{{\bf{c}}}})| {{{\bf{a}}}}| }\right) \\&& +{{{\mathrm{atan}}}}\left(\frac{{{{\bf{c}}}}\cdot ({{{\bf{d}}}}\times {{{\bf{a}}}})}{| {{{\bf{c}}}}| | {{{\bf{d}}}}| | {{{\bf{a}}}}| +({{{\bf{c}}}}\cdot {{{\bf{d}}}})| {{{\bf{a}}}}| +({{{\bf{a}}}}\cdot {{{\bf{c}}}})| {{{\bf{d}}}}| +({{{\bf{d}}}}\cdot {{{\bf{a}}}})| {{{\bf{c}}}}| }\right),\end{array}$$

(25)

where a = r_l − r_k, b = r_l − r_k+1, c = r_l+1 − r_k+1 and d = r_l+1 − r_k (ref. ⁶⁹).

Computing the writhe

The writhe has previously been used to study folding in protein systems⁷⁰ and supercoiling in DNA⁶⁸. In these studies, proteins and DNA strands are modelled as polymer chains made up of straight line segments. Similarly, we computed the writhe using⁶⁸

$$W{r}_{i}({{{{\rm{R}}}}}_{i})=\frac{1}{2\uppi }{\sum }_{k\ne l}{\omega }_{kl},$$

(26)

where ω_kl is the contribution to the writhe from the segments k and l on ring i, defined as⁶⁸

$$\begin{array}{rcl}{\omega }_{kl} & = & {{{\mathrm{sgn}}}}\left\{[({{{{\mathbf{r}}}}}_{l+1}-{{{{\mathbf{r}}}}}_{l})\times ({{{{\mathbf{r}}}}}_{k+1}-{{{{\mathbf{r}}}}}_{k})]\cdot {{{\bf{a}}}}\right\}\left({\sin }^{-1}({{{{\mathbf{n}}}}}_{1}\cdot {{{{\mathbf{n}}}}}_{2})+{\sin }^{-1}({{{{\mathbf{n}}}}}_{2}\cdot {{{{\mathbf{n}}}}}_{3})\right. \\&& + \left. {\sin }^{-1}({{{{\mathbf{n}}}}}_{3}\cdot {{{{\mathbf{n}}}}}_{4})+{\sin }^{-1}({{{{\mathbf{n}}}}}_{4}\cdot {{{{\mathbf{n}}}}}_{1})\right),\end{array}$$

(27)

where sgn(⋅) is the sign function and

$${{{{\mathbf{n}}}}}_{1}=\frac{{{{\bf{a}}}}\times {{{\bf{d}}}}}{| {{{\bf{a}}}}\times {{{\bf{d}}}}| },\quad {{{{\mathbf{n}}}}}_{2}=\frac{{{{\bf{d}}}}\times {{{\bf{c}}}}}{| {{{\bf{d}}}}\times {{{\bf{c}}}}| },\quad {{{{\mathbf{n}}}}}_{3}=\frac{{{{\bf{c}}}}\times {{{\bf{b}}}}}{| {{{\bf{c}}}}\times {{{\bf{b}}}}| },\quad {{{{\mathbf{n}}}}}_{4}=\frac{{{{\bf{b}}}}\times {{{\bf{a}}}}}{| {{{\bf{b}}}}\times {{{\bf{a}}}}| },$$

(28)

where a, b, c and d are defined as above.

Identifying knots

We made use of the freely available Python package ‘pyknotid’ to identify whether a ring (or a pair of rings sharing vertices) is knotted⁷¹. Using ‘pyknotid’, we computed the Gauss code for the ring, and following simplification by performing Reidemeister moves, we identified whether a knot was present. If present, the identity of the knot was determined using a knot look-up table, which includes information about all knots with up to 15 crossings. Only if the ring (or a pair of rings sharing vertices) was deemed to be knotted was the writhe then calculated.