Abstract
Existing experimental demonstrations of quantum computational advantage have had the limitation that verifying the correctness of the quantum device requires exponentially costly classical computations. Here we propose and analyse an interactive protocol for demonstrating quantum computational advantage, which is efficiently classically verifiable. Our protocol relies on a class of cryptographic tools called trapdoor claw-free functions. Although this type of function has been applied to quantum advantage protocols before, our protocol employs a surprising connection to Bell’s inequality to avoid the need for a demanding cryptographic property called the adaptive hardcore bit, while maintaining essentially no increase in the quantum circuit complexity and no extra assumptions. Leveraging the relaxed cryptographic requirements of the protocol, we present two trapdoor claw-free function constructions, based on Rabin’s function and the Diffie–Hellman problem, which have not been used in this context before. We also present two independent innovations that improve the efficiency of our implementation and can be applied to other quantum cryptographic protocols. First, we give a scheme to discard so-called garbage bits, removing the need for reversibility in the quantum circuits. Second, we show a natural way of performing postselection that reduces the fidelity needed to demonstrate quantum advantage. Combining these results, we describe a blueprint for implementing our protocol on Rydberg atom-based quantum devices, using hardware-native operations that have already been demonstrated experimentally.
Similar content being viewed by others
Main
The development of large-scale programmable quantum hardware has opened the door to testing a fundamental question in the theory of computation: can quantum computers outperform classical ones for certain tasks? This idea, termed quantum computational advantage, has motivated the design of novel algorithms and protocols to demonstrate advantage with minimal quantum resources, such as qubit number and gate depth1,2,3,4,5,6,7,8,9,10. Such protocols are naturally characterized along two axes: the computational speedup and the ease of verification. The former distinguishes whether a quantum algorithm exhibits a polynomial or super-polynomial speedup over the best known classical one. The latter classifies whether the correctness of the quantum computation is efficiently verifiable by a classical computer. Along these axes lie three broad paths to demonstrating advantage: (1) sampling from entangled quantum many-body wavefunctions, (2) solving a deterministic problem, for example prime factorization, via a quantum algorithm and (3) proving quantumness through interactive protocols.
Sampling-based protocols directly rely on the classical hardness of simulating quantum mechanics1,3,7,8,9,10. The ‘computational task’ is to prepare and measure a generic complex many-body wavefunction with little structure. As such, these protocols typically require minimal resources and can be implemented on near-term quantum devices11,12. The correctness of the sampling results, however, is exponentially difficult to verify. This has an important consequence: in the regime beyond the capability of classical computers, the sampling results cannot be explicitly checked, and quantum computational advantage can only be inferred (for example, extrapolated from simpler circuits).
Algorithms in the second class of protocols are naturally broken down by whether they exhibit polynomial or super-polynomial speedups. In the case of polynomial speedups, there are notable examples that are provably faster than any possible classical algorithm13,14. However, polynomial speedups are tremendously challenging to demonstrate in practice due to the slow growth of the separation between classical and quantum run-times, and overheads such as the time taken to read the input. Accordingly, the most attractive algorithms for demonstrating advantage tend to be those with a super-polynomial speedup, including Abelian hidden subgroup problems such as factoring and discrete logarithms15. The challenge is that, for all known protocols of this type, the quantum circuits required to demonstrate advantage are well beyond the capabilities of near-term experiments.
The final class of protocols demonstrates quantum advantage through an interactive proof16,17,18,19,20,21,22,23. At a high level, this type of protocol involves multiple rounds of communication between the classical verifier and the quantum prover; the prover must give self-consistent responses, despite not knowing what the verifier will ask next. This requirement of self-consistency rules out a broad range of classical cheating strategies and can imbue ‘hardness’ into questions that would otherwise be easy to answer. To this end, interactive protocols expand the space of computational problems that can be used to demonstrate quantum advantage. From a more pragmatic perspective, this can enable the realization of efficiently verifiable quantum advantage on near-term quantum hardware.
Recently, a beautiful interactive protocol was introduced that can operate both as a test for quantum advantage and as a generator of certifiable quantum randomness16. The core of the protocol is a two-to-one function, f, built on the computational problem known as ‘learning with errors’ (LWE)24. The demonstration of advantage leverages two important properties of the function. First, it is claw-free, meaning that it is computationally hard to find a pair of inputs (x0, x1) such that f(x0) = f(x1). Second, there exists a trapdoor: given some secret data t, it becomes possible to efficiently invert f and reveal the pair of inputs mapping to any output. (See Supplementary Information for an overview of trapdoor claw-free functions, TCFs.) However, to fully protect against cheating provers, the protocol requires a stronger version of the claw-free property called the adaptive hardcore bit; namely, for any input x0, which may be chosen by the prover, it is computationally hard to find even a single bit of information about x1 (specifically, the parity of any subset of the bits of x1). The need for an adaptive hardcore bit within this protocol severely restricts the class of functions that can operate as verifiable tests of quantum advantage.
In this Article we propose and analyse an interactive quantum advantage protocol that removes the need for an adaptive hardcore bit, with essentially zero overhead in the quantum circuit and no extra cryptographic assumptions. We present four main results. First, we demonstrate how an idea from tests of Bell’s inequality can serve the same cryptographic purpose as the adaptive hardcore bit25. In essence, our interactive protocol is a variant of the CHSH (Clauser, Horne, Shimony, Holt) game26, in which one player is replaced by a cryptographic construction. Normally, in CHSH, two quantum parties are asked to produce correlations that would be impossible for classical devices to produce. If space-like separation is enforced to rule out communication between the two parties, then the correlations constitute a proof of quantumness. In our case, the space-like separation is replaced by the computational hardness of a cryptographic problem. In particular, the quantum prover holds a qubit whose state depends on the cryptographic secret in the same way that the state of one CHSH player’s qubit depends on the secret measurement basis of the other player. An alternative interpretation, from the perspective of Bell’s theorem, is that the protocol can be thought of as a ‘single-detector Bell test’—the cryptographic task generates the same single-qubit state as would be produced by entangling a second qubit and measuring it with another detector. As in the CHSH game, a quantum device can pass the verifier’s test with a probability of ~85%, but a classical device can only succeed with probability of at most 75%. This finite gap in success probabilities is precisely what enables a verifiable test of quantum advantage.
Second, by removing the need for an adaptive hardcore bit, our protocol accepts a broader landscape of functions for interactive tests of quantum advantage (Table 1 and Methods). We contribute two constructions to this list. The first is based on the decisional Diffie–Hellman problem (DDH)27,28,29, and the second utilizes the function fN(x) = x2 mod N, where N is the product of two primes, which forms the backbone of the Rabin cryptosystem30,31. On the one hand, DDH is appealing because the elliptic-curve version of the problem is particularly hard for classical computers32,33,34. On the other hand, x2 mod N can be implemented substantially more efficiently, and its hardness is equivalent to factoring. We hope that these two constructions will provide a foundation for the search for more TCFs with desirable properties (small key size and efficient quantum circuits).
Third, we describe two innovations that facilitate our protocol’s use in practice: an inherent postselection scheme for increasing noisy devices’ probability of passing the test, and a way to substantially reduce overhead arising from the reversibility requirement of quantum circuits. The former allows quantum devices to trade off low quantum fidelities for a proportional increase in the overall runtime, while still passing the cryptographic test. The latter is a measurement-based uncomputation scheme specific to this protocol’s structure, which allows classical circuits to be converted into quantum ones with essentially zero overhead. We note that these constructions are probably applicable to other TCF-based quantum cryptography protocols as well, and thus may be of independent interest for tasks such as certifiable quantum random number generation.
Finally, focusing on the TCF x2 mod N, we provide explicit quantum circuits aimed at near-term quantum devices. We show that a verifiable test of quantum advantage can be achieved with ~103 qubits and a gate depth ~105 (a table of circuit sizes is provided in the Supplementary Information). We also co-design a specific implementation of x2 mod N optimized for a programmable Rydberg-based quantum computing platform. The native physical interaction corresponding to the Rydberg blockade mechanism enables the direct implementation of multi-qubit-controlled arbitrary phase rotations without the need to decompose such gates into universal two-qubit operations35,36,37,38,39. Access to such a native gate immediately reduces the gate depth for achieving quantum advantage by an order of magnitude.
Background and related work
The use of TCFs for quantum cryptographic tasks was pioneered in two recent breakthrough protocols: (1) giving classical homomorphic encryption for quantum circuits40 and (2) for generating cryptographically certifiable quantum randomness from an untrusted blackbox device16. The latter work also introduced the notion of an adaptive hardcore bit and serves as an efficiently verifiable test of quantum advantage. Remarkably, the scheme was further extended to allow a classical server to cryptographically verify the correctness of arbitrary quantum computations41, and it has also been applied to remote state preparation with implications for secure delegated computation42.
Recently, an improvement to the practicality of TCF-based proofs of quantumness was provided in the random oracle model (ROM)—a model of computation in which both the quantum prover and classical verifier can query a third-party ‘oracle’, which returns a random (but consistent) output for each input. In that work, the authors provide a protocol that both removes the need for the adaptive hardcore bit and also reduces the interaction to a single round17. Because the security of the protocol is proven in the ROM, implementing this protocol in practice requires applying the random oracle heuristic, in which the random oracle is replaced by a cryptographic hash function, but the hardness of classically defeating the protocol is taken to still hold. Only contrived cryptographic schemes have ever been broken by attacking the random oracle heuristic43,44, so it seems to be effective in practice, and the ROM protocol has substantial potential for use as a practical tool for benchmarking untrusted quantum servers. On the other hand, for a robust experimental test of the foundational complexity-theoretic claims of quantum computing—that quantum mechanics allows for algorithms that are superpolynomially faster than classical Turing machines—we desire the complexity-theoretic backing of the speedup to be as strong as possible (that is, provable in the ‘standard model’ of computation45), which is the goal pursued in the present work. With that said, we emphasize that the various optimizations described in the following—including the TCF families based on DDH and x2 mod N, as well as the schemes for postselection and discarding garbage bits—can be applied to the ROM protocol as well.
Finally, we also note two recent works that demonstrate that any TCF-based proof of quantumness, including the present work, can be implemented in constant quantum circuit depth (at the cost of more qubits)46,47.
Interactive protocol for quantum advantage
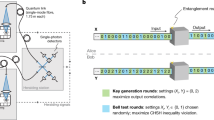
Our full protocol is shown diagrammatically in Fig. 1. It consists of three rounds of interaction between the prover and verifier (with a ‘round’ being a challenge from the verifier, followed by a response from the prover). The first round generates a multi-qubit superposition over two bitstrings that would be cryptographically hard to compute classically. The second round maps this superposition onto the state of one ancilla qubit, retaining enough information to ensure that the resulting single-qubit state is also hard to compute classically. The third round takes this single qubit as input to a CHSH-type measurement, allowing the prover to generate a bit of data that is correlated with the cryptographic secret in a way that would not be possible classically. Having described the intuition behind the protocol, we now lay out each round in detail.
In the first round of interaction, the classical verifier (right) selects a specific function from a trapdoor claw-free family and the quantum prover (left) evaluates it over a superposition of inputs. The goal of the second round is to condense the information contained in the prover’s superposition state onto a single ancilla qubit. The final round of interaction effectively performs a Bell inequality measurement, the outcome of which is cryptographically protected.
Description of the protocol
The goal of the first round is to generate a superposition over two colliding inputs to the TCF. It begins with the verifier choosing an instance fi of the TCF along with the associated trapdoor data t; fi is sent to the prover. As an example, in the case of x2 mod N, the ‘index’ i is the modulus N, and the trapdoor data are its factorization, p, q. The prover now initializes two registers of qubits, which we denote with the subscripts x and y. On these registers, they compute the entangled superposition \({\left|\psi \right\rangle }={\sum }_{x}{\left|x\right\rangle }_{{\mathsf{x}}}{\left|{f}_{i}{(x)}\right\rangle }_{{\mathsf{y}}}\), over all x in the domain of fi. The prover then measures the y register in the standard basis, collapsing the state to \({\left({\left|{x}_{0}\right\rangle }+{\left|{x}_{1}\right\rangle }\right)}_{{\mathsf{x}}}{\left|y\right\rangle }_{{\mathsf{y}}}\), with y = f(x0) = f(x1). The measured bitstring y is then sent to the verifier, who uses the secret trapdoor to compute x0 and x1 in full.
At this point, the verifier randomly chooses to either request a projective measurement of the x register, ending the protocol, or to continue with the second and third rounds. In the former case, the prover communicates the result of that measurement, yielding either x0 or x1, and the verifier checks that indeed f(x) = y. In the latter case, the protocol proceeds with the final two rounds.
The second round of interaction converts the many-qubit superposition \({\left|\psi \right\rangle }={\left|{x}_{0}\right\rangle }_{{\mathsf{x}}}+{\left|{x}_{1}\right\rangle }_{{\mathsf{x}}}\) into a single-qubit state \({\{{\left|0\right\rangle }_{{\mathsf{b}}},\,{\left|1\right\rangle }_{{\mathsf{b}}},\,{\left|+\right\rangle }_{{\mathsf{b}}},\,{\left|-\right\rangle }_{{\mathsf{b}}}\}}\) on an ancilla qubit b. The final state of b depends on the values of both x0 and x1. The round begins with the verifier choosing a random bitstring r of the same length as x0 and x1, and sending it to the prover. Using a series of CNOT gates from the x register to b, the prover computes the state \({\left|r\cdot {x}_{0}\right\rangle }_{{\mathsf{b}}}{\left|{x}_{0}\right\rangle }_{{\mathsf{x}}}+{\left|r\cdot {x}_{1}\right\rangle }_{{\mathsf{b}}}{\left|{x}_{1}\right\rangle }_{{\mathsf{x}}}\), where r ⋅ x denotes the binary inner product. Finally, the prover measures the x register in the Hadamard basis, storing the result as a bitstring d, which is sent to the verifier. This measurement disentangles x from b without collapsing the superposition of b. At the end of the second round, the prover’s state is \({(-1)}^{d\cdot {x}_{0}}{\left|r\cdot {x}_{0}\right\rangle }_{{\mathsf{b}}}+{(-1)}^{d\cdot {x}_{1}}{\left|r\cdot {x}_{1}\right\rangle }_{{\mathsf{b}}}\), which is one of \({\{{\left|0\right\rangle },\,{\left|1\right\rangle },\,{\left|+\right\rangle },\,{\left|-\right\rangle }\}}\). Crucially, it is cryptographically hard to predict whether this state is one of \({\{{\left|0\right\rangle },\,{\left|1\right\rangle }\}}\) or \({\{{\left|+\right\rangle },\,{\left|-\right\rangle }\}}\).
The final round of our protocol can be understood in analogy to the CHSH game26. Although the prover cannot extract the polarization axis from their single qubit (echoing the no-signalling property of CHSH), they can make a measurement that is correlated with it. This measurement outcome ultimately constitutes the proof of quantumness. In particular, the verifier requests a measurement in an intermediate basis, rotated from the Z axis around Y, by either θ = π/4 or −π/4. Because the measurement basis is never perpendicular to the state, there will always be one outcome that is more likely than the other (specifically, with probability cos2(π/8) ≈ 0.85). The verifier returns Accept if this ‘more likely’ outcome is the one received.
In the next section we prove that a quantum device can cause the verifier to return Accept with substantially higher probability than any classical prover. A full test of quantum advantage would consist of running the protocol many times, until it can be established with high statistical confidence that the device has exceeded the classical probability bound.
Completeness and soundness
We now provide two theorems regarding the completeness (the noise-free quantum success probability) and soundness (an upper bound on the classical success probability) of the protocol. The proofs of both theorems are presented in the Methods.
Recall that after the first round of the protocol, the verifier chooses to either request a standard basis measurement of the first register or to continue with the second and third rounds. In the theorems below, we consider the prover’s success probability across these two cases separately. We denote the probability that the verifier will accept the prover’s string x in the first case as px, and the probability that the verifier will accept the single-qubit measurement result in the second case as pCHSH.
Theorem 1: Completeness
An error-free quantum device honestly following the interactive protocol will cause the verifier to return Accept with px = 1 and pCHSH = cos2(π/8) ≈ 0.85.
Theorem 2: Soundness
Assume the function family used in the interactive protocol is claw-free. Then px and pCHSH for any classical prover must obey the relation
where ϵ is a negligible function of n, the length of the function family’s input strings.
The connection with the CHSH game is highlighted by the fact that if we let px = 1, the bound requires that pCHSH < 3/4 + ϵ(n) for a classical device, while pCHSH ≈ 0.85 for a quantum device, which matches the classical and quantum success probabilities of CHSH. In the Supplementary Information, we provide an example of a classical algorithm saturating the bound with px = 1 and pCHSH = 3/4.
Robustness and error mitigation via postselection
The existence of a finite gap between the classical and quantum success probabilities implies that our protocol can tolerate a certain amount of noise. A direct implementation of our interactive protocol on a noisy quantum device would require an overall fidelity of ~83% to exceed the classical bound (taking \({p}_{x}={{{\mathcal{F}}}}\) and \({p}_{{{{\rm{CHSH}}}}}={1/2}+{{{\mathcal{F}}}}/{2}\)). To allow devices with lower fidelities to demonstrate quantum advantage, our protocol allows for a natural tradeoff between fidelity and runtime, such that the classical bound can, in principle, be exceeded with only a small amount of coherence in the quantum device. This holds true even if the coherence is exponentially small in n; ultimately, the scheme is only limited by the runtime becoming excessive when the fidelity is extremely small.
The key idea is based on postselection. For most TCFs, there are many bitstrings of the correct length that are not valid outputs of f. Thus, if the prover detects such a y value in step 3 (Fig. 1), they can simply discard it and try again. In principle, the verifier can even use their trapdoor data to silently detect and discard iterations of the protocol with invalid y. This procedure does not leak data to a classical cheater, because the verifier does not communicate which runs were discarded. Because y is a function of x0 and x1, one might hope that this postselection scheme also rejects states where x0 or x1 has become corrupt. Although this may not always be the case, below we demonstrate numerically that this assumption holds for a specific implementation of x2 mod N. One could also compute a classical checksum of x0 and x1 before and after the main circuit to ensure that they have not changed during its execution. Assuming that such bit-flip errors are indeed rejected, the possibility remains of an error in the phase between \({\left|{x}_{0}\right\rangle}\) and \({\left|{x}_{1}\right\rangle}\). In the Supplementary Information we demonstrate that a prover holding the correct bitstrings but with an error in the phase can still saturate the classical bound; if the prover can avoid phase errors even a small fraction of the time, they will push past the classical threshold.
We numerically analyse the effectiveness of this postselection scheme for the specific TCF x2 mod N. To add redundancy to the outputs of the function, we map this TCF to the function (3ax)2mod(32aN), for a tunable integer a, and simulate the circuit under a generic noise model (see Methods for details). For a = 0, the circuit implements our original function x2 mod N, where, in the absence of postselection, an overall circuit fidelity of \({{{\mathcal{F}}}} \sim {0.83}\) is required to achieve quantum advantage. As depicted in Fig. 2a, even for a = 0, inherent redundancy in the TCF allows our postselection scheme to improve the advantage threshold down to \({{{\mathcal{F}}}} \sim {0.51}\). For a = 2, circuit fidelities with \({{{\mathcal{F}}}}\gtrsim {0.1}\) remain well above the quantum advantage threshold, while for a = 3 the required circuit fidelity drops below 1%. There is an extra runtime cost to performing the postselection, but, somewhat remarkably, an overhead of only 4.7× already enables quantum advantage to be achieved with an overall circuit fidelity of 10% (Fig. 2b). Crucially, this increase in runtime is overwhelmingly due to re-running the quantum circuit and does not imply the need for longer experimental coherence times.
Redundancy is added to the function x2 mod N by mapping it to (3ax)2mod(32aN). Numerical simulations are performed on a quantum circuit implementing the Karatsuba algorithm for a = {0, 1, 2, 3} (Supplementary Information). a, ‘Quantumness’ measured in terms of the classical bound from equation (1) as a function of the total circuit fidelity. With a = 3, even a quantum device with only 1% circuit fidelity can demonstrate quantum advantage. b, The increased runtime associated with the postselection scheme, which arises from a combination of slightly larger circuit sizes and the need to re-run the circuit multiple times. The latter is by far the dominant effect. Dashed lines are a theory prediction with no fit parameters. Symbols are the result of numerical simulations at n = 512 bits, and error bars depict 2σ uncertainty.
Quantum circuits for TCFs
Although all of the TCFs listed in Table 1 can be utilized within our interactive protocol, each has its own set of advantages and disadvantages. For example, the TCF based on the DDH (described in the Methods) already enables a demonstration of quantum advantage at a key size of 160 bits (with a hardness equivalent to 1,024-bit integer factorization34); however, building a circuit for this TCF requires a quantum implementation of Euclid’s algorithm, which is challenging48. We thus focus on designing quantum circuits implementing Rabin’s function, x2 mod N.
Quantum circuits for x 2 mod N
We explore four different circuits (see Supplementary Information for implementations of these algorithms in Python using the Cirq library). The first two are quantum implementations of the Karatsuba and ‘schoolbook’ classical integer multiplication algorithms (see Supplementary Information for details). Normally, quantum implementations of classical circuits have some overhead due to the need to make the gates reversible so as to be consistent with unitarity49,50,51,52,53. Our protocol exhibits the surprising property that it permits a measurement scheme to discard so-called ‘garbage bits’ that arise from these reversible gates, allowing classical circuits to be converted into quantum ones with essentially zero overhead (see Methods for details). This measurement scheme substantially reduces the cost of the schoolbook and Karatsuba circuits. The other two circuits, which we call the ‘phase circuits’, are intrinsically quantum algorithms: they use doubly controlled phase rotations to directly compute x2 mod N in the phases of a superposition state, and then transfer that phase to the computational basis via a quantum Fourier transform, as shown in Fig. 3. Naively this requires \({{{\mathcal{O}}}}({n}^{3})\) gates and \({2n}+{{{\mathcal{O}}}}{(1)}\) qubits; in the Methods we describe how to optimize this type of circuit for qubit number and gate count, respectively. A comparison of approximate gate counts and other resources for each of the four circuits is provided in Supplementary Table 1. The Karatsuba algorithm is the most efficient in terms of the total gates and circuit depth, and the phase circuits are most efficient in terms of qubit usage and measurement complexity.
n is the length of the input register and \({m}={n}+{{{\mathcal{O}}}}{(1)}\) is the length of the output register. This circuit can be modified to reduce both the gate and qubit count (see Methods for details).
Experimental implementation
Motivated by recent advances in the creation and control of many-body entanglement in programmable quantum systems11,54,55,56, we propose an experimental implementation of our interactive protocol based on neutral atoms coupled to Rydberg states36,39. Crucially, the so-called ‘Rydberg blockade’ interaction natively realizes the multi-qubit controlled phase rotations from which the ‘phase’ circuits described above are built. We envision a three-dimensional (3D) system of either alkali or alkaline-earth atoms trapped in an optical lattice or optical tweezer array [Fig. 4a)57,58,59. To be specific, we consider 87Rb with an effective qubit degree of freedom encoded in hyperfine states: \({\left|0\right\rangle }={\left|{F}={1},\,{m}_{{F}}={0}\right\rangle}\) and \({\left|1\right\rangle }={\left|{F}={2},\,{m}_{F}={0}\right\rangle}\). Gates between atoms are mediated by coupling to a highly excited Rydberg state \({\left|r\right\rangle}\), whose large polarizability leads to strong van der Waals interactions. This microscopic interaction enables the Rydberg blockade mechanism: when a single atom is driven to its Rydberg state, all other atoms within a blockade radius, Rb, become off-resonant from the drive, thereby suppressing their excitation (Fig. 4a,b)35.
a, Schematic of a 3D array of neutral atoms with Rydberg blockade interactions. The blockade radius can be considerably larger than the inter-atom spacing, enabling multi-qubit entangling operations. b, As an example, Rydberg atoms can be trapped in an optical tweezer array. The presence of an atom in a Rydberg excited state (red) shifts the energy levels of nearby atoms (blue), preventing the driving field (yellow arrow) from exciting them to their Rydberg state, \({\left|r\right\rangle}\). c, A single qubit phase rotation can be implemented by an off-resonant Rabi oscillation between one of the qubit states, for example, \({\left|1\right\rangle}\), and the Rydberg excited state. This imprints a tunable, geometric phase ϕ, which is determined by the detuning Δ and Rabi frequency Ω. d, Multi-qubit controlled phase rotations are implemented via a sequence of π pulses between the \({{\left|0\right\rangle }\leftrightarrow {\left|r\right\rangle}}\) transition of control atoms (yellow) and off-resonant Rabi oscillations on the target atoms (orange).
Somewhat remarkably, this blockade interaction enables the native implementation of all multi-qubit-controlled phase gates needed for our ‘phase’ circuits. In particular, consider the goal of applying a \({C}^{k}{R}_{\phi }^{\ell }\) gate; this gate applies phase rotations, {ϕ1, ϕ2, …, ϕℓ}, to target qubits {j1, j2, …, jℓ} if all k control qubits {i1, i2, …, ik} are in the \({\left|1\right\rangle}\) state (Fig. 4d). Experimentally, this can be implemented as follows: (1) sequentially apply (in any order) resonant π pulses on the \({{\left|0\right\rangle }\leftrightarrow {\left|r\right\rangle}}\) transition for the k desired control atoms, (2) off-resonantly drive the \({{\left|1\right\rangle }\leftrightarrow {\left|r\right\rangle}}\) transition of each target atom with detuning Δ and Rabi frequency Ω for a time duration \({T}={2\uppi }/{({{{\varOmega }}}^{2}+{{{\varDelta }}}^{2})}^{1/2}\) (Fig. 4c), (3) sequentially apply (in the opposite order as in (1)) resonant −π pulses (that is, π pulses with the opposite phase) to the k control atoms to bring them back to their original state. The intuition for why this experimental sequence implements the \({C}^{k}{R}_{\phi }^{\ell }\) gate is straightforward. The first step creates a blockade if any of the control qubits are in the \({\left|0\right\rangle}\) state, and the second step imprints a phase, \({\phi }={\uppi }{({1}-{{\varDelta }}/\sqrt{{{{\varDelta }}}^{2}+{{{\varOmega }}}^{2}})}\), on the \({\left|1\right\rangle}\) state, only in the absence of a blockade. Note that tuning the values of ϕi for each of the target qubits simply corresponds to adjusting the detuning and Rabi frequency of the off-resonant drive in the second step (Fig. 4c,d). In the Methods, we provide a detailed analysis of this protocol in the context of current-generation experiments, including a quantitative accounting of interaction strengths, geometry and decoherence.
Conclusion and outlook
The interplay between classical and quantum complexities ultimately determines the threshold for any quantum advantage scheme. In this Article we have proposed an interactive protocol for classically verifiable quantum advantage based on TCFs; in addition to proposing two TCFs (Table 1), we also provide explicit quantum circuits that leverage the microscopic interactions present in a Rydberg-based quantum computer. Our work allows near-term quantum devices to move one step closer toward a loophole-free demonstration of quantum advantage and also opens the door to a number of promising future directions.
First, our proof of soundness only applies to classical adversaries; whether it is possible to extend our protocol’s security to quantum adversaries remains an open question. A quantum-secure proof could enable our protocol’s use in a number of applications, such as certifiable random number generation16 and the verification of arbitrary quantum computations41. Second, our work motivates the search for new TCFs, which can be evaluated in the smallest possible quantum volume. Cryptographic primitives such as learning parity with noise (LPN), which are designed for use in low-power devices such as radio-frequency identification (RFID) cards, represent a promising path forward60. More broadly, one could also attempt to build modified protocols that simplify either the requirements for the cryptographic function or the interactions. Interestingly, recent work has demonstrated that using random oracles can remove the need for interactions in a TCF-based proof of quantumness17. Finally, although we have focused our experimental discussions on Rydberg atoms, a number of other platforms also exhibit features that facilitate the protocol’s implementation. For example, both trapped ions and cavity quantum electrodynamics systems can allow all-to-all connectivity, while superconducting qubits can be engineered to have biased noise61. This latter feature would allow noise to be concentrated into error modes detectable by our proposed postselection scheme.
Methods
Proof of ideal quantum success rate
Theorem 1: Completeness
An error-free quantum device honestly following the interactive protocol will cause the verifier to return Accept with px = 1 and pCHSH = cos2(π/8) ≈ 0.85.
Proof
If the verifier chooses to request a projective measurement of x after the first round, an honest quantum prover succeeds with probability px = 1 by inspection.
If the verifier chooses to instead perform the rest of the protocol, the prover will hold one of \({\{{\left|0\right\rangle },\,{\left|1\right\rangle },\,{\left|+\right\rangle },\,{\left|-\right\rangle }\}}\) after round 2. In either measurement basis the verifier may request in round 3, there will be one outcome that occurs with probability cos2(π/8), which is by construction the one the verifier accepts. Thus, an honest quantum prover has pCHSH = cos2(π/8) ≈ 0.85. □
Proof of classical success rate bound
Theorem 2: Soundness
Assume the function family used in the interactive protocol is claw-free. Then px and pCHSH for any classical prover must obey the relation
where ϵ is a negligible function of n, the length of the function family’s input strings.
Proof
We prove by contradiction. Assume that there exists a classical machine \({{{\mathcal{A}}}}\) for which px + 4pCHSH − 4 ≥ μ(n), for a non-negligible function μ. We show that there exists another algorithm \({{{\mathcal{B}}}}\) that uses \({{{\mathcal{A}}}}\) as a subroutine to find a pair of colliding inputs to the claw-free function, a contradiction.
Given a claw-free function instance fi, \({{{\mathcal{B}}}}\) acts as a simulated verifier for \({{{\mathcal{A}}}}\). \({{{\mathcal{B}}}}\) begins by supplying fi to \({{{\mathcal{A}}}}\), after which \({{{\mathcal{A}}}}\) returns a value y, completing the first round of interaction. \({{{\mathcal{B}}}}\) now chooses to request the projective measurement of the x register, and stores the result as x0. Letting \({p}_{{x}_{0}}\) be the probability that x0 is a valid preimage, by definition of px we have \({p}_{{x}_{0}}={p}_{x}\).
Next, \({{{\mathcal{B}}}}\) rewinds the execution of \({{{\mathcal{A}}}}\) to its state before x0 was requested. Crucially, rewinding is possible because \({{{\mathcal{A}}}}\) is a classical algorithm. \({{{\mathcal{B}}}}\) now proceeds by running \({{{\mathcal{A}}}}\) through the second and third rounds of the protocol for many different values of the bitstring r (Fig. 1), rewinding each time.
We now show that, for r selected uniformly at random, \({{{\mathcal{B}}}}\) can extract the value of the inner product r ⋅ x1 with probability \({p}_{r\cdot {x}_{1}}\ge {1}-{2}({1}-{p}_{{{{\rm{CHSH}}}}})\). \({{{\mathcal{B}}}}\) begins by sending r to \({{{\mathcal{A}}}}\), and receiving the bitstring d. \({{{\mathcal{B}}}}\) then requests the measurement result in both the θ = π/4 and θ = −π/4 bases, by rewinding in between. Supposing that both the received values are ‘correct’ (that is, would be accepted by the real verifier), they uniquely determine the single-qubit state \({\left|\psi \right\rangle }\in {\{{\left|0\right\rangle },\,{\left|1\right\rangle },\,{\left|+\right\rangle },\,{\left|-\right\rangle }\}}\) that would be held by an honest quantum prover. This state reveals whether r ⋅ x0 = r ⋅ x1, and, because \({{{\mathcal{B}}}}\) already holds x0, \({{{\mathcal{B}}}}\) can compute r ⋅ x1. We may define the probability (taken over all randomness except the choice of θ) that the prover returns an accepting value in the cases θ = π/4 and θ = −π/4 as pπ/4 and p−π/4, respectively. Then, via union bound, the probability that both are indeed correct is \({p}_{r\cdot {x}_{1}}\ge {1}-({1}-{p}_{\uppi /4})-({1}-{p}_{-\uppi /4})\). Considering that pCHSH = (pπ/4 + p−π/4)/2, we have \({p}_{r\cdot {x}_{1}}\ge {1}-{2}({1}-{p}_{{{{\rm{CHSH}}}}})\).
Now, we show that extracting r ⋅ x1 in this way allows x1 to be determined in full, even in the presence of noise, by rewinding many times and querying for specific (correlated) choices of r. In particular, the above construction is a noisy oracle to the encoding of x1 under the Hadamard code. By the Goldreich–Levin theorem62, list decoding applied to such an oracle will generate a polynomial-length list of candidates for x1. If the noise rate of the oracle is noticeably less than 1/2, x1 will be contained in that list; \({{{\mathcal{B}}}}\) can iterate through the candidates until it finds one for which f(x1) = y.
By Lemma 1 (below), for a particular iteration of the protocol, the probability that list decoding succeeds is bounded by \({p}_{{x}_{1}} > {2}{p}_{r\cdot {x}_{1}}-{1}-{2}{\mu }^{\prime}{(n)}\), for a noticeable function \({\mu }^{\prime}{(n)}\) of our choice. (Note that the oracle’s noise rate is not simply \({p}_{r\cdot {x}_{1}}\): that is the probability that any single value r ⋅ x1 is correct, but all of the queries to the oracle are correlated because they are for the same iteration of the protocol, and thus the same value of y.) Setting \({\mu }^{\prime}{(n)}={\mu }{(n)}/{4}\) and combining with the previous result yields \({p}_{{x}_{1}} > {1}-{4}({1}-{p}_{{{{\rm{CHSH}}}}})-{\mu }{(n)}/{2}\).
Finally, via union bound, the probability that \({{{\mathcal{B}}}}\) returns a claw is
and via the assumption that px + 4pCHSH − 4 > μ(n) we have
a contradiction. □
List decoding lemma
In this section we prove a bound on the probability that list decoding will succeed for a particular value of y, given an oracle’s noise rate over all values of y. Recall that by the Goldreich–Levin theorem62, list decoding of the Hadamard code is possible if the noise rate is noticeably less than 1/2.
Lemma 1
Consider a binary-valued function over two inputs g: Y × {0, 1}n → {0, 1}, and a noisy oracle \({{{\mathcal{G}}}}\) to that function. Assuming some distribution of values y ∈ Y and r ∈ {0, 1}n, define \({\epsilon }\equiv {\mathop{\Pr }\limits_{y,r}}{[{{{\mathcal{G}}}}({y},\,{r})\ne {g({y},\,{r})}]}\) as the ‘noise rate’ of the oracle. Now define the conditional noise rate for a particular y ∈ Y as
Then, the probability that ϵy is less than 1/2 − μ(n) for any positive function μ, over randomly selected y, is
Proof
Let S ⊆ Y be the set of y values for which ϵy < 1/2 − μ(n). Then by definition we have
Noting that we must have ϵy ≥ 1/2 − μ(n) for y ∉ S by definition, we may minimize the right-hand side of equation (5), yielding the bound
Rearranging this expression we arrive at pgood > 1 − 2ϵ − 2μ(n), which is what we desired to show. □
Numerical analysis of the postselection scheme for x 2 mod N
For the TCF f(x) = x2 mod N, we explicitly analyse the effectiveness of the postselection scheme. Let m be the length of the outputs of this function. In this case, ~1/4 of the bitstrings of length m are valid outputs, so one would naively expect to reject about 3/4 of corrupted bitstrings. By introducing additional redundancy into the outputs of f and thus increasing m, one can further decrease the probability that a corrupted y will incorrectly be accepted. Let us consider mapping x2 mod N to the function (kx)2modk2N for some integer k. This is particularly convenient because the prover can validate y by simply checking whether it is a multiple of k2. Moreover, the mapping adds only logk bits to the size of the problem, while rejecting a fraction 1 − 1/k2 of corrupted bitstrings.
We perform extensive numerical simulations demonstrating that postselection allows for quantum advantage to be achieved using noisy devices with low circuit fidelities (Fig. 2). We simulate quantum circuits for (kx)2modk2N at a problem size of n = 512 bits. Assuming a uniform gate fidelity across the circuit, we analyse the success rate of a quantum prover for k = 3a and a = {0, 1, 2, 3}. For these simulations we use our implementation of the Karatsuba algorithm, because it is the most efficient in terms of gate count and depth. The choice of k = 3a and details of the simulation are explained in the Supplementary Information.
Efficient quantum evaluation of irreversible classical circuits
The central computational step in our interactive protocol (that is, step 2 in Fig. 1) is for the prover to apply a unitary of the form
where fi(x) is a classical function and m is the length of the output register. This type of unitary operation is ubiquitous across quantum algorithms, and a common strategy for its implementation is to convert the gates of a classical circuit into quantum gates. Generically, this process induces substantial overhead in both time and space complexity due to the need to make the circuit reversible to preserve unitarity49,50. This reversibility is often achieved by using an additional register, g, of so-called ‘garbage bits’ and implementing \({{{{\mathcal{U}}}}}_{{f}_{i}}^{\prime}{\sum }_{x}{\left|x\right\rangle }_{{\mathsf{x}}}{\left|{0}^{\otimes m}\right\rangle }_{{\mathsf{y}}}{\left|{0}^{\otimes l}\right\rangle }_{{\mathsf{g}}}={\sum }_{x}{\left|x\right\rangle }_{{\mathsf{x}}}{\left|{f}_{i}{(x)}\right\rangle }_{{\mathsf{y}}}{\left|{g}_{i}{(x)}\right\rangle }_{{\mathsf{g}}}\). For each gate in the classical circuit, enough garbage bits are added to make the operation injective. In general, to maintain coherence, these bits cannot be discarded but must be ‘uncomputed’ later, adding substantial complexity to the circuits.
A particularly appealing feature of our protocol is the existence of a measurement scheme to discard garbage bits, allowing for the direct mapping of classical to quantum circuits with no overhead. Specifically, we envision the prover measuring the qubits of the g register in the Hadamard basis and storing the results as a bitstring h, yielding the state
The prover has avoided the need to do any uncomputation of the garbage bits, at the expense of introducing phase flips onto some elements of the superposition. These phase flips do not affect the protocol, as long as the verifier can determine them. Although classically computing h ⋅ gi(x) is efficient for any x, computing it for all terms in the superposition is infeasible for the verifier. However, our protocol provides a natural way around this. The verifier can wait until the prover has collapsed the superposition onto x0 and x1, before evaluating gi(x) only on those two inputs (this is true because gi(x) is the result of adding extra output bits to the gates of a classical circuit, which is efficient to evaluate on any input).
Crucially, the prover can measure away garbage qubits as soon as they would be discarded classically, instead of waiting until the computation has completed. If these qubits are then reused, the quantum circuit will use no more space than the classical one. This feature allows for substantial improvements in both gate depth and qubit number for practical implementations of the protocol (last rows of Supplementary Table 1). We note that performing many individual measurements on a subset of the qubits is difficult on some experimental systems, which may make this technique challenging to use in practice. However, recent hardware advances have demonstrated these ‘intermediate measurements’ in practice with high fidelity, for example by spatially shuttling trapped ions63,64. We thus expect that the capability to perform partial measurements will not be a barrier in the near term. This issue can also be mitigated somewhat by collecting ancilla qubits and measuring them in batches rather than one by one, allowing for a direct tradeoff between ancilla usage and the number of partial measurements.
TCF constructions
Here we present two TCF families for use in the protocol of this Article. These families are defined by three algorithms: Gen, a probabilistic algorithm that selects an index i specifying one function in the family and outputs the corresponding trapdoor data t; fi, the definition of the function itself; and T, a trapdoor algorithm that efficiently inverts fi for any i, given the corresponding trapdoor data t. Here we provide the definitions of the function families (proofs of their cryptographic properties are included in the Supplementary Information). In these definitions we use a security parameter λ following the notation of the cryptographic literature; λ is informally equivalent to the ‘problem size’ n defined in the main text as the length of the TCF input string.
TCF from Rabin’s function x 2 mod N
Rabin’s function fN(x) = x2 mod N, with N the product of two primes, was first used in the context of public-key cryptography and digital signatures30,31. We use it to define the TCF family \({{{{\mathcal{F}}}}}_{{{{\rm{Rabin}}}}}\), as follows.
Function generation
\({\mathsf{Gen}}{\left({1}^{\lambda }\right)}\)
-
1.
Randomly choose two prime numbers p and q of length λ/2 bits, with \({p}{{{\rm{mod}}}}{4}\equiv {q}{{{\rm{mod}}}}{4}\equiv {3}{{{\rm{mod}}}}{4}\).
-
2.
Return N = pq as the function index, and the tuple (p, q) as the trapdoor data.
(In practice, p and q must be selected with some care such that Fermat factorization and Pollard’s p − 1 algorithm65 cannot be used to efficiently factor N classically. Selecting p and q in the same manner as for RSA encryption would be effective66.)
Function definition
fN: [N/2] → [N] is defined as
The domain is restricted to [N/2] to remove extra trivial collisions of the form (x, −x).
Trapdoor
The trapdoor algorithm is the same as the decryption algorithm of the Rabin cryptosystem30. On input y and key (p, q), the Rabin decryption algorithm returns four integers (x0, x1, −x0, −x1) in the range [0, N). x0 and x1 can then be selected by choosing the two values that are smaller than N/2. A proof in the Supplementary Information provides an overview of the algorithm.
TCF from decisional Diffie–Hellman
We now present the TCF family \({{{{\mathcal{F}}}}}_{{{{\rm{DDH}}}}}\) based on the decisional DDH. DDH is defined for a multiplicative group \({\mathbb{G}}\); informally, the DDH assumption states that for a group generator g and two integers a and b, given g, ga and gb it is computationally hard to distinguish gab from a random group element. We expand on a known DDH-based trapdoor one-way function construction28,29, adding the claw-free property to construct a TCF.
Function generation
\({\mathsf{Gen}}{\left({1}^{\lambda }\right)}\)
-
1.
Choose a group \({\mathbb{G}}\) of order \({q} \sim {{{\mathcal{O}}}}{\left({2}^{\lambda }\right)}\), and a generator g for that group.
-
2.
For dimension k > log2q choose a random invertible matrix \({{{\bf{M}}}}\in {{\mathbb{Z}}}_{q}^{k\times k}\).
-
3.
Compute \({g}^{{{{\bf{M}}}}}={\left({g}^{{{{{\bf{M}}}}}_{ij}}\right)}\in {{\mathbb{G}}}^{k\times k}\) (element-wise exponentiation).
-
4.
Choose a secret vector \({{{\bf{s}}}}\in {\left\{0,\,1\right\}}^{k}\); compute the vector gMs (where Ms is the matrix-vector product, and again the exponentiation is element-wise).
-
5.
Publish the pair \({\left({g}^{{{{\bf{M}}}}},\,{g}^{{{{\bf{Ms}}}}}\right)}\), retain \({\left(g,\,{{{\bf{M}}}},\,{{{\bf{s}}}}\right)}\) as the trapdoor data.
Function definition
Let d be a power of two with \({d} \sim {{{\mathcal{O}}}}{\left({k}^{2}\right)}\). We define the function fi as fi(b∣∣x) ≔ fi, b(x), where ∣∣ denotes concatenation, for a pair of functions \({f}_{i,\,b}:{{\mathbb{Z}}}_{d}^{k}\to {{\mathbb{G}}}^{k}\):
Trapdoor
The algorithm takes as input the trapdoor data \({\left(g,\,{{{\bf{M}}}},\,{{{\bf{s}}}}\right)}\) and a value \({y}={g}^{{{{{\bf{Mx}}}}}_{0}}={g}^{{{{\bf{M}}}}{\left({{{{\bf{x}}}}}_{1}+{{{\bf{s}}}}\right)}}\), and returns the claw \({\left({{{{\bf{x}}}}}_{0},\,{{{{\bf{x}}}}}_{1}\right)}\):
T((g, M, s), y)
- 1.
Compute M−1 using M.
- 2.
Compute \({g}^{{{{{\bf{M}}}}}^{-1}{{{\bf{M}}}}{{\bf{x}}}_{0}}={g}^{{{{{\bf{x}}}}}_{0}}\).
- 3.
Take the discrete logarithm of each element of \({g}^{{{{{\bf{x}}}}}_{0}}\), yielding x0. Crucially, this is possible because the elements of x are in \({{\mathbb{Z}}}_{d}\) and \({d}={\mathsf{poly}}{\left(n\right)}\), so the discrete logarithm can be computed in polynomial time by brute force.
- 4.
Compute x1 = x0 − s.
- 5.
Return (x0, x1).
Phase circuits for x 2 mod N
Here we describe the two circuits, amenable to near-term quantum devices, that utilize quantum phase estimation to implement the function f(x) = x2 mod N. The intuition behind our approach is as follows: we will compute x2/N in the phase and transfer it to an output register via an inverse quantum Fourier transform67,68. The modulo operation occurs automatically as the phase wraps around the unit circle, avoiding the need for a separate reduction step.
To implement \({\sum }_{x}{\left|x\right\rangle }_{{\mathsf{x}}}{\left|{x}^{2}\ {{{\rm{mod}}}}\,{N}\right\rangle }_{{\mathsf{y}}}\), we design a circuit to compute
where H is a Hadamard gate, IQFT represents an inverse quantum Fourier transform, and w ≡ x2/N = 0. w1w2 ⋯ wm is an m-bit binary fraction with \({m} > {n}+{{{\mathcal{O}}}}{(1)}\) to sufficiently resolve the value x2 mod N in post-processing. Here, \({\tilde{{{{\mathcal{U}}}}}}_{{w}_{N}}\) is the diagonal unitary:
By performing a binary decomposition of the phase in equation (13):
one immediately finds that \({\tilde{{{{\mathcal{U}}}}}}_{{w}_{N}}\) is equivalent to applying a series of doubly-controlled phase rotation gates of angle
Here, the control qubits are i, j in the x register, and the target qubit is k in the y register. Crucially, the value of this phase for any i, j, k can be computed classically when the circuit is compiled.
As depicted in Supplementary Fig. 1, we propose two explicit circuits to implement \({\tilde{{{{\mathcal{U}}}}}}_{{w}_{N}}\), one optimizing for qubit count and the other for gate count. The first circuit (Supplementary Fig. 1a) takes advantage of the fact that the output register is measured immediately after it is computed; this allows one to replace the m output qubits with a single qubit that is measured and reused m times. Moreover, by replacing groups of doubly controlled gates with a Toffoli gate and a series of singly controlled gates, one ultimately arrives at an implementation that requires \({n}^{3}/{2}+{{{\mathcal{O}}}}({n}^{2})\) gates, but only \({n}+{{{\mathcal{O}}}}{(1)}\) qubits. We note that this does require individual measurement and reuse of qubits, which has been a challenge for experiments. Recent experiments, however, have demonstrated this capability63,64.
Our second circuit (Supplementary Fig. 1b), which optimizes for gate count, leverages the fact that ϕijk (equation (15)) only depends on i + j + k, allowing one to combine gates with a common sum. In this case, one can define ℓ = i + j and then, for each value of ℓ, simply ‘count’ the number of values of i, j for which both control qubits are 1. By then performing controlled gates off of the qubits of the counter register, one can reduce the total gate complexity by a factor of n/logn, leading to an implementation with \({2}{n}^{2}{\log }{n}+{{{\mathcal{O}}}}({n}^{2})\) gates.
Analysis of experimental details in Rydberg atom systems
Initial demonstrations of our protocol can already be implemented in current-generation Rydberg experiments, where a number of essential features have recently been shown, including (1) the coherent manipulation of individual qubits trapped in a 3D tweezer array57,58, (2) the deterministic loading of atoms in a 3D optical lattice59 and (3) fast entangling gate operations with fidelities F ≥ 0.974 (refs. 36,37,38). To estimate the number of entangling gates achievable within decoherence timescales, let us imagine choosing a Rydberg state with a principal quantum number n ≈ 70. This yields a strong van der Waals interaction \({V}{(\boldsymbol{r})}={C}_{6}/{r}^{6}\), where r is the displacement between the interacting atoms and the C6 coefficient is ~(2π) × 880 GHz μm6 (ref. 69). Combined with a coherent driving field of Rabi frequency Ω ≈ (2π) × 1–10 MHz, the van der Waals interaction can lead to a blockade radius of up to \({R}_{\rm{b}}={\left({C}_{6}/{{\varOmega }}\right)}^{1/6} \approx {10}\,{\upmu}{\rm{m}}\). Within this radius, one can arrange ~102 all-to-all interacting qubits, assuming an atom-to-atom spacing of a0 ≈ 2 μm. (We note that this spacing is ultimately limited by a combination of the optical diffraction limit and the orbital size of n ≈ 70 Rydberg states.) In current experiments, the decoherence associated with the Rydberg transition is typically limited by a combination of inhomogeneous Doppler shifts and laser phase/intensity noise, leading to 1/T2 ≈ 10–100 kHz (refs. 36,70,71). Taking everything together, one should be able to perform ~103 entangling gates before decoherence occurs (this is comparable to the number of two-qubit entangling gates possible in other state-of-the-art platforms11,72). Although this falls short of enabling an immediate full-scale demonstration of classically verifiable quantum advantage, we hasten to emphasize that the ability to directly perform multi-qubit entangling operations substantially reduces the cost of implementing our interactive protocol. For example, the standard decomposition of a Toffoli gate uses six CNOT gates and seven T and T† gates, with a gate depth of 12 (refs. 73,74,75); an equivalent three-qubit gate can be performed in a single step via the Rydberg blockade mechanism.
Data availability
No raw data were used in this study.
Code availability
The code used in this work (implementations of quantum circuits for x2 mod N and analysis of the effectiveness of the postselection scheme) is available on GitHub (https://github.com/GregDMeyer/quantum-advantage) and is also archived on Zenodo (https://zenodo.org/record/6519250)76.
References
Aaronson, S. & Arkhipov, A. The computational complexity of linear optics. In Proc. Forty-Third Annual ACM Symposium on Theory of Computing STOC’11 333–342 (ACM, 2011).
Farhi, E. & Harrow, A. W. Quantum supremacy through the quantum approximate optimization algorithm. Technical report MIT/CTP-4771. Preprint at https://arxiv.org/abs/1602.07674 (2016).
Bremner, M. J., Montanaro, A. & Shepherd, D. J. Average-case complexity versus approximate simulation of commuting quantum computations. Phys. Rev. Lett. 117, 080501 (2016).
Lund, A. P., Bremner, M. J. & Ralph, T. C. Quantum sampling problems, BosonSampling and quantum supremacy. npj Quantum Inf. 3, 15 (2017).
Harrow, A. W. & Montanaro, A. Quantum computational supremacy. Nature 549, 203–209 (2017).
Terhal, B. M. Quantum supremacy, here we come. Nat. Phys. 14, 530–531 (2018).
Boixo, S. et al. Characterizing quantum supremacy in near-term devices. Nat. Phys. 14, 595–600 (2018).
Bouland, A., Fefferman, B., Nirkhe, C. & Vazirani, U. On the complexity and verification of quantum random circuit sampling. Nat. Phys. 15, 159–163 (2019).
Aaronson, S. & Chen, L. Complexity-theoretic foundations of quantum supremacy experiments. In Proc. 32nd Computational Complexity Conference (CCC 2017) (ed. O’Donnell, R.) Vol. 79 of Leibniz International Proceedings in Informatics (LIPIcs) 22:1–22:67 (Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2017).
Neill, C. et al. A blueprint for demonstrating quantum supremacy with superconducting qubits. Science 360, 195–199 (2018).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Zhong, H.-S. et al. Quantum computational advantage using photons. Science 370, 1460–1463 (2020).
Bravyi, S., Gosset, D. & König, R. Quantum advantage with shallow circuits. Science 362, 308–311 (2018).
Bravyi, S., Gosset, D., König, R. & Tomamichel, M. Quantum advantage with noisy shallow circuits. Nat. Phys. 16, 1040–1045 (2020).
Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26, 1484–1509 (1997).
Zvika Brakerski, Paul Christiano, Urmila Mahadev, Umesh Vazirani, and Thomas Vidick. 2021. A Cryptographic Test of Quantumness and Certifiable Randomness from a Single Quantum Device. J. ACM 68, 5, Article 31 (October 2021), 47 pages. https://doi.org/10.1145/3441309
Brakerski, Z., Koppula, V., Vazirani, U. & Vidick, T. Simpler Proofs of Quantumness. in 15th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2020) (ed. Flammia, S. T.) 158 8:1–8:14 (Schloss Dagstuhl–Leibniz-Zentrum für Informatik, 2020).
Aharonov, D., Ben-Or, M., Eban, E. & Mahadev, U. Interactive proofs for quantum computations. Preprint at https://arxiv.org/abs/1704.04487 (2017).
Watrous, J. PSPACE Has Constant-Round Quantum Interactive Proof Systems. in Proceedings of the 40th Annual Symposium on Foundations of Computer Science 112 (IEEE Computer Society, 1999).
Kitaev, A. & Watrous, J. Parallelization, amplification and exponential time simulation of quantum interactive proof systems. In Proc. Thirty-Second Annual ACM Symposium on Theory of Computing 608–617 (ACM, 2000).
Kobayashi, H. & Matsumoto, K. Quantum multi-prover interactive proof systems with limited prior entanglement. J. Comput. Syst. Sci. 66, 429–450 (2003).
Fitzsimons, J. & Vidick, T. A multiprover interactive proof system for the local Hamiltonian problem. In Proc. 2015 Conference on Innovations in Theoretical Computer Science 103–112 (ACM, 2015).
Markov, I. L., Fatima, A., Isakov, S. V. & Boixo, S. Massively Parallel Approximate Simulation of Hard Quantum Circuits. in 2020 57th ACM/IEEE Design Automation Conference (DAC) 1–6 (2020). https://doi.org/10.1109/DAC18072.2020.9218591
Regev, O. On lattices, learning with errors, random linear codes and cryptography. In Proc. Thirty-Seventh Annual ACM Symposium on Theory of Computing STOC’05 84–93 (ACM, 2005).
Bell, J. S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1, 195–200 (1964).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Diffie, W. & Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 22, 644–654 (1976).
Peikert, C. & Waters, B. Lossy trapdoor functions and their applications. In Proc. Fortieth Annual ACM Symposium on Theory of Computing STOC’08 187–196 (ACM, 2008).
Freeman, D. M., Goldreich, O., Kiltz, E., Rosen, A. & Segev, G. More constructions of lossy and correlation-secure trapdoor functions. In Public Key Cryptography – PKC 2010 Lecture Notes in Computer Science (eds Nguyen, P. Q. & Pointcheval, D.) 279–295 (Springer, 2010).
Rabin, M. O. Digitalized Signatures and Public-Key Functions as Intractable as Factorization. Technical Report MIT/LCS/TR-212 (Massachusetts Institute of Technology, 1979).
Goldwasser, S., Micali, S. & R. L., R. A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17, 281–308 (1988).
Miller, V. Use of elliptic curves in cryptography. In Proc. Advances in Cryptology – CRYPTO ’85 Lecture Notes in Computer Science (ed. Williams, H. C.) 417–426 (Springer, 1986).
Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 48, 203–209 (1987).
Barker, E. Recommendation for Key Management Part 1: General. Technical Report No. NIST SP 800-57pt1r4 (National Institute of Standards and Technology, 2016).
Saffman, M. Quantum computing with atomic qubits and Rydberg interactions: progress and challenges. J. Phys. B 49, 202001 (2016).
Levine, H. et al. Parallel implementation of high-fidelity multiqubit gates with neutral atoms. Phys. Rev. Lett. 123, 170503 (2019).
Graham, T. et al. Rydberg-mediated entanglement in a two-dimensional neutral atom qubit array. Phys. Rev. Lett. 123, 230501 (2019).
I. S., M. et al. High-fidelity entanglement and detection of alkaline-earth Rydberg atoms. Nat. Phys. 16, 857–861 (2020).
Browaeys, A. & Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 16, 132–142 (2020).
Mahadev, U. Classical Homomorphic Encryption for Quantum Circuits. SIAM J. Comput. FOCS18-189 (2020) https://doi.org/10.1137/18M1231055
Mahadev, U. Classical Verification of Quantum Computations. In 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS) 259–267 (2018). https://doi.org/10.1109/FOCS.2018.00033
Gheorghiu, A. & Vidick, T. Computationally-Secure and Composable Remote State Preparation. In 2019 IEEE 60th Annual Symposium on Foundations of Computer Science (FOCS) 1024–1033 (2019). https://doi.org/10.1109/FOCS.2019.00066
Canetti, R., Goldreich, O. & Halevi, S. The Random Oracle Methodology, Revisited. Technical Report No. 011 (Association for Computing Machinery, 1998).
Koblitz, N. & A. J., M. The random oracle model: a twenty-year retrospective. Designs Codes Cryptogr. 77, 587–610 (2015).
Aaronson, S. & Chen, L. Complexity-Theoretic Foundations of Quantum Supremacy Experiments. In 32nd Computational Complexity Conference (CCC 2017) (ed. O’Donnell, R.) vol. 79 22:1–22:67 (Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2017).
Liu, Z. & Gheorghiu, A. Depth-efficient proofs of quantumness. Preprint at https://arxiv.org/abs/2107.02163 (2021).
Hirahara, S. & Le Gall, F. Test of Quantumness with Small-Depth Quantum Circuits. In 46th International Symposium on Mathematical Foundations of Computer Science (MFCS 2021) (eds. Bonchi, F. & Puglisi, S. J.) vol. 202 59:1–59:15 (Schloss Dagstuhl – Leibniz-Zentrum für Informatik, 2021).
Häner, T., Jaques, S., Naehrig, M., Roetteler, M. & Soeken, M. Improved Quantum Circuits for Elliptic Curve Discrete Logarithms. In Post-Quantum Cryptography (eds. Ding, J. & Tillich, J.-P.) 425–444 (Springer International Publishing, 2020). https://doi.org/10.1007/978-3-030-44223-1_23
C. H., B. Time/space trade-offs for reversible computation. SIAM J. Comput. 18, 766–776 (1989).
R. Y., L. & A. T., S. A note on Bennett’s time-space tradeoff for reversible computation. SIAM J. Comput. 19, 673–677 (1990).
Aharonov, D., Kitaev, A. & Nisan, N. Quantum circuits with mixed states. In Proc. Thirtieth Annual ACM Symposium on Theory of Computing 20–30 (ACM, 1998).
Babu, H. M. H., Islam, M. R., Chowdhury, S. M. A. & Chowdhury, A. R. Synthesis of full-adder circuit using reversible logic. In Proc. 17th International Conference on VLSI Design 757–760 (IEEE, 2004).
Kotiyal, S., Thapliyal, H. & Ranganathan, N. Circuit for reversible quantum multiplier based on binary tree optimizing ancilla and garbage bits. In 2014 27th International Conference on VLSI Design and 2014 13th International Conference on Embedded Systems 545–550 (IEEE, 2014).
Zhang, J. et al. Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator. Nature 551, 601–604 (2017).
Scholl, P. et al. Quantum simulation of 2D antiferromagnets with hundreds of Rydberg atoms. Nature 595, 233–238 (2021).
Ebadi, S. et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 595, 227–232 (2021).
Wang, Y., Zhang, X., T. A., C., Kumar, A. & D. S., W. Coherent addressing of individual neutral atoms in a 3D optical lattice. Phys. Rev. Lett. 115, 043003 (2015).
Wang, Y., Kumar, A., T.-Y., W. & D. S., W. Single-qubit gates based on targeted phase shifts in a 3D neutral atom array. Science 352, 1562–1565 (2016).
Kumar, A., T.-Y., W., Giraldo, F. & D. S., W. Sorting ultracold atoms in a three-dimensional optical lattice in a realization of Maxwell’s demon. Nature 561, 83–87 (2018).
Pietrzak, K. Cryptography from learning parity with noise. In SOFSEM 2012: Theory and Practice of Computer Science, Lecture Notes in Computer Science (eds Bieliková, M. et al.) 99–114 (Springer, 2012).
Puri, S. et al. Bias-preserving gates with stabilized cat qubits. Sci. Adv. 6, eaay5901 (2020).
Goldreich, O. & Levin, L. A. A hard-core predicate for all one-way functions. In Proc. Twenty First Annual ACM Symposium on Theory of Computing 25–32 (ACM, 1989).
Zhu, D. et al. Demonstration of interactive protocols for classically-verifiable quantum advantage. Bulletin of the American Physical Society https://meetings.aps.org/Meeting/DAMOP22/Session/Q07.2 (2021).
Ryan-Anderson, C. et al. Realization of real-time fault-tolerant quantum error correction. Phys. Rev. X 11, 041058 (2021).
J. M., P. Theorems on factorization and primality testing. Math. Proc. Camb. Philos. Soc. 76, 521–528 (1974).
R. L., R., Shamir, A. & Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21, 120–126 (1978).
Draper, T. G. Addition on a quantum computer. Preprint at https://arxiv.org/abs/quant-ph/0008033 (2000).
Beauregard, S. Circuit for Shor’s algorithm using 2n + 3 qubits. Preprint at https://arxiv.org/abs/quant-ph/0205095 (2003).
Löw, R. et al. An experimental and theoretical guide to strongly interacting Rydberg gases. J. Phys. B 45, 113001 (2012).
de Léséleuc, S., Barredo, D., Lienhard, V., Browaeys, A. & Lahaye, T. Analysis of imperfections in the coherent optical excitation of single atoms to Rydberg states. Phys. Rev. A 97, 053803 (2018).
Liu, Y. et al. Infidelity induced by ground-Rydberg decoherence of the control qubit in a two-qubit Rydberg-Blockade gate. Phys. Rev. Applied 15, 054020 (2021).
V. M., Schäfer et al. Fast quantum logic gates with trapped-ion qubits. Nature 555, 75–78 (2018).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge Univ. Press, 2011).
V. V., S. & I. L., M. On the CNOT-cost of TOFFOLI gates. Quantum Inf. Comput. 9, 461–486 (2009).
Barenco, A. et al. Elementary gates for quantum computation. Phys. Rev. A 52, 3457–3467 (1995).
Meyer, G. GregDMeyer/quantum-advantage: v1.1 (Zenodo, 2022); https://doi.org/10.5281/zenodo.6519250
Acknowledgements
We gratefully acknowledge the insights of and discussions with A. Bouland, S. Garg, A. Gheorghiu, Z. Landau, L. Lewis and T. Vidick. We are particularly indebted to J. Choi for insights about Rydberg-based quantum computing. This work was supported by the NSF QLCI programme (grant no. OMA-2016245), the Department of Defense (DOD; MURI grant no. FA9550-18-1-0161), and the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, under the Accelerated Research in Quantum Computing (ARQC) programme. N.Y.Y. acknowledges support from the David and Lucile Packard Foundation and a Google research award. G.D.K.M. acknowledges support from the DOD through the National Defense Science & Engineering Graduate Fellowship (NDSEG) Program. S.C. acknowledges support from the Miller Institute for Basic Research in Science.
Author information
Authors and Affiliations
Contributions
All authors contributed extensively to all aspects of this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks James Garrison and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kahanamoku-Meyer, G.D., Choi, S., Vazirani, U.V. et al. Classically verifiable quantum advantage from a computational Bell test. Nat. Phys. 18, 918–924 (2022). https://doi.org/10.1038/s41567-022-01643-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01643-7
This article is cited by
-
An elementary review on basic principles and developments of qubits for quantum computing
Nano Convergence (2024)
-
Post-quantum \(\kappa \)-to-1 trapdoor claw-free functions from extrapolated dihedral cosets
Quantum Information Processing (2024)
-
Interactive cryptographic proofs of quantumness using mid-circuit measurements
Nature Physics (2023)