Abstract
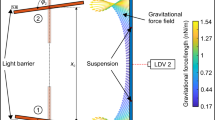
To date, there have been few dynamic measurements of gravitation in the laboratory, and fully controlled quantitative experiments have been limited to frequencies in the millihertz regime. Here we introduce a fully characterized experiment at frequencies in the hertz regime, which allows a quantitative determination of the dynamic gravitational interaction between two parallel beams vibrating at 42 Hz in bending motion. A large amplitude vibration of the transmitter beam produces a gravitationally induced motion of the high-quality-factor resonant detector beam with amplitudes up to 10−11 m. The sub-picometre-resolution measurement is made possible by a setup that combines acoustical, mechanical and electrical isolation; a temperature-stable environment; heterodyne laser interferometry; and lock-in detection. The interaction is quantitatively modelled based on Newton’s law of gravitation. Amplitude measurements at varying beam distances follow an inverse square law and agree with theoretical predictions to within approximately three percent. Furthermore, we extract the value of the gravitational constant G and near-field gravitational energy flow. We expect our experiment to enable progress in directions where current experimental evidence for dynamic gravitation is limited, such as the dynamic determination of G, inverse square law and gravitational shielding.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
Source data are provided with this paper. The data that support the findings of this study are available as an open access dataset37 or from the corresponding author upon reasonable request.
References
Newton, I., Cohen, I. B. & Whitman, A. The Principia: Mathematical Principles of Natural Philosophy (Univ. of California Press, 1999).
Einstein, A. Die grundlage der allgemeinen relativitätstheorie. Ann. Phys. 354, 769–822 (1916).
Speake, C. & Quinn, T. The search for Newton’s constant. Phys. Today 67, 27–33 (2014).
Gundlach, J. H. & Merkowitz, S. M. Measurement of Newton’s constant using a torsion balance with angular acceleration feedback. Phys. Rev. Lett. 85, 2869–2872 (2000).
Quinn, T., Parks, H., Speake, C. & Davis, R. Improved determination of G using two methods. Phys. Rev. Lett. 111, 101102 (2013).
Li, Q. et al. Measurements of the gravitational constant using two independent methods. Nature 560, 582–588 (2018).
Cavendish, H. XXI. Experiments to determine the density of the Earth. Philos. Trans. R. Soc. 88, 469–526 (1798).
Tiesinga, E., Mohr, P. J., Newell, D. B. & Taylor, B. N. CODATA recommended values of the fundamental physical constants: 2018. Rev. Mod. Phys. 93, 025010 (2021).
Adelberger, E. New tests of Einstein’s equivalence principle and Newton’s inverse-square law. Class. Quantum Gravity 18, 2397–2405 (2001).
Hoyle, C. D. et al. Submillimeter test of the gravitational inverse-square law: a search for ‘large’ extra dimensions. Phys. Rev. Lett. 86, 1418–1421 (2001).
Chiaverini, J., Smullin, S. J., Geraci, A. A., Weld, D. M. & Kapitulnik, A. New experimental constraints on non-Newtonian forces below 100 microns. Phys. Rev. Lett. 90, 151101 (2002).
Abbott, B. P. et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016).
Barish, B. C. Nobel lecture: LIGO and gravitational waves II. Rev. Mod. Phys. 90, 040502 (2018).
Chen, Y. T. & Cook, A. Gravitational Experiments in the Laboratory (Cambridge Univ. Press, 1993).
Westphal, T., Hepach, H., Pfaff, J. & Aspelmeyer, M. Measurement of gravitational coupling between millimetre-sized masses. Nature 591, 225–228 (2021).
Kapner, D. J. et al. Tests of the gravitational inverse-square law below the dark-energy length scale. Phys. Rev. Lett. 98, 021101 (2007).
Quinn, T. Don’t stop the quest to measure Big G. Nature 505, 455–455 (2014).
Pontikis, C. Détermination de la constant de gravitation par la méthode de résonance. C. R. Hebd. Seances Acad. Sci. Ser. B 274, 437–440 (1972).
Zahradnicek, J. Resonanz methode für die messung der gravitationsk constante mittels der drehwaage. Phys. Zeitschr. 34, 126–133 (1933).
Sinsky, J. A. Generation and detection of dynamic Newtonian gravitational fields at 1660 cps. Phys. Rev. 167, 1145–1151 (1968).
Hirakawa, H., Tsubono, K. & Oide, K. Dynamical test of the law of gravitation. Nature 283, 184–185 (1980).
Astone, P. et al. Experimental study of the dynamic Newtonian field with a cryogenic gravitational wave antenna. Eur. Phys. J. C 5, 651–664 (1998).
Long, J. C. et al. Upper limits to submillimetre-range forces from extra space-time dimensions. Nature 421, 922–925 (2003).
Liu, Y. et al. Gravitational forces between nonclassical mechanical oscillators. Phys. Rev. Appl. 15, 034004 (2021).
Schmöle, J. et al. A micromechanical proof-of-principle experiment for measuring the gravitational force of milligram masses. Class. Quantum Grav. 33, 125031 (2016).
Walker, W. D. Gravitational Interaction Studies. PhD thesis, ETH Zürich (1997).
Gordon, C. G. Generic vibration criteria for vibration-sensitive equipment. Proc. SPIE Optomech. Eng. Vib. Control 3786, 22–33 (1999).
Cremer, L., Heckl, M. & Petersson, B. A. T. Structure-Borne Sound: Structural Vibrations and Sound Radiation at Audio Frequencies (Springer, 2005).
Meirovitch, L. Fundamentals of Vibrations (McGraw-Hill Higher Education, 2001).
Hagedorn, P. & DasGupta, A. Vibrations and Waves in Continuous Mechanical Systems (Wiley, 2007).
Jackson, R. G. Novel Sensors and Sensing (CRC Press, 2004).
Zhang, J., Perez, R. J. & Lavernia, E. J. Documentation of damping capacity of metallic, ceramic and metal-matrix composite materials. J. Mater. Sci. 28, 2395–2404 (1993).
Robins, W. P. Phase Noise in Signal Sources: Theory and Applications (IET, 1984).
Efron, B. Bootstrap methods: another look at the jackknife. Ann. Stat. 7, 1–26 (1979).
Weichert, C. et al. A heterodyne interferometer with periodic nonlinearities smaller than ±10 pm. Meas. Sci. Technol. 23, 094005 (2012).
Pisani, M. et al. Comparison of the performance of the next generation of optical interferometers. Metrologia 49, 455–467 (2012).
Brack, T. Dataset for the article ‘Dynamic measurement of gravitational coupling between resonating beams in the Hertz regime’. ETHZ Research Collection https://doi.org/10.3929/ethz-b-000533207 (2022).
Acknowledgements
We gratefully acknowledge the support of ETH Zurich, maxon motor ag and ZC Ziegler Consultants AG. We received no specific funding for this work.
Author information
Authors and Affiliations
Contributions
T.B., B.Z., F.P., J.-C.T., S.B., D.S. and J.D. designed and constructed the experiment. T.B., B.Z. and J.D. conducted the experiments, T.B., F.B. and J.D. evaluated the data and analysed the results. T.B., S.K., J.F. and J.D. derived and evaluated the theory. All the authors wrote and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Andrei Metrikine and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Detector resonance frequency vs. temperature.
Detector beam resonance frequency f0 as a function of the mean temperature inside of the detector chamber. The points represent the SDOF fit result of the resonance frequency obtained from individual measurement runs (such as exemplarily shown in Fig. 3) at the mean temperature during the run (x - error bars = std). The y - error bars denote the 95% confidence interval of the SDOF fit result (not visible). The temperature of the air in the chamber and the beam’s material are assumed to be equal. A linear fit of all data points reveals a linear relation between the detector resonance frequency and its temperature with a coefficient of −0.01834(56) Hz/°C. The red shaded illustrates the 95% confidence band of the linear fit.
Source data
Source Data Fig. 3
Data for Fig. 3.
Source Data Fig. 4
Data for Fig. 4.
Source Data Fig. 5
Data for Fig. 5.
Source Data Extended Data Fig. 1
Data for Extended Data Fig. 1.
Rights and permissions
About this article
Cite this article
Brack, T., Zybach, B., Balabdaoui, F. et al. Dynamic measurement of gravitational coupling between resonating beams in the hertz regime. Nat. Phys. 18, 952–957 (2022). https://doi.org/10.1038/s41567-022-01642-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01642-8
This article is cited by
-
Dynamic gravitational excitation of structural resonances in the hertz regime using two rotating bars
Communications Physics (2023)
-
Good vibrations
Nature Physics (2022)
-
An unconventional strategy sizes up Newton’s ‘big G’
Nature (2022)