Abstract
Water drops moving on surfaces are not only an everyday phenomenon seen on windows but also form an essential part of many industrial processes. Previous understanding is that drop motion is dictated by viscous dissipation and activated dynamics at the contact line. Here we demonstrate that these two effects cannot fully explain the complex paths of sliding or impacting drops. To accurately determine the forces experienced by moving drops, we imaged their trajectory when sliding down a tilted surface, and applied the relevant equations of motion. We found that drop motion on low-permittivity substrates is substantially influenced by electrostatic forces. Our findings confirm that electrostatics must be taken into consideration for the description of the motion of water, aqueous electrolytes and ethylene glycol on hydrophobic surfaces. Our results are relevant for improving the control of drop motion in many applications, including printing, microfluidics, water management and triboelectric nanogenerators.
Similar content being viewed by others
Main
Water drops moving on surfaces are a common phenomenon. The lateral adhesion of drops can be a nuisance; for example, nature developed sophisticated surface structures to keep feathers, fur or plant leaves dry. Science and technology have adopted these surface modifications to keep drops from sticking on textiles, in microfluidics, or to keep window screens and glasses clear in the rain1,2,3,4. In other applications, the resistance of sessile drops to sliding motion is essential, for example, in coating, painting, flotation and deposition of insecticides and herbicides5,6. Still, a full description of forces acting on moving drops remains elusive. Closing this gap of knowledge has become more imperative due to the recent endeavour to generate electricity from moving drops7,8,9,10,11,12,13,14,15. This direct form of harvesting hydrovoltaic energy without moving parts promises to expand the range of hydroelectricity generation to small-scale devices applicable in remote and off-grid areas, or as emergency generators. The efficiency of energy conversion, however, is still too low. Here the poor understanding of moving drops still hampers the development of useful hydrovoltaic generators.
In accepted studies in the literature, drop motion is determined by viscous dissipation due to hydrodynamic flow in the drop and by activated processes, in which the contact line has to overcome local energy barriers leading to contact-line friction6,16,17,18,19,20,21,22. The viscous force of a sliding drop is commonly split in two components. Both are, to the first order, proportional to slide velocity U. One component comes from the viscous dissipation in the bulk, Fb, and the other from the wedge of the drop, Fw (refs. 23,24,25). Viscous dissipation in the wedge and contact-line friction change the macroscopically observed advancing and receding contact angles, namely, Θa(U) and Θr(U), respectively. As a result, the capillary force acting on a sliding drop4,26,27
depends on the velocity. Here w is the width of the contact area of the drop, γ is the surface tension of the liquid and k ≈ 1 is a geometrical factor that depends on the detailed shape of the drop24,27,28,29,30. Bulk viscous dissipation, which is much lower than viscous dissipation in the wedge, can be approximated by \(F_\mathrm{b} \approx \eta \frac{{\uppi lw}}{{2H}}U\) (Supplementary Section 1). Here η denotes the dynamic viscosity of the liquid, l is the length of the drop and H is its height.
Here by a simple tilted-plate experiment, we demonstrate that the motion of drops cannot be accurately predicted by these forces. In a tilted-plate experiment, a defined gravitational force Fg = mgsinα is acting in the lateral direction21,25,31,32,33,34,35,36. Here m is the mass of the drop, g = 9.81 m s–2 is the standard acceleration of gravity and α is the tilt angle.
Two observations demonstrate that the trajectories of the sliding drops require more than hydrodynamics and activated processes. First, on surfaces with identical surface chemistry but different substrate conductivities and substrate thicknesses, we see different average velocities. For example, in Fig. 1a–d, we show surfaces coated with perfluorooctadecyltrichlorosilane (PFOTS): a silicon wafer with ~2 nm oxide layer, a 1-mm-thick SiO2 plate and a 5-mm-thick SiO2 plate. The first drop on each surface had an average velocity of 0.25 m s–1 (Fig. 1a), 0.18 m s–1 (Fig. 1b) and 0.06 m s–1 (Fig. 1c), respectively. When substrate conductivity was higher than that in the wafer, we observed even faster drop motion. Gold surfaces coated with a monolayer of perfluorodecanethiol (Fig. 1e) and Teflon (Fig. 1f) films have surface chemistry comparable to PFOTS, yet with average velocities of 0.42 and 0.48 m s–1, respectively. Water drops move faster on these surfaces than on PFOTS-coated SiO2 surfaces. This simple experiment alone demonstrates that there is an important contribution missing in the description of drop motion.
Water drops (33 µl) sliding down a plate tilted by 50° after detaching from a grounded electrode and imaged every 10 ms with a side-view camera.
Our second piece of evidence is that for a series of drops, sliding speeds become dependent on the drop number and thus dependent on surface history. For example, the drop 50 sliding down a PFOTS-on-5-mm-SiO2 plate is faster than the drop 1 (Fig. 1d). The surface chemistries of the three samples mentioned are identical and thus one expects identical capillary and viscous forces; however, the sliding speed of the drops varied by more than a factor of two, both between samples and between successive drops.
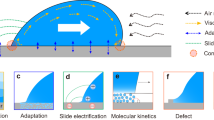
We believe that one logical explanation for this missing force is electrostatics. It is known that on bulk Teflon samples, fluorinated insulators and superhydrophobic surfaces, sliding water drops deposit negative electric charges, whereas the drops acquire a positive charge8,9,11,37,38,39,40,41,42. It is commonly believed that the surface charges behind sliding water drops are remnants of interfacial charges generated spontaneously at the water–solid interface8,11,37,43,44. Hydrophobic surfaces usually charge negatively in water. The reason for this charge is still debated45. The most popular explanation is an enrichment of hydroxyl ions at the interface. Alternative hypotheses speculate the origin of interfacial charge in the asymmetry of the hydrogen-bond network46, adsorption of bicarbonate/carbonate ions47 or the flow of electrons from water to the polymer15.
Surface charges generate an electric field in the air above the surface. A charge q on top of an infinitely extending dielectric half-space with a relative permittivity εS generates an electric field
Here, ε0 is the vacuum permittivity and r is the distance from the charge. If we now place a charged drop atop this charged surface, the drop will experience a Coulomb force that scales with 1/(1 + εS).
Given the importance of moving drops in our daily lives, we will address the following questions: is it possible to quantitatively measure electrostatic forces on moving drops? How? Can electrostatic forces explain the measured drop trajectories? Specifically, why and how does the substrate influence drop motion? Why is the motion of a drop influenced by previous drops? To answer these questions and to directly measure the forces acting on moving drops, we developed a new method to analyse tilted-plate experiments (Fig. 2a and Supplementary Section 2).
a, Schematic of the experimental setup (Supplementary Section 2). b, Hydrophobic samples under investigation. The ‘static’ advancing and receding contact angles \({{\Theta }}_\mathrm{a}^0\) and \({{\Theta }}_\mathrm{r}^0\) were measured with sessile water drops as they slowly inflated and deflated, and imaged in the side view (Supplementary Section 3). The errors arise due to repeated measurements on different positions and samples.
We prepared smooth, hydrophobic surfaces with receding and advancing contact angles ranging within 77–110° and 93–122°, respectively (Fig. 2b and Supplementary Section 3). All the surfaces had a root-mean-squared roughness of ≤1 nm, as determined by scanning force microscopy (SFM; Supplementary Section 4). To find out how strong the electrostatic forces are, we varied the substrate and its thickness d with respect to a grounded metal back-electrode. We chose SiO2 plates (εS = 3.7; Supplementary Section 5) as a low-permittivity substrate and Si wafers with only a natural oxide layer as a high-permittivity sample (εS = 11.7; data from the supplier, Silicon Materials). The stability of the coatings was confirmed by measuring the drop velocity, advancing and receding contact angles, and morphology before and after 1,000 water drops sliding down the reference surfaces. None of the parameters had changed (Supplementary Section 6). In the presence of the grounded metal back-electrode, the field is screened by image charges. The distance to the grounded metal layer defines the screening length.
To describe the results and analysis, we first concentrate on PFOTS-coated samples (Fig. 3a and Supplementary Section 7). For the PFOTS-on-Si sample, the first, second and subsequent drops showed similar velocity profiles (Fig. 3a, green symbols). In contrast to common expectation, on 1-mm- and 5-mm-thick SiO2 substrates (Fig. 3a, blue and red symbols), the velocity profiles of the first, second and subsequent drops were distinctly different, although all the samples have similar contact angles. First, the velocities tended to be lower on SiO2 than the silicon wafer. Second, often, rather complex traces occurred. Although complex, these traces are systematic and reproducible. For example, on the PFOTS-on-5-mm-SiO2 sample, the first drop shows a monotonically increasing velocity (Fig. 3a, red squares). However, for drop number 100 (Fig. 3a, red stars), the velocity increased for the first 3 cm, but then decreased again.
a, Velocity versus slide length for PFOTS-on-Si (green symbols), 1 mm SiO2 (blue) and 5 mm SiO2 (red) sliding down at an inclination of α = 50°. Supplementary Section 7 provides data for other tilt angles. b, Reference forces measured on four PFOTS-on-Si samples. Fitting the results for U ≤ 0.4 m s–1 (grey lines) led to Fr = 156 µN + (218 µN s m–1)U. c, Extra forces acting on the 1st, 2nd, 5th, 10th, 20th and 100th drop sliding down 50°-tilted PFOTS-on-5-mm-SiO2 sample at 1.3 s intervals. Intervals greater than 1 s were chosen to ensure that an adsorbed water film or nanodroplets behind a drop had time to equilibrate with the vapour phase. Forces were calculated with equation (3) with the PFOTS-on-Si sample as the reference. d, Measured drop charge versus drop number on PFOTS-coated samples. The results were measured at 50° tilt, 1.5 s intervals between the deionized water drops of 45 µl volume after 4 cm slide length. The lines are guides for the eye. Supplementary Section 12 provides additional details.
We draw two conclusions. First, the drop motion is not simply determined by viscous dissipation and activated dynamics at the contact line. Second, there is a fundamental difference between static and dynamic wetting. The static shape of a drop is largely determined by the properties of the top-most 1 nm of the surface; the substrate underneath has little influence (except in the case of strong externally applied electric fields such as in electrowetting48). In contrast, the dynamic properties such as the sliding speed are influenced by the substrate down to a thickness of the order of 1 mm.
To quantify the extra force, we analyse the equation of the motion of a drop:
In the acceleration term (\(m^ \ast \frac{{\mathrm{d}U}}{{\mathrm{d}t}}\)), we take into account the rolling components in drop motion6,16,21,36,49,50. Therefore, we used the effective mass \(m^ \ast\), which was determined by the direct numerical diffuse-interface simulations of the flow pattern inside sliding drops (Supplementary Section 8). These simulations gave an estimate of \(m^\ast/m=1.05\) as a good mean value for the velocity range covered by our experiments.
All the forces acting on the drop in the absence of electrostatic effects are summarized in the reference force, Fr(U). The reference force depends on the velocity U but not on the slide length L, because the surfaces are homogeneous. For the extra force Fe, the subscript ‘e’ indicates ‘extra’ or presumably ‘electrostatic’. It may depend on the velocity, slide length and drop number n.
To obtain the reference force, we assume that on Si wafers, electrostatic forces are negligible. This assumption is in line with the fact that no differences in velocity were observed between successive drops (Fig. 3a). With equation (3), we obtain \(F_\mathrm{r} = mg\sin \alpha - m^ \ast \frac{{\mathrm{d}U}}{{\mathrm{d}t}}\). The acceleration is obtained from the measured velocity traces, U(t). The reference forces increase linearly in the velocity range up to 0.4 m s–1 (Fig. 3b). This increase is correlated with an increase in length and decrease in width of the drops (Supplementary Section 9).
By inserting the respective drop widths as well as the advancing and receding contact angles into equation (1), we calculated the capillary force with k = 1 (Supplementary Fig. 9, red symbols). The capillary forces, which include wedge viscous forces (Supplementary Section 1), make up for most of the measured reference forces (Supplementary Fig. 9, black symbols). The bulk viscous forces (Supplementary Fig. 9, blue symbols) contribute less than 10% to the reference force (Supplementary Section 10).
With the reference force Fr(U) obtained from the experiments on Si wafers, we use U(t) curves measured on SiO2 to calculate the extra force using equation (3) as \(F_\mathrm{e}^n = mg\sin \alpha - m^ \ast \frac{{\mathrm{d}U}}{{\mathrm{d}t}} - F_\mathrm{r}\) (Fig. 3c and Supplementary Section 11). These extra forces are substantial, they depend on the drop number, n and they show complex distance dependency. Usually, the first and second drops experienced a strong force of 60–100 µN (up to 50% of the reference force), which then decayed over the observation range of 4 cm. The force is positive, hindering the drop motion. After around five drops, the initially high, decaying force gradually changed to an initially low, increasing extra force. Drop 100 showed almost an inverted profile of drop 1: starting at around 30 µN, it typically increased to 60 µN after 4 cm slide length.
To determine the origin of the extra force, we measured the drop charges (Supplementary Section 12). In agreement with earlier results39, on SiO2 substrates, the drops gained a positive charge and left behind a negative surface charge. For the first drop, the charge was typically Q1 = 1.0–1.5 nC on 1 mm and 5 mm SiO2 (Fig. 3d and Supplementary Table 2). It decreased with subsequent drops until it reached a saturation value of the order of 0.4 nC. In contrast, on silicon wafers, the drop charges were typically 5–10 times lower. We used these values of drop charges to model the electrostatic force.
Modelling the electrostatic force allowed us to explain the shapes and magnitudes of the measured extra force. We derive the electric field by integrating the field strength (equation (2)) for the surface charge density σn(x). We then multiply it with the drop charge Qn(x) to obtain the electrostatic force of the nth of drop:
Here, x is a coordinate along the path of the drop itself and the path of previous drops. The first integral represents the interaction of the drop with surface charges behind the drop. The second integral represents the interaction with charges deposited by previous drops ahead of the current drop (Supplementary Section 13). The parameter a characterizes the centre position of the charge of the drop; it is the horizontal distance to the rear rim (Supplementary Section 13 and Supplementary Fig. 13). Its value was obtained from numerical calculations of the electric-field distribution and electrostatic force (Supplementary Section 13).
We use a previously derived model to obtain plausible expressions for σn(x) and Qn(x) (ref. 39). Briefly, surface charges behind a sliding drop are the remnants of interfacial charges spontaneously generated at the water–solid interface8,11,37,43 (Fig. 4a). Hydrophobic surfaces usually charge negatively in water, probably by the adsorption of hydroxyl ions. Some of these charges fail to neutralize at the rear of the sliding drop and remain on the surface. As a result, the drop becomes positively charged. However, the transfer of charges to the solid–air surface decreases with an increasing drop potential39. As a result, the density of the deposited surface charges decreases with distance: σ1 = σ0e–x/λ. Here σ0 is the initial surface charge density and λ is the decay length (Supplementary Section 14). In addition, we allow the neutralization of surface charges with time. It is not yet clear which processes dominate surface neutralization, for example, flow of electrons through the grounded substrate or via the surface, ions in the air, or the ejection of electrons8,42. Neutralization is characterized by an exponential process with a relaxation time constant τ of typically 10 s. Based on the independent parameters σ0, λ and τ (Supplementary Section 12 and Supplementary Table 2), the surface charge density can be written as a function of the position and drop number.
a, Model applied to calculate the electrostatic forces versus slide length for a series of drops. Step (1): surface charges are generated when water comes into contact with the surface at the front of the drop, for example, by the adsorption of OH–, leaving H3O+ in the solution. Step (2): at the rear side of the drop, most surface charges are neutralized, for example, by the desorption of OH–. A fraction of the surface charges, however, transfers to the solid–air interface. Step (3): charges are neutralized. b, Calculated electrostatic force acting on the first drop (red line; equation (14) in the Supplementary Information) and after a large number of drops (blue line; equation (21) in the Supplementary Information). For comparison, we plotted the experimental results (symbols) for the 1st and 100th drop sliding down the PFOTS-on-5-mm-SiO2 sample (Fig. 3c). The parameters were chosen as determined from the measurements of drop charges (Supplementary Table 2; σ0 = 2 × 10–5 µC m–2, λ = 1.5 cm, τ = 7 s), the experimental conditions (w = 4 mm, l = 5 mm, Δt = 1.3 s, Lend = 6 cm), and the numerical computations for 5-mm-thick substrates (a = 1 mm = 0.2l; Supplementary Section 14).
Using equation (4), we obtain an analytical expression for the electrostatic force on the first drop (equation (14) in the Supplementary Information) and for higher drop numbers (n → ∞; equation (21) in the Supplementary Information). The calculated electrostatic force yields the same order of magnitude as the experimental results (Fig. 4b), and it explains the observed flip in the slope of Fe versus L curves when going from the first to subsequent drops with n ≥ 10.
All the drops start with zero charge and thus zero electrostatic force. The first drop deposits a negative charge on the neutral surface and acquires a positive charge within a distance of L ≈ λ (Fig. 4b, top-left schematic). The increase in drop and surface charges leads to a steep increase in the retarding electrostatic force, with a peak at L ≈ 0.8λ. As a result of drop charging, the drop potential increases, which hinders further charge deposition, and the drop charge saturates. As the drop reaches saturation and moves further from the strongly charged region of the surface, the retarding electrostatic force decreases (Fig. 4b, bottom-right schematic).
The maximum value predicted by the analytical solution at the beginning was missing in the experiments (Fig. 4b, red symbols). This could be the effect of an additional negative surface charge deposited right after the drop impacts the surface before touching the first grounded electrode. As a result, the maximum value would be outside our observation range. It was observed on other substrates described below.
For higher drop numbers (Fig. 4b, blue line, and Supplementary Fig. 15), the electrostatic retardation increases with slide distance because of two effects. First, the surface charge density is already high from previous drops. As a result, the drop needs to cover a larger distance to reach its saturation charge (Fig. 4b, top-right schematic). Thus, the increase in force (for the first drop, it happens in the first 1 cm) is stretched to a distance of ≥4 cm. Second, the surface charges in front of the drop that are left behind by previous drops lead to an acceleration. At the end of the path, the electrostatic force increases even more steeply because there are no more attractive charges ahead since the sample ends.
The good agreement between experiment and electrostatic theory indicates that on PFOTS-coated insulators, the extra forces are predominantly caused by electrostatic charging. To find out how ubiquitous electrostatic forces are, we performed experiments on other hydrophobic samples. When using conductive substrates or high-permittivity substrates (polystyrene (PS)-on-gold, Teflon-on-gold, polydimethylsiloxane (PDMS)-on-Si and thiols-on-gold substrates), the first, second and subsequent drops showed similar velocity profiles (Supplementary Section 15 and Supplementary Fig. 18). Thus, electrostatic effects are negligible. In contrast, on 1-mm- and 5-mm-thick SiO2 coated with PS, Teflon or PDMS, the velocity profiles of the first, second and subsequent drops were distinctly different (Supplementary Section 15 and Supplementary Fig. 19). This observation indicates that drop motion is substantially influenced by electrostatic forces. The charging of drops was detected on all the hydrophobic surfaces on SiO2 (Supplementary Section 12 and Supplementary Fig. 12). In contrast, for the PS-on-gold, Teflon-on-gold and PDMS-on-Si samples, charging was at least ten times lower.
A complex variety of \(F_\mathrm{e}^n\) versus L graphs were observed, depending on the drop number, tilt angle and substrate thickness. Two typical examples are plotted in Fig. 5; a full set of results is shown in Supplementary Sections 16 and 17. On several samples, such as the Teflon-on-1-mm-SiO2 sample, we observed the maximum in the force versus slide length curves predicted by the electrostatic theory for the first drop (Fig. 5a). We assume that a slight increase in decay length (λ) shifts the maximum value into our observation window. The charge measurements confirmed that indeed on Teflon, λ = 2.5 cm (compared with λ = 1.5 cm on PFOTS; Supplementary Table 2). For higher drop numbers, the maximum value became weaker and for drop numbers n ≥ 10, an increasing extra force started to dominate at larger slide lengths, in agreement with equation (21) in the Supplementary Information.
a, Teflon-on-1-mm-SiO2 sample at 35° tilt. b, PS-on-5-mm-SiO2 sample at 30° tilt. The results are plotted for the 1st, 2nd, 5th, 10th, 20th and 100th drop. Extra forces were calculated with equation (3), and Fr = 48 µN + (175 µN s m–1)U obtained with the Teflon-on-gold sample and Fr = 74 µN + (398 µN s m–1)U measured on the PS-on-gold sample as reference forces (Supplementary Fig. 20).
Figure 5a, however, also shows the limits of the simple model. It does not predict the minimum value in the electrostatic force for n ≥ 10 at shorter slide lengths. This deficit could be related to the assumption that charge deposition is independent of the slide velocity. Since the deposition of charges is a non-equilibrium process, it most likely depends on the velocity. At a low velocity, charge deposition is probably less pronounced than assumed. A velocity dependence of charge deposition is most likely also the reason for the oscillating electrostatic forces observed, for example, on the PS-on-5-mm-SiO2 sample (Fig. 5b). The oscillation period was not related to drop vibrations, which were at 50 Hz or faster. Thus, a future refinement of the description of charge deposition needs to include the velocity of the receding contact line.
Electrostatic retardation is not restricted to pure water. In aqueous drops containing 0.1–1,000.0 mM NaCl, electrostatic forces made up to 50% of the total force when sliding down the PFOTS-on-1-mm-SiO2 sample (Supplementary Section 18 and Supplementary Fig. 24). For drops of ethylene glycol (εS = 37, γ = 0.048 N m–1, η = 0.016 Pa s, V = 18.6 µl) on the Teflon-on-1-mm-SiO2 sample, the electrostatic forces for the first and second drops were of the order of 100 µN; they were even stronger than those for water despite the high viscosity and slow motion of drops (Supplementary Section 18 and Supplementary Fig. 25).
One additional consequence of electrostatic retardation is that impacting drops rebound differently depending on the conductivity and permittivity of the substrates. For example, 20 µl water drops falling from a height of 2.5 cm fully rebound from the Teflon-on-gold substrate. In contrast, the same drops stick on the Teflon-on-SiO2 substrate (Supplementary Section 19). When tilting the surface by 10°, drops rebound on the Teflon-on-gold substrate and roll off completely. On SiO2, drops do not rebound but split apart and stick to the surface. In particular, in printing and coating applications, for the production of window screens and glasses or in heat exchangers, this variation in electrostatic force may control whether impacting drops rebound from or stick to a surface. In general, the insight that surface permittivity influences drop motion opens new avenues towards engineering surfaces with desired wetting properties.
Methods
Tilted-plate experiments
To measure the forces acting on sliding drops, 33 µl drops of distilled water (<1 µS cm–1; Gibco, Thermo Fisher Scientific), 1 M NaCl solution (Carl Roth), 0.1 mM NaCl solution (made from 10 µl M NaCl solution and 100 ml distilled water) and ethylene glycol (99.8%; Sigma-Aldrich) were deposited at intervals of 1.3 s at the top of a tilted sample by a grounded syringe needle (1.5 mm outer diameter, Dosiernadel Vollmetal), which was connected to a peristaltic pump (MINIPULS 3, Gilson) (Supplementary Fig. 1). Before every series of drops, the surfaces were neutralized by an ionizing air blower for 10 min (Aerostat PC ionizing air blower, Simco-Ion). The drops fell ~5 mm, just enough so that they detached from the syringe before touching the surface. To make sure the drops start sliding without any initial charge, they were neutralized by a 0.025-mm-diameter grounded tungsten wire, right after they landed on the surface. The position where the drops detach from the grounded wire corresponds to the zero slide length (L = 0). The observation range starts where the full drop has detached from the grounded wire and the wire is not in the image anymore, that is, at L = 0.5 cm. Then, we imaged the drop with a frame rate of 1,000 frames per second in the side and front views over a length of typically 4.5 cm with a high-speed camera (FASTCAM Mini UX100 (Photron) with a TitanTL telecentric lens, ×0.268, one inch, C-mount (Edmund Optics)). By applying two parallel mirrors (25 × 36 mm2 protected silver mirror; PFR10-P01, Thorlabs) on both sides of the sample to guide the backlight from the telecentric backlight illuminator (138 mm; Edmund Optics), we also imaged the front view of the sliding drops at the same time. After typically Lend = 6 cm, the rim of the sample was reached and the drops fell off. To access a wide velocity range, we varied the tilt angle (Supplementary Fig. 6a). On longer samples, we verified that after a slide length of ~10–15 cm, the drops reach a steady-state velocity (Supplementary Fig. 6b). From video images, we extract slide length L, drop velocity U, contact angles at the front (advancing contact angle, Θa) and rear (receding contact angle, Θr), and length and width of the drop. All the parameters vary with time and thus with position. To extract Θa(U) and Θr(U) from the videos, we adapted the open drop-shape analysis from MATLAB (DSAfM) version 9.5.0.944444 (R2018b). The dynamic contact angles were determined by applying a polynomial fit to every contour image (Supplementary Section 2). All the measurements were conducted at a temperature of 20 ± 1 °C and a humidity of 15–30%.
Sample preparation
Five types of surface were prepared. (1) PFOTS monolayers on Si wafer, 1-mm-thick and 5-mm-thick SiO2 slides were prepared by chemical vapour deposition. After O2-plasma cleaning at 300 W for 10 min (Femto low-pressure plasma system, Diener electronic), the Si wafer (native oxide layer of 1.6 ± 0.3 nm as measured by ellipsometry; resistivity, <0.005 Ω cm; thickness, 525 ± 25 µm; Silicon Materials) and the SiO2 slides were placed in a vacuum desiccator containing a vial with 0.5 ml 1H,1H,2H,2H-perfluorooctadecyltrichlorosilane (97%; Sigma-Aldrich). We used 1-mm-thick SiO2 slides (76.2 × 25.4 × 1.0 mm3; Thermo Fisher Scientific) and 5-mm-thick SiO2 slides (75.0 × 25.0 × 5.0 mm3; Präzisions Glas & Optik). The desiccator was evacuated to less than 100 mbar, closed, and the reaction was allowed to proceed for 30 min. Before measurement, the PFOTS surfaces were rinsed with ethanol to remove any unbound silanes. (2) PS films on gold, 1-mm-thick and 5-mm-thick SiO2 slides were prepared by dip coating. To get gold substrates, 30 nm gold was sputtered onto 75 × 25 mm2 glass slides that had been precoated with 5 nm chromium to improve adhesion. The solution consisted of 1 wt% PS (molecular weight, 192 kg mol–1, ε = 2.6; Sigma-Aldrich) in toluene. After moving down the substrates at a speed of 90 mm min–1 into the solution and waiting for 10 s, the substrates were moved up again at a speed of 90 mm min–1. Finally, the films were annealed in an oven at 120 °C under a vacuum for 24 h. The PS films were 20 nm thick measured by a profiler (P-7 stylus profiler, KLA-Tencor). (3) Teflon AF1600 (Teflon) films on gold, 1-mm-thick and 5-mm-thick SiO2 slides were prepared by dip coating. Sputter-coated gold glass slides (see above) or SiO2 slides were immersed into 1 wt% Teflon AF1600 (ε = 1.9; Sigma-Aldrich) in Perfluoro-2-butyltetrahydrofuran (FC-75, 97%, Fisher Scientific) at a speed of 90 mm min–1. After being immersed for 10 s, the substrates were withdrawn from the solution at a constant speed of 10 mm min–1. Finally, the films on the substrates were annealed at 160 °C in a vacuum for 24 h. Teflon AF1600 films were 60 nm thick to avoid dewetting. We determined that the roughness increased with an increase in film thickness (Supplementary Section 20). (4) PDMS polymer brushes on Si wafers, 1-mm-thick and 5-mm-thick SiO2 slides were prepared as described elsewhere51. After O2-plasma cleaning (see above), few PDMS drops (molecular weight, 6 kg mol−1; Alfa Aesar) were deposited on a Si wafer or SiO2. After the PDMS drop spread and covered the substrates, the samples were kept at 22−23 °C and 30−60% relative humidity for 24–48 h. Then, they were rinsed with toluene and sonicated in toluene, ethanol and deionized water for 10 min each to wash away any unbound PDMS. The brushes were ~3 nm thick1. (5) 1H,1H,2H,2H-perfluorodecanethiol (thiols) monolayers on gold: directly after the preparation of the gold-coated glass slide (see above), the surfaces were immersed in a 1 mM ethanolic thiol (≥96.0%; Sigma-Aldrich) solution for 24 h. Then, the surfaces were rinsed by pure ethanol and dried by Ar2 blowing.
SFM imaging
All the hydrophobic surfaces were studied using SFM (Dimension Icon, Bruker) in the tapping mode (Supplementary Fig. 2). The SFM tips with a nominal resonance frequency of 300 kHz and spring constant of 26 N m–1 were used (160AC-NA, OPUS). The root-mean-squared roughness was determined on the areas of 0.5 × 0.5 μm2 for each sample. The error was around 0.1 nm, except for the thiols-on-gold and PFOTS samples, where it was 0.2 nm. The errors were determined from variations observed at different positions on the samples and variations in the different samples.
Static contact angle measurements
‘Static’ advancing and receding contact angles, namely, \(\varTheta _\mathrm{a}^0\) and \(\varTheta _\mathrm{r}^0\), respectively, were measured with sessile water drops (OCA 35, DataPhysics Instruments). An 8 μl water drop was deposited on the surface. Then, 16 μl deionized water was pumped into the drop and subsequently sucked out at the rate of 0.5 μl s–1 by a Hamilton syringe connected to a hydrophobic needle. The process was repeated three times without interruption. During inflation and deflation, the drops were imaged in the side view. Then, \(\varTheta _\mathrm{a}^0\) and \(\varTheta _\mathrm{r}^0\) were calculated by fitting an ellipse model to the contour images.
Data availability
Source data are provided with this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
Change history
17 July 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41567-023-02173-6
References
Tuteja, A. et al. Designing superoleophobic surfaces. Science 318, 1618–1622 (2007).
Wang, L. M. & McCarthy, T. J. Covalently attached liquids: instant omniphobic surfaces with unprecedented repellency. Angew. Chem. Int. Ed. 55, 244–248 (2016).
Huhtamaki, T., Tian, X. L., Korhonen, J. T. & Ras, R. H. A. Surface-wetting characterization using contact-angle measurements. Nat. Protoc. 13, 1521–1538 (2018).
Tadmor, R. Open problems in wetting phenomena: pinning retention forces. Langmuir 37, 6357–6372 (2021).
Gao, N. et al. How drops start sliding over solid surfaces. Nat. Phys. 14, 191–196 (2017).
Backholm, M. et al. Water droplet friction and rolling dynamics on superhydrophobic surfaces. Nat. Commun. Mater. 1, 64 (2020).
Lin, Z. H., Cheng, G., Lee, S., Pradel, K. C. & Wang, Z. L. Harvesting water drop energy by a sequential contact-electrification and electrostatic-induction process. Adv. Mater. 26, 4690–4696 (2014).
Sun, Y. J., Huang, X. & Soh, S. Using the gravitational energy of water to generate power by separation of charge at interfaces. Chem. Sci. 6, 3347–3353 (2015).
Park, J. et al. Identification of droplet-flow-induced electric energy on electrolyte–insulator–semiconductor structure. J. Am. Chem. Soc. 139, 10968–10971 (2017).
Boamah, M. D. et al. Energy conversion via metal nanolayers. Proc. Natl Acad. Sci. USA 116, 16210–16215 (2019).
Helseth, L. E. A water droplet-powered sensor based on charge transfer to a flow-through front surface electrode. Nano Energy 73, 104809 (2020).
Xu, W. H. et al. A droplet-based electricity generator with high instantaneous power density. Nature 578, 392–396 (2020).
Wu, H., Mendel, N., van den Ende, D., Zhou, G. F. & Mugele, F. Energy harvesting from drops impacting onto charged surfaces. Phys. Rev. Lett. 125, 078301 (2020).
Wang, K. Q. & Li, J. J. Electricity generation from the interaction of liquid–solid interface: a review. J. Mater. Chem. A 9, 8870–8895 (2021).
Zhang, J. Y., Lin, S. Q., Zheng, M. L. & Wang, Z. L. Triboelectric nanogenerator as a probe for measuring the charge transfer between liquid and solid surfaces. ACS Nano 15, 14830–14837 (2021).
de Gennes, P. G. Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863 (1985).
Suzuki, S., Nakajima, A., Kameshima, Y. & Okada, K. Elongation and contraction of water droplet during sliding on the silicon surface treated by fluoroalkylsilane. Surf. Sci. 557, L163–L168 (2004).
Starov, V. M., Velarde, M. G. & Radke, C. J. Wetting and Spreading Dynamics (CRC Press, 2007).
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. Wetting and spreading. Rev. Mod. Phys. 81, 739–805 (2009).
Snoeijer, J. H. & Andreotti, B. Moving contact lines: scales, regimes, and dynamical transitions. Ann. Rev. Fluid Mech. 45, 269–292 (2013).
Olin, P., Lindstrom, S. B., Pettersson, T. & Wagberg, L. Water drop friction on superhydrophobic surfaces. Langmuir 29, 9079–9089 (2013).
Perrin, H., Lhermerout, R., Davitt, K., Rolley, E. & Andreotti, B. Defects at the nanoscale impact contact line motion at all scales. Phys. Rev. Lett. 116, 184502 (2016).
Marsh, J. A., Garoff, S. & Dussan, E. B. Dynamic contact angles and hydrodynamics near a moving contact line. Phys. Rev. Lett. 70, 2778–2781 (1993).
Kim, H. Y., Lee, H. J. & Kang, B. H. Sliding of liquid drops down an inclined solid surface. J. Colloid Interface Sci. 247, 372–380 (2002).
Le Grand, N., Daerr, A. & Limat, L. Shape and motion of drops sliding down an inclined plane. J. Fluid Mech. 541, 293–315 (2005).
Furmidge, C. G. L. Studies at phase interfaces. I. The sliding of liquid drops on solid surfaces and a theory for spray retention. J. Colloid Sci. 17, 309–324 (1962).
Wolfram, E. & Faust, R. in Wetting, Spreading and Adhesion (ed Padday, J. F.) 213–222 (Academic Press, 1978).
Extrand, C. W. & Kumagai, Y. Liquid drops on an inclined plane: the relation between contact angles, drop shape, and retentive force. J. Colloid Interface Sci. 170, 515–521 (1995).
Antonini, C., Carmona, F. J., Pierce, E., Marengo, M. & Amirfazli, A. General methodology for evaluating the adhesion force of drops and bubbles on solid surfaces. Langmuir 25, 6143–6154 (2009).
Semprebon, C. & Brinkmann, M. On the onset of motion of sliding drops. Soft Matter 10, 3325–3334 (2014).
Macdougall, G. & Ockrent, C. Surface energy relations in liquid/solid systems. I. The adhesion of liquids to solids and a new method of determining the surface tension of liquids. Proc. R. Soc. Lond. A 180, 151–173 (1942).
Dimitrakopoulos, P. & Higdon, J. J. L. On the gravitational displacement of three-dimensional fluid droplets from inclined solid surfaces. J. Fluid Mech. 395, 181–209 (1999).
ElSherbini, A. & Jacobi, A. Retention forces and contact angles for critical liquid drops on non-horizontal surfaces. J. Colloid Interface Sci. 299, 841–849 (2006).
Sakai, M. et al. Direct observation of internal fluidity in a water droplet during sliding on hydrophobic surfaces. Langmuir 22, 4906–4909 (2006).
Richard, D. & Quéré, D. Viscous drops rolling on a tilted non-wettable solid. Europhys. Lett. 48, 286–291 (1999).
Yilbas, B. S., Al-Sharafi, A., Ali, H. & Al-Aqeeli, N. Dynamics of a water droplet on a hydrophobic inclined surface: influence of droplet size and surface inclination angle on droplet rolling. RSC Adv. 7, 48806–48818 (2017).
Yatsuzuka, K., Mizuno, Y. & Asano, K. Electrification phenomena of pure water droplets dripping and sliding on a polymer surface. J. Electrost. 32, 157–171 (1994).
Shahzad, A., Wijewardhana, K. R. & Song, J. K. Contact electrification efficiency dependence on surface energy at the water-solid interface. Appl. Phys. Lett. 113, 023901 (2018).
Stetten, A. Z., Golovko, D. S., Weber, S. A. L. & Butt, H. J. Slide electrification: charging of surfaces by moving water drops. Soft Matter 15, 8667–8679 (2019).
Sun, Q. et al. Surface charge printing for programmed droplet transport. Nat. Mater. 18, 936–941 (2019).
Zhang, W. L., Sun, Q. Q., Butt, H. J., Wang, Z. K. & Deng, X. Surface charges as a versatile platform for emerging applications. Sci. Bull. 65, 1052–1054 (2020).
Lin, S. Q., Xu, L., Wang, A. C. & Wang, Z. L. Quantifying electron-transfer in liquid-solid contact electrification and the formation of electric double-layer. Nat. Commun. 11, 399 (2020).
Choi, D. et al. Spontaneous electrical charging of droplets by conventional pipetting. Sci. Rep. 3, 2037 (2013).
He, B. & Darhuber, A. A. Electrical surface charge patterns induced by droplets sliding over polymer and photoresist surfaces. J. Micromech. Microeng. 29, 105002 (2019).
Nauruzbayeva, J. et al. Electrification at water–hydrophobe interfaces. Nat. Commun. 11, 5285 (2020).
Poli, E., Jong, K. H. & Hassanali, A. Charge transfer as a ubiquitous mechanism in determining the negative charge at hydrophobic interfaces. Nat. Commun. 11, 901 (2020).
Yan, X. B. et al. Central role of bicarbonate anions in charging water/hydrophobic interfaces. J. Phys. Chem. Lett. 9, 96–103 (2018).
Mugele, F. & Heikenfeld, J. Electrowetting: Fundamental Principles and Practical Applications (Wiley-VCH, 2019).
Yarnold, G. D. The motion of a mercury index in a capillary tube. Proc. Phys. Soc. 50, 540–552 (1938).
Shikhmurzaev, Y. D. The moving contact line on a smooth solid surface. Int. J. Multiph. Flow 19, 589–610 (1993).
Teisala, H., Baumli, P., Weber, S. A. L., Vollmer, D. & Butt, H. J. Grafting silicone at room temperature—a transparent, scratch-resistant nonstick molecular coating. Langmuir 36, 4416–4431 (2020).
Acknowledgements
We thank Z. Wang (Hong Kong) and R. Ras (Aalto) for critically reading the manuscript and W. Scholdei for technical help. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 883631) (A.Z.S., H.B., P.B. and H.-J.B.). We further acknowledge financial support by the German Research Society via the CRC 1194 (project ID 265191195) ‘Interaction between transport and wetting processes’, projects A02 (H.M.), B07 (F.B. and H.M.) and C07 (A.S., H.-J.B. and R.B.) and the Priority Programme 2171 ‘Dynamic wetting of flexible, adaptive and switchable surfaces’ (grant no. BU 1556/36: X.L., H.-J.B. and R.B.).
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
X.L. prepared the samples, performed the tilted-plate experiments and analysed the data. X.L., A.S. and R.B. designed the tilted-plate setup. P.B., A.Z.S. and S.A.L.W. measured the drop charges. H.B. and S.A.L.W. numerically calculated the electrostatic force on a drop. F.B. and H.M. carried out the numerical diffuse-interface simulations of drop motion. S.A.L.W., S.H., M.T.S. and H.-J.B. derived the analytical theory. H.-J.B. derived the concept of extracting the electrostatic force from the equation of motion. All the authors discussed and interpreted the results and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Matthew Gebbie and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–20, Tables 1 and 2 and Figs. 1–27.
Supplementary Video 1
Video of water drops impacting Teflon-coated surfaces.
Source data
Source Data Fig. 1
Raw videos for the data in Fig. 1.
Source Data Fig. 2
Details for the plots in Fig. 2.
Source Data Fig. 3
Details for the plots in Fig. 3.
Source Data Fig. 4
Details for the plots in Fig. 4.
Source Data Fig. 5
Details for the plots in Fig. 5.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, X., Bista, P., Stetten, A.Z. et al. Spontaneous charging affects the motion of sliding drops. Nat. Phys. 18, 713–719 (2022). https://doi.org/10.1038/s41567-022-01563-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01563-6
This article is cited by
-
Droplet slipperiness despite surface heterogeneity at molecular scale
Nature Chemistry (2024)
-
Contribution of wedge and bulk viscous forces in droplets moving on inclined surfaces
Theoretical and Computational Fluid Dynamics (2024)
-
Water-solid contact electrification and catalysis adjusted by surface functional groups
Nano Research (2024)
-
Kinetic drop friction
Nature Communications (2023)
-
Tailoring vapor film beneath a Leidenfrost drop
Nature Communications (2023)