Observation of a reduced-turbulence regime with boron powder injection in a stellarator

Abstract

In state-of-the-art stellarators, turbulence is a major cause of the degradation of plasma confinement. To maximize confinement, which eventually determines the amount of nuclear fusion reactions, turbulent transport needs to be reduced. Here we report the observation of a confinement regime in a stellarator plasma that is characterized by increased confinement and reduced turbulent fluctuations. The transition to this regime is driven by the injection of submillimetric boron powder grains into the plasma. With the line-averaged electron density being kept constant, we observe a substantial increase of stored energy and electron and ion temperatures. At the same time, the amplitude of the plasma turbulent fluctuations is halved. While lower frequency fluctuations are damped, higher frequency modes in the range between 100 and 200 kHz are excited. We have observed this regime for different heating schemes, namely with both electron and ion cyclotron resonant radio frequencies and neutral beams, for both directions of the magnetic field and both hydrogen and deuterium plasmas.

Main

Stellarators are one of the most promising concepts for magnetic confined nuclear fusion, which could provide a clean alternative to fossil fuels and nuclear fission for mass energy production. Unlike tokamaks, their 3D magnetic field is provided entirely by external coils, removing the need for a current to flow into the plasma, which makes it prone to instabilities and violent disruptions. This also allows the magnetic field to be tailored to minimize neoclassical (due to collisions) transport and improve confinement¹. For present day stellarators, the biggest degradation of confinement is given by plasma turbulence. This results in an increased ‘anomalous’ transport contribution, typically an order of magnitude higher than the neoclassical transport contribution for particles² and accounting for more than 50% of the energy transport³. While in principle possible, optimizing the stellarator magnetic field to reduce turbulent transport is extremely challenging due to the huge computational cost of 3D turbulence simulations. Furthermore, generally in tokamaks, turbulent transport dominates over collisional transport³. It is therefore fundamental to reduce turbulence in order to maximise the plasma confinement, finally determining the amount of fusion reactions.

In this Article, we report the observation of a confinement regime in the Large Helical Device (LHD) stellarator⁴, characterized by widespread reduction of turbulence across the plasma cross section. In this regime, the line-averaged density remains unvaried and both ion and electron temperatures increase remarkably, without violent periodic bursts (edge localized modes) typical of the high confinement regime (H-mode, as opposed to the baseline low confinement regime, L-mode), previously observed in both tokamaks and stellarators⁵. The transition to this regime, observed at constant heating power and for different heating sources, is triggered by the injection of submillimetric boron (B) powder into the plasma.

Impurity powder injection experiments

The impurity powder dropper (IPD) is a device for injecting controlled amounts of submillimetre powder grains into the plasma under the action of gravity⁶. Its main application is to perform a real-time boronization by injecting B powder (and B composites like BN and B₄C) into the plasma. The powder, penetrating into the hot plasma, evaporates and the resulting B ions are eventually deposited on the plasma-facing surfaces creating a thin boron layer. Advantages over the standard glow discharge boronization include no need for the toxic diborane gas B₂H₆ or to interrupt the plasma operation. This technique has already been shown to improve wall conditioning in tokamaks^7,8,9,10. It reduces wall recycling and impurity content, which allows the plasma performances to be improved by accessing lower plasma collisionalities, similarly to the case of glow discharge boronization. Furthermore, as these experiments have been mainly performed in H-mode plasmas, the IPD has revealed itself an effective tool for suppression of edge-localized modes, allowing access to an H-mode free of these violent bursts¹¹. Nevertheless, a widespread turbulence reduction and temperature increase like the one reported in this Article has not been previously observed in the powder injection experiments performed on tokamaks, or following a glow discharge boronization. Conversely, in the EAST tokamak, edge turbulence is observed to be enhanced during suppression of edge-localized modes with B powder injection¹². Recently, pulsed injection of B₄C powder has been employed on the W7-X stellarator, showing a transient improvement of confinement¹³ with an increase in ion temperature while the variation with respect to the baseline level of electron temperature and stored energy assumes both positive and negative values between consecutive powder injection pulses. The improvement in performance is most likely to be a result of the modification of the plasma profiles and a reversal of the radial electric field in the plasma core, switching from the electron-root regime to the better confining ion-root regime.

The IPD has recently been installed on the LHD, with the final goals of improving the plasma performances and assessing the viability of the real-time boronization technique in steady-state operation. Indeed, the LHD is capable of extremely long discharges of up to one hour. The installation of the IPD on the LHD has been guided by predictive simulations with the coupled EMC3-EIRENE and DUSTT codes¹⁴, maximising the penetration of the powder into the plasma. The successful injection of B and BN powder in the unique LHD plasma configuration, featuring a double-null-like cross section with a predominantly poloidal magnetic field in the divertor coupled to the confined plasma by a thick ergodic layer, has been demonstrated in four-second-long plasmas¹⁵ for a wide range of mass injection rates, plasma density and heating power.

Performance improvement and turbulence suppression

A new set of powder injection experiments has been performed on the LHD, featuring longer plasma duration, in the ‘inward shifted’ magnetic configuration (position of the magnetic axis R_ax = 3.6 m). B powder grains with diameter d = 150 μm have been injected for a duration of t_d ≥ 5 s in plasmas with different heating sources. A few seconds into powder injection, the plasma performance is observed to improve, with marked increase of both electron and ion temperature (T_e, T_i) and plasma stored energy W_p. Four different examples are shown in Fig. 1, corresponding to different heating schemes: both electron and ion cyclotron resonant heating for Fig. 1a, electron cyclotron resonant heating only in Fig. 1b (but with a perpendicular pulsed diagnostic neutral beam for charge-exchange spectroscopy), ~3.5 MW of neutral beams in Fig. 1c and ~6 MW of neutral beams in Fig. 1d. The magnetic field direction for the case in Fig. 1d is reversed with respect to the cases in Fig. 1a–c. The main plasma ion is deuterium (D) in Fig. 1a,b, while it is hydrogen (H) in Fig. 1c,d. For all cases, the line-averaged density is in the range 2.7 ≤ n_e,av (10¹⁹ m⁻³) ≤ 3.7. The relative increases of T_e, T_i and W_p between before and during B powder injection are, on average, 〈ΔT_e/T_e〉 = 27%, 〈ΔT_i/T_i〉 = 25% and 〈ΔW_p/W_p〉 = 17%, but ΔT_i/T_i can be as high as 37% with respect to the reference discharge in the case in Fig. 1d.

Fig. 1: Time traces of discharges with improved performances during boron powder injection.

a–d, From top to bottom: line-averaged density n_e,av; input power P_in separated by different sources: ion and electron cyclotron resonant heating (ICH, ECH), tangential neutral beam (NB) and perpendicular diagnostic beam (pNB); electron (solid) and ion (dotted) temperature T_e and T_i; stored energy W_p; injected boron mass rate (dotted, left axis) and BV spectroscopic line (solid, right axis). Red colour for shots with B powder injection, blue for reference shots (no powder). Main plasma ion is D for a and b and H for c and d. The magnetic field direction for d is reversed with respect to a–c.

For all cases, a discharge with B powder injection (red) is compared with a reference discharge without powder (blue). We note that in Fig. 1b–d the pulsed operation of the diagnostic beam results in periodic variations of most considered quantities. In Fig. 1c, large variations in the plasma at t ≈ 5.3 s and t ≈ 7.2 s are due to the change of neutral beams, varying from counter-current to co-current direction and vice versa.

The effect of B powder on the plasma can be better appreciated in Fig. 1a, where the gas puff is provided in feed-forward mode. The powder is dropped at t ≈ 22 s and after approximately 1 s of free fall it enters the plasma, where it is heated and evaporates. The effective injection and vaporization of the powder is confirmed by the sharp increase in the BV line measured by ultraviolet spectroscopy¹⁶. Due to the extra electron source, the line-averaged electron density n_e,av starts to increase. However, after a few seconds, n_e,av decreases below the reference level: this is an effect of the real-time wall conditioning provided by the deposited boron, effectively reducing the recycling at the wall. In the other cases (Fig. 1b–d) the gas puff is operated with a feedback to keep the line-averaged density constant and this effect is masked.

Even though n_e,av remains unvaried, the powder injection changes the shape of the electron density n_e profile, as shown for one of the previously discussed shots in Fig. 2. During powder injection, n_e is increased in the edge region 0.7 < r_eff/a₉₉ < 1, while n_e is slightly decreased for r_eff/a₉₉ < 0.7, rendering the profile more hollow. Here, r_eff is the effective minor radius and a₉₉ is the minor radius of the flux surface enclosing 99% of the stored energy. Correspondingly, the slope of the electron temperature profile T_e is more strongly increased in the edge region. A similar change is also observed for the profiles of ion temperature T_i. The increase of n_e in the edge region is consistent with the powder being vaporized around the last closed flux surface (corresponding to r_eff/a₉₉ ≈ 1), as it results from coupled EMC3-EIRENE (ref. ¹⁷) and DUSTT (ref. ¹⁸) simulations (Fig. 2d). Indeed the powder particles, initially dropped vertically, are deflected by the plasma flow in the divertor leg; nevertheless, they reach the main plasma where they are completely evaporated, depositing neutral B atoms in the range 1 ≤ r_eff/a₉₉ ≤ 1.06, as shown in Fig. 2e, where the B neutral source is remapped on the normalized radial coordinate r_eff/a₉₉ for all discussed cases. Consequently, the ion effective charge is estimated to increase on average from 1.3 to 1.6 after boron injection and the confinement time of B ions in the plasma is estimated to be ~1 s (Methods). In addition to the extra electron source provided by the powder, the created B ions are deposited on the plasma-facing surfaces, reducing hydrogen recycling and impurity influx. This results in a twofold reduction of n_e in the divertor, as measured by embedded Langmuir probe arrays. The time evolution of the peak value of n_e at the strike point is plotted in black in Fig. 3c for a shot with powder injection (solid line) and for the reference discharge (dotted line). Hα radiation is also decreased (red traces), suggesting a reduction of recycling. Another indication of the effective real-time boronization is the reduction of impurity influx from the plasma-facing components (Fig. 3d), as suggested from the decrease in CVI (red) and FeXVI (blue) radiation lines. The decrease in C concentration is also confirmed by charge-exchange measurements. The combination of the two aforementioned mechanisms, namely the increase of n_e close to the last closed flux surface due to the powder injection and the decrease of n_e at the divertor, causes the density profile to steepen in the plasma edge, as shown in Fig. 3a, where the difference in normalized gradient (dn_e/dρ)/n_e between the powder injection shot and the no-powder reference is plotted, with ρ = r_eff/a₉₉. The steepening of the gradient appears to originate around r_eff/a₉₉ ≥ 1 and propagate inwards, together with an increase of the electron temperature gradient (Fig. 3b).

Fig. 2: Plasma spatial profiles and boron source.

a–c, Measured radial profiles of electron density n_e (a), electron temperature T_e (b) and ion temperature T_i (c) averaged over a 100 ms time window, in the case with (red) and without (blue) B powder injection. Error bars represent standard deviation in time. Polynomial fits of the profiles are shown with solid lines (Methods). d, T_e from EMC3-EIRENE simulations for case #167,234, together with B powder grain trajectory (solid line) computed by the DUSTT code, with the resulting B neutral atom source (dots). R and Z are the radial and vertical coordinates in a cylindrical frame of reference with its origin on the torus axis. e, B neutral source remapped on the normalized radial coordinate r_eff/a₉₉, for all discussed cases.

Fig. 3: Real-time wall conditioning and profile modification.

a,b, Time evolution of difference of normalized gradient between a powder injection shot (#166,256) and its reference (#166,254) for electron density (a) and temperature (b). c, Peak value of divertor density measured by Langmuir probes (black, left axis) and Hα radiation (red, right axis). d, Evolution of intensity of UV radiation normalized to the electron density I_UV/n_e for spectroscopic lines CVI (red), FeXVI (blue) and BV (black). e, Average value of the density fluctuation amplitude measured by phase-contrast imaging 〈δn〉_ρ. Solid lines are for the powder injection shot #166,256 and dotted lines are for the reference #166,254. Periodic oscillations at 3.33 Hz are due to the pulsed operation of the diagnostic neutral beam.

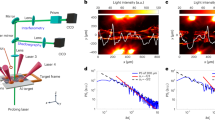
Simultaneously, the turbulent fluctuation level in the confined plasma is observed to be reduced to approximately half its value before powder injection as shown in Fig. 3e. This figure shows the amplitude of the density fluctuations measured by 2D phase-contrast imaging^19,20 averaged over the whole plasma cross section.

Radially resolved profiles of the density fluctuation amplitude and the velocity in the direction perpendicular to the field line v_⊥ (directed along the poloidal direction of the flux surface) are plotted in Fig. 4a,b before (dashed lines) and during (solid lines) B powder injection. A discharge with B powder injection (red) is compared with a reference shot (blue). As the turbulent fluctuation amplitude is substantially reduced across the whole cross section (no measurements are available for ∣r_eff/a₉₉∣ < 0.4), the velocity v_⊥ is doubled in the edge of the plasma. v_⊥ is directed in the e-diamagnetic direction, consistent with the E × B velocity resulting from a negative radial electric field E_r < 0 and results in positive/negative values in the laboratory frame when measured at the bottom/top of the plasma r_eff/a₉₉ ≶ 0. Radially resolved power spectral densities in terms of perpendicular wave number k_⊥ are shown in Fig. 4c,d before and during B powder injection, respectively. Before the powder injection, the power spectral density peaks for wave numbers in the range 0.2 ≤ k_⊥ (mm⁻¹) ≤ 0.4, consistent with ion-temperature gradient-driven instabilities. In refs. ^21,22, similar phase-contrast imaging measurements were compared with gyrokinetic simulations, determining that the observed fluctuations are indeed due to ion temperature-gradient turbulence. Dedicated gyrokinetic simulations are needed to confirm this result for the cases discussed here and are planned for future work. During B powder injection, these ion temperature gradient-like fluctuations are substantially suppressed in the confined plasma r_eff/a₉₉ < 1 and in general across the whole spectrum. Conversely, turbulence is slightly enhanced around the last closed flux surface r_eff/a₉₉ ≈ 1, as can be seen in Fig. 4e, which shows the logarithm of the ratio of the power spectral density (PSD) during (t = t₂ = 8.5 ± 0.2 s) and before (t = t₁ = 5.2 ± 0.2 s) B powder injection

$$C={{{\mathrm{log}}}\,}_{10}\frac{\mathrm {PSD}(t={t}_{2})}{\mathrm {PSD}(t={t}_{1})}$$

(1)

so that C < 0 and C > 0 mean reduction and increase of turbulence, respectively. Turbulence is therefore reduced on most of the plasma cross section, practically suppressed in correspondence of the peaks before injection (k_⊥ ≈ 0.3 mm⁻¹) and slightly enhanced around the last closed flux surface. The additional enhancement for k_⊥ ≤ 0.1 mm⁻¹ close to the plasma core r_eff/a₉₉ ≤ 0.5 could be an artifact due to insufficient diagnostic resolution for small k values.

Fig. 4: Suppression of turbulent fluctuations.

a,b, Radial profiles of turbulent fluctuation amplitude δn (a) and the perpendicular velocity v_⊥ (b) for a powder injection shot (#166,256, red) and its reference (#166,254, blue), at t = 5.2 s (before injection, dashed lines) and t = 8.5 s (during injection, solid lines). The radial profiles are averaged over a time window of 0.4 s to avoid instantaneous variations caused by the pulsed diagnostic neutral beam. The shaded area accounts for the standard deviation in time. In b, neoclassical estimates of E × B velocity for #166,256 before (black) and during (magenta) powder injection are shown with dotted lines. c–e, Radially resolved PSD in terms of wave number for #166,256 before (c) and during (d) powder injection and their ratio (e) C as defined in equation (1).

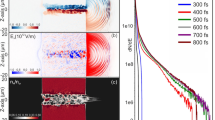
This change is reflected in the spectrogram of the line-integrated phase-contrast imaging signal (probing all r_eff/a₉₉ > 0.4), shown in Fig. 5a,b for shots #166,256 (D, heated by electron cyclotron resonant heating and pulsed diagnostic neutral beam) and #167,234 (H, neutral beam-heated). As powder is injected (white dashed line), the dominant low-frequency fluctuations (~20 and ~50 kHz for #166,256 and #167,234 respectively) are suppressed and a new mode emerges in the range 100 ≤ f (kHz) ≤ 300 (peaking at ~150 and ~200 kHz for #166,256 and #167,234 respectively). Time-averaged spectra are plotted in Fig. 5c,d for the same shots as in a and b (red) and compared to their reference shot (blue), at times before (dashed lines) and during (solid lines) powder injection. Once again, fluctuations in the range 10 ≤ f (kHz) ≤ 100 are damped, while a new peak emerges in the spectrum for f ≈ 100–200 kHz. In ref. ²³, a similar difference in phase-contrast imaging spectra has been observed between isotope mixing and non-mixing discharges. In the first case, the spectrum peaks at ~20 kHz, identified with ion temperature gradient turbulence. At lower collisionalities, ion temperature gradient turbulence is stabilized and trapped electron modes are destabilized instead at the plasma edge, where gradients are steeper, resulting in a peak at ~80 kHz in the phase-contrast imaging spectrum.

Fig. 5: Emergence of higher-frequency modes.

a,b, Spectrogram (log₁₀ (PSD)) of the line-integrated phase-contrast imaging signal for #166,256 (a) and #167,234 (b). The white dashed lines indicates the approximate time of the boron powder entering the plasma. c,d, Comparison of turbulence PSD for the B injection shot (red) and the reference shot (blue), at time before (dashed lines) and during (solid lines) powder injection, time averaged over a window of 0.4 s, in order to attenuate the variations due to the pulsed diagnostic neutral beam. The shaded areas represent the standard deviation in time.

The decrease in turbulence is observed on the whole cross section, except close to the last closed flux surface region r_eff/a₉₉ ≈ 1. This is different from the case of an H-mode, where turbulence is suppressed in the vicinity of the last closed flux surface only, due to an increased shear in poloidal velocity and therefore in the radial electric field E_r, since the poloidal velocity is mainly given by the E × B drift. In ref. ¹³, transient confinement improvement has been observed in W7-X during pulsed B₄C powder injection, which has been judged to be consistent with the reversal of E_r, transitioning from the electron-root regime (outwards directed E_r > 0) to a better confining ion-root regime (inwards directed E_r < 0), with E_r becoming transiently more negative (up to twofold) during the powder injection bursts. In our case, in general the discharges are already in the ion-root regime before powder injection and remain so during the B injection, where no significant change in radial electric field strength is expected. Indeed, the ambipolar radial electric field has been computed using the neoclassical transport code SFINCS (ref. ²⁴), for all cases (except #164,645 where no T_i measurement is available), comparing plasma with and without powder injection. In all cases, no change in E_r that could result in an improvement of confinement emerges from the simulation results (Extended Data Fig. 1). The resulting (neoclassical) E × B velocity is plotted in Fig. 4b for #166,256 with dotted lines and shows no substantial variation between before (black) and during (magenta) powder injection, except an ~30% increase at the very edge of the plasma r_eff/a₉₉ > 0.85. This alone cannot explain the observed doubling of v_⊥, that can be partly due to the increase of up to 50% of the diamagnetic velocity v_d ∝ − ∇P × B as the pressure profile steepens, which can add up to E × B to determine the total plasma flow velocity, or to a change in phase velocity of the turbulence as higher frequency modes are excited (Fig. 5).

The increase in T_e, T_i and W_p observed during powder injection is associated with a reduced energy transport in the edge of the plasma and an increase in energy confinement time. The heat conductivities for ions and electrons, χ_i and χ_e, respectively, are computed using the DYTRANS module of TASK3D-a (ref. ²⁵) by performing a dynamics transport analysis. As a result (shown in Fig. 6 for a neutral beam heated case), both χ_i and χ_e are reduced in the plasma edge during powder injection. χ_i is reduced by up to 40% for r_eff/a₉₉ > 0.4, while χ_e is reduced by up to 50% for r_eff/a₉₉ > 0.5. The DYTRANS results are consistent with the reduction of turbulent transport in the edge of the plasma during B powder injection. As turbulent transport is reduced, the steepening of the profiles increases neoclassical transport, which allows the plasma to be maintained in a quasi steady state. SFINCS simulations confirm the increase of both heat and particle neoclassical fluxes during powder injection for r_eff/a₉₉ > 0.5.

Fig. 6: Energy transport reduction and confinement improvement.

a,b, Radial profiles of heat conductivities for ions χ_i (a) and electrons χ_e (b) as a function of the normalized effective minor radius r_eff/a₉₉, comparing a discharge with powder injection (red) with a reference discharge (blue). Shaded areas represent an estimated average relative error of 20% on the DYTRANS analysis results, obtained by comparing different time frames of the simulation. c, Measured energy confinement time τ_E during B powder injection (red squares) and for the reference shots at the same time (blue diamonds). The experimental τ_E is plotted against the predicted energy confinement time from the international stellarator scaling T_E,ISS04 (ref. ²⁶). Error bars represent standard deviation in time over a window of 200 ms.

The measured energy confinement time τ_E (red squares in Fig. 6, plotted against the value predicted from the international stellarator scaling τ_E,ISS04 (ref. ²⁶), which also describes satisfactorily the scaling of tokamak H-mode τ_E (ref. ²⁷)), is also increased during B powder injection, the improvement being between 17 and 25% when compared to the reference shot at the same time (blue diamonds).

Outlook

A confinement regime has been observed in the LHD, characterized by a substantial reduction of turbulence across the whole plasma cross section, which results in a remarkable increase in plasma performances (temperature, stored energy, confinement time). This substantially differs from the usual H-mode observed in both tokamaks and stellarators, where turbulence is suppressed only in a narrow layer close to the edge of the plasma. This locally steepens the density and temperature profiles, forming a ‘pedestal’ and resulting in violent periodic relaxations of the pedestal (edge localized modes), which are absent in our observations. While the measured relative increase in ion temperature is on average 25%, it appears to increase with the input power (cases in Fig. 1b–d), ranging from 19% for discharge #166,256, to reach a transient peak of 37% with respect to the reference discharge at the highest power for discharge #169,620. This favourable trend with the input power, even if based on the limited database of this first set of experiments, suggests thats further increasing the heating power could result in an even stronger increase in ion temperature. This is promising for reactor-relevant conditions, but needs to be confirmed by further dedicated experiments, which are planned for the LHD.

While the reason for the observed improvement of confinement is not yet clear, we suspect it to be due to the suppression of ion temperature gradient turbulence. This might be an effect of changes in the plasma profiles, in particular of the peaking of n_e in the edge, by the combined effect of the extra electron source provided by the injected powder and the real-time reduction of recycling, finally resulting in a more hollow profile in the centre of the plasma. Hollow density profiles have been reported to increase the stability of ion temperature gradient modes in the LHD, reducing turbulence fluctuations^22,28. Another possibility is turbulence being reduced by the increased effective charge Z_eff due to B injection, also referred to as plasma dilution. Indeed, increased Z_eff has also been reported to have a stabilizing effect on ion temperature gradient turbulence^29,30,31. It is more likely that the combination of the two above mentioned effects might occur in our case. Dedicated gyrokinetic simulations will be necessary to verify these hypotheses and are planned for future work. The synergistic effect of impurity content and a hollow density profile has been shown to reduce turbulence in tokamak geometry as well³². In tokamaks, where the density profile is usually peaked, hollow profiles can be achieved with pellet fueling. In this case, when combined with impurity powder injection, this regime might be accessible not only in stellarators, but also in tokamaks where so far it has not been observed. This calls for dedicated comparative cross-device experiments and/or gyrokinetic modelling, comparing different stellarator configurations as well as tokamaks, to assess whether this regime is accessible in magnetic configurations different from the one employed in the experiments discussed in this Article.

The observed turbulence reduction and temperature increase occurs on the timescale of seconds, which suggests that the real-time change in wall conditions plays a driving role. On the other hand, the concentration of B ions in the main plasma evolves on the same time scale (BV line in Fig. 3d), being determined by non-trivial impurity transport. To disentangle the role of profile modification given by the reduction in recycling from the role of an increased Z_eff on turbulence suppression, additional experiments are planned on the LHD comparing B and C powder injection.

Finally, dedicated experiments and simulations are foreseen to investigate any possible role of fast ions generated by the heating sources (neutral beams, ion cyclotron resonant heating) and their interaction with impurity ions on turbulence suppression, similar to that which was observed in ref. ³³.

Methods

Evaluation of plasma quantities and profiles

Throughout this work, the line-averaged electron density n_e,av is measured by means of far infrared interferometry (FIR). Radially resolved profiles of electron density and temperature, n_e andT_e, are measured by Thomson scattering (TS). Radially resolved profiles of ion temperature T_i are measured by charge-exchange spectroscopy (CXS). For discharges #164,644 and #164,645 in Fig. 1a, the diagnostic neutral beam was not operated and no T_i measurement from CXS is available. Using pre-calculated magnetic reconstruction from the VMEC code and a ‘best-fit’ procedure based on T_e measurements²⁵, all profiles are remapped onto the normalized coordinate ρ = r_eff/a₉₉, with r_eff the effective minor radius and a₉₉ the minor radius of the flux surface enclosing 99% of the stored energy. For each time step, the n_e, T_e and T_i spatially smoothed profiles are fitted with polynomials including only even power terms, ensuring zero derivative at r_eff/a₉₉ = 0. This provides smooth spatial profiles and gradients. The values of temperatures on the axes (Fig. 1) correspond to the fitted profiles evaluated at r_eff/a₉₉ = 0. Gradients are computed by derivation of the fitted polynomials. The relative error on the gradients can be estimated by comparing the value resulting from the derivation of the fit function with the value obtained by computing the gradient of the curves enclosing the fitted data within 95% confidence levels. The relative error on the temperature gradients is then estimated to be, on average, of the order of 1%, while the relative error on the density gradients is estimated to be ≲10%. The higher relative error on the determination of the density gradients has to be attributed to the fact that density profiles are flatter and hollow, with gradient values close to zero for part of the profile.

Evaluation of increase in performances

The relative increases in T_e, T_i and W_p noted in the text are determined from the traces of the same quantities in Fig. 1, between times t = t₁ and t = t₂ corresponding to just before and during B powder injection, respectively. The values for t_1,2 differ for the four different cases discussed, to account for the different time evolution of the different discharges and are t₁ (s) = 22.8, 6.0, 4.0, 4.0 and t₂ (s) = 27.4, 8.5, 5.2, 7.1 for the cases in Fig. 1a–d.

Powder injection and evaluation of mass rate

The IPD features four independent feeders, composed of a powder reservoir and a vibrating tray. The latter is vibrated by piezoelectric blades through a driving voltage, allowing the amplitude of the vibrations and finally the amount of powder delivered to the plasma to be controlled. Each independent feeder includes an accelerometer, measuring the vibration of the tray actuated by piezoelectric blades, finally determining the injection rate of the powder into the plasma. Calibration curves have been acquired in the laboratory, allowing the amplitude of the accelerometer signal to be converted into injected-mass rates.

Estimation of effective charge and boron ions confinement time

For the experiments discussed here, no measurement of the plasma effective charge Z_eff was available in the LHD. We estimated Z_eff by matching the plasma stored energy measured by the magnetic probes W_p with the one computed by integrating the plasma pressure profiles on the plasma volume W_p = 3/2∫_VdVn_e(T_e + T_i/Z_eff), where n_e, T_e and T_i profiles are measured by TS and CXS respectively and fitted with the procedure explained above. The method has been tested against the Z_eff that can be derived by CXS measurement of the carbon density n_C, in a case without boron powder injection, where we can assume that the main impurity in the plasma is fully ionized C (because of the LHD graphite plasma-facing components). The Z_eff computed with the two methods for #169,619 (Fig. 1d) are found to be in good agreement with Z_eff ≈ 1.3 through the whole discharge.

The confinement time of B ions in the plasma τ_B is estimated by fitting the time evolution of the BV spectroscopic line with an exponential decay. Discharge #164,645 (Fig. 1a) is used for t ≥ 29 s, allowing a few seconds after the IPD piezoelectric blades stop vibrating, to exclude the tail of particles still falling into the plasma after 2 s due to collisions with the guiding tube and between themselves, as observed in previous LHD powder dropper experiments¹⁵. As a result, τ_B = 1.07 ± 0.05 s.

Simulations with EMC3-EIRENE and DUSTT

Interpretative simulations are performed with the coupled EMC3-EIRENE (refs. ^17,34,35) and DUSTT (ref. ¹⁸) codes, after ref. ¹⁴. EMC3 is a fully-3D Monte Carlo code modelling the plasma transport in the edge and scrape-off layer and it is coupled to EIRENE, which describes the neutral dynamics. The diffusion and thermal conductivity coefficients are set by matching the experimental profiles of plasma density and ion and electron temperatures. Electron density and temperature are measured by TS, while the ion temperature is measured by CXS. The 3D plasma solutions from the EMC3-EIRENE simulations are then used as the background for the DUSTT simulations, computing the trajectory of a powder grain injected into the plasma. For these simulations, the powder grains are injected vertically at the actual IPD location with an initial velocity of 5 m s⁻¹ directed downwards, consistent with the free fall of the powder grains prior to entering the plasma. The powder material is B and the size of the modelled powder grain is 150 μm, matching those used in the experiments. As the powder grains enter the plasma, they are progressively heated up to the evaporating temperature, providing a localized source of neutral B atoms. We note that the results presented here are obtained in the case of the powder grain falling vertically into the plasma at the exact IPD location. In reality, due to collisions with the IPD guiding tube and between powder grains during their free fall, the powder grains reach the plasma with a distribution of velocities and directions. A statistical approach with randomized initial velocity and direction would be needed for a detailed comparison with the experiments and is planned for future work. EMC3-EIRENE includes a module for solving impurity transport and B ions distributions are computed for our simulations. However, EMC3 assumes quasi-neutrality, that is n_e = n_H, is unaffected by the impurity ions. This approximation, valid for tracing amounts of impurities, would not be appropriate for our experimental conditions. Furthermore, EMC3-EIRENE assumes steady-state conditions and the radial electric field is not included in the calculations, which cover only the very edge of the plasma. Therefore, an exhaustive study of the transport of B ions is not available with these tools at this time, for which global gyrokinetic simulations coupling core and scrape-off layer plasma on transport time scales would be needed.

Measurement of turbulent fluctuations

In this work, the characteristics of turbulent fluctuations are measured by means of two-dimensional phase-contrast imaging. The diagnostic system and the spectral analysis technique are detailed in refs. ^19,20. The amplitude of the density fluctuation is computed from the power spectrum integrated over ω and k as $\sqrt{{\tilde{n}}^{2}}$. The cutoff wave number of the phase-contrast imaging system has been investigated in detail in ref. ³⁶, showing how fluctuations with wave number in the range 0.1 ≤ k (mm⁻¹) ≤ 0.8 are measured, with attenuated contributions to the final spectrum for k < 0.2 mm⁻¹. The velocity of the fluctuations is computed by converting the local power spectrum from frequencies to velocities using v = ω/k and taking the first moment of the converted spectrum with respect to v (ref. ¹⁹). The resulting fluctuation phase velocity, measured in the laboratory frame, is perpendicular to the laser beam and its direction can be identified with the poloidal one.

Neoclassical calculations

The code SFINCS (Stellarator Fokker–Planck Iterative Neoclassical Conservative Solver)²⁴ is used to compute the ambipolar radial electric field E_r and the neoclassical particle and heat fluxes. Experimental profiles of n_e, T_e and T_i are used for the simulations. The value of Z_eff is estimated from the experimental data with the procedure explained above. The main impurity is assumed to be C⁶⁺ in the cases without powder injection and B⁵⁺ during powder injection. While the resulting ambipolar E_r remains mainly unvaried, the neoclassical fluxes calculated by SFINCS are sensitive to uncertainties in the plasma gradients and the impurity content (Z_eff and its profile). Therefore, the observed trends are consistent with the experimental observations, but their absolute values do not directly compare to the experimental ones. Our numerical calculations are radially local and neglect the impact of the flux-surface variation of the electrostatic potential³⁷ as well as tangential magnetic drifts.

Energy confinement time

The confinement time is computed from the time trace of the plasma stored energy W_p, smoothed in time to average over the variations provided by the perpendicular pulsed diagnostic neutral beam. For electron cyclotron resonant heating, all port-through power is assumed to be absorbed by the plasma. For ion cyclotron resonant heating, it is assumed that 75% of the input power is absorbed. For neutral beams, the absorbed power is assumed to be P_ab = P_in [1 − exp(−σn_e,avl)], where σ = 0.43 represents the effective cross-section for ionization of the neutral beam for H plasmas and l = 1.86 m (ref. ³⁸).