Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Classical non-Abelian braiding of acoustic modes

Nature Physics volume 18, pages 179–184 (2022)Cite this article

Subjects

Abstract

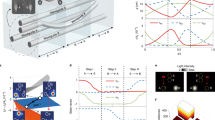
Non-Abelian braiding is regarded as an essential process for realizing quantum logic. Its realizations in quantum systems often rely on the dynamic winding of anyons, which can be challenging to obtain. Implementing braiding in a classical system could, therefore, assist the experimental study of non-Abelian physics. Here we present the realization of the non-Abelian braiding of multiple degenerate acoustic waveguide modes. The dynamics of non-Abelian braiding can be captured by the non-Abelian Berry–Wilczek–Zee phase that connects the holonomic adiabatic evolutions of multiple degenerate states. The cyclic evolution of degenerate states induces a non-Abelian geometric phase, manifesting as the exchange of states. The non-Abelian characteristics are revealed by switching the order of two distinct braiding processes involving three modes. Our work demonstrates wave manipulations based on non-Abelian braiding and logic operations.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Braiding of two states.
Fig. 2: Experimental realization of acoustic two-state braiding.
Fig. 3: Non-Abelian braiding of three degenerate states.
Fig. 4: Experimental realization of three-state non-Abelian braiding.

Similar content being viewed by others

Data availability

Source data are provided with this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

References

  1. Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).

    Article  ADS  Google Scholar 

  2. Halperin, B. I. Statistics of quasiparticles and the hierarchy of fractional quantized Hall states. Phys. Rev. Lett. 52, 1583–1586 (1984).

    Article  ADS  Google Scholar 

  3. Arovas, D., Schrieffer, J. R. & Wilczek, F. Fractional statistics and the quantum Hall effect. Phys. Rev. Lett. 53, 722–723 (1984).

    Article  ADS  Google Scholar 

  4. Stern, A. Non-Abelian states of matter. Nature 464, 187–193 (2010).

    Article  ADS  Google Scholar 

  5. Stern, A. Anyons and the quantum Hall effect—a pedagogical review. Ann. Phys. 323, 204–249 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  6. Das Sarma, S., Freedman, M. & Nayak, C. Topologically protected qubits from a possible non-Abelian fractional quantum Hall state. Phys. Rev. Lett. 94, 166802 (2005).

    Article  ADS  Google Scholar 

  7. Freedman, M., Nayak, C. & Walker, K. Towards universal topological quantum computation in the ν = 5/2 fractional quantum Hall state. Phys. Rev. B 73, 245307 (2006).

    Article  ADS  Google Scholar 

  8. Wen, X. G. Non-Abelian statistics in the fractional quantum Hall states. Phys. Rev. Lett. 66, 802–805 (1991).

    Article  ADS  MathSciNet  Google Scholar 

  9. Moore, G. & Read, N. Nonabelions in the fractional quantum hall effect. Nucl. Phys. B 360, 362–396 (1991).

    Article  ADS  MathSciNet  Google Scholar 

  10. Ivanov, D. A. Non-Abelian statistics of half-quantum vortices in p-wave superconductors. Phys. Rev. Lett. 86, 268–271 (2001).

    Article  ADS  Google Scholar 

  11. Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).

    Article  ADS  Google Scholar 

  12. Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).

    Article  ADS  Google Scholar 

  13. Sau, J. D., Lutchyn, R. M., Tewari, S. & Das Sarma, S. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 104, 040502 (2010).

    Article  ADS  Google Scholar 

  14. Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984).

    Article  ADS  MathSciNet  Google Scholar 

  15. Wilczek, F. & Zee, A. Appearance of gauge structure in simple dynamical systems. Phys. Rev. Lett. 52, 2111–2114 (1984).

    Article  ADS  MathSciNet  Google Scholar 

  16. Zanardi, P. & Rasetti, M. Holonomic quantum computation. Phys. Lett. A 264, 94–99 (1999).

    Article  ADS  MathSciNet  Google Scholar 

  17. Duan, L.-M. Geometric manipulation of trapped ions for quantum computation. Science 292, 1695–1697 (2001).

    Article  ADS  Google Scholar 

  18. Abdumalikov, A. A. Jr et al. Experimental realization of non-Abelian non-adiabatic geometric gates. Nature 496, 482–485 (2013).

    Article  ADS  Google Scholar 

  19. Simon, B. Holonomy, the quantum adiabatic theorem, and Berry’s phase. Phys. Rev. Lett. 51, 2167–2170 (1983).

    Article  ADS  MathSciNet  Google Scholar 

  20. Tomita, A. & Chiao, R. Y. Observation of Berry’s topological phase by use of an optical fiber. Phys. Rev. Lett. 57, 937–940 (1986).

    Article  ADS  Google Scholar 

  21. Shapere, A. & Wilczek, F. Geometric Phases in Physics (World Scientific, 1989).

  22. Chruscinski, D. & Jamiolkowski, A. Geometric Phases in Classical and Quantum Mechanics (Birkhäuser, 2004).

  23. Cohen, E. et al. Geometric phase from Aharonov–Bohm to Pancharatnam–Berry and beyond. Nat. Rev. Phys. 1, 437–449 (2019).

    Article  Google Scholar 

  24. Yang, Y. et al. Synthesis and observation of non-Abelian gauge fields in real space. Science 365, 1021–1025 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  25. Kremer, M., Teuber, L., Szameit, A. & Scheel, S. Optimal design strategy for non-Abelian geometric phases using Abelian gauge fields based on quantum metric. Phys. Rev. Res. 1, 033117 (2019).

    Article  Google Scholar 

  26. Chen, Y. et al. Non-Abelian gauge field optics. Nat. Commun. 10, 3125 (2019).

    Article  ADS  Google Scholar 

  27. Noh, J. et al. Braiding photonic topological zero modes. Nat. Phys. 16, 989–993 (2020).

    Article  Google Scholar 

  28. Bomzon, Z., Biener, G., Kleiner, V. & Hasman, E. Space-variant Pancharatnam–Berry phase optical elements with computer-generated subwavelength gratings. Opt. Lett. 27, 1141–1143 (2002).

    Google Scholar 

  29. Bomzon, Z., Kleiner, V. & Hasman, E. Pancharatnam–Berry phase in space-variant polarization-state manipulations with subwavelength gratings. Opt. Lett. 26, 1424–1426 (2001).

    Google Scholar 

  30. Hasman, E., Kleiner, V., Biener, G. & Niv, A. Polarization dependent focusing lens by use of quantized Pancharatnam–Berry phase diffractive optics. Appl. Phys. Lett. 82, 328–330 (2003).

    Article  ADS  Google Scholar 

  31. Li, G. et al. Continuous control of the nonlinearity phase for harmonic generations. Nat. Mater. 14, 607–612 (2015).

    Article  ADS  Google Scholar 

  32. Tymchenko, M. et al. Gradient nonlinear Pancharatnam-Berry metasurfaces. Phys. Rev. Lett. 115, 207403 (2015).

    Article  ADS  Google Scholar 

  33. Wang, S., Ma, G. & Chan, C. T. Topological transport of sound mediated by spin-redirection geometric phase. Sci. Adv. 4, eaaq1475 (2018).

    Article  ADS  Google Scholar 

  34. Iadecola, T., Schuster, T. & Chamon, C. Non-Abelian braiding of light. Phys. Rev. Lett. 117, 073901 (2016).

    Article  ADS  Google Scholar 

  35. Boross, P., Asbóth, J. K., Széchenyi, G., Oroszlány, L. & Pályi, A. Poor man’s topological quantum gate based on the Su-Schrieffer-Heeger model. Phys. Rev. B 100, 045414 (2019).

    Article  ADS  Google Scholar 

  36. Wu, Y., Liu, H., Liu, J., Jiang, H. & Xie, X. C. Double-frequency Aharonov-Bohm effect and non-Abelian braiding properties of Jackiw-Rebbi zero-mode. Natl Sci. Rev. 7, 572–578 (2020).

    Article  Google Scholar 

  37. Barlas, Y. & Prodan, E. Topological braiding of non-Abelian midgap defects in classical metamaterials. Phys. Rev. Lett. 124, 146801 (2020).

    Article  ADS  Google Scholar 

  38. Niemi, A. J. & Semenoff, G. W. Fermion number fractionization in quantum field theory. Phys. Rep. 135, 99–193 (1986).

    Article  ADS  MathSciNet  Google Scholar 

  39. Chen, Z.-G., Wang, L., Zhang, G. & Ma, G. Chiral symmetry breaking of tight-binding models in coupled acoustic-cavity systems. Phys. Rev. Appl. 14, 024023 (2020).

    Article  ADS  Google Scholar 

  40. Chen, Z.-G., Tang, W., Zhang, R.-Y., Chen, Z. & Ma, G. Landau-Zener transition in the dynamic transfer of acoustic topological states. Phys. Rev. Lett. 126, 054301 (2021).

    Article  ADS  Google Scholar 

  41. Pozar, D. M. Microwave Engineering 4th edn (Wiley, 2011).

  42. Zhang, Y.-L., Chen, Q.-D., Xia, H. & Sun, H.-B. Designable 3D nanofabrication by femtosecond laser direct writing. Nano Today 5, 435–448 (2010).

    Article  Google Scholar 

Download references

Acknowledgements

Z.-G.C. and G.M. thank W. Tang and Q. Wang for experimental assistance. This work was supported by Hong Kong Research Grants Council (12302420, 12300419, 22302718, C6013-18G, AoE/P-02/12 and 16303119), National Natural Science Foundation of China (11922416 and 11802256) and Hong Kong Baptist University (RC-SGT2/18-19/SCI/006). R.-Y.Z. and C.T.C. also acknowledge support from the Croucher Foundation (CAS20SC01).

Author information

Authors and Affiliations

  1. Department of Physics, Hong Kong Baptist University, Kowloon Tong, China

    Ze-Guo Chen & Guancong Ma

  2. Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, China

    Ruo-Yang Zhang & C. T. Chan

Authors
  1. Ze-Guo Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ruo-Yang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. C. T. Chan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Guancong Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Z.-G.C. and R.-Y.Z. developed the theory. Z.-G.C. performed the numerical simulations. Z.-G.C. and G.M. carried out the experiments with support from C.T.C. All the authors analysed the results. Z.-G.C. and G.M. wrote the manuscript with inputs from R.-Y.Z. and C.T.C. The project was initiated and supervised by G.M.

Corresponding author

Correspondence to Guancong Ma.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–12.

Source data

Source Data Fig. 2

Statistical source data.

Source Data Fig. 4

Statistical source data.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, ZG., Zhang, RY., Chan, C.T. et al. Classical non-Abelian braiding of acoustic modes. Nat. Phys. 18, 179–184 (2022). https://doi.org/10.1038/s41567-021-01431-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-021-01431-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing