Abstract
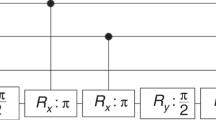
As increasingly sophisticated prototypes of quantum computers are being developed, a pressing challenge is to find computational problems that can be solved by an intermediate-scale quantum computer, but are beyond the capabilities of existing classical computers. Previous work in this direction has introduced computational problems that can be solved with certainty by quantum circuits of depth independent of the input size (so-called ‘shallow’ circuits) but cannot be solved with high probability by any shallow classical circuit. Here we show that such a separation in computational power persists even when the shallow quantum circuits are restricted to geometrically local gates in three dimensions and corrupted by noise. We also present a streamlined quantum algorithm that is shown to achieve a quantum advantage in a one-dimensional geometry. The latter may be amenable to experimental implementation with the current generation of quantum computers.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
Data availability
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
References
Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41, 303–332 (1999).
Aaronson, S. & Arkhipov, A. The computational complexity of linear optics. In Proc. 43rd Annual ACM Symposium on Theory of Computing (STOC ’11) 333–342 (Association for Computing Machinery, 2011).
Bremner, M. J., Montanaro, A. & Shepherd, D. J. Achieving quantum supremacy with sparse and noisy commuting quantum computations. Quantum 1, 8 (2017).
Farhi, E. & Harrow, A. W. Quantum supremacy through the quantum approximate optimization algorithm. Preprint at http://arXiv.org/abs/1602.07674 (2016).
Bremner, M. J., Montanaro, A. & Shepherd, D. J. Average-case complexity versus approximate simulation of commuting quantum computations. Phys. Rev. Lett. 117, 080501 (2016).
Bermejo-Vega, J. et al. Architectures for quantum simulation showing a quantum speedup. Phys. Rev. X 8, 021010 (2018).
Terhal, B. M. & DiVincenzo, D. P. Adaptive quantum computation, constant depth quantum circuits and Arthur-Merlin games. Quantum Inf. Comput. 4, 134–145 (2004).
Aaronson, S. Quantum computing, postselection, and probabilistic polynomial-time. Proc. R. Soc. A 461, 3473–3482 (2005).
Boixo, S. et al. Characterizing quantum supremacy in near-term devices. Nat. Phys. 14, 595–600 (2018).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Pednault, E. et al. Breaking the 49-qubit barrier in the simulation of quantum circuits. Preprint at https://arxiv.org/abs/1710.05867 (2017).
Boixo, S., Isakov, S. V., Smelyanskiy, V. N. & Neven, H. Simulation of low-depth quantum circuits as complex undirected graphical models. Preprint at https://arxiv.org/abs/1712.05384 (2017).
Li, R. et al. Quantum supremacy circuit simulation on Sunway TaihuLight. Preprint at https://arxiv.org/abs/1804.04797 (2018).
Chen, J. et al. Classical simulation of intermediate-size quantum circuits. Preprint at https://arxiv.org/abs/1805.01450 (2018).
Bravyi, S. et al. Simulation of quantum circuits by low-rank stabilizer decompositions. Quantum 3, 181 (2019).
Pednault, E. et al. Leveraging secondary storage to simulate deep 54-qubit Sycamore circuits. Preprint at https://arxiv.org/abs/1910.09534 (2019).
Bravyi, S., Gosset, D. & Koenig, R. Quantum advantage with shallow circuits. Science 362, 308–311 (2018).
Coudron, M., Stark, J. & Vidick, T. Trading locality for time: certifiable randomness from low-depth circuits. Preprint at https://arxiv.org/abs/1810.04233 (2018).
Gall, F. L. Average-case quantum advantage with shallow circuits. In Proc. 34th Computational Complexity Conference (CCC’19) (Ed. Shpilka, A.) 21:1–21:20 (Dagstuhl Publishing, 2019).
Watts, A. B., Kothari, R., Schaeffer, L. & Tal, A. Exponential separation between shallow quantum circuits and unbounded fan-in shallow classical circuits. In Proc. 51st Annual ACM SIGACT Symposium on Theory of Computing—STOC’19 515–526 (Association for Computing Machinery, 2019).
Peres, A. Incompatible results of quantum measurements. Phys. Lett. A 151, 107–108 (1990).
Mermin, N. D. Simple unified form for the major no-hidden-variables theorems. Phys. Rev. Lett. 65, 3373–3376 (1990).
Gottesman, D. Fault-tolerant quantum computation with constant overhead. Preprint at https://arxiv.org/abs/1310.2984 (2013).
Fawzi, O., Grospellier, A. & Leverrier, A. Constant overhead quantum fault-tolerance with quantum expander codes. In Proc. 59th IEEE Annual Symposium on Foundations of Computer Science (FOCS’18) 743–754 (IEEE, 2018).
Bravyi, S. & Kitaev, A. Quantum codes on a lattice with boundary. Preprint at https://arxiv.org/abs/quant-ph/9811052 (1998).
Dennis, E., Kitaev, A., Landahl, A. & Preskill, J. Topological quantum memory. J. Math. Phys. 43, 4452–4505 (2002).
Fowler, A. G., Stephens, A. M. & Groszkowski, P. High-threshold universal quantum computation on the surface code. Phys. Rev. A 80, 052312 (2009).
Bombín, H. Single-shot fault-tolerant quantum error correction. Phys. Rev. X 5, 031043 (2015).
Raussendorf, R., Bravyi, S. & Harrington, J. Long-range quantum entanglement in noisy cluster states. Phys. Rev. A 71, 062313 (2005).
Moussa, J. E. Transversal Clifford gates on folded surface codes. Phys. Rev. A 94, 042316 (2016).
Calderbank, A. R. & Shor, P. W. Good quantum error-correcting codes exist. Phys. Rev. A 54, 1098–1105 (1996).
Steane, A. Multiple-particle interference and quantum error correction. Proc. R. Soc. Lond. A 452, 2551–2577 (1996).
Bravyi, S., Hastings, M. B. & Verstraete, F. Lieb-Robinson bounds and the generation of correlations and topological quantum order. Phys. Rev. Lett. 97, 050401 (2006).
Eldar, L. & Harrow, A. W. Local Hamiltonians whose ground states are hard to approximate. In Proc. 58th IEEE Annual Symposium on Foundations of Computer Science (FOCS’17) 427–438 (IEEE, 2017).
Aharonov, D. & Touati, Y. Quantum circuit depth lower bounds for homological codes. Preprint at https://arxiv.org/abs/1810.03912 (2018).
Raussendorf, R., Bravyi, S. & Harrington, J. Long-range quantum entanglement in noisy cluster states. Phys. Rev. A 71, 062313 (2005).
Aaronson, S. & Chen, L. Complexity-theoretic foundations of quantum supremacy experiments. In Proc. 32nd Computational Complexity Conference (CCC ’17) (Ed. O’Donnell, R.) 22:1–22:67 (Dagstuhl Publishing, 2017).
Bouland, A., Fefferman, B., Nirkhe, C. & Vazirani, U. Quantum supremacy and the complexity of random circuit sampling. In Proc. 10th Innovations in Theoretical Computer Science (ITCS’19) 15:1–15:2 (2019).
Movassagh, R. Cayley path and quantum computational supremacy: a proof of average-case #P-hardness of Random Circuit Sampling with quantified robustness. Preprint at https://arxiv.org/abs/1909.06210 (2019).
Aaronson, S. & Gunn, S. On the classical hardness of spoofing linear cross-entropy benchmarking. Preprint at https://arxiv.org/abs/1910.12085 (2019).
Bravyi, S. & Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A 71, 022316 (2005).
O’Gorman, J. & Campbell, E. T. Quantum computation with realistic magic-state factories. Phys. Rev. A 95, 032338 (2017).
Litinski, D. A game of surface codes: large-scale quantum computing with lattice surgery. Quantum 3, 128 (2019).
Napp, J. et al. Efficient classical simulation of random shallow 2D quantum circuits. Preprint at https://arxiv.org/abs/2001.00021 (2019).
Kahanamoku-Meyer, G. D. Forging quantum data: classically defeating an IQP-based quantum test. Preprint at https://arxiv.org/abs/1912.05547 (2019).
Acknowledgements
S.B. acknowledges support from the IBM Research Frontiers Institute and funding from the MIT-IBM Watson AI Lab under the project Machine Learning in Hilbert Space. R.K. acknowledges support by the Technical University of Munich—Institute of Advanced Study, funded by the German Excellence Initiative and the European Union Seventh Framework Programme under grant agreement no. 291763, by the DFG Cluster of Excellence 2111 (Munich Center for Quantum Science and Technology) and by the German Federal Ministry of Education through the funding programme Photonics Research Germany, contract no. 13N14776 (QCDA-QuantERA). D.G. acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC) under Discovery grant no. RGPIN-2019-04198. D.G. is a CIFAR fellow in the Quantum Information Science Program. D.G. acknowledges research funding from IBM Research. M.T. thanks the Stellenbosch Institute of Advanced Study for hosting him while part of this work was completed.
Author information
Authors and Affiliations
Contributions
All authors contributed important ideas during initial discussions and contributed equally to deriving the technical proofs and writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks Stephen Bartlett, Sergio Boixo and Bill Fefferman for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Proofs of all the results presented in the main text.
Rights and permissions
About this article
Cite this article
Bravyi, S., Gosset, D., König, R. et al. Quantum advantage with noisy shallow circuits. Nat. Phys. 16, 1040–1045 (2020). https://doi.org/10.1038/s41567-020-0948-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0948-z
This article is cited by
-
Behavior prediction of fiber optic temperature sensor based on hybrid classical quantum regression model
Quantum Machine Intelligence (2024)
-
Quantum Gaussian process regression for Bayesian optimization
Quantum Machine Intelligence (2024)
-
Scalable error mitigation for noisy quantum circuits produces competitive expectation values
Nature Physics (2023)
-
Classically verifiable quantum advantage from a computational Bell test
Nature Physics (2022)
-
Contextuality in infinite one-dimensional translation-invariant local Hamiltonians
npj Quantum Information (2022)