Abstract
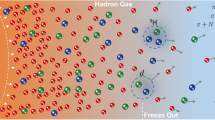
Collisions between heavy atomic nuclei at ultrarelativistic energies are carried out at particle colliders to produce the quark–gluon plasma, a state of matter where quarks and gluons are not confined into hadrons, and colour degrees of freedom are liberated. This state is thought to be produced as a transient phenomenon before it fragments into thousands of particles that reach the particle detectors. Despite two decades of investigations, one of the big open challenges1 is to obtain an experimental determination of the temperature reached in a heavy-ion collision, and a simultaneous determination of another thermodynamic quantity, such as the entropy density, that would give access to the number of degrees of freedom. Here, we obtain such a determination, utilizing state-of-the-art hydrodynamic simulations2. We define an effective temperature, averaged over the spacetime evolution of the medium. Then, using experimental data, we determine this temperature and the corresponding entropy density and speed of sound in the matter created in lead–lead collisions at the Large Hadron Collider. Our results agree with first-principles calculations from lattice quantum chromodynamics3 and confirm that a deconfined phase of matter is indeed produced.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Code availability
The hydrodynamic code used in this article is publicly available at http://www.physics.mcgill.ca/music/. The code used to generate initial conditions for hydrodynamics is publicly available at https://github.com/Duke-QCD/trento.
References
Busza, W., Rajagopal, K. & van der Schee, W. Heavy ion collisions: the big picture, and the big questions. Ann. Rev. Nucl. Part. Sci. 68, 339–376 (2018).
Romatschke P. & Romatschke U. Relativistic Fluid Dynamics In and Out of Equilibrium (Cambridge Univ. Press, 2019).
Borsanyi, S. et al. Full result for the QCD equation of state with 2 + 1 flavors. Phys. Lett. B 730, 99–104 (2014).
Schlichting, S. & Teaney, D. The first fm/c of heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 69, 447–476 (2019).
Broniowski, W. & Florkowski, W. Explanation of the RHIC p ⟂ spectra in a thermal model with expansion. Phys. Rev. Lett. 87, 272302 (2001).
Alba, P. et al. Effect of the QCD equation of state and strange hadronic resonances on multiparticle correlations in heavy ion collisions. Phys. Rev. C 98, 034909 (2018).
Mazeliauskas, A., Floerchinger, S., Grossi, E. & Teaney, D. Fast resonance decays in nuclear collisions. Eur. Phys. J. C 79, 284 (2019).
Van Hove, L. et al. Multiplicity dependence of p t spectrum as a possible signal for a phase transition in hadronic collisions. Phys. Lett. B 118, 138–140 (1982).
Campanini, R. & Ferri, G. Experimental equation of state in proton–proton and proton–antiproton collisions and phase transition to quark gluon plasma. Phys. Lett. B 703, 237–245 (2011).
McLerran, L. D., Kataja, M., Ruuskanen, P. V. & von Gersdorff, H. Studies of the hydrodynamical evolution of matter produced in fluctuations in p anti-p collisions and in ultrarelativistic nuclear collisions. 2. Transverse momentum distributions. Phys. Rev. D 34, 2755–2763 (1986).
Blaizot, J. P. & Ollitrault, J. Y. Equation of state and hydrodynamics of quark gluon plasmas. Phys. Lett. B 191, 21–26 (1987).
Ollitrault, J. Y. et al. Relativistic hydrodynamics for heavy-ion collisions. Eur. J. Phys. 29, 275–302 (2008).
Bernhard, J. E., Moreland, J. S., Bass, S. A., Liu, J. & Heinz, U. Applying Bayesian parameter estimation to relativistic heavy-ion collisions: simultaneous characterization of the initial state and quark–gluon plasma medium. Phys. Rev. C 94, 024907 (2016).
Huovinen, P. & Petreczky, P. QCD equation of state and hadron resonance gas. Nucl. Phys. A 837, 26–53 (2010).
Monnai, A. & Hirano, T. Effects of bulk viscosity at freezeout. Phys. Rev. C 80, 054906 (2009).
ALICE Collaboration Transverse momentum spectra and nuclear modification factors of charged particles in Xe–Xe collisions at \(\sqrt{{s}_{{\rm{NN}}}}\) = 5.44 TeV .Phys. Lett. B 788, 166–179 (2019).
Andronic, A., Braun-Munzinger, P., Redlich, K. & Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 561, 321–330 (2018).
Hanus, P., Mazeliauskas, A. & Reygers, K. Entropy production in pp and Pb–Pb collisions at energies available at the CERN Large Hadron Collider. Phys. Rev. C 100, 064903 (2019).
ALICE Collaboration Centrality dependence of the charged-particle multiplicity density at midrapidity in Pb–Pb collisions at \(\sqrt{{s}_{{\rm{NN}}}}\) = 5.02 TeV .Phys. Rev. Lett. 116, 222302 (2016).
ALICE Collaboration Centrality dependence of the charged-particle multiplicity density at mid-rapidity in Pb–Pb collisions at \(\sqrt{{s}_{NN}}=2.76\) TeV. Phys. Rev. Lett. 106, 032301 (2011).
ALICE Collaboration Transverse momentum spectra and nuclear modification factors of charged particles in pp, p–Pb and Pb–Pb collisions at the LHC. J. High Energy Phys. 1811, 013 (2018).
Pratt, S., Sangaline, E., Sorensen, P. & Wang, H. Constraining the equation of state of super-hadronic matter from heavy-ion collisions. Phys. Rev. Lett. 114, 202301 (2015).
PHENIX Collaboration Spectra and ratios of identified particles in Au+Au and d+Au collisions at \(\sqrt{{s}_{NN}}=200\) GeV. Phys. Rev. C 88, 024906 (2013).
Rogly, R., Giacalone, G. & Ollitrault, J. Y. Geometric scaling in symmetric nucleus–nucleus collisions. Nucl. Phys. A 982, 355–358 (2019).
Giacalone, G., Mazeliauskas, A. & Schlichting, S. Hydrodynamic attractors, initial state energy and particle production in relativistic nuclear collisions. Phys. Rev. Lett. 123, 262301 (2019).
PHOBOS Collaboration Centrality dependence of the charged particle multiplicity near mid-rapidity in Au + Au collisions at \(\sqrt{s}\) (NN) = 130-GeV and 200-GeV. Phys. Rev. C 65, 061901 (2002).
Bjorken, J. D. et al. Highly relativistic nucleus–nucleus collisions: the central rapidity region. Phys. Rev. D 27, 140–151 (1983).
Kolb P. F. & Heinz U. W. in Quark-Gluon Plasma 3 (eds Hwa, R. C. & Wang X.-N.) 634–714 (World Scientific, 2004).
Vredevoogd, J. & Pratt, S. Universal flow in the first stage of relativistic heavy ion collisions. Phys. Rev. C 79, 044915 (2009).
van der Schee, W., Romatschke, P. & Pratt, S. Fully dynamical simulation of central nuclear collisions. Phys. Rev. Lett. 111, 222302 (2013).
Keegan, L., Kurkela, A., Mazeliauskas, A. & Teaney, D. Initial conditions for hydrodynamics from weakly coupled pre-equilibrium evolution. J. High Energy Phys. 1608, 171 (2016).
Eskola, K. J., Kajantie, K. & Tuominen, K. Centrality dependence of multiplicities in ultrarelativistic nuclear collisions. Phys. Lett. B 497, 39–43 (2001).
Kolb, P. F., Heinz, U. W., Huovinen, P., Eskola, K. J. & Tuominen, K. Centrality dependence of multiplicity, transverse energy, and elliptic flow from hydrodynamics. Nucl. Phys. A 696, 197–215 (2001).
Miller, M. L., Reygers, K., Sanders, S. J. & Steinberg, P. Glauber modeling in high energy nuclear collisions. Ann. Rev. Nucl. Part. Sci. 57, 205–243 (2007).
ALICE Collaboration Centrality and pseudorapidity dependence of the charged-particle multiplicity density in Xe–Xe collisions at \(\sqrt{{s}_{{\rm{NN}}}}\) = 5.44TeV . Phys. Lett. B 790, 35–48 (2019).
ALICE Collaboration Centrality determination of Pb–Pb collisions at \(\sqrt{{s}_{NN}}\) = 2.76 TeV with ALICE. Phys. Rev. C 88, 044909 (2013).
Moreland, J. S., Bernhard, J. E. & Bass, S. A. Alternative ansatz to wounded nucleon and binary collision scaling in high-energy nuclear collisions. Phys. Rev. C 92, 011901 (2015).
Hama, Y., Kodama, T. & Socolowski, O. Jr. Topics on hydrodynamic model of nucleus–nucleus collisions. Braz. J. Phys. 35, 24–51 (2005).
Broniowski, W., Chojnacki, M. & Obara, L. Size fluctuations of the initial source and the event-by-event transverse momentum fluctuations in relativistic heavy-ion collisions. Phys. Rev. C 80, 051902 (2009).
Giacalone, G., Noronha-Hostler, J., Luzum, M. & Ollitrault, J. Y. Hydrodynamic predictions for 5.44 TeV Xe+Xe collisions. Phys. Rev. C 97, 034904 (2018).
Schenke, B., Jeon, S. & Gale, C. (3+1)D hydrodynamic simulation of relativistic heavy-ion collisions. Phys. Rev. C 82, 014903 (2010).
Schenke, B., Jeon, S. & Gale, C. Higher flow harmonics from (3+1)D event-by-event viscous hydrodynamics. Phys. Rev. C 85, 024901 (2012).
Paquet, J. F. et al. Production of photons in relativistic heavy-ion collisions. Phys. Rev. C 93, 044906 (2016).
Niemi, H., Eskola, K. J. & Paatelainen, R. Event-by-event fluctuations in a perturbative QCD + saturation + hydrodynamics model: Determining QCD matter shear viscosity in ultrarelativistic heavy-ion collisions. Phys. Rev. C 93, 024907 (2016).
Heinz, U. & Snellings, R. Collective flow and viscosity in relativistic heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 63, 123–151 (2013).
Cooper, F. & Frye, G. Comment on the single particle distribution in the hydrodynamic and statistical thermodynamic models of multiparticle production. Phys. Rev. D 10, 186–189 (1974).
Bazavov, A., HotQCD Collaboration. et al. Chiral crossover in QCD at zero and non-zero chemical potentials. Phys. Lett. B 795, 15–21 (2019).
Gale, C., Jeon, S., Schenke, B., Tribedy, P. & Venugopalan, R. Event-by-event anisotropic flow in heavy-ion collisions from combined Yang–Mills and viscous fluid dynamics. Phys. Rev. Lett. 110, 012302 (2013).
Eskola, K. J., Niemi, H., Paatelainen, R. & Tuominen, K. Predictions for multiplicities and flow harmonics in 5.44 TeV Xe+Xe collisions at the CERN Large Hadron Collider. Phys. Rev. C 97, 034911 (2018).
Weller, R. D. & Romatschke, P. One fluid to rule them all: viscous hydrodynamic description of event-by-event centralp+p, p+Pb and Pb+Pb collisions at \(\sqrt{s}=5.02\) TeV. Phys. Lett. B 774, 351–356 (2017).
Dubla, A. et al. Towards QCD-assisted hydrodynamics for heavy-ion collision phenomenology. Nucl. Phys. A 979, 251–264 (2018).
Teaney, D. et al. The effects of viscosity on spectra, elliptic flow, and HBT radii. Phys. Rev. C 68, 034913 (2003).
Dusling, K., Moore, G. D. & D., Teaney Radiative energy loss and v 2 spectra for viscous hydrodynamics. Phys. Rev. C 81, 034907 (2010).
Bozek, P. et al. Bulk and shear viscosities of matter created in relativistic heavy-ion collisions. Phys. Rev. C 81, 034909 (2010).
Teaney, D., Lauret, J. & Shuryak, E. V. Flow at the SPS and RHIC as a quark gluon plasma signature. Phys. Rev. Lett. 86, 4783–4786 (2001).
Petersen, H., Steinheimer, J., Burau, G., Bleicher, M. & Stocker, H. A fully integrated transport approach to heavy ion reactions with an intermediate hydrodynamic stage. Phys. Rev. C 78, 044901 (2008).
Petersen, H., Steinheimer, J., Bleicher, M. & Stocker, H. The <m T> excitation function: freeze-out and equation of state dependence. J. Phys. G 36, 055104 (2009).
Luo, X. Exploring the QCD phase structure with beam energy scan in heavy-ion collisions. Nucl. Phys. A 956, 75–82 (2016).
Monnai, A. & Ollitrault, J. Y. Constraining the equation of state with identified particle spectra. Phys. Rev. C 96, 044902 (2017).
Acknowledgements
F.G.G. was supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq grant 205369/2018-9 and 312932/2018-9). M.L. acknowledges support from FAPESP projects 2016/24029-6 and 2017/05685-2. F.G.G. and M.L. acknowledge support from project INCT-FNA Proc. No. 464898/2014-5 and G.G., M.L. and J.-Y.O. from USP-COFECUB (grant Uc Ph 160-16, 2015/13).
Author information
Authors and Affiliations
Contributions
F.G.G. and G.G. initiated the project and designed the figures. G.G. devised the initial conditions of the hydrodynamic calculations. F.G.G. carried out the hydrodynamic calculations. M.L. suggested the definitions of the effective temperature and effective volume. J.-Y.O. supervised the project and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks Sándor Katz and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Source Data Fig. 2
Text file containing the values plotted on the figure.
Source Data Fig. 3
Text file containing the values plotted on the figure.
Rights and permissions
About this article
Cite this article
Gardim, F.G., Giacalone, G., Luzum, M. et al. Thermodynamics of hot strong-interaction matter from ultrarelativistic nuclear collisions. Nat. Phys. 16, 615–619 (2020). https://doi.org/10.1038/s41567-020-0846-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-020-0846-4
This article is cited by
-
Strongly interacting matter exhibits deconfined behavior in massive neutron stars
Nature Communications (2023)
-
Bounding the QCD Equation of State with the Lattice
Journal of High Energy Physics (2023)
-
Effective (kinetic freeze-out) temperature, transverse flow velocity, and kinetic freeze-out volume in high energy collisions
Nuclear Science and Techniques (2020)
-
Recent development of hydrodynamic modeling in heavy-ion collisions
Nuclear Science and Techniques (2020)