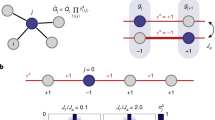
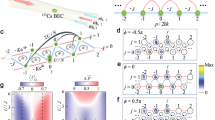
Abstract
Gauge fields that appear in models of high-energy and condensed-matter physics are dynamical quantum degrees of freedom due to their coupling to matter fields. Since the dynamics of these strongly correlated systems is hard to compute, it was proposed to implement this basic coupling mechanism in quantum simulation platforms with the ultimate goal to emulate lattice gauge theories. Here, we realize the fundamental ingredient for a density-dependent gauge field acting on ultracold fermions in an optical lattice by engineering non-trivial Peierls phases that depend on the site occupations. We propose and implement a Floquet scheme that relies on breaking time-reversal symmetry by driving the lattice simultaneously at two frequencies that are resonant with the on-site interactions. This induces density-assisted tunnelling processes that are controllable in amplitude and phase. We demonstrate techniques in a Hubbard dimer to quantify the amplitude and to directly measure the Peierls phase with respect to the single-particle hopping. The tunnel coupling features two distinct regimes as a function of the modulation amplitudes, which can be characterized by a \({\Bbb Z}_2\)-invariant. Moreover, we provide a full tomography of the winding structure of the Peierls phase around a Dirac point that appears in the driving parameter space.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data files are available from the corresponding author upon request. Source data for Figs. 2–4 and Supplementary Figs. 1d and 7 are provided in the Supplementary information.
Code availability
The source code for the fit of the Ramsey fringes is available from the corresponding author upon request.
References
Goldman, N., Juzeliunas, G., Öhberg, P. & Spielman, I. B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 77, 126401 (2014).
Cooper, N. R., Dalibard, J. & Spielman, I. B. Topological bands for ultracold atoms. Rev. Mod. Phys. 91, 015005 (2019).
Cooper, N. R. Rapidly rotating atomic gases. Adv. Phys. 57, 539–616 (2008).
Lin, Y.-J., Compton, R. L., Jiménez-García, K., Porto, J. V. & Spielman, I. B. Synthetic magnetic fields for ultracold neutral atoms. Nature 462, 628–632 (2009).
Bukov, M., D’Alessio, L. & Polkovnikov, A. Universal high-frequency behavior of periodically driven systems: from dynamical stabilization to Floquet engineering. Adv. Phys. 64, 139–226 (2015).
Eckardt, A. Colloquium: atomic quantum gases in periodically driven optical lattices. Rev. Mod. Phys. 89, 011004 (2017).
Aidelsburger, M. et al. Experimental realization of strong effective magnetic fields in an optical lattice. Phys. Rev. Lett. 107, 255301 (2011).
Miyake, H., Siviloglou, G. A., Kennedy, C. J., Burton, W. C. & Ketterle, W. Realizing the Harper Hamiltonian with laser-assisted tunneling in optical lattices. Phys. Rev. Lett. 111, 185302 (2013).
Struck, J. et al. Engineering Ising-XY spin-models in a triangular lattice using tunable artificial gauge fields. Nat. Phys. 9, 738–743 (2013).
Jotzu, G. et al. Experimental realisation of the topological Haldane model. Nature 515, 237–240 (2014).
Cheng, T.-P. & Li, L.-F. Gauge Theory of Elementary Particle Physics (Oxford Univ. Press, 1991).
Levin, M. & Wen, X. G. Colloquium: photons and electrons as emergent phenomena. Rev. Mod. Phys. 77, 871–879 (2005).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017).
Wiese, U. J. Ultracold quantum gases and lattice systems: quantum simulation of lattice gauge theories. Ann. Phys. 525, 777–796 (2013).
Zohar, E., Cirac, J. I. & Reznik, B. Quantum simulations of lattice gauge theories using ultracold atoms in optical lattices. Rep. Prog. Phys. 79, 014401 (2015).
Dalmonte, M. & Montangero, S. Lattice gauge theory simulations in the quantum information era. Contemp. Phys. 57, 388–412 (2016).
Martinez, E. A. et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature 534, 516–519 (2016).
Edmonds, M. J., Valiente, M., Juzeliunas, G., Santos, L. & Öhberg, P. Simulating an interacting gauge theory with ultracold Bose gases. Phys. Rev. Lett. 110, 085301 (2013).
Clark, L. W. et al. Observation of density-dependent gauge fields in a Bose–Einstein condensate based on micromotion control in a shaken two-dimensional lattice. Phys. Rev. Lett. 121, 030402 (2018).
Keilmann, T., Lanzmich, S., McCulloch, I. & Roncaglia, M. Statistically induced phase transitions and anyons in 1D optical lattices. Nat. Commun. 2, 361–367 (2011).
Greschner, S., Sun, G., Poletti, D. & Santos, L. Density-dependent synthetic gauge fields using periodically modulated interactions. Phys. Rev. Lett. 113, 215303 (2014).
Greschner, S. & Santos, L. Anyon hubbard model in one-dimensional optical lattices. Phys. Rev. Lett. 115, 053002 (2015).
Bermudez, A. & Porras, D. Interaction-dependent photon-assisted tunneling in optical lattices: a quantum simulator of strongly-correlated electrons and dynamical gauge fields. New J. Phys. 17, 103021 (2015).
Cardarelli, L., Greschner, S. & Santos, L. Engineering interactions and anyon statistics by multicolor lattice-depth modulations. Phys. Rev. A 94, 023615 (2016).
Sträter, C., Srivastava, S. C. L. & Eckardt, A. Floquet realization and signatures of one-dimensional anyons in an optical lattice. Phys. Rev. Lett. 117, 205303 (2016).
Barbiero, L. et al. Coupling ultracold matter to dynamical gauge fields in optical lattices: from flux-attachment to ℤ2 lattice gauge theories. Preprint at https://arxiv.org/abs/1810.02777 (2018).
Struck, J. et al. Tunable gauge potential for neutral and spinless particles in driven optical lattices. Phys. Rev. Lett. 108, 225304 (2012).
Stöferle, T., Moritz, H., Schori, C., Köhl, M. & Esslinger, T. Transition from a strongly interacting 1D superfluid to a Mott insulator. Phys. Rev. Lett. 92, 130403 (2004).
Jördens, R., Strohmaier, N., Günter, K. J., Moritz, H. & Esslinger, T. A Mott insulator of fermionic atoms in an optical lattice. Nature 455, 204–207 (2008).
Greif, D., Tarruell, L., Uehlinger, T., Jördens, R. & Esslinger, T. Probing nearest-neighbor correlations of ultracold fermions in an optical lattice. Phys. Rev. Lett. 106, 145302 (2011).
Chen, Y.-A. et al. Controlling correlated tunneling and superexchange interactions with ac-driven optical lattices. Phys. Rev. Lett. 107, 210405 (2011).
Ma, R. et al. Photon-assisted tunneling in a biased strongly correlated Bose gas. Phys. Rev. Lett. 107, 095301 (2011).
Meinert, F., Mark, M. J., Lauber, K., Daley, A. J. & Nägerl, H.-C. Floquet engineering of correlated tunneling in the Bose–Hubbard model with ultracold atoms. Phys. Rev. Lett. 116, 205301 (2016).
Desbuquois, R. et al. Controlling the Floquet state population and observing micromotion in a periodically driven two-body quantum system. Phys. Rev. A 96, 053602 (2017).
Görg, F. et al. Enhancement and sign change of magnetic correlations in a driven quantum many-body system. Nature 553, 481–485 (2018).
Messer, M. et al. Floquet dynamics in driven Fermi–Hubbard systems. Phys. Rev. Lett. 121, 233603 (2018).
Xu, W., Morong, W., Hui, H. Y., Scarola, V. W. & DeMarco, B. Correlated spin-flip tunneling in a Fermi lattice gas. Phys. Rev. A 98, 023623 (2018).
Sandholzer, K. et al. Quantum simulation meets nonequilibrium DMFT: analysis of a periodically driven, strongly correlated Fermi–Hubbard model. Preprint at https://arxiv.org/abs/1811.12826 (2018).
Schweizer, C. et al. Floquet approach to ℤ2 lattice gauge theories with ultracold atoms in optical lattices. Nat. Phys. https://doi.org/10.1038/s41567-019-0649-7 (2019).
Jotzu, G. et al. Creating state-dependent lattices for ultracold fermions by magnetic gradient modulation. Phys. Rev. Lett. 115, 073002 (2015).
Tarruell, L., Greif, D., Uehlinger, T., Jotzu, G. & Esslinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 483, 302–305 (2012).
Greif, D., Uehlinger, T., Jotzu, G., Tarruell, L. & Esslinger, T. Short-range quantum magnetism of ultracold fermions in an optical lattice. Science 340, 1307–1310 (2013).
Acknowledgements
We thank L. Barbiero, A. Bermudez, A. Eckardt, N. Goldman, F. Grusdt, Y. Murakami, M. Rizzi, L. Santos, K. Viebahn, P. Werner and O. Zilberberg for insightful discussions, and K. Viebahn and O. Zilberberg for a careful reading of the manuscript. We acknowledge SNF (projects nos. 169320 and 182650), NCCR-QSIT, QUIC (Swiss State Secretary for Education, Research and Innovation contract no. 15.0019) and ERC advanced grant TransQ (project no. 742579) for funding.
Author information
Authors and Affiliations
Contributions
The data were measured and analysed by F.G., K.S. and J.M. The theoretical framework and measurement scheme were developed by F.G. All work was supervised by T.E. All authors contributed to planning the experiment, discussions and preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary text and Figs. 1–7.
Supplementary Data 1
Source data for Fig. 2.
Supplementary Data 2
Source data for Fig. 3.
Supplementary Data 3
Source data for Fig. 4.
Supplementary Data 4
Source data for Supplementary Fig. 1d.
Supplementary Data 5
Source data for Supplementary Fig. 7.
Rights and permissions
About this article
Cite this article
Görg, F., Sandholzer, K., Minguzzi, J. et al. Realization of density-dependent Peierls phases to engineer quantized gauge fields coupled to ultracold matter. Nat. Phys. 15, 1161–1167 (2019). https://doi.org/10.1038/s41567-019-0615-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0615-4
This article is cited by
-
Dynamical localization transition in the non-Hermitian lattice gauge theory
Communications Physics (2024)
-
Quantum simulation of fundamental particles and forces
Nature Reviews Physics (2023)
-
Floquet space exploration for the dual-dressing of a qubit
Scientific Reports (2023)
-
Prethermalization in one-dimensional quantum many-body systems with confinement
Nature Communications (2022)
-
Realizing a 1D topological gauge theory in an optically dressed BEC
Nature (2022)