Abstract
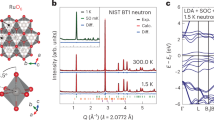
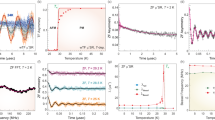
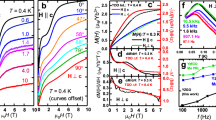
Antiferromagnetically coupled S = 1/2 spins on an isotropic triangular lattice are the paradigm of frustrated quantum magnetism, but structurally ideal realizations are rare. Here, we investigate NaYbO2, which hosts an ideal triangular lattice of effective Jeff = 1/2 moments with no inherent site disorder. No signatures of conventional magnetic order appear down to 50 mK, strongly suggesting a quantum spin liquid ground state. We observe a two-peak specific heat and a nearly quadratic temperature dependence, in agreement with expectations for a two-dimensional Dirac spin liquid. Application of a magnetic field strongly perturbs the quantum disordered ground state and induces a clear transition into a collinear ordered state, consistent with a long-predicted up–up–down structure for a triangular-lattice XXZ Hamiltonian driven by quantum fluctuations. The observation of spin liquid signatures in zero field and quantum-induced ordering in intermediate fields in the same compound demonstrates an intrinsically quantum disordered ground state. We conclude that NaYbO2 is a model, versatile platform for exploring spin liquid physics with full tunability of field and temperature.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request. Neutron data were collected on the BT-1 diffractometer and the Disk Chopper Spectrometer at the NIST Center for Neutron Research.
References
Anderson, P. W. Resonating valence bonds: a new kind of insulator? Mater. Res. Bull. 8, 153–160 (1973).
Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).
Lee, P. A. An end to the drought of quantum spin liquids. Science 321, 1306–1307 (2008).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017).
Witczak-Krempa, W., Chen, G., Kim, Y. B. & Balents, L. Correlated quantum phenomena in the strong spin–orbit regime. Annu. Rev. Condens. Matter Phys. 5, 57–82 (2014).
Zhou, Y., Kanoda, K. & Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017).
Lee, S.-S. & Lee, P. A. U(1) gauge theory of the Hubbard model: spin liquid states and possible application to κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. Lett. 95, 036403 (2005).
Itou, T., Oyamada, A., Maegawa, S., Tamura, M. & Kato, R. Quantum spin liquid in the spin-1/2 triangular antiferromagnet EtMe3Sb[Pd(dmit)2]2. Phys. Rev. B 77, 104413 (2008).
Ma, J. et al. Static and dynamical properties of the spin-1/2 equilateral triangular-lattice antiferromagnet Ba3CoSb2O9. Phys. Rev. Lett. 116, 087201 (2016).
Shirata, Y., Tanaka, H., Matsuo, A. & Kindo, K. Experimental realization of a spin-1/2 triangular-lattice Heisenberg antiferromagnet. Phys. Rev. Lett. 108, 057205 (2012).
Jackeli, G. & Ivanov, D. A. Dimer phases in quantum antiferromagnets with orbital degeneracy. Phys. Rev. B 76, 132407 (2007).
Clarke, S. J., Fowkes, A. J., Harrison, A., Ibberson, R. M. & Rosseinsky, M. J. Synthesis, structure, and magnetic properties of NaTiO2. Chem. Mater. 10, 372–384 (1998).
McQueen, T. M. et al. Successive orbital ordering transitions in NaVO2. Phys. Rev. Lett. 101, 166402 (2008).
Li, Y. et al. Gapless quantum spin liquid ground state in the two-dimensional spin-1/2 triangular antiferromagnet YbMgGaO4. Sci. Rep. 5, 16419 (2015).
Li, Y. et al. Rare-earth triangular lattice spin liquid: a single-crystal study of YbMgGaO4. Phys. Rev. Lett. 115, 167203 (2015).
Li, Y. et al. Muon spin relaxation evidence for the U(1) quantum spin-liquid ground state in the triangular antiferromagnet YbMgGaO4. Phys. Rev. Lett. 117, 097201 (2016).
Shen, Y. et al. Evidence for a spinon Fermi surface in a triangular-lattice quantum-spin-liquid candidate. Nature 540, 559–562 (2016).
Xu, Y. et al. Absence of magnetic thermal conductivity in the quantum spin-liquid candidate YbMgGaO4. Phys. Rev. Lett. 117, 267202 (2016).
Paddison, J. A. M. et al. Continuous excitations of the triangular-lattice quantum spin liquid YbMgGaO4. Nat. Phys. 13, 117–122 (2017).
Li, Y. et al. Crystalline electric-field randomness in the triangular lattice spin-liquid YbMgGaO4. Phys. Rev. Lett. 118, 107202 (2017).
Li, Y.-D., Wang, X. & Chen, G. Anisotropic spin model of strong spin–orbit-coupled triangular antiferromagnets. Phys. Rev. B 94, 035107 (2016).
Li, Y.-D., Shen, Y., Li, Y., Zhao, J. & Chen, G. Effect of spin–orbit coupling on the effective-spin correlation in YbMgGaO4. Phys. Rev. B 97, 125105 (2018).
Zhu, Z., Maksimov, P. A., White, S. R. & Cheryshev, A. L. Disorder-induced mimicry of a spin liquid in YbMgGaO4. Phys. Rev. Lett. 119, 157201 (2017).
Kimchi, I., Nahum, A. & Senthil, T. Valence bonds in random quantum magnets: theory and application to YbMgGaO4. Phys. Rev. X 8, 031028 (2018).
Ma, Z. et al. Spin-glass ground state in a triangular-lattice compound YbZnGaO4. Phys. Rev. Lett. 120, 087201 (2018).
Hashimoto, Y., Wakeshima, M. & Hinatsu, Y. Magnetic properties of ternary sodium oxides NaLnO2 (Ln = rare earths). J. Solid State Chem. 176, 266–272 (2003).
Liu, W. et al. Rare-earth chalcogenides: a large family of triangular lattice spin liquid candidates. Chin. Phys. Lett. 35, 117501 (2018).
Baenitz, M. et al. NaYbS2: a planar spin-1/2 triangular-lattice magnet and putative spin liquid. Phys. Rev. B 98, 220409(R) (2018).
Zeng, C. & Elser, V. Numerical studies of antiferromagnetism on a Kagomé net. Phys. Rev. B 42, 8436 (1990).
Chen, L. et al. Two-temperature scales in the triangular-lattice Heisenberg antiferromagnet. Phys. Rev. B 99, 140404(R) (2019).
Nambu, Y., Nakatsuji, S. & Maeno, Y. Coherent behavior and nonmagnetic impurity effects of spin disordered state in NiGa2S4. J. Phys. Soc. Jpn 75, 043711 (2006).
Gardner, J. S., Gingras, M. J. P. & Greedan, J. E. Magnetic pyrochlore oxides. Rev. Mod. Phys. 82, 53–107 (2010).
Wang, Y. R. Specific heat of a quantum Heisenberg model on a triangular lattice with two exchange parameters and its application to 3He adsorbed on graphite. Phys. Rev. B 45, 12608(R) (1992).
Isoda, M., Nakano, H. & Sakai, T. Specific heat and magnetic susceptibility of Ising-like anisotropic Heisenberg model on kagome lattice. J. Phys. Soc. Jpn 80, 084704 (2011).
Elstner, N. & Young, A. P. Spin-1/2 Heisenberg antiferromagnet on the kagomé lattice: high-temperature expansion and exact-diagonalization studies. Phys. Rev. B 50, 6871–6876 (1994).
Singh, R. R. P. & Oitmaa, J. High-temperature series expansion study of the Heisenberg antiferromagnet on the hyperkagome lattice: comparison with Na4Ir3O8. Phys. Rev. B 85, 104406 (2012).
Garlea, V. O. et al. Exotic magnetic field-induced spin-superstructures in a mixed honeycomb-triangular lattice system. Phys. Rev. X 9, 011038 (2019).
Iaconis, J., Liu, C., Haláz, G. B. & Balents, L. Spin liquid versus spin orbit coupling on the triangular lattice. SciPost Phys. 4, 003 (2018).
Zhu, Z., Maksimov, P. A., White, S. R. & Chernyshev, A. L. Topography of spin liquids on a triangular lattice. Phys. Rev. Lett. 120, 207203 (2018).
Starykh, O. A. Unusual ordered phases of highly frustrated magnets: a review. Rep. Prog. Phys. 78, 052502 (2015).
Chubokov, A. V. & Golosov, D. I. Quantum theory of an antiferromagnet on a triangular lattice in a magnetic field. J. Phys.: Condens. Matter 3, 69–82 (1991).
Ran, Y., Hermele, M., Lee, P. A. & Wen, X.-G. Projected-wave-function study of the spin-1/2 Heisenberg model on the Kagomé lattice. Phys. Rev. Lett. 98, 117205 (2007).
Rastelli, E. & Tassi, A. The rhombohedral Heisenberg antiferromagnet: infinite degeneracy of the ground state and magnetic properties of solid oxygen. J. Phys. C: Solid State Phys. 19, L423–L428 (1986).
Ono, T. et al. Magnetization plateaux of the S = 1/2 two-dimensional frustrated antiferromagnet Cs2CuBr4. J. Phys.: Condens. Matter 16, S773–S778 (2004).
Helton, J. S. et al. Spin dynamics of the spin-1/2 kagome lattice antiferromagnet ZnCu3(OH)6Cl2. Phys. Rev. Lett. 98, 107204 (2007).
Maryasin, V. S. & Zhitomirsky, M. E. Triangular antiferromagnet with nonmagnetic impurities. Phys. Rev. Lett. 111, 247201 (2013).
Rawl, R. et al. Ba8CoNb6O24: a spin-1/2 triangular-lattice Heisenberg antiferromagnet in the two-dimensional limit. Phys. Rev. B 95, 060412(R) (2017).
Cui, Y. et al. Mermin–Wagner physics, (H, T) phase diagram, and candidate quantum spin-liquid phase in the spin-1/2 triangular-lattice antiferromagnet Ba8CoNb6O24. Phys. Rev. Mater. 2, 044403 (2018).
Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B: Condens. Matter 192, 55–69 (1993).
Larson, A. C. & Von Dreele, R. B. General Structure Analysis System (GSAS) Report LAUR 86-748 (Los Alamos National Laboratory, 2004).
Toby, B. H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 34, 210–213 (2001).
Stoll, S. & Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 178, 42–55 (2006).
Acknowledgements
This work was supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under award DE-SC0017752 (S.D.W. and M.B.). M.B. acknowledges partial support by the National Science Foundation Graduate Research Fellowship Program under grant no. 1650114. Work by L.B. and C.L. was supported by the DOE, Office of Science, Basic Energy Sciences under award no. DE-FG02-08ER46524. Identification of commercial equipment does not imply recommendation or endorsement by NIST.
Author information
Authors and Affiliations
Contributions
M.B., S.D.W., C.L. and L.B. wrote the manuscript. M.B. and S.D.W. analysed experiment data and planned experiments. M.J.G. and E.K. performed susceptibility measurements. M.B. and T.H. performed heat capacity and magnetization measurements. C.L. and L.B. performed theoretical analysis of the material. C.B. performed the neutron diffraction measurements, and M.B. and N.P.B. performed inelastic neutron-scattering experiments. M.S., M.K., Y.L. and M.B. performed electron spin resonance measurements. M.B. and L.P. synthesized the materials.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary text, Figs. 1–5 and references.
Rights and permissions
About this article
Cite this article
Bordelon, M.M., Kenney, E., Liu, C. et al. Field-tunable quantum disordered ground state in the triangular-lattice antiferromagnet NaYbO2. Nat. Phys. 15, 1058–1064 (2019). https://doi.org/10.1038/s41567-019-0594-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0594-5
This article is cited by
-
Candidate spin-liquid ground state in CsNdSe2 with an effective spin-1/2 triangular lattice
Communications Materials (2024)
-
Realization of two-sublattice exchange physics in the triangular lattice compound Ba3Er(BO3)3
Communications Physics (2024)
-
Proximate spin liquid and fractionalization in the triangular antiferromagnet KYbSe2
Nature Physics (2024)
-
Quantum disordered ground state in the triangular-lattice magnet NaRuO2
Nature Physics (2023)
-
Chemical design of electronic and magnetic energy scales of tetravalent praseodymium materials
Nature Communications (2023)