Abstract
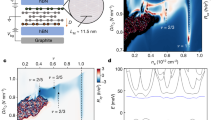
When a strong magnetic field is applied to a two-dimensional electron system, interactions between the electrons can cause fractional quantum Hall (FQH) effects1,2. Bringing two two-dimensional conductors close to each other, a new set of correlated states can emerge due to interactions between electrons in the same and opposite layers3,4,5,6. Here we report interlayer-correlated FQH states in a device consisting of two parallel graphene layers separated by a thin insulator. Current flow in one layer generates different quantized Hall signals in the two layers. This result is interpreted using composite fermion (CF) theory7 with different intralayer and interlayer Chern–Simons gauge-field couplings. We observe FQH states corresponding to integer values of CF Landau level (LL) filling in both layers, as well as ‘semiquantized’ states, where a full CF LL couples to a continuously varying partially filled CF LL. We also find a quantized state between two coupled half-filled CF LLs and attribute it to an interlayer CF exciton condensate.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author on reasonable request.
References
Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).
Halperin, B. I. Theory of the quantized Hall conductance. Helv. Phys. Acta 56, 75–104 (1983).
Chakraborty, T. & Pietiläinen, P. Fractional quantum Hall effect at half-filled Landau level in a multiple-layer electron system. Phys. Rev. Lett. 59, 2784–2787 (1987).
Eisenstein, J. Exciton condensation in bilayer quantum Hall systems. Annu. Rev. Condens. Matter Phys. 5, 159–181 (2014).
Jain, J. Composite Fermions (Cambridge Univ. Press, 2007).
Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).
Halperin, B. I. Statistics of quasiparticles and the hierarchy of fractional quantized Hall states. Phys. Rev. Lett. 52, 1583–1586 (1984).
Suen, Y. W., Engel, L. W., Santos, M. B., Shayegan, M. & Tsui, D. C. Observation of a ν = 1/2 fractional quantum Hall state in a double-layer electron system. Phys. Rev. Lett. 68, 1379–1382 (1992).
Eisenstein, J. P., Boebinger, G. S., Pfeiffer, L. N., West, K. W. & He, S. New fractional quantum Hall state in double-layer two-dimensional electron systems. Phys. Rev. Lett. 68, 1383–1386 (1992).
Kellogg, M., Spielman, I. B., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Observation of quantized Hall drag in a strongly correlated bilayer electron system. Phys. Rev. Lett. 88, 126804 (2002).
Liu, X., Watanabe, K., Taniguchi, T., Halperin, B. I. & Kim, P. Quantum Hall drag of exciton condensate in graphene. Nat. Phys. 13, 746–750 (2017).
Li, J. I., Taniguchi, T., Watanabe, K., Hone, J. & Dean, C. R. Excitonic superfluid phase in double bilayer graphene. Nat. Phys. 13, 751–755 (2017).
Kellogg, M., Eisenstein, J. Pv, Pfeiffer, L. N. & West, K. W. Vanishing Hall resistance at high magnetic field in a double-layer two-dimensional electron system. Phys. Rev. Lett. 93, 036801 (2004).
Tutuc, E., Shayegan, M. & Huse, D. A. Counterflow measurements in strongly correlated GaAs hole bilayers: evidence for electron-hole pairing. Phys. Rev. Lett. 93, 036802 (2004).
Spielman, I. B., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Resonantly enhanced tunneling in a double layer quantum Hall ferromagnet. Phys. Rev. Lett. 84, 5808–5811 (2000).
Yoshioka, D., MacDonald, A. H. & Girvin, S. M. Fractional quantum Hall effect in two-layered systems. Phys. Rev. B 39, 1932–1935 (1989).
Scarola, V. W. & Jain, J. K. Phase diagram of bilayer composite fermion states. Phys. Rev. B 64, 085313 (2001).
Barkeshli, M. & Wen, X.-G. Non-Abelian two-component fractional quantum Hall states. Phys. Rev. B 82, 233301 (2010).
Geraedts, S., Zaletel, M. P., Papić, Z. & Mong, R. S. K. Competing Abelian and non-Abelian topological orders in ν = 1/3 + 1/3 quantum Hall bilayers. Phys. Rev. B 91, 205139 (2015).
He, S., Das Sarma, S. & Xie, X. C. Quantized Hall effect and quantum phase transitions in coupled two-layer electron systems. Phys. Rev. B 47, 4394–4412 (1993).
Zibrov, A. A. et al. Tunable interacting composite fermion phases in a half-filled bilayer-graphene Landau level. Nature 549, 360–364 (2017).
Kellogg, M. J. Evidence for Excitonic Superfluidity in a Bilayer Two-Dimensional Electron System. PhD thesis, California Institute of Technology (2005).
Hill, N. P. R. et al. Frictional drag between parallel two-dimensional electron gases in a perpendicular magnetic field. J. Phys. Condens. Matter 8, L557–L562 (1996).
Acknowledgements
The major experimental work is supported by DOE (DE-SC0012260). The theoretical analysis was supported by the Science and Technology Center for Integrated Quantum Materials, NSF grant no. DMR-1231319. P.K. acknowledges partial support from the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant GBMF4543. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by MEXT, Japan, and CREST(JPMJCR15F3), JST. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement no. DMR-1157490* and the State of Florida. Nanofabrication was performed at the Center for Nanoscale Systems at Harvard, supported in part by NSF NNIN award ECS-00335765. In preparation of this manuscript, we are aware of related work done by J. I. A. Li et al. We thank B. Rosenow, J. I. A. Li and C. Dean for helpful discussions.
Author information
Authors and Affiliations
Contributions
X.L. and P.K. conceived the experiment. X.L. and Z.H. fabricated the samples and performed the measurements. X.L. analysed the data. B.H. conducted the theoretical analysis. X.L., B.I.H. and P.K. wrote the paper. K.W. and T.T. supplied hBN crystals.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Physics thanks Timo Hyart, Emanuel Tutuc and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Additional theoretical details, Supplementary Figs. 1–4 and Supplementary references 1–12.
Rights and permissions
About this article
Cite this article
Liu, X., Hao, Z., Watanabe, K. et al. Interlayer fractional quantum Hall effect in a coupled graphene double layer. Nat. Phys. 15, 893–897 (2019). https://doi.org/10.1038/s41567-019-0546-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-019-0546-0
This article is cited by
-
Time-reversal even charge hall effect from twisted interface coupling
Nature Communications (2023)
-
Signature of quantum interference effect in inter-layer Coulomb drag in graphene-based electronic double-layer systems
Nature Communications (2023)
-
Strain-induced quantum Hall phenomena of excitons in graphene
Scientific Reports (2022)
-
Excitonic insulator in a heterojunction moiré superlattice
Nature Physics (2022)
-
Size dependence- and induced transformations- of fractional quantum Hall effects under tilted magnetic fields
Scientific Reports (2022)