Abstract
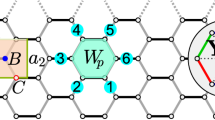
Quantum spin liquid is a disordered but highly entangled magnetic state with fractional spin excitations1. The ground state of an exactly solved Kitaev honeycomb model is perhaps its clearest example2. Under a magnetic field, a spin flip in this model fractionalizes into two types of anyon, a quasiparticle with more complex exchange statistics than standard fermions or bosons: a pair of gauge fluxes and a Majorana fermion2,3. Here, we demonstrate this kind of fractionalization in the Kitaev paramagnetic state of the honeycomb magnet α-RuCl3. The spin excitation gap determined by nuclear magnetic resonance consists of the predicted Majorana fermion contribution following the cube of the applied magnetic field2,4,5, and a finite zero-field contribution matching the predicted size of the gauge flux gap2,6. The observed fractionalization into gapped anyons survives in a broad range of temperatures and magnetic fields, which establishes α-RuCl3 as a unique platform for future investigations of anyons.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017).
Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Baskaran, G., Mandal, S. & Shankar, R. Exact results for spin dynamics and fractionalization in the Kitaev model. Phys. Rev. Lett. 98, 247201 (2007).
Jiang, H.-C., Gu, Z.-C., Qi, X.-L. & Trebst, S. Possible proximity of the Mott insulating iridate Na2IrO3 to a topological phase: phase diagram of the Heisenberg-Kitaev model in a magnetic field. Phys. Rev. B 83, 245104 (2011).
Nasu, J., Yoshitake, J. & Motome, Y. Thermal transport in the Kitaev model. Phys. Rev. Lett. 119, 127204 (2017).
Knolle, J., Kovrizhin, D. L., Chalker, J. T. & Moessner, R. Dynamics of a two-dimensional quantum spin liquid: signatures of emergent Majorana fermions and fluxes. Phys. Rev. Lett. 112, 207203 (2014).
de-Picciotto, R. et al. Direct observation of a fractional charge. Nature 389, 162–164 (1997).
Jompol, Y. et al. Probing spin-charge separation in a Tomonaga-Luttinger liquid. Science 325, 597–601 (2009).
Castelnovo, C., Moessner, R. & Sondhi, S. L. Magnetic monopoles in spin ice. Nature 451, 42–45 (2008).
Han, T.-H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).
Paddison, J. A. M. et al. Continuous excitations of the triangular-lattice quantum spin liquid YbMgGaO4. Nat. Phys. 13, 117–122 (2017).
Nasu, J., Knolle, J., Kovrizhin, D. L., Motome, Y. & Moessner, R. Fermionic response from fractionalization in an insulating two-dimensional magnet. Nat. Phys. 12, 912–915 (2016).
Nasu, J., Udagawa, M. & Motome, Y. Thermal fractionalization of quantum spins in a Kitaev model: temperature-linear specific heat and coherent transport of Majorana fermions. Phys. Rev. B 92, 115122 (2015).
Sandilands, L. J., Tian, Y., Plumb, K. W., Kim, Y.-J. & Burch, K. S. Scattering continuum and possible fractionalized excitations in α-RuCl3. Phys. Rev. Lett. 114, 147201 (2015).
Banerjee, A. et al. Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet. Nat. Mater. 15, 733–740 (2016).
Banerjee, A. et al. Neutron scattering in the proximate quantum spin liquid α-RuCl3. Science 356, 1055–1059 (2017).
Do, S.-H. et al. Majorana fermions in the Kitaev quantum spin system α-RuCl3. Nat. Phys. 13, 1079–1084 (2017).
Choi, S. K. et al. Spin waves and revised crystal structure of honeycomb iridate Na2IrO3. Phys. Rev. Lett. 108, 127204 (2012).
Singh, Y. et al. Relevance of the Heisenberg-Kitaev model for the honeycomb lattice iridates A 2IrO3. Phys. Rev. Lett. 108, 127203 (2012).
Plumb, K. W. et al. α-RuCl3: a spin-orbit assisted Mott insulator on a honeycomb lattice. Phys. Rev. B 90, 041112(R) (2014).
Jackeli, G. & Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 102, 017205 (2009).
Kubota, Y., Tanaka, H., Ono, T., Narumi, Y. & Kindo, K. Successive magnetic phase transitions in α-RuCl3: XY-like frustrated magnet on the honeycomb lattice. Phys. Rev. B 91, 094422 (2015).
Majumder, M. et al. Anisotropic Ru3+ 4d 5 magnetism in the α-RuCl3 honeycomb system: susceptibility, specific heat, and zero-field NMR. Phys. Rev. B 91, 180401(R) (2015).
Cao, H. B. et al. Low-temperature crystal and magnetic structure of α-RuCl3. Phys. Rev. B 93, 134423 (2016).
Johnson, R. D. et al. Monoclinic crystal structure of α-RuCl3 and the zigzag antiferromagnetic ground state. Phys. Rev. B 92, 235119 (2015).
Yadav, R. et al. Kitaev exchange and field-induced quantum spin-liquid states in honeycomb α-RuCl3. Sci. Rep. 6, 37925 (2016).
Yoshitake, J., Nasu, J. & Motome, Y. Fractional spin fluctuations as a precursor of quantum spin liquids: Majorana dynamical mean-field study for the Kitaev model. Phys. Rev. Lett. 117, 157203 (2016).
Yoshitake, J., Nasu, J. & Motome, Y. Temperature evolution of spin dynamics in two- and three-dimensional Kitaev models: influence of fluctuating Z 2 flux. Phys. Rev. B 96, 064433 (2017).
Ran, K. et al. Spin-wave excitations evidencing the Kitaev interaction in single crystalline α-RuCl3. Phys. Rev. Lett. 118, 107203 (2017).
Banerjee, A. et al. Excitations in the field-induced quantum spin liquid state of α-RuCl3. npj Quant. Mater. 3, 8 (2018).
Zheng, J. et al. Gapless spin excitations in the field-induced quantum spin liquid phase of α-RuCl3. Phys. Rev. Lett. 119, 227208 (2017).
Baek, S.-H. et al. Evidence for a field-induced quantum spin liquid in α-RuCl3. Phys. Rev. Lett. 119, 037201 (2017).
Sears, J. A., Zhao, Y., Xu, Z., Lynn, J. W. & Kim, Y.-J. Phase diagram of α-RuCl3 in an in-plane magnetic field. Phys. Rev. B 95, 180411(R) (2017).
Hentrich, R. et al. Unusual phonon heat transport in α-RuCl3: strong spin-phonon scattering and field-induced spin gap. Phys. Rev. Lett. 120, 117204 (2018).
Ponomaryov, A. N. et al. Unconventional spin dynamics in the honeycomb-lattice material α-RuCl3: high-field electron spin resonance studies. Phys. Rev. B 96, 241107(R) (2017).
Wolter, A. U. B. et al. Field-induced quantum criticality in the Kitaev system α-RuCl3. Phys. Rev. B 96, 041405(R) (2017).
Winter, S. M., Li, Y., Jeschke, H. O. & Valentí, R. Challenges in design of Kitaev materials: magnetic interactions from competing energy scales. Phys. Rev. B 93, 214431 (2016).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Abragam, A. Principles of Nuclear Magnetism (Oxford Univ. Press, Oxford, 2011).
Jeong, M. et al. Attractive Tomonaga-Luttinger liquid in a quantum spin ladder. Phys. Rev. Lett. 111, 106404 (2013).
Klanjšek, M. et al. Phonon-modulated magnetic interactions and spin Tomonaga-Luttinger liquid in the p-orbital antiferromagnet CsO2. Phys. Rev. Lett. 115, 057205 (2015).
Horvatić, M. & Berthier, C. in High Magnetic Fields: Applications in Condensed Matter Physics and Spectroscopy (eds Berthier, C. et al.) 191–210 (Vol. 595, Lecture Notes in Physics, Springer, Berlin, 2002).
Moriya, T. Nuclear magnetic relaxation in antiferromagnetics. Prog. Theor. Phys. 16, 23–44 (1956).
Beeman, D. & Pincus, P. Nuclear spin-lattice relaxation in magnetic insulators. Phys. Rev. 166, 359–375 (1968).
Acknowledgements
M.K. acknowledges discussions with M. Horvatić and C. Berthier. The work was partly supported by the Slovenian ARRS program No. P1-0125 and project No. PR-07587. A.B. and Ch.R. acknowledge financial support by the Marie Curie FP7 COFUND PSI Fellowship programme, the Swiss National Science Foundation (Sinergia Network Mott Physics Beyond the Heisenberg Model), and the ERC Grant Hyper Quantum Criticality (HyperQC).
Author information
Authors and Affiliations
Contributions
M.K. conceived, designed and led the project. N.J. and M.K. performed the NMR experiments and analysed the data. K.W.K. and D.B. grew the samples. A.B. performed the magnetic susceptibility measurements. All the authors discussed the results. M.K. wrote the paper with feedback from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figures 1–9, Supplementary References
Rights and permissions
About this article
Cite this article
Janša, N., Zorko, A., Gomilšek, M. et al. Observation of two types of fractional excitation in the Kitaev honeycomb magnet. Nature Phys 14, 786–790 (2018). https://doi.org/10.1038/s41567-018-0129-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-018-0129-5
This article is cited by
-
Possible intermediate quantum spin liquid phase in α-RuCl3 under high magnetic fields up to 100 T
Nature Communications (2023)
-
Identification of a Kitaev quantum spin liquid by magnetic field angle dependence
Nature Communications (2022)
-
Signature of a randomness-driven spin-liquid state in a frustrated magnet
Communications Physics (2022)
-
Theory of the Kitaev model in a [111] magnetic field
Nature Communications (2022)
-
Evidence for a spinon Kondo effect in cobalt atoms on single-layer 1T-TaSe2
Nature Physics (2022)