Abstract
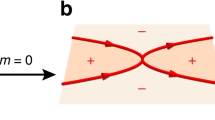
Three-dimensional Weyl and Dirac nodal points1 have attracted widespread interest across multiple disciplines and in many platforms but allow for few structural variations. In contrast, nodal lines2,3,4 can have numerous topological configurations in momentum space, forming nodal rings5,6,7,8,9, nodal chains10,11,12,13,14,15, nodal links16,17,18,19,20 and nodal knots21,22. However, nodal lines are much less explored because of the lack of an ideal experimental realization23,24,25. For example, in condensed-matter systems, nodal lines are often fragile to spin–orbit coupling, located away from the Fermi level, coexist with energy-degenerate trivial bands or have a degeneracy line that disperses strongly in energy. Here, overcoming all these difficulties, we theoretically predict and experimentally observe nodal chains in a metallic-mesh photonic crystal having frequency-isolated linear band-touching rings chained across the entire Brillouin zone. These nodal chains are protected by mirror symmetry and have a frequency variation of less than 1%. We use angle-resolved transmission measurements to probe the projected bulk dispersion and perform Fourier-transformed field scans to map out the dispersion of the drumhead surface state. Our results establish an ideal nodal-line material for further study of topological line degeneracies with non-trivial connectivity and consequent wave dynamics that are richer than those in Weyl and Dirac materials.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three dimensional solids. Preprint at https://arxiv.org/abs/1705.01111 (2017).
Burkov, A. A., Hook, M. D. & Balents, L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011).
Lu, L., Fu, L., Joannopoulos, J. D. & Soljacic, M. Weyl points and line nodes in gyroid photonic crystals. Nat. Photon. 7, 294–299 (2013).
Fang, C., Weng, H., Dai, X. & Fang, Z. Topological nodal line semimetals. Chin. Phys. B 25, 117106 (2016).
Lu, L. et al. Experimental observation of Weyl points. Science 349, 622–624 (2015).
Kim, Y., Wieder, B. J., Kane, C. L. & Rappe, A. M. Dirac line nodes in inversion-symmetric crystals. Phys. Rev. Lett. 115, 036806 (2015).
Yu, R., Weng, H., Fang, Z., Dai, X. & Hu, X. Topological node-line semimetal and Dirac semimetal state in antiperovskite Cu3PdN. Phys. Rev. Lett. 115, 036807 (2015).
Fang, C., Chen, Y., Kee, H.-Y. & Fu, L. Topological nodal line semimetals with and without spin–orbital coupling. Phys. Rev. B 92, 081201 (2015).
Kobayashi, S. et al. Crossing-line-node semimetals: general theory and application to rare-earth trihydrides. Phys. Rev. B 95, 245208 (2017).
Weng, H. et al. Topological node-line semimetal in three-dimensional grapheme networks. Phys. Rev. B 92, 045108 (2015).
Bzdusek, T., Wu, Q., Riiegg, A., Sigrist, M. & Soluyanov, A. A. Nodal-chain metals. Nature 538, 75–78 (2016).
Kawakami, T. & Hu, X. Symmetry-guaranteed and accidental nodal-line semimetals in fcc lattice. Preprint at https://arxiv.org/abs/1611.07342 (2016).
Yu, R., Wu, Q., Fang, Z. & Weng, H. From nodal chain semimetal to Weyl semimetal in HfC. Phys. Rev. Lett. 119, 036401 (2017).
Wang, S.-S., Liu, Y., Yu, Z.-M., Sheng, X.-L. & Yang, S. A. Hourglass Dirac chain metal in rhenium dioxide. Preprint at https://arxiv.org/abs/1705.01424 (2017).
Feng, X., Yue, C., Song, Z., Wu, Q. & Wen, B. Topological Dirac nodal-net fermions in AlB2-type TiB2 and ZrB2. Preprint at https://arxiv.org/abs/1705.00511 (2017).
Chen, W., Lu, H.-Z. & Hou, J.-M. Topological semimetals with a double-helix nodal link. Phys. Rev. B 96, 041102 (2017).
Yan, Z. et al. Nodal-link semimetals. Phys. Rev. B 96, 041103 (2017).
Chang, P.-Y. & Yee, C.-H. Weyl-link semimetals. Phys. Rev. B 96, 081114 (2017).
Zhong, C. et al. Three-dimensional pentagon carbon with a genesis of emergent fermions. Nat. Commun. 8, 15641 (2017).
Chang, G. et al. Topological Hopf and chain link semimetal states and their application to Co2MnGa. Phys. Rev. Lett. 119, 156401 (2017).
Ezawa, M. Topological semimetals carrying arbitrary Hopf numbers: Fermi surface topologies of a Hopf link, Solomon's knot, trefoil knot, and other linked nodal varieties. Phys. Rev. B 96, 041202 (2017).
Bi, R., Yan, Z., Lu, L. & Wang, Z. Nodal-knot semimetals. Phys. Rev. B 96, 201305 (2017).
Bian, G. et al. Topological nodal-line fermions in spin–orbit metal PbTaSe2. Nat. Commun. 7, 10556 (2016).
Schoop, L. M. et al. Dirac cone protected by non-symmorphic symmetry and three-dimensional Dirac line node in Zr-SiS. Nat. Commun. 7, 11696 (2016).
Chen, C. et al. Dirac line nodes and effect of spin–orbit coupling in the nonsymmorphic critical semimetals MSiS (M = Hf, Zr). Phys. Rev. B 95, 125126 (2017).
Pendry, J. B., Holden, A. J., Stewart, W. J. & Youngs, I. Extremely low frequency plasmons in metallic mesostructures. Phys. Rev. Lett. 76, 4773 (1996).
Shapiro, M. A., Sirigiri, J. R., Temkin, R. J. & Shvets, G. 3D metallic lattices for accelerator applications. In Proceedings of the Particle Accelerator Conference, 2005. PAC 2005 1838–1840 (IEEE, 2005).
Chen, W.-J. & Chan, C. T. Metamaterials with index ellipsoids at arbitrary k-points. Preprint at https://arxiv.org/abs/1611.08099 (2016).
Ye, D., Lu, L., Joannopoulos, J. D., Soljacic, M. & Ran, L. Invisible metallic mesh. Proc. Natl Acad. Sci.USA 113, 2568–2572 (2016).
Liu, B., Johnson, S. G., Joannopoulos, J. D. & Lu, L. Generalized Gilat–Raubenheimer method for density-of-states calculation in photonic crystals. Preprint at https://arxiv.org/abs/1711.07993 (2017).
Acknowledgements
We thank Yang He, Chen Fang and Hongming Weng for discussions. The authors were supported by the National Key R&D Program of China under Grant Nos 2017YFA0303800 and 2016YFA0302400 and by NSFC under Project Nos 11721404 (L.L.), 11674189 (Z.Y., Z.W.), 61625502 (H.C.), 61574127 (H.C.), the Top-Notch Young Talents Program (H.C.) and the National Thousand Young Talents Program (L.L.) of China.
Author information
Authors and Affiliations
Contributions
L.L. proposed and led the project. R.L. fabricated the sample. Q.Y. and R.L. made the measurements. Q.Y. processed the data and carried out the calculations. Z.W. and Z.Y. came up with the k.p model and enhanced the theoretical understanding. All authors contributed to the discussion and writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Five figures with additional description and discussions.
Rights and permissions
About this article
Cite this article
Yan, Q., Liu, R., Yan, Z. et al. Experimental discovery of nodal chains. Nature Phys 14, 461–464 (2018). https://doi.org/10.1038/s41567-017-0041-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-017-0041-4
This article is cited by
-
Experimental observation of multiple topological nodal structure in LaSb2
Science China Physics, Mechanics & Astronomy (2024)
-
Symmetry-protected topological exceptional chains in non-Hermitian crystals
Communications Physics (2023)
-
Antichiral surface states in time-reversal-invariant photonic semimetals
Nature Communications (2023)
-
Observation of bulk quadrupole in topological heat transport
Nature Communications (2023)
-
Symmetry-enforced nodal chain phonons
npj Quantum Materials (2022)