Introduction

Topological quasiparticles, emerged around band degeneracy points in condensed matters, have been attracting tremendous research interest in the past decade. The field was initiated with a focus on electronic systems. Pioneering examples include electrons around Weyl1,2,3,4 and Dirac4,5,6,7,8 points in the band structures, which resemble Weyl and Dirac fermions and thereby can simulate fascinating effects from high energy physics9,10,11. Moreover, condensed matter systems respect the space group (SG) symmetry, which is a much smaller subgroup of the Poincaré symmetry. The reduced constraints permit a rich variety of emergent quasiparticles beyond the Weyl/Dirac paradigm12,13,14,15. For instance, band degeneracies may form higher-dimensional manifolds in the momentum space, leading to nodal-line7,16,17,18,19,20,21,22,23,24,25 and even nodal-surface26,27,28,29 electrons, with topological boundary modes and effects.

It was later realized that this research can be naturally extended to bosonic and even classical systems. Particularly, there is a surge of interest recently in exploring quasiparticles in phonons30,31,32,33,34,35,36, which describe the atomic lattice vibrations in solids. This is also motivated by the advance in experimental techniques which can now probe the full THz phonon spectrum with meV-resolution37,38,39. A number of materials with Weyl, Dirac, and nodal-line phonons have been predicted40,41,42,43,44,45,46,47, and some have been successfully verified in experiment43,48. As direct extensions of corresponding concepts from electronic systems, except for the particles statistics, most of these phonons share essentially the same features as their electronic counterparts.

In this work, we try to find topological phonons with a character limited to phononic systems. Specifically, we present such an example - the symmetry-enforced nodal-chain phonons.

A nodal chain is composed of multiple nodal rings touching at isolated points and is extended in momentum space (e.g., see Fig. 1). The concept was initially studied also in electronic systems, where the electronic nodal chains usually require complicated non-symmorphic crystal symmetries to be robust against spin-orbit coupling (SOC)49,50. Nodal chains with symmorphic symmetries were also discussed51,52,53,54, but they are typically destroyed by SOC, and more importantly, they are not symmetry enforced, meaning that their presence in the spectrum depends on the system details and is not guaranteed.

Fig. 1: Symmetry-enforced nodal chains for the five candidates SGs.
figure 1

a SG 121, 139, and 140 host nodal chains running along the fourfold S4z axis. b In SG 225 and 226, there are chains running along all three directions, forming a network structure. Here, the rings with different orientations are marked with different colors.

Full size image

In this work, we find a class of nodal-chain phonons that are enforced by symmorphic symmetries. We show that in five SGs, such phonons are enforced by the D2d little co-group and its vector representation at a non-time-reversal-invariant-momentum (non-TRIM) point O. The key point is: Unlike electrons and other systems, where the basis at lattice sites can take different symmetries (e.g., s, p, d, etc.), for phonons, the lattice displacement at each site is a vector. For the five SGs, modes with the vector representation at O are guaranteed to exist due to the real-space vector basis symmetry. Therefore, the nodal chain is guaranteed to exist in these space groups. In addition, the vulnerability under SOC is not an issue here, since phonons are intrinsically spinless. In this sense, the proposed symmetry-enforced nodal chain indeed manifests characters for phononic systems. Interestingly, depending on the SG, there are two different nodal-chain patterns, as shown in Fig. 1. Guided by the symmetry condition, we propose that K2O, an existing material, is a candidate with almost ideal nodal chain phonons. We show that the LO-TO splitting55 helps to expose the phononic nodal chain in K2O as the only band degeneracy in a large frequency window, facilitating the experimental detection. In addition, due to the spacetime inversion symmetry \({{{\mathcal{PT}}}}\), each ring in the chain enjoys additional protection by the π Berry phase56, which also leads to the protected drumhead surface phonon modes8,17 on multiple surfaces of a sample.

Results

Symmetry condition

First, we propose a formation mechanism for the phononic nodal chain. We show that the D2d group with its vector representation at a non-TRIM point of the Brillouin zone (BZ) enforces the existence of a chain. The D2d group contains two mutually orthogonal mirrors, which we may denote as Mx and My, and a fourfold roto-reflection S4z, which connects the two mirrors. Assume that D2d is the little co-group (or its subgroup) at a non-TRIM point O in the BZ, and the qz axis through O corresponds to the S4z axis, as shown in Fig. 2a.

Fig. 2: Schematic diagram for a nodal chain.
figure 2

a Schematic diagram for a nodal chain formed by two rings located in two mutually orthogonal mirror planes Mx and My. O is a non-TRIM point with D2d little co-group. b Spectrum along the qz axis for a pair of phonon branches that correspond to the E representation of D2d at O. mi (i = x, y) are the mirror eigenvalues. c An arbitrary path ℓ in the Mx plane, which connects a point R on the qz axis to its S4z image \(R^{\prime}\). The spectrum along ℓ is shown in (d), where the two branches must still cross at some point Q, as they have opposite mx eigenvalues. The crossing point traces out a ring in the Mx plane, as shown in (c).

Full size image

Consider the modes at O which correspond to the two-dimensional vector irreducible representation E of D2d. These modes transform as vectors lying in the plane normal to the S4z axis. They form twofold degenerate pairs at O (each pair corresponding to the E representation). Let us consider one such degenerate pair. Since [Mx, My] = 0, the two states can be chosen as simultaneous eigenstates of the two mirrors, and they must have opposite Mx as well as My eigenvalues. If we denote one state as \(\left|{m}_{x},{m}_{y}\right\rangle\) with mx/y ∈ {+1, −1} the mirror eigenvalues, then the other state must be \(\left|{\overline{m}}_{x},{\overline{m}}_{y}\right\rangle\), where \({\overline{m}}_{i}\equiv -{m}_{i}\). In the subspace of this pair, the symmetry operations satisfy the following relations

$$\{{{{{\mathcal{M}}}}}_{x},{{{{\mathcal{S}}}}}_{4z}\}=0,\quad \{{{{{\mathcal{M}}}}}_{y},{{{{\mathcal{S}}}}}_{4z}\}=0.$$
(1)

Here, the script symbols denote the symmetry operators represented in the subspace.

When moving along the qz axis away from O, the degenerate pair will generally split. However, the symmetries Mx and My are preserved on the qz axis. Consider the spectrum of the two branches on the qz axis. First, it must be symmetric with respect to O, since the spectrum at point (0, 0, qz) is connected to that at (0, 0, −qz) by S4z. Second, due to Eq. (1), the two states connected by S4z at (0, 0, ±qz) with the same energy must have opposite mx and my values. This is schematically illustrated in Fig. 2b, showing that the two branches with opposite mi (i = x, y) cross each other at O.

Now, consider an arbitrary path ℓ in the Mx plane, which connects a point R, say at (0, 0, π/2), to its S4z image \(R^{\prime}\) at (0, 0, −π/2) [see Fig. 2c]. Since ℓ is in the Mx plane, mx for states on the path is still well defined. Meanwhile, because the mx eigenvalues are flipped between R and \(R^{\prime}\), the two phonon branches that we studied above must also cross each other at some point Q on the path ℓ, as illustrated in Fig. 2c, d. Since ℓ is arbitrary, the crossing point must trace out a nodal ring passing through O and lying in the Mx plane. The same argument applies to the My plane and results in another nodal ring. The two rings are perpendicular to each other, touch at point O [and also at (0, 0, ±π) which is another D2d-invariant point], and are connected by S4z. Therefore, they compose a nodal chain in the momentum space running along the S4z axis, as illustrated in Fig. 2a.

We have a few remarks. First, we required point O to be a non-TRIM point. The reason is that if it is a TRIM point, then the time-reversal symmetry \({{{\mathcal{T}}}}\) and S4z would require the two branches that are degenerate at O remain degenerate on the qz axis. In this case, we have only a single phononic nodal line, rather than a chain.

Second, the touching of two perpendicular rings at the O point can also be inferred from the k ⋅ p effective model expanded at O. Constrained by the D2d group and on the E basis, we obtain the following effective model expanded to q-quadratic order

$${{{{\mathcal{H}}}}}_{{{\mbox{eff}}}}({{{\bf{q}}}})=\epsilon ({{{\bf{q}}}}){\sigma }_{0}+{c}_{1}{q}_{x}{q}_{y}{\sigma }_{x}+[{c}_{2}{q}_{z}+{c}_{3}({q}_{x}^{2}-{q}_{y}^{2})]{\sigma }_{z},$$
(2)

where \(\epsilon ({{{\bf{q}}}})={\varepsilon }_{1}({q}_{x}^{2}+{q}_{y}^{2})+{\varepsilon }_{2}{q}_{z}^{2}\), εi and ci are real model parameters, and σ’s are Pauli matrices. The model shows a linear band splitting along qz and quadratic splitting in the qx-qy plane. The degeneracy manifold indeed conforms with that of two orthogonal nodal rings (see details in the Supplementary Information).

Third, the analysis above applies only to spinless particles. For spinful ones like electrons, the SOC will generally destroy the nodal chain51.

Candidate space groups

Based on the proposed symmetry conditions above, we search for the candidate SGs through the 230 SGs. For each SG, we examine the little co-group for each non-TRIM high-symmetry point and check whether it contains D2d as a subgroup. This screening results in 10 SGs, including SG 121, 122, 139, 140, 141, 142, 225, 226, 227, and 228.

After obtaining these SGs, we further check whether our proposed symmetry conditions are indeed fulfilled in these SGs. This is necessary because of two reasons. First, point O is not at the BZ center. The fractional translation in the certain non-symmorphic operations of the SG may alter the symmetry algebra at such a point. Second, depending on the SG, there may be some additional symmetry, particularly some magnetic symmetry (of the form \(U{{{\mathcal{T}}}}\) with U a spatial operation), at point O, which may affect the formation of the nodal chain. This process removes five of the ten SGs, for which the nodal chain would reduce to a straight nodal line along the S4z axis due to additional non-symmorphic operations. The remaining five candidates SGs are listed in Table 1.

Table 1 SGs hosting the proposed symmetry-enforced nodal-chain phonons.
Full size table

Among the five candidates SGs in Table 1, by using the MKVEC tool57,58,59,60,61, we find that for SG 121, the magnetic little co-group at O is −42 m, which is just D2d. Meanwhile, for the other four SGs, the magnetic little co-group at O is \(4^{\prime} /m^{\prime} m^{\prime} m\), which is a supergroup of D2d and contains the extra magnetic symmetry of \({{{\mathcal{PT}}}}\). Nevertheless, we verify that the extra \({{{\mathcal{PT}}}}\) symmetry does not affect the existence of the nodal chain in these SGs. The information of crystal system and the corresponding point O are also given in Table 1.

Next, we check that for these five SGs, the required vector representation at O must exist due to the real-space vector basis symmetry. Specifically, for each SG candidate, by using the BANDREP tool62,63,64, we examine the representations at O induced by the (real-space) vector basis at all possible Wyckoff positions in a unit cell (see the Supplementary Information for details)62. Through this process, we confirm that the required vector representation and hence the nodal chain are guaranteed to appear in these five SGs. Clearly, from the analysis, the symmetry enforcement here originated from the vector basis symmetry of phononic systems. This symmetry enforcement mechanism is the most important characteristics of our proposed topological phonons.

Interestingly, the five SGs can give two different patterns of the nodal chains, as illustrated in Fig. 1. One observes that the chains in SG 121, 139, and 140 form a one-dimensional structure running along the S4z axis. In comparison, there are three families of orthogonal chains for SG 225 and 226, forming a three-dimensional chain network.

In addition, we note that except for SG 121, the groups in Table 1 possess the inversion symmetry \({{{\mathcal{P}}}}\). Then for these SGs, the combined \({{{\mathcal{PT}}}}\) symmetry enforces a π-quantized Berry phase for arbitrarily closed loops in momentum space, constituting a one-dimensional \({{\mathbb{Z}}}_{2}\) topological charge for \({{{\mathcal{PT}}}}\)-invariant systems. For SGs with mirror or certain rotation symmetries, the Berry phase can also be quantized on some loop, if the symmetry operation reverses the momentum on the loop. This offers the nodal rings additional protection, namely, each ring is protected by the π Berry phase defined on a small loop encircling the ring. As a result, even when the symmetry is reduced by certain perturbations on the system, each ring should persist as long as \({{{\mathcal{PT}}}}\) is still preserved.

Nodal-chain phonons in K2O

Guided by the symmetry condition, we identify an existing material K2O as a candidate with almost ideal nodal-chain phonons. The K2O crystal was synthesized long ago in the 1930s65. As shown in Fig. 3a, it has the antifluorite crystal structure with the SG 225 (\(Fm\bar{3}m\)), which is one of the candidates in Table 1. We investigate its properties by using the first-principles calculations based on the density functional theory (DFT). The calculation details are presented in the Methods. The optimized conventional lattice constant is a = 6.49 Å, which agrees well with the experimental value of 6.44 Å65. The two types of atoms K and O occupy the 8c and 4a Wyckoff positions, respectively.

Fig. 3: Calculated phonon spectrum and phonon density of states for K2O.
figure 3

a Conventional unit cell and (b) primitive cell of K2O. c Calculated phonon spectrum and phonon density of states for K2O. The arrows indicate points on the nodal chain. d Calculated phonon spectrum and phonon density of states with non-analytic correction (LO-TO splitting) included.

Full size image

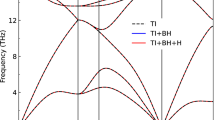
The calculated phonon spectrum of K2O is plotted in Fig. 3c. According to Table 1 and Fig. 1b, for SG 225, the ring touching point O corresponds to the W point of the BZ, and there are three mutually orthogonal rings, forming a network of chains in the extended BZ. In Fig. 3c, a chain at around 7 THz formed by two optical branches can be clearly observed (indicated by the red arrows). A careful scan of the BZ confirms that the crossing between the top two branches forms the chain pattern consistent with Fig. 1b.

Notably, in Fig. 3c, the phonon band structure around the chain is not very “clean”, because the top phonon branch bends down near the BZ center. Fortunately, this is remedied by including the non-analytic correction from long-range Coulomb interactions, which is typically pronounced for ionic crystals such as K2O. This correction leads to the well-known energy splitting between longitudinal optical and transverse optical phonon branches near the BZ center, i.e., the LO-TO splitting. In Fig. 3d, one observes that the correction results in a large LO-TO splitting and pushes up the top branch. Meanwhile, the dispersion around the chain is more or less unaffected. Consequently, the phononic nodal chain is now well exposed in a large frequency window with a width ~1 THz. The energy of the chain can be readily inferred from the dip in the phonon density of states.

The phononic nodal chain here is guaranteed to exist in the spectrum, associated with the vector representation induced by the real-space vector basis. It should be noted that there are also other induced representations presenting at the same time, and the corresponding phonon branches do not form nodal chains. This is the case for the bands around 5 THz in Fig. 3.

The clean band structure, the relatively large frequency window, and the small energy variation on the chain make K2O an almost ideal candidate for experimental studies of our proposed symmetry-enforced nodal-chain phonons.

Topological surface phonon modes

We have mentioned that owing to the \({{{\mathcal{PT}}}}\) symmetry, each ring of the chain features a quantized π Berry phase. It follows that the Zak phase, defined as the Berry phase along a straight line traversing the BZ, must change by π when the line crosses a ring. The π Zak phase is verified by our first-principles calculations, as indicated in Fig. 4a. It leads to the protected drumhead-like surface modes, which span the region in the surface BZ bounded by the projection of the ring.

Fig. 4: Calculated surface phonon spectrum for the (001) surface of K2O.
figure 4

a K2O’s BZ and the corresponding (001) surface BZ. A straight path passing through the nodal ring has a π Zak phase. This leads to protected drumhead surface modes. Here, we only show the ring in the horizontal plane. The analysis also applies to the other rings of the chain. b Calculated surface phonon spectrum for the (001) surface of K2O (without non-analytic correction). The arrows indicate the drumhead surface phonon modes.

Full size image

In Fig. 4b, we plot the calculated surface phonon spectrum for the (001) surface of K2O. One indeed finds the drumhead surface phonon modes, as indicated by the arrows. Drumhead surface modes also exist for conventional nodal-ring states, but they typically exist only on particular surfaces. For example, when the ring is parallel to the (001) surface, it is not going to produce drumhead surface modes on (100) and (010) surfaces. In comparison, since a nodal chain here is composed of orthogonal nodal rings, it must have drumhead surface modes simultaneously on multiple surfaces.

Discussion

We have revealed a topological phonon state that manifests the features of phononic systems, namely, it is enforced to exist by the vector basis symmetry of phonons. With this understanding, our work will open the direction to explore more types of topological phonons that are enforced by the basis of symmetry.

As mentioned in the introduction part, there are also other types of nodal chains in both spinless and spinful systems. For example, ref. 53 reported a spinless nodal chain in the electronic band structures of some honeycomb layered structures. Different from our case, the ring contact point (O point) there is not fixed on a high-symmetry point but can move on a high-symmetry path; and more importantly, the chain there is not symmetry enforced but is of accidental type.

It should be noted that although our proposed phononic nodal chain is guaranteed to exist in certain SGs, its energy and dispersion still depend on the details of the system. Hence, identifying experimentally favorable material candidates still requires extensive effort and a degree of luck. Nevertheless, the symmetry conditions revealed here to provide useful guidance for the material search. Besides K2O, we also identified a few other example materials, including Ge2Zn4Se8 (SG 121), Te2O4Tb4 (SG 139), and Ag4Tl4I8 (SG 140), with the help of the phonon database 47.

In an experiment, the bulk phonon dispersion can be imaged by inelastic x-ray scattering (IXS)37,38,39 or neutron scattering66. The surface phonon modes can be probed by the high-resolution electron energy loss spectroscopy67, helium scattering68, or THz spectroscopy69,70. Particularly, recent experiments with inelastic x-ray scattering have successfully mapped out topological phonons with meV-resolution, which is sufficient for detecting the nodal-chain phonons in K2O.

Currently, the study of topological nodal phonons is still at an early stage, mostly driven by academic interest. These phonons may have impacts on observable physical properties or effects. For example, as argued by Singh et al. 41, phonon band crossings tend to introduce phonon-phonon scattering centers, which suppresses the lattice thermal conductivity and may enhance the thermoelectric performance. As for the drumhead surface phonon modes, Zhang et al. 43 suggested that they may induce surface electronic structure anomalies through electron-phonon coupling. This may promote the possibility of surface superconductivity. In addition, most catalytic processes also occur on the surfaces. The topological surface phonon modes may in some cases promote the catalysis if the phonon frequency is in resonance with certain mid steps in the reaction. Certainly, these are still preliminary speculations. Possible applications of these topological phonons will require more future research works.

Note added. During the review of our work, a work by Tang and Wan appeared71, which did a systematic study of all band nodal structures in the 1651 magnetic space groups and 528 magnetic layer groups for both spinless and spinful systems. In the five-candidate space groups, their results are consistent with our analysis here.

Methods

Details of first-principles calculations

Density functional theory (DFT) calculations were conducted by using the Vienna ab initio simulation package (VASP)72,73. The projector augmented wave (PAW) pseudopotentials were adopted in the calculation74,75. Generalized gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof (PBE)76 realization was adopted for the exchange-correlation potential. The valence electrons treated in the calculations include K (3s23p64s1) and O (2s22p4). The kinetic energy cutoff was fixed to 520 eV. Γ-centered 10 × 10 × 10 k point mesh was adopted for the self-consistent calculations. The energy and force convergence criteria were set to be 10−7 eV and 0.001 eV Å−1, respectively. We used density functional perturbation theory (DFPT)77 in combination with the Phonopy package78 to obtain the force constants and phonon spectra. A supercell of 3 × 3 × 3 is adopted for the calculation of force constants. Nonanalytical correction (NAC) was considered in treating the long-range interaction of the macroscopic electric field induced by the polarization of the collective ionic motions near the Γ point, following the approach of ref. 79. For computing the surface phonon spectrum, we first calculated the second rank tensor of force constant in Cartesian coordinates from DFPT, from which we can get the tight-binding parameters for the bulk and surface atoms78. Then we obtain the surface Green’s function iteratively by using the WannierTools package80,81,82.