Abstract
Objects at finite temperature emit thermal radiation with an outward energy–momentum flow, which exerts an outward radiation pressure. At room temperature, a caesium atom scatters on average less than one of these blackbody radiation photons every 108 years. Thus, it is generally assumed that any scattering force exerted on atoms by such radiation is negligible. However, atoms also interact coherently with the thermal electromagnetic field. In this work, we measure an attractive force induced by blackbody radiation between a caesium atom and a heated, centimetre-sized cylinder, which is orders of magnitude stronger than the outward-directed radiation pressure. Using atom interferometry, we find that this force scales with the fourth power of the cylinder’s temperature. The force is in good agreement with that predicted from an a.c. Stark shift gradient of the atomic ground state in the thermal radiation field1. This observed force dominates over both gravity and radiation pressure, and does so for a large temperature range.
Similar content being viewed by others
Main
Quantum technology continues to turn formerly unmeasurable effects into technologically important physics. For example, minuscule shifts of atomic energy levels due to room-temperature blackbody radiation have become leading influences in atomic clocks at or beyond the 10−14 level of accuracy2. They have thus become important to precision timekeeping3, and for applications such as improving time standards, relativistic geodesy and searches for variations of fundamental constants. Thermal radiation from a heated source should also result in a repulsive radiation pressure on atoms through absorption of photons4,5,6,7. However, the scattering rate for room-temperature blackbody radiation is small, leading to only mm s−1 velocity changes in hundreds of thousands of years for the caesium D line, for example. Here, we show that spatially inhomogeneous blackbody radiation produces a much higher acceleration at the μm s−2 level pointing towards the source, even near room temperature. It is well described by the intensity gradient of blackbody radiation that gives rise to a spatially dependent a.c. Stark shift1, similar to the dipole forces induced by lasers in optical tweezers8, atom trapping9, or coherent manipulation of atoms10 or of molecular clusters11. We expect it to be the dominant force on polarizable objects over a large temperature range1 and thus important in atom interferometry, nanomechanics or optomechanics12. Controlling this force will enable higher precision in atom interferometers, including tests of fundamental physics such as of the equivalence principle13,14,15, planned searches for dark matter and dark energy16, gravity gradiometry17,18, inertial navigation and perhaps even Casimir force measurements and gravitational wave detection19,20.
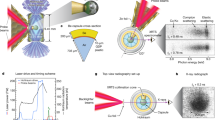
As shown in Fig. 1, we perform atom interferometry with caesium atoms21 in an optical cavity to measure the force induced by blackbody radiation. Our setup is similar to the one we used previously22,23. Caesium atoms act as matter waves in our experiment. They are laser-cooled to a temperature of about 300 nK and launched upwards into free fall, reaching 3.7 mm into the cylinder at their apex. During free fall, we manipulate them with counterpropagating laser beams, which “kick” the atoms with an impulse ℏkeff from two photons. The intensity and the duration of the laser pulses determine whether we transfer the atom with a 50% probability (a “π/2-pulse”) or nearly 100% (a “π-pulse”), respectively. We apply a π/2–π–π/2 pulse sequence, spaced by intervals of T = 65 ms, that splits, redirects and recombines the free-falling atomic wavefunction, forming a Mach–Zehnder atom interferometer. The matter waves propagate along the two interferometer arms while accumulating an acceleration phase difference Δϕ = k eff a tot T 2, where a tot is the total average acceleration experienced by the atom in the laboratory frame. For spatially varying accelerations, the phase shift is calculated by integrating the potential energy and taking the difference between the two paths. Since in our case, the separation between paths is negligible on the spatial scale of the potential variations, this amounts to integrating an acceleration profile a(z) over the atom’s trajectory in free fall z(t):
a, Space–time diagram of each atom’s trajectories in our Mach–Zehnder interferometer. b, The intensity gradient of blackbody radiation surrounding a heated, hollow cylinder causes a force on atoms. The cylinder is made from non-magnetic metal (tungsten) and measures 25.4 mm in height and diameter. The cavity light passes the cylinder through a 10 mm bore at its centre to perform interferometry. c, Theoretical calculation of the acceleration of caesium atoms due to blackbody radiation, a BBR, as a function of the distance z along the cylindrical axis. The vertical axis is taken from the centre of the source mass. The grey shaded area marks the region inside the hollow core of the cylinder. Discontinuities in the predicted acceleration stem from simplifying edge effects at the entrance to the hollow cylinder.
The probability of the atom exiting the interferometer in one of the outputs is given by P = cos2(Δϕ/2).
At the start of each experimental run, we heat the cylinder to a temperature of about 460 K with an infrared laser, which is subsequently switched off. We then measure the acceleration of the atoms during the cool-down period of up to 6 h, while we monitor the temperature with an infrared sensor. When the source mass has cooled to near room temperature, we reheat it to start another run. Because the cylinder has a 5 mm slit on the side, we can change its position between a location close to the interferometer and a remote one23 without interrupting the cavity mode. This allows us to separate forces induced by the source mass from other forces, in particular the million-fold larger one from Earth’s gravity. The near position exposes the atoms to blackbody radiation arising from the source, while the far position serves as a reference. We then investigate the temperature dependence of the acceleration difference.
Figure 2 shows this measured acceleration a cyl as a function of the source mass temperature T s with a comparison to theory. The red dotted line in Fig. 2 shows the predicted acceleration a cyl = a BBR + a grav from both the gravitational pull a grav and the blackbody interaction a BBR = C(T s 4 − T 0 4) of atoms with the source mass. Here, a grav = 66 nm s−2 is calculated, T 0 = 296 K is the measured ambient temperature and C = −4.3 × 10−5 ± 0.6 (μm s−2 K−4) is calculated from the albedo and geometry of the source (see the Methods section). The model leaves no free parameters.
Measured acceleration as a function of the source mass temperature T s. A quartic dependence on T s is observed for the acceleration experienced by caesium atoms towards the source mass. a, Data from 63 thermal cycles, about 2–5 h each, are binned in temperature with N bin = 65 measurements per bin. The black dots represent the weighted mean of each bin. Vertical error bars show the 1-sigma statistical uncertainty on the weighted mean. Systematic effects have been considered in detail and show no significant contributions to the error bars; see the Methods section. Horizontal bars show the temperature spread of the N bin measurements in the bin. The red dotted line presents a calculation of the average acceleration imparted to the atoms during interferometry. The error for this theoretical prediction is dominated by the approximately 10% uncertainty of the source mass emissivity. The gravitational pull of the cylinder gives the room-temperature offset of the acceleration, indicated by the black dotted line at a grav = −66 nm s−2. b, Residuals from the bulk acceleration data (cyan) to the zero-parameter theory model. c, A histogram of the bulk residuals is well described by a normal distribution. A Gaussian fit to the histogram (black dot–dashed curve) has mean compatible with zero within the standard error of 29 nm s−2.
It is important to rule out artifacts that could partially mimic a blackbody-induced acceleration. For example, spatially constant energy-level shifts induced by the blackbody radiation (rather than an a.c. Stark shift gradient, which produces a force) can be ruled out because they would be common to both interferometer arms, and thus cancel out (see the supplement). The pressure applied by hot background atoms from outgassing of the heated source mass removes a substantial fraction of the cold atoms from the detection region at its highest temperatures, so it is conceivably a component of the measured force on the remaining atoms. This, however, can be ruled out by multiple observations. First, this pressure should push the atoms away from the source, while the observed acceleration is towards the source. Second, it should depend exponentially on the source mass temperature; such an exponential component is not evident in the data. Finally, any scattering of hot background atoms with atoms that take part in the interferometer would be incoherent, and would reduce the visibility of our interference fringes. Figure 3, however, shows that the visibility is constant over our temperature range, ruling out scattering. This observation also confirms that absorption or stimulated emission of incoherent blackbody photons is negligible (see Fig. 4).
Visibility as a function of temperature, averaged in bins of 2 K for clarity. Scattering or absorption of photons would lead to a dephasing of the atomic ensemble, resulting in a reduction of visibility. No obvious loss of visibility is a strong indication that the contribution of scattering and absorption events is negligible. The inset shows interference fringes taken at T s = 437 K and T s = 326 K. Each fringe consists of 80 experimental runs with a cycle time of 1.2 s. The fitted fringe phase gives an acceleration measurement, contributing a data point to the bulk data seen in Fig. 2b,c.
The spectra of blackbody radiation for various temperatures compared with transition frequencies of ground-state caesium indicated by vertical lines. The dash–dotted line on the left refers to the hyperfine splitting of the ground state used in the current definition of the second. The dashed lines on the right are strong optical absorption lines of caesium, starting from the D1 transition 62S1/2 → 62P1/2 at 894 nm. The coloured band indicates the visible spectrum as a guide for the eye.
We now explain the measured acceleration in terms of a force due to the gradient in the ground-state energy-level shift (a.c. Stark effect) induced by blackbody radiation, h × 15 Hz at our highest temperatures, where h is the Planck constant. For the relevant temperature range, nearly all thermal radiation has a frequency well below the caesium D line. The shift of the atomic ground-state energy can be approximated by using the atom’s d.c. polarizability24 α Cs ≈ h × 0.099 Hz (V cm−1)−2 as2 ΔE(r) = −α Cs u(r)/(2ε 0), where u(r) is the electromagnetic energy density for the thermal field measured at a distance r from the source, and ε 0 is the vacuum permittivity. For isotropic blackbody radiation at the temperature T s of the source, we have u = 4σT 4/c (where c is the speed of light), and
where σ is the Stefan–Boltzmann constant. If the heated body is a sphere of radius R, then the sphere’s blackbody radiation will dilute with distance, with energy density u(r) proportional to R 2/(4r 2). Taking the gradient gives the acceleration from the blackbody radiation force1 in spherical geometry:
The force points radially inwards (except for atoms in an excited state, whose polarizability may be negative). To model the force in our experiment, we use analytical ray tracing to take the geometry of our setup into account (see the Methods section).
The force exerted on a polarizable object due to the intensity gradient of the blackbody radiation can be derived from the same fluctuation electrodynamic formalism as the temperature-dependent Casimir–Polder force25,26. Conventionally, thermal Casimir–Polder forces are considered in planar geometry, where the intensity gradient due to propagating radiation modes becomes zero, and only the contribution of evanescent fields remains. Such forces dominate at a length scale of the thermal wavelength λ T = hc/(k B T), and scale in different asymptotic regimes as the first or second power of the surface temperature26,27. In our experiment, the Casimir–Polder force is negligible due to the millimetre-scale distance between the atoms and the surface. However, the intensity of blackbody radiation of a finite-sized source body is spatially dependent, and the propagating-mode contribution must be taken into account1. This gives rise to a long-range force having the characteristic T 4 scaling of blackbody radiation, which we observe here for the first time.
Just as blackbody radiation affects atomic clocks2,3, the acceleration due to the blackbody field gradient observed here influences any high-precision acceleration measurements with polarizable matter, including atomic and molecular interferometers, experiments with nanospheres and potentially measurements of the Casimir effect and gravitational wave detectors. For example, inside a thin cylindrical vacuum chamber, the thermal radiation field nearly follows the local temperature T(z) of the walls, inducing an acceleration of atoms of
where m At and α At are the atom’s mass and static polarizability. Simulations confirm this approximation for thin cylinders, even for walls with per cent-level emissivity. For caesium atoms, for example, a linear temperature gradient of T′(z) = 0.1 K m−1 around a base of 300 K would result in a ≈ 10−11 m s−2, non-negligible in, for example, terrestrial and space-borne high-precision measurements including tests of the equivalence principle, gravity measurements and gradiometers or gravitational wave detection with atom interferometry. Effects will be suppressed in nearly overlapped simultaneous conjugate interferometers used for measuring the fine-structure constant28,29. The acceleration can be mitigated by monitoring and/or equalizing the temperature across the vacuum chamber, or (as shown by our simulations) by using wide, highly reflective vacuum chambers, wherein multiple reflections make the thermal radiation more isotropic. On the other hand, blackbody radiation can be used to simulate potentials. For example, heated test masses could be used to calibrate an atom interferometer for measuring the gravitational Aharonov–Bohm effect30.
Methods
Atom interferometer
Caesium atoms are magneto-optically trapped inside an ultrahigh-vacuum chamber, laser-cooled to a temperature of about 300 nK using Raman sideband cooling31 and prepared in the magnetically insensitive F = 3, m F = 0 hyperfine ground state. We use laser pulses enhanced by the optical cavity to manipulate the atomic wavepackets (Fig. 1a). An atom in the F = 3 state with momentum p 0 absorbs a photon with momentum +ℏk and is stimulated to emit a photon with momentum −ℏk. The atom emerges in the F = 4 state and at a momentum of p 0 + ℏkeff, where k eff = 2k. We can set the intensity and the duration of the laser pulses to transfer the atom with a 50% probability (a “π/2-pulse”) or nearly 100% (a “π-pulse”), respectively. A π/2–π–π/2 pulse sequence with pulses separated by a time T = 65 ms splits, redirects and recombines the free-falling atomic wavefunction, forming a Mach–Zehnder interferometer. Along the trajectory, the two interferometer arms accumulate an acceleration phase difference Δϕ = k eff a tot T 2, where a tot is the acceleration experienced by the atom in the laboratory frame. The probability of the atom exiting the interferometer in state F = 3 is given by P = cos2(Δϕ/2). Since the atoms are in free fall under the earth’s gravity, we chirp the laser frequencies in the laboratory frame at a rate of about 23 MHz s–1, so that the laser beams stay on resonance in the atoms’ frame of reference.
For efficient detection of the approximately 105 atoms at the interferometer output, we reverse the launch sequence to catch the sample. Non-participating atoms that have left the cavity mode due to thermal motion fall away. A pushing beam separates the state-labelled outputs of the interferometer. They are counted by fluorescence detection to determine P.
A single acceleration measurement is made by adjusting the rate of the gravity-compensation chirp to trace out oscillations of P with Δϕ. Fitting this fringe to a sine wave allows us to extract the phase, and thus the acceleration experienced by the atoms. Eight fringes are taken consecutively before toggling the source-mass position.
Test mass
The heated object is suspended inside the vacuum chamber by a non-magnetic (titanium) threaded rod (2.5 mm diameter) with a relatively low thermal conductivity of about 2 mW K−1. We heat the cylinder by shining a Nd:YAG fiber laser (IPG Photonics YLR-100-1064LP) through the slit into the bore, where it is better absorbed due to multiple reflections. Within 12 min at a laser power of 8 W, we heat the cylinder from room temperature to about 460 K.
Outgassing of the source mass
The background pressure varies with source mass temperature. Initially, outgassing of the cylinder at 460 K caused a pressure increase to about 10−7 mbar from a room-temperature vacuum of about 10−10 mbar (measured by an ion gauge about 50 cm away from the cylinder). After several heating cycles, this pressure increase was reduced to about 10−9 mbar.
Temperature measurement
The temperature is measured using an infrared temperature sensor (Omega OS150 USB2.2, spectral response 2.0–2.4 µm) through the vacuum chamber windows, which are made of fused silica and have a transmission cutoff just under λ ≈ 3 μm. The infrared sensor works across a temperature range of 320–440 K; outside this range, we can determine the temperature of the cylinder by extrapolation. This extrapolation is performed by calibrating the cooling curves to a heat-loss differential equation including both conduction and radiation.
Systematic effects
Possible artifacts that could influence this observation are well understood and can be ruled out, as follows.
Constant a.c. Stark shifts
In addition to the cancellation between interferometer arms mentioned in the main text, spatially constant a.c. Stark shifts would also be common to both ground-state hyperfine states, and thus cancel out even within each interferometer arm. This is because the blackbody radiation is very far detuned from any optical transition in the atom, and thus causes the same energy-level shift to both hyperfine ground states. To verify, we used the interferometer with opposite-sign wavevector ±k eff, implementing so-called “k-reversal“17. This inverts the signal k eff ⋅a tot T 2 arising from acceleration a tot but would not invert this constant a.c. Stark phase. We observe that the effect inverts sign with k eff, as expected for a force. Our results in Fig. 2 include data runs for both directions of the wavevector, performed independently, confirming a real acceleration.
Differential a.c. Stark shifts
The interferometer is asymmetric with respect to the apex of the trajectory, and therefore to the spatially varying differential a.c. Stark shift between the two interferometer arms. This spatial asymmetry leaves a residual differential a.c. Stark phase in the interferometer, which is largely suppressed by toggling the source-mass position. However, the source-mass position influences the radial distribution of the atom cloud, and since the small cavity beam waist (600 µm) is roughly the size of the cloud the spatial dependence of a.c. Stark shifts across the ensemble is exacerbated. By offsetting the Raman frequency pair with respect to cavity resonance (see our recent work23 for the full analysis), we tailor the a.c. Stark phases from pulses 1 and 3 to be equal and cancel within the interferometer. In our previous work, the interferometer with roughly the same asymmetry and shorter free-fall time T = 55 ms (now T = 65 ms) resulted in a measurement uncertainty of about 8 nm s−2. This is roughly two orders of magnitude smaller than the blackbody-induced acceleration a BBR.
Magnetic fields
The magnetic fields are identical to those in ref. 23. Phase shifts due to source-dependent magnetic fields give rise to an acceleration of only −2.5 ± 11 nm s−², less than 1% of the blackbody-induced acceleration.
Thermal expansion
Heating of the cylinder eventually transfers heat to the vacuum chamber, potentially causing thermal expansion. This could affect the interferometer by, for example, changing the cavity length. Such thermal expansion is avoided using a slow temperature feedback loop to hold the cavity distance constant throughout the experiment.
Surface effects
Near-field forces such as Casimir–Polder forces32 are suppressed, since the atoms never come closer to the source-mass surface than about 2 mm, and these forces decay at a length scale of the thermal wavelength, \({\lambda }_{{\rm{T}}}=hc/{k}_{{\rm{B}}}T\), λ T < 50 μm for T > 300 K.
Other effects
A more comprehensive analysis of systematic effects was carried out in ref. 23 using the same experimental setup. All effects analysed are found to be below the per cent level compared with the blackbody force.
Modelling
The inner surface of the cylinder was not accessible with the IR temperature sensor due to geometrical constraints. However, we assume similar emissivities due to similar surface finishes. The radiation experienced by the atom is the sum of the thermal fields from the source mass surface of temperature T s and the ambient radiation inside the vacuum chamber at temperature T 0. From the atom’s position z each of the i = 1, …, N radiating and reflecting surfaces covers a solid angle Ω i (z) such that the total shift of the ground-state energy level is given by
where J i denotes the radiant energy per unit area (radiosity) from the ith surface; for a black surface this is J i = σT i 4. For a diffuse grey body of emissivity 0 < ϵ i < 1, this changes to J i = ϵ i σT i 4 + (1 − ϵ i )G i , where G i is the radiation flux coming towards that surface, which is then reflected towards the atom.
For a more detailed calculation of the blackbody-induced acceleration, we model the tungsten cylinder as an opaque diffuse-grey surface whose absorptivity α and emissivity ϵ = α are independent of direction33 and whose reflectivity ρ = 1 − ϵ is constant over the considered temperature range. We have measured the cylinder’s emissivity at the bottom surface facing the atom as ϵ = 0.35 ± 0.05 by using an infrared temperature sensor. The radiation experienced by the atom is the sum of the thermal fields from the source-mass surface of temperature T s and the ambient radiation inside the vacuum chamber at temperature T 0. The outer surface of the cylinder reflects some of the ambient radiation such that J out = ϵσT s 4 + (1 − ϵ)σT 0 4. For the inner surface of the cylinder we account for internal reflection, which effectively increases the emissivity from that region33. The vacuum chamber itself is assumed large enough that we can ignore radiation originating from the cylinder and reflected by the walls of the vacuum chamber back to the atom. Finally, we also ignored that a segment has been cut out of the probe (see Fig. 1), and assume a radially symmetric hollow-core cylinder. Combining all these considerations, we can calculate the spatial dependence of the blackbody radiation intensity and therefore the level shift and the resulting forces on the caesium atoms as they approach the cylinder, as shown in Fig. 1. The jump in the acceleration at z = h/2 is a result of the sudden change in geometry seen by the atom as it enters the hollow cylinder. As the cylinder is cut open on one side this change will not be as pronounced for the actual setup.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Sonnleitner, M., Ritsch-Marte, M. & Ritsch, H. Attractive optical forces from blackbody radiation. Phys. Rev. Lett. 111, 23601 (2013).
Safronova, M. S. et al. Black-body radiation shifts and theoretical contributions to atomic clock research. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 57, 94–105 (2010).
Nicholson, T. L. et al. Systematic evaluation of an atomic clock at 2 × 10−18 total uncertainty. Nat. Commun. 6, 6896 (2015).
Nichols, E. & Hull, G. Pressure due to light and heat radiation. Astrophys. J. 15, 62 (1902).
Lebedev, P. N. & Lazarev, P. P. Die Druckkräfte des Lichtes, zwei Abhandlungen (Engelmann, 1913).
Burns, J. A., Lamy, P. L. & Soter, S. Radiation forces on small particles in the solar system. Icarus 40, 1–48 (1979).
Shestakova, L. I. Solar radiation pressure as a mechanism of acceleration of atoms and first ions with low ionization potentials. Sol. Syst. Res. 49, 139–145 (2015).
Ashkin, A. & Dziedzic, J. M. Optical trapping and manipulation of viruses and bacteria. Science 235, 1517–1520 (1987).
Phillips, W. D. Nobel Lecture: Laser cooling and trapping of neutral atoms. Rev. Mod. Phys. 70, 721–741 (1998).
Cronin, A. D., Schmiedmayer, J. & Pritchard, D. E. Optics and interferometry with atoms and molecules. Rev. Mod. Phys. 81, 1051–1129 (2009).
Hornberger, K., Gerlich, S., Haslinger, P., Nimmrichter, S. & Arndt, M. Colloquium: Quantum interference of clusters and molecules. Rev. Mod. Phys. 84, 157–173 (2012).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Dimopoulos, S., Graham, P., Hogan, J. & Kasevich, M. Testing general relativity with atom interferometry. Phys. Rev. Lett. 98, 111102 (2007).
Schlippert, D. et al. Ground tests of Einstein’s equivalence principle: from lab-based to 10-m atomic fountains. Preprint at https://arxiv.org/abs/1507.05820 (2015).
Tino, G. M. et al. Precision gravity tests with atom interferometry in space. Nucl. Phys. B Proc. Suppl. 243/244, 203–217 (2013).
Hamilton, P. et al. Atom-interferometry constraints on dark energy. Science 349, 849–851 (2015).
McGuirk, J. M., Foster, G. T., Fixler, J. B., Snadden, M. J. & Kasevich, M. A. Sensitive absolute-gravity gradiometry using atom interferometry. Phys. Rev. A 65, 33608 (2002).
Rosi, G., Sorrentino, F., Cacciapuoti, L., Prevedelli, M. & Tino, G. M. Precision measurement of the Newtonian gravitational constant using cold atoms. Nature 510, 518–521 (2014).
Canuel, B. et al. Exploring gravity with the MIGA large scale atom interferometer. Preprint at https://arxiv.org/pdf/1703.02490.pdf (2017).
Graham, P. W., Hogan, J. M., Kasevich, M. A. & Rajendran, S. New method for gravitational wave detection with atomic sensors. Phys. Rev. Lett. 110, 171102 (2013).
Peters, A., Chung, K. & Chu, S. Measurement of gravitational acceleration by dropping atoms. Nature 400, 849–852 (1999).
Hamilton, P. et al. Atom interferometry in an optical cavity. Phys. Rev. Lett. 114, 100405 (2015).
Jaffe, M. et al. Testing sub-gravitational forces on atoms from a miniature, in-vacuum source mass. Nat. Phys. 13, 938–942 (2017).
Micalizio, S., Godone, A., Calonico, D., Levi, F. & Lorini, L. Blackbody radiation shift of the Cs 133 hyperfine transition frequency. Phys. Rev. A 69, 53401 (2004).
Henkel, C., Joulain, K., Mulet, J.-P. & Greffet, J.-J. Radiation forces on small particles in thermal near fields. J. Opt. A Pure Appl. Opt. 4, 356 (2002).
Antezza, M., Pitaevskii, L. P. & Stringari, S. New asymptotic behavior of the surface-atom force out of thermal equilibrium. Phys. Rev. Lett. 95, 113202 (2005).
Obrecht, J. M. et al. Measurement of the temperature dependence of the Casimir–Polder force. Phys. Rev. Lett. 98, 063201 (2007).
Bouchendira, R., Cladé, P., Guellati-Khélifa, S., Nez, F. & Biraben, F. New determination of the fine structure constant and test of the quantum electrodynamics. Phys. Rev. Lett. 106, 80801 (2011).
Parker, R. H. et al. Controlling the multiport nature of Bragg diffraction in atom interferometry. Phys. Rev. A 94, 53618 (2016).
Hohensee, M., Estey, B., Hamilton, P., Zeilinger, A. & Müller, H. Force-free gravitational redshift: proposed gravitational Aharonov–Bohm experiment. Phys. Rev. Lett. 108, 230404 (2012).
Treutlein, P., Chung, K. Y. & Chu, S. High-brightness atom source for atomic fountains. Phys. Rev. A 63, 51401 (2001).
Scheel, S. & Buhmann, S. Y. Casimir–Polder forces on moving atoms. Phys. Rev. A 80, 42902 (2009).
Siegel, R., Howell, J. R. & Menguc, M. P. Thermal Radiation Heat Transfer 5th edn (CRC Press, 2010).
Acknowledgements
We thank Randy Putnam for collaboration in the laboratory and Dennis Rätzel for stimulating discussions. This material is based upon work supported by the David and Lucile Packard Foundation, the National Science Foundation under grant no 037166, the Defense Advanced Research Projects Agency grant no 033504, and the National Aeronautics and Space Administration grants nos 041060-002, 041542, 039088, 038706 and 036803. We also acknowledge collaboration with Honeywell Aerospace under DARPA contract no N66001-12-1-4232. O.S. was supported by HFSP fellowship LT000844/2016-C. M.S. was supported by the ERC Advanced Grant (247024 catchIT) and the Royal Society (RP150122). P.H. and M.S. thank the Austrian Science Fund (FWF): J3680, J3703.
Author information
Authors and Affiliations
Contributions
P.H., M.J., V.X., O.S. and H.M. designed the experiment, made the measurements and carried out the data analysis. M.S., M.R.M. and H.R. carried out numerical simulations of the blackbody force. All authors contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Haslinger, P., Jaffe, M., Xu, V. et al. Attractive force on atoms due to blackbody radiation. Nature Phys 14, 257–260 (2018). https://doi.org/10.1038/s41567-017-0004-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-017-0004-9
This article is cited by
-
Measuring gravitational attraction with a lattice atom interferometer
Nature (2024)
-
Exploring the foundations of the physical universe with space tests of the equivalence principle
Experimental Astronomy (2021)
-
A fibered laser system for the MIGA large scale atom interferometer
Scientific Reports (2020)
-
Optomechanical resonator-enhanced atom interferometry
Communications Physics (2020)