Abstract
Geometric arrays of vortices found in various systems owe their regular structure to mutual interactions within a confined system. In optics, such vortex crystals may form spontaneously within a resonator. Their crystallization is relevant in many areas of physics, although their usefulness is limited by the lack of control over their topology. On the other hand, programmable devices like spatial light modulators allow the design of nearly arbitrary vortex distributions but without any intrinsic evolution. By combining non-Hermitian optics with on-demand topological transformations enabled by metasurfaces, we report a solid-state laser that generates 10 × 10 vortex laser arrays with actively tunable topologies and non-local coupling dictated by the array’s topology. The vortex arrays exhibit sharp Bragg diffraction peaks, witnessing their coherence and topological charge purity, which we spatially resolve over the whole lattice by introducing a parallelized analysis technique. By structuring light at the source, we enable complex transformations that allow to arbitrarily partition orbital angular momentum within the cavity and to heal topological charge defects, thus realizing robust and versatile resonators for applications in topological optics.
Similar content being viewed by others
Main
In many natural systems, ensembles of vortices can self-organize into regular patterns through their mutual interaction1. This is the case for clusters of cyclones encircling the poles of Jupiter2, knotted lattices in chiral liquid crystals3 and motile haploid cells of sea urchins swimming in vortex trajectories4. In broad-area lasers, the crystal-like arrangements of optical vortices can also form spontaneously due to the nonlinear interaction of several competing transverse modes5,6. These crystals consist of arrays of intensity nulls, each corresponding to a phase singularity of the field carrying orbital angular momentum (OAM) with a topological charge7,8. The self-organizing nature of these vortex crystal lasers solves a difficult energy minimization problem, making them relevant in many areas of physics. Although fascinating as a nonlinear dynamic system, these optical vortex crystals are unsuitable for practical applications in topological optics, as the laser states can be non-stationary9 and their topology cannot be tuned at will. Thus, the applications requiring vortex arrays10,11, including parallelized super-resolution imaging12, OAM-multiplexed communications13 and multiparticle micromanipulation with optical tweezers14,15, have turned their attention to alternative generation schemes, ranging from spatial light modulators (SLMs) and Dammam gratings16 to metamaterials17,18,19,20,21. However, all these extracavity implementations carve out the vortices from an input beam profile, resulting in reduced efficiency. Moreover, these devices only realize the photonic design programmed by the user without exhibiting an internal evolution, thus losing the appeal of an active system. A recent approach is to coherently combine multiple microring lasers based on supersymmetry, which is promising for power scaling but is currently limited to a topological charge of one22.
In this work, we present a structured light laser23 capable of producing vortex laser arrays with a topology that is directly tailored at the source. Just as in a broad-area laser, our gain medium has a large transverse cross-section supporting many transverse modes. Instead of allowing these modes to structurally self-organize in the resonator, we force them to form a lattice of a hundred laser beams by inserting a mask that modulates the phase and amplitude of the field24,25. The phase profile is designed to impart arbitrary OAM values to each beam of the lattice; consequently, we artificially introduce an amount of OAM in the system that must be conserved. This effectively partitions the resonator into two sections—one on either side of the OAM-transforming mask— each emitting a laser array imbued with a different topological charge. We spatially couple the vortices using a non-Hermitian mechanism that introduces dissipative losses in the resonator, making the system stable and coherent, and resulting in a ‘crystallization’ of the array phase. The coupling network is not limited to the nearest neighbours as for arrays of Gaussian lasers with no topological charge, but instead can be tailored to mix vortices that are widely separated in the lattice. Although different schemes for generating a single vortex inside a resonator have been demonstrated19,26,27,28,29,30, this work accomplishes the conditions for generating vortex laser arrays in a single cavity, realizing a platform to explore complex topological transformations and collective vortex effects at the source.
Results
Operating principle of the metasurface laser
The resonator comprises a diode-pumped neodymium-doped yttrium aluminium garnet (Nd:YAG) laser with a high Fresnel number in a self-imaging (4f) configuration (Fig. 1a), supporting a very large number of transverse modes (~105) (ref. 31). Two intracavity lenses, which form a telescope system, image the plane of the metasurface array onto the opposite end of the cavity, where an output coupler (OC) is present (Materials). The other OC is displaced from the metasurface array to couple the laser beams via the Talbot effect. The metasurface array provides the necessary intracavity topological charge conversion. It consists of 10 × 10 metasurfaces in a square-lattice geometry with amorphous Si nanopillars on a fused SiO2 substrate (Fig. 1b). Different vortex-plate designs are possible, either based on the Pancharatnam–Berry phase (such as q plates32,33 that are used in this work) or on the propagation phase such as (J plates34; Supplementary Information). The general requirement is that the circulating beam does not acquire any net topological charge on a double pass through the metasurface array. This condition cannot be satisfied using a polarization-independent spiral phase plate in a plane-parallel resonator35, but we achieve this by exploiting the engineered birefringence of a metasurface, in combination with the appropriate intracavity polarization optics, for complete spin–orbit control of the beam (Supplementary Information provides details on how the round-trip condition is satisfied). The spin–orbit conversion is provided by the geometric phase elements of the metasurfaces, which convert circularly polarized light carrying spin angular momentum (SAM) into a beam with opposite handedness and an OAM quantity dictated by the spatial orientation of the nanopillars34.
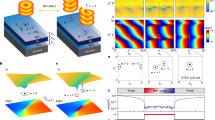
a, Schematic of the cavity containing a metasurface array (MA) with charge ℓa dividing the resonator into two sections with different topological charges, namely, 0 and ℓa. A 4f telescope (with two lenses) images the MA onto the left OC. A pinhole forces the beams to carry zero topological charge in the telescope section. The vortex array is coupled by diffraction and forms a self-image after a round-trip distance of zT/2 due to the Talbot effect. The polarization optics exploit the metasurface birefringence to convert the beam’s spin–orbit state (α and β). b, Optical image of the MA (ℓa = 1). The top inset shows a scanning electron microscopy image of the engineered nanopillars. c, Experimental NF and FF sharp intensity distributions of the arrays emitted from opposite ends of the cavity. d, Simulated Talbot carpet of an out-of-phase vortex array propagating along the z direction. e, Convolution theorem applied to a vortex array explaining its FF pattern. \({{{\mathcal{F}}}}\), Fourier transform. Scale bars are 300 μm, except for the scanning electron microscopy scale bar (500 nm).
The telescope configuration gives direct experimental access to the far-field (FF) plane, which is physically located between the two intracavity lenses and contains the optical Fourier transform (FT) of the near field (NF) of the metasurface array. By placing a pinhole in the FF, it is possible to filter high-spatial frequency components of the beam without reducing the gain effective area or affecting the laser efficiency31,36,37. Since the metasurface array separates the cavity into two sections with different topological charges, an FF pinhole allows us to force the existence of the Gaussian beams—having the smallest spatial frequency content in the FF—on the telescope segment of the cavity, leaving the vortex beams in the Talbot section.
The interstices between the metasurfaces of the array are filled with a metallic mask that spatially filters the beams’ transmission. The beams diffract at every metasurface aperture, resulting in an array of interfering vortices (Supplementary Videos 1 and 2). Due to the periodic arrangement of the vortices, the Talbot effect ensures that self-images of the array are created at specific planes along the propagation direction (Fig. 1d, Talbot carpet), whose positions, in general, depend on the phase relation among the vortices. At the characteristic Talbot distance zT = 2d2/λ of a square array, where d = 0.3 mm is the period and λ = 1,064 nm is the laser wavelength, an array of both in-phase and out-of-phase vortices—where the nearest neighbours have a phase difference of 0 and π, respectively—will form a self-image37. This degeneracy of the phase solutions is lifted at zT/2, where only an out-of-phase array can produce a self-image; therefore, we use this distance in our system. Since the Talbot propagation path is folded in the resonator, this requires us to set a distance of zT/4 = 42 mm between the metasurface array and the nearest OC (Fig. 1a). The amplitude mask combined with Talbot propagation allows to select the lowest-loss phase solution for the array over several round trips. Since the lasers of the array operate at several frequencies corresponding to different longitudinal modes of the cavity, a phase-locking mechanism is needed to synchronize them24. In our cavity, the linear coupling together with the saturable nonlinearity of the gain medium provide mode competition and favour the minimal-loss solution (Supplementary Fig. 13).
The generation of a vortex laser array is demonstrated in Fig. 1c. Different NF intensity distributions are observed at each end of the cavity: one corresponding to an array of Gaussian beams and the other to an array of donut beams with dark cores, signalling the occurrence of a topological charge conversion inside the cavity. The phase coherence of the arrays is witnessed by the Bragg diffraction peaks present in the FF distribution, obtained by the FT of the NF distributions. The Bragg pattern of the vortex array can be easily understood using the convolution theorem. Since a vortex array corresponds to the convolution of a Dirac comb with a vortex beam (Fig. 1e, first column), its FT is simply given by the point-wise product of the FTs of the Dirac comb and the vortex, resulting in a single, large pixelated vortex (Fig. 1e, second column). The experimental results are in very good agreement with the numerical Fox–Li simulations of the laser, which include the saturable gain nonlinearity, proving that the measured lasing mode is the one experiencing the lowest loss in the cavity (Supplementary Fig. 6 and Methods).
Parallelized topological charge analysis
The Bragg diffraction peaks are a signature of phase locking in the vortex laser array, but they do not directly show the value of the topological charge carried by the vortices. A standard approach to analyse the topological charge of a vortex is to perform a modal decomposition by measuring the inner product between the field and appropriate correlation filters. In general, a single beam could be selected by applying a digital aperture on an SLM in the NF of the array and its charge revealed by displaying a phase and amplitude hologram of the opposite charge, leading to an intensity peak at the beam’s optical axis in the FF38. However, this is an inefficient technique for an array, with a long sequential processing time proportional to the number of vortices. By exploiting the fact that each vortex in the array is imaged to the same FF profile regardless of its position in the array (Fig. 2a) and by using the linearity of the FT, we introduce a parallelized technique to analyse the topological charge of each beam in the array all at once. Using an SLM, we carry out a modal decomposition of all the vortices in the FF and measure their respective on-axis intensity in the NF (Materials). The modulated beams will now have a charge given by the sum of the decomposition charge displayed on the SLM and the intrinsic one of the array. This corresponds to a lattice of Gaussians when the SLM and array charges have equal values but opposite signs, and to an array of donuts of variable radii in all the other cases (Fig. 2f). In Fig. 2b–e, we present the results for a metasurface array with charge ℓa = 1. The measured charge purity statistically averaged over the array is near 100% for right- and left-circularly polarized light. We also note that the total summed OAM of the beam is conserved in the NF-to-FF propagation: in the NF, we have 100 beamlets separated in space, each with a charge of ℓa, whereas in the FF, we have 100 superimposed beams—still with a charge of ℓa—that interfere and produce a pixelated donut beam. By changing the intracavity polarization optics, it is also possible to generate vector vortex arrays with azimuthally and radially polarized light, corresponding to a superposition of opposite charges (ℓ = ±1; Fig. 2d,e). In this case, a small contribution at ℓ = 0 is also present (4%) due to a residue of the beam that is not converted by the metasurface array and not filtered outside the cavity (Supplementary Information). In the rest of this work, we will concentrate on scalar vortex beams, keeping the focus on the topological optics aspects of the laser.
a, Each vortex in the array is projected to the same location in the FF plane using a lens. In the FF, a hologram encoded to modulate both phase and amplitude is displayed on an SLM to carry out the charge analysis. A second lens re-images the entire array in the NF, where the new beam profiles carry information about the charge of the input vortices. The SLM operates in reflection with a first-order diffraction grating, but here it is shown in transmission and at zero order for simplicity. b–e, Topological charge spectra statistically averaged over the whole array for a metasurface array with a charge of one integrated in the laser. The different cases correspond to left-circular (b), right-circular (c), radial (d) and azimuthal (e) polarization outputs. The dots indicate the mean and the error bars indicate the standard deviation of the values in the vortex array. f, Topological charge decomposition of each vortex in the array for the laser with left-circular polarization (top). Images of the modulated array obtained with different SLM holograms are also shown (bottom).
Scaling up the topological charge
Our metasurface laser scheme allows to scale up the charge of the vortex array by increasing the azimuthal gradient in the phase design of the metasurfaces. We characterized an array with a charge of 5 (Supplementary Fig. 7). Due to a charge-dependent increase in the vortex core, the typical diameter of the donuts observed in the NF is 150 ± 10 μm (Fig. 3a), larger than that of the charge-1 donuts shown above with 91 ± 5 μm (Fig. 1c)—a size change in agreement with the numerical simulations (138 ± 8 and 90 ± 9 μm, respectively). The larger topological charge content of each laser in the vortex array is also manifested in the FF distribution (Fig. 3a), corresponding again to a pixelated vortex but with a dark core larger than the charge-1 case.
a, Experimental NF and FF distributions of a vortex array with ℓ = 5, showing large dark cores. All the scale bars are 300 μm. b, Topological charge spectrum of the vortices. The dots indicate the mean, and the error bars indicate the standard deviation of the values in the vortex array. c, Magnitude of the coupling coefficient ∣κi,j∣ calculated between each vortex in the array (indexed by j, with j varying over all the array positions) and the one located at the centre (indexed by i). The size of the coupling network increases with ℓ. The dominant contributions in the ℓ = 5 case are marked by arrows. In all the plots, the grids define the positions of the array.
The topological charge purity remains high, with a peak at ℓ = 5 around 90% (Fig. 3b). The small spurious contributions at the other charges are due to imperfect Talbot reconstruction in the peripheral regions of the array. This can be understood by examining the coupling network of the array, which is more complicated than for arrays without topological charge, where coupling is dominated by the nearest neighbours (ℓ = 0; Fig. 3c). The coupling matrix κi,j of the vortex array is non-Hermitian39,40, being complex, with an imaginary component due to transmission losses at the mask, and symmetric, like the field propagation from one vortex to another; thus, \({\kappa }_{i,j}^{* }\ne {\kappa }_{j,i}={\kappa }_{i,j}\). We calculate the magnitude of κi,j for any position j in the array and i corresponding to a central position37. This quantity is normalized to the self-coupling, which is the amount of energy that laser i transfers back to itself. Considering a vortex array with ℓ = 5 (Fig. 3c), the coupling is strong, as the main energy comes from relatively distant vortices lying on a large circle. On the other hand, the self-coupling tends to zero due to the intensity null of the vortex that—after expansion in a Talbot round trip—transfers negligible energy to the initial site. When i corresponds to the position of a vortex far from the centre of the array, the power coupling will be anisotropic due to the finite size of the array, forming a vortex with an asymmetric donut intensity profile and fractional OAM producing small sidebands in the topological charge spectrum. These effects are less pronounced for small charges (Fig. 3c; ℓ = 1) and can be mitigated by increasing the array size.
Partitioning OAM inside the cavity
The spin–orbit transformations implemented in our cavity, in principle, allow for several topological solutions, each comprising a pair of vortex arrays with different topological charges occupying the two sides of the metasurface array. We denote a generic topological solution as (m∣n), where m and n are the charges of the arrays on the telescope and Talbot segments of the cavity, respectively. OAM conservation imposes the condition m + ℓa = n, where ℓa is the metasurface array charge. Until here, the use of the FF pinhole forced the appearance of beams with zero charge in the telescope section, imposing the solution (0∣ℓa).
After removing the FF pinhole, there could be many degenerate solutions. However, this degeneracy is lifted by two main elements in the cavity, giving topological charge-dependent losses and favouring a specific solution. Both types of loss are dissipative and originate from the spatial filtering of the mask, after the beam has made a round trip in each segment of the cavity (Fig. 4a). The first contribution relates to a round trip in the telescope section. We find that a small deviation Δz in cavity length from the ideal 4f value produces a topological charge-dependent transmission efficiency through the mask, due to the divergence of the beams (Fig. 4c). The second contribution is connected with a round trip in the Talbot section. Due to the finite size of the array, part of the Talbot self-image does not overlap with the original array but rather spills out around its edges41, getting blocked by the mask. Since the spillover increases with the divergence of the diffracting beams, the transmission efficiency diminishes with the charge (Fig. 4d). The two described effects are in competition and the lowest-loss solution chosen by the laser depends on Δz.
a, Partitioning of OAM in the cavity originates from the spatial filtering of the mask following a round trip in either the telescope or Talbot section of the cavity, whose loss is charge dependent. The first telescope loss depends on cavity adjustment Δz with respect to the 4f value. Experimental images of the representative beams extracted from two arrays emitted from the same side of the laser (array charge ℓa = 1) for different Δz/4f values are also shown, together with the array charge spectra. The dots indicate the mean and the error bars indicate the standard deviation of the values in the vortex array. b, Regions of existence of the various topological solutions as a function of the metasurface array charge and Δz/4f. The solutions are written as (m∣n), where m and n are the charges of the arrays on the telescope and Talbot section of the cavity, respectively. c,d, Calculated transmission efficiency (ηtelescope (c) and ηTalbot (d)) of a 10 × 10 array of vortex beams filtered by the mask after a round trip through the telescope and Talbot sections. e, Combination (ηtot) of the two calculated topological charge-dependent losses determines which topological solution is favoured by the laser as a function of Δz, corresponding to the curve with the largest transmission. The case of ℓa = 1 is shown.
By combining the telescope and Talbot efficiencies, we calculate the total transmission efficiency for a full round trip in the resonator. As shown in Fig. 4e, in the case of ℓa = 1, there are two possible topological solutions, namely, (0∣1) and (−1∣0), dominating in different ranges of the tuning parameter with a transition point around Δz/4f = 0.8%. We experimentally verify the existence of these two solutions by displacing the OC on the telescope side by a few millimetres and measuring the change in topological charge spectrum of the array emitted from the Talbot side of the laser (Fig. 4a). Remarkably, the beams are donut shaped even when they do not carry any charge. This feature arises from the phase-only transformations operated by the metasurfaces, which unwind the phase but leave an amplitude term in the NF of the beams, as also observed in the laser simulations (Supplementary Information). These findings can be generalized for higher array charges, resulting in a set of ℓa + 1 different topological solutions, ranging from (0∣ℓa) to (−ℓa∣0) (Fig. 4b).
Healing of defects
So far, we have presented vortex laser arrays with topological charges determined by arrays of identical metasurfaces. Next, we break the symmetry of the array by introducing an intentional topological charge defect and study the properties of the resulting vortex array. We fabricate a 10 × 10 array with metasurfaces carrying a charge ℓa = 1, except for a defect device with charge ℓd = 2 located in the central region of the array (Fig. 5a). We remove the FF pinhole from the cavity and tune its length to sustain the (0∣ℓa) solution. At the output of the metasurface laser, we observe a vortex array with donut beams of the same size (Fig. 5b), as in the defect-free laser (Fig. 1c). Further examination of the spatially resolved topological charge spectrum reveals that in correspondence to the defect metasurface, the dominant component is ℓ = 1, as for the rest of the array, indicating the ability of the metasurface laser to heal the topological charge defect (Fig. 5c).
a, Optical microscopy image of a metasurface array with charge ℓa = 1 everywhere, except for an intentional defect with charge ℓd = 2 (encircled device). b, A vortex array emitted from the metasurface laser showing an array of donuts with similar size. All the scale bars are 300 μm. c, Topological charge spectra measured at the defect position (right) and over the rest of the array (left), demonstrating the healing of the charge defect. In the left plot, the dots indicate the mean and the error bars show the standard deviation of the values in the vortex array, excluding the value of the vortex at the defect position. d, Topological charge evolution in a cavity round trip for a double pass through the defect device (bottom) or any other metasurface in the array (top). e, Simulated defect healing efficiency, defined as the fraction of beam power at the defect location carrying a charge equal to that of the vortex array. The efficiency is shown as a function of the charge difference between the defect and array, Δℓ = ℓd − ℓa, where ℓa = 1 as in the experiment.
The defect recovery engine built into our laser is based on the topological version of the Talbot self-healing effect42: multiple passes through the Talbot section of the cavity remove non-periodic topological faults in the array, only strengthening the periodic components at the self-imaging plane. Following a full round trip through the cavity, we can see how the topological charge is repeatedly converted at the defect metasurface, resulting in a self-consistent solution (Fig. 5d; for the defect healing transient, see Supplementary Video 3). The additional charge introduced by the defect device does not disappear from the system, but, instead, it manifests itself in the telescope section as a beam with a new charge ±(ℓa − ℓd). As long as this beam can propagate through the telescope segment, any value of the topological charge of the defect will be recovered in the vortex array with high efficiency (Fig. 5e). Since this beam carries a charge larger than the surrounding array of the Gaussian beams (that is, in our experiment, ∣ℓa − ℓd∣ = 1 > 0), it suffers more losses by self-imaging in the telescope (Fig. 4c at Δz/4f = 1%), resulting in a donut with lower intensity than its neighbours (Fig. 5b). The fact that in our non-Hermitian system39,43, the presence of the defect increases the losses in the cavity, resulting in a change in the gain condition, is in sharp contrast with topological insulator lasers44, which are also robust to defects but feature a gain that is not affected by their presence owing to topological protection—a concept that does not easily lend itself to solid-state lasers. Finally, we note that multiple defects can be healed in the laser, provided that each defect is surrounded by a suitable neighbourhood as determined by the vortex coupling network (Fig. 3c). Supporting numerical studies investigating the dependence of self-healing on different properties of the system, such as coupling, defect location, charge and density, are described in the Supplementary Information.
Discussion
We have demonstrated a metasurface laser capable of controlling topological transformations in optical vortex arrays based on arbitrary spin–orbit conversions. The underlying non-Hermitian mechanism provides stability and coherence to the system, as well as the ability to partition OAM within the cavity. The concepts presented in this work open up several new possibilities. The spatial coupling geometry of a laser array could be engineered by judiciously tailoring the topological charge of the beams. Anisotropic configurations could also be realized by employing arrays with fractional OAM. This could serve to individually control mutually coupled channels in a network of communicating nodes. We have focused here on the steady-state generation of optical vortex laser arrays, but in the future, their charge can be dynamically modulated by adjusting the cavity length, either mechanically or optically. By combining the two laser arrays emitted from the opposite sides of the cavity, one can utilize the interference of the vortex array with the complementary zero-topological-charge Gaussian array to generate topologically protected lattices known as skyrmions45, endowed with the tuneable feature of our system. By exploiting the design freedom allowed by metasurfaces, many other topological coupling schemes can be explored, such as non-reciprocal OAM conversions, where the imparted charge depends on which side of the metasurface is seen by the beam propagating through the cavity. The healing of defects more generally shows that the system can respond and adapt to aperiodic features of the phase mask. This opens up the possibility of iteratively manipulating information encoded as topological charges and could be used to develop photonic simulators46 using OAM as a synthetic dimension, including an optical simulator of synthetic gauge fields47, and implementing quantum search algorithms in a laser solver with a marked array48. For instance, our laser arrays could be used to model the population dynamics of other physical systems, such as interacting galaxies or hydrodynamic vortices, mapping their angular momenta to different topological charges of the laser. In particular, it will be interesting to explore what happens when the system is tuned away from the regime of strong coupling and whether distinct domains of different topological charges can form in the laser array. Finally, our scheme is scalable and allows for the generation of large optical vortex arrays that could exploit spatial-division multiplexing49 for optical communications using multidimensional structured light50 with OAM, frequency and polarization degrees of freedom.
Methods
Metasurface arrays
The metasurfaces consist of 600-nm-tall Si nanopillars arranged on a hexagonal close-packed lattice and lying on a 500-μm-thick fused SiO2 substrate. The phase library of nanopillars was simulated for the Nd:YAG laser wavelength of 1,064 nm using a finite-difference time-domain software (Lumerical) and a complex-value refractive index measured by ellipsometry. Each metasurface has a diameter of 200 μm and is arranged in a 10 × 10 square array with 300 μm period. For these array parameters, the Talbot distance is zT = 169 mm. The metasurfaces employ either geometric or propagation phase to impart a topological charge to the beam. The interstices between the metasurfaces are filled with a thin Au layer, which serves as an amplitude mask. The fabrication of the metasurface arrays includes the following main steps. A 600-nm-thick Si film was deposited onto the fused SiO2 substrates by plasma-enhanced chemical vapour deposition (STS LPX PECVD system). Before electron-beam exposure, a 10-nm-thick Au film was deposited on top of the poly(methyl methacrylate) layer by physical vapour deposition, thus ensuring that there were no charging effects. Electron-beam direct writing of the metasurface arrays was carried out using an ultrahigh-resolution Raith150 Two electron-beam lithography system. During exposure, a beam energy of 20 keV was employed, setting the beam current to 140 pA. The Cr metasurface pattern obtained through lift-off was transferred to the Si film by means of a plasma-enhanced reactive ion etching system (Sentech SI500). The etched depth and sidewalls verticality were optimized by carefully tuning the process parameters (radio-frequency power, 18 W; pressure, 0.32 Pa; inductively coupled plasma power, 200 W; C4F8, 32 s.c.c.m.; SF6, 30 s.c.c.m.; Ar, 10 s.c.c.m.; temperature, 0 °C). The amplitude mask was finally realized using standard ultraviolet lithography (Süss MicroTec MA6/BA6 mask aligner system) and chemical etching.
Metasurface laser
The active medium of the laser is an Nd:YAG module with 40 laser diode bars (Cutting Edge Optronics, Northrop Grumman). The Nd:YAG rod is low doped (<1%), 146 mm long and 7 mm in diameter. The module is water cooled at 26 °C, and operated in the quasi-continuous-wave mode with 250 μs current pulses at 1 Hz repetition rate to avoid thermal lensing effects25. Different intracavity optics schemes can be employed depending on the type of phase used in the metasurface design. We first align the resonator using a simple array of apertures (not generating a vortex array), and then we replace this by the array of metasurfaces. The intracavity lenses forming the telescope have an anti-reflection coating designed for the lasing wavelength, and a focal length of 150 mm. The OCs have a reflectance above 97% (EKSMA Optics). The FF pinhole spatially filters the Fourier spectrum of the Gaussians, making their intensity distribution more uniform and improving the quality of the vortices generated from the metasurface. At the same time, the pinhole also blocks possible reflections from the metallic mask of the metasurface array. The FF pinhole can be removed if a non-reflective (non-metallic) amplitude mask is employed or when using J-plate metasurfaces in the vector-vortex-beam cavity configuration.
Numerical simulations
We carry out numerical simulations of the metasurface laser cavity based on the iterative Fox–Li method51, including the nonlinearity of the active medium via a gain matrix37. We start every simulation from a numerical noise seed to generate the initial complex field, which is then run through the cavity using the Fourier beam propagation method with an absorbing boundary layer52. In particular, the propagation through the telescope section is not realized by means of FTs converting the beam from the NF to the FF and vice versa; we rather implement phase matrices for the lenses and propagate the beam over the actual distances corresponding to our experimental setup. This allows calculating FF patterns in scale with the experimental ones, as well as to account for the finite aperture of the intracavity optical elements. Topological charge transformations are accounted for by implementing two different phase profiles on the opposite sides of the metasurface array, as those seen by the propagating beam.
Topological charge analysis
The setup for parallelized topological charge analysis consists of a 4f telescope with a phase-only SLM (HOLOEYE GAEA-2) lying at the Fourier plane in the middle of the two lenses. The SLM operates at the first diffraction order in the reflection mode, although in Fig. 2a, it is shown in the transmission mode for simplicity. As an initial charge analysis, we decompose the beam using a pitchfork hologram, corresponding to the interference of a spiral phase with a diffraction grating (for the operation at the first order). However, to correctly extract the relative weights among the different components of the topological spectrum, complex amplitude modulation is needed38. This translates into an additional phase mask showing up as an annular element in the SLM holograms. To define the hologram used in the complex amplitude modulation, we first fit the radius of the vortices imaged in the NF of the metasurface array and extract the corresponding beam waist ω0 of the embedded Gaussian53. Then, we simulate a single donut with the measured ω0 and the charge deduced from the pitchfork analysis, propagate it to the FF and extract the waist of the corresponding FF beam, which is used to program the SLM hologram. As the SLM only modulates horizontally polarized light, the circularly polarized light of the vortex laser array generated from q-plate arrays is converted into horizontally polarized light using a combination of quarter- and half-waveplates (not shown in Fig. 2a). A pinhole is used to block unwanted diffraction orders before the camera (Spiricon LT665) acquisition. The modal decomposition of the array is carried out over a basis of Laguerre–Gaussian modes with topological charge ranging from −2ℓ to 2ℓ, where ℓ is the array charge and p = 0 radial mode. The optical axis of the setup was aligned by sending an array of Gaussian beams generated using a calibration mask of apertures instead of the metasurface array. The modal decomposition and normalization of the topological charge spectra was carried out according to the method described elsewhere38. For each individual beam, the topological charge spectrum was extracted by measuring the intensity at their optical axis for every detection mode and then normalized by their sum. We employed background subtraction to remove noise from the acquired intensity images and set a noise threshold to exclude contributions of vortices that are too weak (<2%) from the statistical average of the array.
Data availability
All the relevant data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Jin, D. Z. & Dubin, D. H. E. Characteristics of two-dimensional turbulence that self-organizes into vortex crystals. Phys. Rev. Lett. 84, 1443–1446 (2000).
Adriani, A. et al. Clusters of cyclones encircling Jupiter’s poles. Nature 555, 216–219 (2018).
Tai, J.-S. B. & Smalyukh, I. I. Three-dimensional crystals of adaptive knots. Science 365, 1449–1453 (2019).
Riedel, I. H., Kruse, K. & Howard, J. A self-organized vortex array of hydrodynamically entrained sperm cells. Science 309, 300–303 (2005).
Brambilla, M. et al. Transverse laser patterns. I. Phase singularity crystals. Phys. Rev. A 43, 5090–5113 (1991).
Scheuer, J. & Orenstein, M. Optical vortices crystals: spontaneous generation in nonlinear semiconductor microcavities. Science 285, 230–233 (1999).
Coullet, P., Gil, L. & Rocca, F. Optical vortices. Opt. Commun. 73, 403–408 (1989).
Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, 8185–8189 (1992).
Staliunas, K. & Sanchez-Morcillo, V. J. Transverse Patterns in Nonlinear Optical Resonators (Springer, 2003).
Wang, X. et al. Recent advances on optical vortex generation. Nanophotonics 7, 1533–1556 (2018).
Shen, Y. et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 8, 90 (2019).
Vicidomini, G., Bianchini, P. & Diaspro, A. STED super-resolved microscopy. Nat. Methods 15, 173–182 (2018).
Ren, H., Li, X., Zhang, Q. & Gu, M. On-chip noninterference angular momentum multiplexing of broadband light. Science 352, 805–809 (2016).
Padgett, M. & Bowman, R. Tweezers with a twist. Nat. Photon. 5, 343–348 (2011).
Woerdemann, M., Alpmann, C., Esseling, M. & Denz, C. Advanced optical trapping by complex beam shaping. Laser Photonics Rev. 7, 839–854 (2013).
Lei, T. et al. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci. Appl. 4, e257 (2015).
Kildishev, A. V., Boltasseva, A. & Shalaev, V. M. Planar photonics with metasurfaces. Science 339, 1232009 (2013).
Yu, N. & Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 13, 139–150 (2014).
Maguid, E. et al. Topologically controlled intracavity laser modes based on Pancharatnam-Berry phase. ACS Photonics 5, 1817–1821 (2018).
Jin, J. et al. Multi-channel vortex beam generation by simultaneous amplitude and phase modulation with two-dimensional metamaterial. Adv. Mater. Technol. 2, 1600201 (2017).
Piccardo, M. & Ambrosio, A. Recent twists in twisted light: a perspective on optical vortices from dielectric metasurfaces. Appl. Phys. Lett. 117, 140501 (2020).
Qiao, X. et al. Higher-dimensional supersymmetric microlaser arrays. Science 372, 403–408 (2021).
Forbes, A. Structured light from lasers. Laser Photonics Rev. 13, 1900140 (2019).
Nixon, M., Ronen, E., Friesem, A. A. & Davidson, N. Observing geometric frustration with thousands of coupled lasers. Phys. Rev. Lett. 110, 184102 (2013).
Pal, V., Tradonsky, C., Chriki, R., Friesem, A. A. & Davidson, N. Observing dissipative topological defects with coupled lasers. Phys. Rev. Lett. 119, 013902 (2017).
Naidoo, D. et al. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat. Photon. 10, 327–332 (2016).
Sroor, H. et al. High-purity orbital angular momentum states from a visible metasurface laser. Nat. Photon. 14, 498–503 (2020).
Ito, A., Kozawa, Y. & Sato, S. Generation of hollow scalar and vector beams using a spot-defect mirror. J. Opt. Soc. Am. A 27, 2072–2077 (2010).
Cai, X. et al. Integrated compact optical vortex beam emitters. Science 338, 363–366 (2012).
Huang, C. et al. Ultrafast control of vortex microlasers. Science 367, 1018–1021 (2020).
Cao, H., Chriki, R., Bittner, S., Friesem, A. A. & Davidson, N. Complex lasers with controllable coherence. Nat. Rev. Phys. 1, 156–168 (2019).
Marrucci, L., Manzo, C. & Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 96, 163905 (2006).
Devlin, R. C. et al. Spin-to-orbital angular momentum conversion in dielectric metasurfaces. Opt. Express 25, 377–393 (2017).
Devlin, R. C., Ambrosio, A., Rubin, N. A., Mueller, J. P. B. & Capasso, F. Arbitrary spin-to-orbital angular momentum conversion of light. Science 358, 896–901 (2017).
Wen, D., Cadusch, J. J., Fang, Z. & Crozier, K. B. Reconsidering metasurface lasers. Nat. Photon. 15, 337–338 (2021).
Nixon, M., Redding, B., Friesem, A. A., Cao, H. & Davidson, N. Efficient method for controlling the spatial coherence of a laser. Opt. Lett. 38, 3858–3861 (2013).
Tradonsky, C., Pal, V., Chriki, R., Davidson, N. & Friesem, A. A. Talbot diffraction and Fourier filtering for phase locking an array of lasers. Appl. Opt. 56, A126–A132 (2017).
Pinnell, J. et al. Modal analysis of structured light with spatial light modulators: a practical tutorial. J. Opt. Soc. Am. A 37, C146–C160 (2020).
Longhi, S. & Feng, L. Invited article: mitigation of dynamical instabilities in laser arrays via non-Hermitian coupling. APL Photonics 3, 060802 (2018).
Arwas, G. et al. Anyonic parity-time symmetric laser. Preprint at https://arxiv.org/abs/2103.15359 (2021).
Mehuys, D., Streifer, W., Waarts, R. G. & Welch, D. F. Modal analysis of linear Talbot-cavity semiconductor lasers. Opt. Lett. 16, 823–825 (1991).
Dammann, H., Groh, G. & Kock, M. Restoration of faulty images of periodic objects by means of self-imaging. Appl. Opt. 10, 1454–1455 (1971).
El-Ganainy, R., Khajavikhan, M., Christodoulides, D. N. & Ozdemir, S. K. The dawn of non-Hermitian optics. Commun. Phys. 2, 37 (2019).
Bandres, M. A. et al. Topological insulator laser: experiments. Science 359, eaar4005 (2018).
Tsesses, S. et al. Optical skyrmion lattice in evanescent electromagnetic fields. Science 361, 993–996 (2018).
Tradonsky, C. et al. Rapid laser solver for the phase retrieval problem. Sci. Adv. 5, eaax4530 (2019).
Luo, X.-W. et al. Quantum simulation of 2D topological physics in a 1D array of optical cavities. Nat. Commun. 6, 7704 (2015).
Perez-Garcia, B., Hernandez-Aranda, R. I., Forbes, A. & Konrad, T. The first iteration of Grover’s algorithm using classical light with orbital angular momentum. J. Mod. Opt. 65, 1942–1948 (2018).
Richardson, D. J., Fini, J. M. & Nelson, L. E. Space-division multiplexing in optical fibres. Nat. Photon. 7, 354–362 (2013).
Piccardo, M. et al. Roadmap on multimode light shaping. J. Opt. 24, 013001 (2021).
Fox, A. G. & Li, T. Resonant modes in a maser interferometer. Bell Syst. Tech. J. 40, 453–488 (1961).
Learn, R. & Feigenbaum, E. Adaptive step-size algorithm for Fourier beam-propagation method with absorbing boundary layer of auto-determined width. Appl. Opt. 55, 4402–4407 (2016).
Sephton, B., Dudley, A. & Forbes, A. Revealing the radial modes in vortex beams. Appl. Opt. 55, 7830–7835 (2016).
Acknowledgements
This work has been financially supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme ‘METAmorphoses’, grant agreement no. 817794 (A.A.). This work has been supported by Fondazione Cariplo, grant no. 2019-3923 (A.A.). We thank N. Davidson, S. Mahler and S. Gadasi for useful discussions.
Author information
Authors and Affiliations
Contributions
M.P. designed the laser setup, performed the laser numerical simulations and designed the metasurface arrays. M.P. and M.d.O. carried out the experiments and modelled the OAM partitioning and coupling networks. M.d.O. designed and implemented the scheme for the topological charge analysis. A.T. and V.A. fabricated the metasurface arrays. M.P., M.d.O., A.F. and A.A. discussed the results. A.A. conceived the original idea and supervised the research.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Philippe St-Jean and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–13 and Discussion.
Supplementary Video 1
Calculated intensity (left) and phase (right) of an array of 10 × 10 vortices of topological charge L = 1 propagating in the Talbot section of the cavity. Here zT is the Talbot distance.
Supplementary Video 2
Calculated intensity (left) and phase (right) of an array of 10 × 10 vortices of topological charge L = 5 propagating in the Talbot section of the cavity. Here zT is the Talbot distance.
Supplementary Video 3
Transient showing the healing process of a topological charge defect with L = 2 (marked by a square) embedded in a metasurface array with L = 1 (right). At every round trip of the laser, we show the dynamically evolving phase profile of the vortex array. The simulation starts from a noise seed. Initially, the charge corresponding to the defect device is L = 2, but after approximately 16 round trips, the defect is healed and the charge becomes L = 1, remaining stable for any subsequent iteration (also beyond the ones shown in the video).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Piccardo, M., de Oliveira, M., Toma, A. et al. Vortex laser arrays with topological charge control and self-healing of defects. Nat. Photon. 16, 359–365 (2022). https://doi.org/10.1038/s41566-022-00986-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41566-022-00986-0
This article is cited by
-
Time localized tilted beams in nearly-degenerate laser cavities
Scientific Reports (2024)
-
Orbital angular momentum-mediated machine learning for high-accuracy mode-feature encoding
Light: Science & Applications (2024)
-
Orbital angular momentum lasers
Nature Reviews Physics (2024)
-
Optical vortex ladder via Sisyphus pumping of Pseudospin
Nature Communications (2024)
-
Optical vortex-antivortex crystallization in free space
Nature Communications (2024)