Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

An integrated broadband spectrometer on thin-film lithium niobate

Nature Photonics volume 14, pages 24–29 (2020)Cite this article

Subjects

Abstract

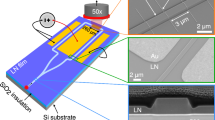
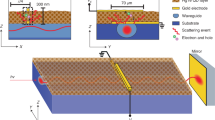
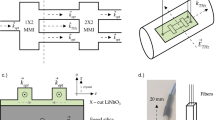
Optical spectrometry is a tool to investigate wavelength-dependent light–matter interactions and is widely used in astronomy, physics and chemistry. Integration and miniaturization of the currently bulky spectrometers will have an impact on applications where compactness and low complexity are key, such as air- and spaceborne missions. A high-resolution spectroscopy principle based on the near-field detection of a spatial standing wave inside a subwavelength waveguide has shown great promise to accomplish some of the aforementioned demands. However, small-scale devices based on this principle face strong bandwidth limitations due to undersampling of the standing wave. Here, we demonstrate an integrated single-waveguide Fourier transform spectrometer with an operational bandwidth of 500 nm in the near- and short-wavelength infrared, not relying on any moving components. The prototype device, with a footprint of less than 10 mm2, exploits the electro-optic properties of thin-film lithium niobate in order to retrieve the complete spatial interferogram.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Electro-optic sampling of the broadband interferogram.
Fig. 2: Electro-optic LN waveguide spectrometer.
Fig. 3: Monochromatic and dual-wavelength measurements.
Fig. 4: Broadband spectra.

Similar content being viewed by others

Data availability

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

References

  1. Blind, N., Le Coarer, E., Kern, P. & Gousset, S. Spectrographs for astrophotonics. Opt. Express 25, 27341–27369 (2017).

    Article  ADS  Google Scholar 

  2. Manzardo, O., Herzig, H. P., Marxer, C. R. & de Rooij, N. F. Miniaturized time-scanning Fourier transform spectrometer based on silicon technology. Opt. Lett. 24, 1705–1707 (1999).

    Article  ADS  Google Scholar 

  3. Knipp, D. et al. Silicon-based micro-Fourier spectrometer. IEEE Trans. Electron. Devices 52, 419–426 (2005).

    Article  ADS  Google Scholar 

  4. Cheben, P. et al. A high-resolution silicon-in-insulator arrayed waveguide grating microspectrometer with sub-micrometer aperture waveguides. Opt. Express 15, 2299–2306 (2007).

    Article  ADS  Google Scholar 

  5. Delâge, A. et al. Static Fourier-transform waveguide spectrometers. In 2009 11th International Conference on Transparent Optical Networks (ICTON) We.D1.1 (IEEE, 2009).

  6. Ma, X., Li, M. & He, J.-J. CMOS-compatible integrated spectrometer based on echelle diffraction grating and MSM photodetector array. IEEE Photon. J. 5, 6600807 (2013).

    Article  ADS  Google Scholar 

  7. Kyotoku, B. B. C., Chen, L. & Lipson, M. Sub-nm resolution cavity enhanced micro-spectrometer. Opt. Express 18, 102–107 (2009).

    Article  ADS  Google Scholar 

  8. Babin, S. et al. Digital optical spectrometer-on-chip. Appl. Phys. Lett. 95, 041105 (2009).

    Article  ADS  Google Scholar 

  9. Peroz, C. et al. Multiband wavelength demultiplexer based on digital planar holography for on-chip spectroscopy applications. Opt. Lett. 37, 695–697 (2012).

    Article  ADS  Google Scholar 

  10. Griffiths, P. R. & de Haseth, J. A. Fourier Transform Infrared Spectrometry (Wiley, 2007).

  11. Li, J., Lu, D.-f & Qi, Z.-m. Miniature Fourier transform spectrometer based on wavelength dependence of half-wave voltage of a LiNbO3 waveguide interferometer. Opt. Lett. 39, 3923–3926 (2014).

    Article  ADS  Google Scholar 

  12. Dong, B. et al. Nano-silicon-photonic Fourier transform infrared (FTIR) spectrometer-on-a-chip. In Conference on Lasers and Electro-Optics (CLEO) STu4I.1 (OSA, 2015).

  13. Souza, M. C. M. M., Grieco, A., Frateschi, N. C. & Fainman, Y. Fourier transform spectrometer on silicon with thermo-optic non-linearity and dispersion correction. Nat. Commun. 9, 665 (2018).

    Article  ADS  Google Scholar 

  14. Florjańczyk, M. et al. Planar waveguide spatial heterodyne spectrometer. Proc. SPIE 6796, 67963J (2007).

    Article  Google Scholar 

  15. Velasco, A. V. et al. High-resolution Fourier-transform spectrometer chip with microphotonic silicon spiral waveguides. Opt. Lett. 38, 706–708 (2013).

    Article  ADS  Google Scholar 

  16. Nedeljkovic, M. et al. Mid-infrared silicon-on-insulator Fourier-transform spectrometer chip. IEEE Photon. Technol. Lett. 28, 528–531 (2015).

    Article  ADS  Google Scholar 

  17. Le Coarer, E. et al. Wavelength-scale stationary-wave integrated Fourier-transform spectrometry. Nat. Photon. 1, 473–478 (2007).

    Article  ADS  Google Scholar 

  18. Bonneville, C. et al. SWIFTS: a groundbreaking integrated technology for high-performance spectroscopy and optical sensors. Proc. SPIE 8616, 86160M (2013).

    Article  Google Scholar 

  19. Nie, X., Ryckeboer, E., Roelkens, G. & Baets, R. CMOS-compatible broadband co-propagative stationary Fourier transform spectrometer integrated on a silicon nitride photonics platform. Opt. Express 25, A409–A418 (2017).

    Article  ADS  Google Scholar 

  20. Ferrand, J. et al. A SWIFTS operating in visible and near-infrared. Proc. SPIE 7010, 701046 (2008).

    Article  Google Scholar 

  21. Osowiecki, G. D. et al. Standing wave integrated Fourier transform spectrometer for imaging spectrometry in the near infrared. Proc. SPIE 9611, 96110P (2015).

    Article  Google Scholar 

  22. Madi, M. et al. Lippmann waveguide spectrometer with enhanced throughput and bandwidth for space and commercial applications. Opt. Express 26, 2682–2707 (2018).

    Article  ADS  Google Scholar 

  23. Ferrand, J. et al. Stationary wave integrated Fourier transform spectrometer (SWIFTS). Proc. SPIE 7604, 760414 (2010).

    Article  Google Scholar 

  24. Thomas, F. et al. Expanding sampling in a SWIFTS-Lippmann spectrometer using an electro-optic Mach–Zehnder modulator. Proc. SPIE 9516, 95160B (2015).

    Google Scholar 

  25. Loridat, J. et al. All integrated lithium niobate standing wave Fourier transform electro-optic spectrometer. J. Lightwave Technol. 36, 4900–4907 (2018).

    Article  ADS  Google Scholar 

  26. Schmidt, R. & Kaminow, I. Metal-diffused optical waveguides in LiNbO3. Appl. Phys. Lett. 25, 458–460 (1974).

    Article  ADS  Google Scholar 

  27. Thomas, F. et al. First results in near and mid IR lithium niobate-based integrated optics interferometer based on SWIFTS-Lippmann concept. J. Lightwave Technol. 32, 4338–4344 (2014).

    Article  Google Scholar 

  28. Lyons, R. G. Understanding Digital Signal Processing. (Pearson Education, 2011).

  29. Reig Escalé, M., Pohl, D., Sergeyev, A. & Grange, R. Extreme electro-optic tuning of Bragg mirrors integrated in lithium niobate nanowaveguides. Opt. Lett. 43, 1515–1518 (2018).

    Article  ADS  Google Scholar 

  30. Wang, C. et al. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 562, 101–104 (2018).

    Article  ADS  Google Scholar 

  31. He, M. et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photon. 13, 359–364 (2019).

    Article  ADS  Google Scholar 

  32. Bazzan, M. & Sada, C. Optical waveguides in lithium niobate: recent developments and applications. Appl. Phys. Rev. 2, 040603 (2015).

    Article  ADS  Google Scholar 

  33. Ji, X. et al. Ultra-low-loss on-chip resonators with sub-milliwatt parametric oscillation threshold. Optica 4, 619–624 (2017).

    Article  ADS  Google Scholar 

  34. Chang, L. et al. Thin film wavelength converters for photonic integrated circuits. Optica 3, 531–535 (2016).

    Article  ADS  Google Scholar 

  35. Ahmed, A. N. R., Shi, S., Zablocki, M., Yao, P. & Prather, D. W. Tunable hybrid silicon nitride and thin-film lithium niobate electro-optic microresonator. Opt. Lett. 44, 618–621 (2019).

    Article  ADS  Google Scholar 

  36. Chang, L. et al. Heterogeneous integration of lithium niobate and silicon nitride waveguides for wafer-scale photonic integrated circuits on silicon. Opt. Lett. 42, 803–806 (2017).

    Article  ADS  Google Scholar 

  37. Porter, C. D. & Tanner, D. B. Correction of phase errors in Fourier spectroscopy. Int. J. Infrared Millim. Waves 4, 273–298 (1983).

    Article  ADS  Google Scholar 

  38. Zgraggen, E. et al. Optical properties of waveguide-coupled nanowires for sub-wavelength detection in microspectrometer applications. J. Opt. 17, 025801 (2015).

    Article  ADS  Google Scholar 

  39. August, I., Oiknine, Y., AbuLeil, M., Abdulhalim, I. & Stern, A. Miniature compressive ultra-spectral imaging system utilizing a single liquid crystal phase retarder. Sci. Rep. 6, 23524 (2016).

    Article  ADS  Google Scholar 

  40. Hong, B., Monifi, F. & Fainman, Y. Channel dispersed Fourier transform spectrometer. Commun. Phys. 1, 34 (2018).

    Article  Google Scholar 

Download references

Acknowledgements

We acknowledge support for nanofabrication from the Scientific Center of Optical and Electron Microscopy ScopeM and from the cleanroom facilities BRNC and FIRST of ETH Zürich. This project was initially funded by the Swiss Space Office at the State Secretariat for Education, Research and Innovation, in the frame of the Mesures de Positionnement MdP2016 funding scheme. This project has received funding from the European Union’s Horizon 2020 research and innovation programme from the European Research Council under grant no. 714837 (Chi2-nano-oxides). This work was also supported by Swiss National Science Foundation grant no. 150609. We are also grateful to the Swiss Space Center for thoughtful inputs during the project progress review meetings. We thank I. Shorubalko for contributing to the prototype preparation and G. Scalari and J. Faist for helpful discussions.

Author information

Author notes

  1. These authors contributed equally: David Pohl, Marc Reig Escalé.

Authors and Affiliations

  1. Optical Nanomaterial Group, Institute for Quantum Electronics, Department of Physics, ETH Zurich, Zurich, Switzerland

    David Pohl, Marc Reig Escalé, Fabian Kaufmann, Peter Brotzer, Anton Sergeyev & Rachel Grange

  2. Micos Engineering GmbH, Dübendorf, Switzerland

    Mohammad Madi, Philippe Giaccari, Edoardo Alberti & Urs Meier

  3. European Space Agency (ESA), European Space Research and Technology Centre (ESTEC), Noordwijk, the Netherlands

    Mohammad Madi & Benedikt Guldimann

Authors
  1. David Pohl
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marc Reig Escalé
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohammad Madi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Fabian Kaufmann
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Peter Brotzer
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Anton Sergeyev
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Benedikt Guldimann
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Philippe Giaccari
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Edoardo Alberti
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Urs Meier
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Rachel Grange
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

B.G. and M.M. developed the original idea of directly combining electro-optic actuators with the waveguide spectrometers to carry out integrated interferogram scanning. M.M., A.S., U.M., E.A. and R.G. conceived the project. D.P., M.R.E., F.K. and A.S. developed the fabrication process. D.P., M.R.E., M.M., F.K., P.B. and A.S. designed the set-up and performed the experiments. P.G. and B.G. provided technical advice in the course of the project. D.P., M.R.E. and R.G. wrote the manuscript. M.M. and R.G. supervised the project. U.M. managed the administrative and financial aspects of the project.

Corresponding author

Correspondence to David Pohl.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

This file contains more information about the work and Supplementary Figs. 1–5.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pohl, D., Reig Escalé, M., Madi, M. et al. An integrated broadband spectrometer on thin-film lithium niobate. Nat. Photonics 14, 24–29 (2020). https://doi.org/10.1038/s41566-019-0529-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41566-019-0529-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing