Abstract
Quantum effects in nanoscale electronic devices promise to lead to new types of functionality not achievable using classical electronic components. However, quantum behaviour also presents an unresolved challenge facing electronics at the few-nanometre scale: resistive channels start leaking owing to quantum tunnelling. This affects the performance of nanoscale transistors, with direct source–drain tunnelling degrading switching ratios and subthreshold swings, and ultimately limiting operating frequency due to increased static power dissipation. The usual strategy to mitigate quantum effects has been to increase device complexity, but theory shows that if quantum effects can be exploited in molecular-scale electronics, this could provide a route to lower energy consumption and boost device performance. Here we demonstrate these effects experimentally, showing how the performance of molecular transistors is improved when the resistive channel contains two destructively interfering waves. We use a zinc-porphyrin coupled to graphene electrodes in a three-terminal transistor to demonstrate a >104 conductance-switching ratio, a subthreshold swing at the thermionic limit, a >7 kHz operating frequency and stability over >105 cycles. We fully map the anti-resonance interference features in conductance, reproduce the behaviour by density functional theory calculations and trace back the high performance to the coupling between molecular orbitals and graphene edge states. These results demonstrate how the quantum nature of electron transmission at the nanoscale can enhance, rather than degrade, device performance, and highlight directions for future development of miniaturized electronics.
Similar content being viewed by others
Main
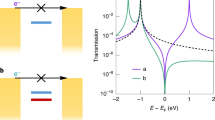
Tunnelling field-effect transistors1 and single-molecule transistors (SMTs)2 are devices where quantum effects in electron transmission, normally considered to be detrimental to the performance of transistors with nanometre dimensions3, become responsible for the function of the device. Using a single molecule as an active channel brings the benefit of synthesis with atomic precision, providing the possibility to control quantum effects through molecular design to enable high performance4, as well as leading to complementary functionalities such as thermoelectric recovery of waste heat, multistate switching or sensing5. Quantum interference (QI) is a characteristic quantum effect found in nanoscale charge transport and has been predicted to enhance transistor performance (Fig. 1)6,7,8,9,10,11,12,13. However, it is difficult to create two nanoscale quantum-coherent channels in standard conductors, because scattering and defects quickly lead to loss of electron coherence. Consequently, the practical use of QI has been almost exclusively limited to superconducting devices to obtain extremely sensitive magnetometers14, and its potential for transistors remains largely unexplored. Nevertheless, theory predicts that harnessing it is a promising route to high-performance SMTs or efficient thermoelectric generators6. Evaluating these predictions requires fundamental experimental investigation into the specific impact of QI on transistor properties.
As the source-to-drain distance, d, of a transistor approaches the nanometre scale, quantum-tunnelling-mediated transmission (ζ) through the potential energy barrier that creates an off state increases exponentially, leading to high leakage current and degrading the device subthreshold swing (Ss-th). The source–drain leakage becomes increasingly problematic at the molecular scale (<5 nm) unless interference between two coherent conduction channels acts to suppress transmission. For two quantum-coherent transport channels (with transmission coefficients ζ1, ζ2, where \(\zeta_i=|\zeta_i|{\mathrm {e}}^{-i{{\phi}_i}}\)), total transmission can be completely suppressed if |ζ1| = |ζ2| and their phase difference, Δϕ = π (through ζ2 = |ζ1 + ζ2|2 = |ζ1|2 + |ζ2|2 + 2|ζ1||ζ2|cos Δϕ), providing a route to regain desirable characteristics of mesoscopic transistor geometries even with a few-nanometre channel length.
Destructive QI (DQI) can be controlled by electrochemical gating, whereby conductance switching over two orders of magnitude has been achieved for several cycles9,10. However, electrochemical gating is relatively slow and incompatible with many practical applications. Graphene source and drain electrodes enable more versatile electrostatic gating and measurement of QI in single-molecule devices15. Furthermore, non-trivial transmission effects resulting from the coupling between the graphene density of states with molecular orbitals can sometimes enhance the device properties16,17.
To explore the use of QI in nanoelectronic devices, we employ a zinc-porphyrin with 4-ethynylaniline anchor groups at opposite (5,15) meso positions and bulky 3,5-bis(trihexylsilyl)phenyl substituents at the other two (10, 20) meso positions as an active channel (Fig. 2a; see Supplementary Section 1 for synthesis). The energy-level spacings and the chemical potentials are found to be within the experimental ranges of source–drain and gate voltages (Vsd and Vg, respectively). As a result, both the on- and off-resonance transport regimes are accessible, allowing evaluation of not only interference between orbitals but also the influence of their coupling to the reservoirs. The molecules were integrated into three-terminal molecular transistor devices by direct covalent coupling of amine groups to carboxylic acid residues on the oxidized edges of graphene electrodes, which are generated during electroburning (Methods)18. The current Isd is measured on applying Vsd, and the device behaviour can be switched using Vg (Fig. 2b).
a, Schematic representation of a graphene-based SMT. The 3,5-bis(trihexylsilyl)phenyl solubilizing groups on the lateral meso positions of the porphyrin have been replaced with H atoms for clarity. b, Device architecture. The grey-blue rectangular strip in the centre is the local platinum gate electrode under a 10 nm layer of HfO2 (transparent); the rectangular areas (grey-blue) at each end are the source and drain platinum electrodes, which are in contact with the bow-tie-shaped graphene (pink). c, Optimized junction geometry with the LDOS at the Fermi level shown in green (the isovalue is set at 0.0005). The zero-LDOS carbon atoms are highlighted in red. d, Calculated behaviour of the electronic transmission ξ as a function of energy. e, Differential conductance at T = 80 K versus Vg at Vsd = 0 mV. The conductance is plotted on a logarithmic scale as the ratio to conductance quantum, G0.
Quantum interference
The atomically defined nature of the molecular transport channel allows the prediction of the device behaviour using a combination of density functional theory (DFT) and quantum transport theory19,20. For the isolated molecule, the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) are not predicted to interfere destructively through symmetry21 or connectivity22 arguments (Supplementary Section 8). Instead, electronic interference at the graphene edges leads to DQI effects, causing zeroes in the local density of states (LDOS) at the Fermi energy at irregular edges, as shown by the red circles in Fig. 2c and in refs. 16,23. Molecular coupling between the edges of the graphene source and drain not only provides orbital resonances where device transmission is high but also maps these energy-dependent DQI effects onto the overall transmission spectrum (Fig. 2c,d) to give regions of suppressed conductance, shown in spatial visualization of the transmission pathway24 (Supplementary Section 8). The resulting full energy-dependent (E) electron transmission spectrum, ξ(E), spans over ten decades, with an asymmetric shape and an extremely pronounced dip produced by anti-resonance within the HOMO–LUMO gap (Fig. 2d). This is a surprising result: contrary to the usual case where QI is produced by the phase properties of the frontier molecular orbitals21, the anti-resonance here arises as a result of coupling between graphene edge states via molecular orbitals (Supplementary Section 8). Since the vanishing of the LDOS is a generic feature of the lead, the DQI dip should remain robust to changes in the orientation of the molecule and electrode–electrode distance (provided that through-space tunnelling is negligible).
The experimental behaviour shows the predicted features, as shown by plotting the gate dependence of the zero-bias conductance (normalized by the conductance quantum)11, Gsd = ∂Isd/∂Vsd ∝ ξ(E) (Fig. 2e) of a device (device 1; see Methods and Supplementary Table 3-1 for data on other devices). The peaks in the conductance trace arise from resonant charging of the molecule, and at Vg ≈ 0.4 V, transport occurs via a change in the occupation of the HOMO, while at Vg ≈ 1.6 V, the LUMO dominates transport, as detailed later in the full single-electron transistor characterization. The asymmetric anti-resonance feature predicted by the calculations is observed in the region between these peaks where the molecule remains neutral, showing a pronounced dip arising from the DQI effect. For a large region around Vg = 0.78 V, the conductance at the dip reaches down to below the lowest detection level of our set-up, ~10−7.0 G0, where G0 is the conductance quantum. This demonstrates that modulating Vg moves the molecular levels of the porphyrin between being on-resonance, where conductance is at local maxima, to off-resonance and complete conductance suppression.
Unimolecular transistor characteristics
The QI effects can now be used to operate a transistor device. When charging is considered, the full behaviour includes neutral molecular states, with N electrons, and oxidized (N – 1) and reduced (N + 1) states produced by varying Vg. High on/off current ratios are afforded by using the DQI-induced conductance dip as the off state and the N – 1/N resonant tunnelling channel as the on state (Fig. 3a). The full mapping of the current versus Vsd and Vg shows reproducible single-electron-transistor behaviour (Fig. 3b,c) and locally steep responses of current to gate voltage, which are advantageous for the efficient switching of the device (Fig. 3d, device 1, and Supplementary Section 3 for additional devices). Regions of low current are when the device is in the off-resonant condition where first-order tunnelling processes are suppressed by Coulomb blockade, and low residual current is carried by phase-coherent off-resonant transmission. These regions (known as Coulomb diamonds) are separated by the resonant tunnelling regions, when a molecular level is within the bias window generated by applying Vsd, where current is high (Fig. 3b). The number of electrons on the molecule is fixed within each Coulomb diamond and varies by one between adjacent diamonds2, leading to the definitions of the N – 1, N and N + 1 states mentioned above. The N – 1/N transition occurs at positive gate voltage (Vg = 0.4 V) and varies slightly between devices, indicating that there is the possibility of charge transfer from the molecule to the graphene at zero gate voltage. This effect has been observed previously for single-molecule devices25 and is because of p-doping of the graphene by the underlying substrate26, bringing the Fermi level close to, or below, the first oxidation potential of the porphyrin. The coexistence of Coulomb blockade and phase-coherent off-resonant tunnelling demonstrates that the device is in the intermediate molecule–electrode coupling (Γ) regime27,28, and from the full width at half maximum of a Coulomb peak, we find Γ = 8 meV.
a, Schematic model of the QI-based transistor, where conductance is high when a molecular level is on resonance, and low when a phase difference between two pathways suppresses transmission in the N state (the HOMO–LUMO gap). b,c, Current map (Isd versus Vsd and Vg) for devices 1 (b) and 2 (c). Device 1 is discussed in detail in the main text; devices 2–4 are characterized in Supplementary Fig. 3-4. d, Isd–Vg at Vsd = 20 mV (along the dashed line in b). e,f, Output characteristics (e) and transfer characteristics (f) of the single-porphyrin transistor; the slope of the grey line shows the thermionic limit at the measurement temperature. All measurements were done at 80 K.
In Fig. 3e,f, we focus on the transistor performance of the device through plots of the output (Isd–Vsd) and transfer characteristics (Isd–Vg) between the on and off states. Within the dip (Vg = 0.9 V), Coulomb blockade and DQI lead to extremely low currents with a resistance of ~1 GΩ, whereas on the N – 1/N resonance (Vg = 0.5 V), resonant tunnelling via the porphyrin HOMO leads to an Isd–Vsd that is approximately linear with a resistance of ~3 MΩ (Fig. 3e). Shifting the gate potential to move the device between on and off states leads to a current ratio of 103–104, depending on Vsd, and despite the differences in switching mechanism between typical MOSFETs and our SMT, the transfer characteristics have a similar shape (Fig. 3f). There is an approximately linear increase in log10(Isd) as Vg is swept from off to on before a saturation of the source–drain current; from these data, we calculate the subthreshold swing (Ss-th) of the single-molecule device. We find a value of Ss-th = 14.5 ± 0.4 mV dec−1 at Vsd = 20 mV and 80 K after adjusting for the unoptimized gate coupling parameter, αg. The value is very close to the thermionic limit—the lower limit on the subthreshold swing for a MOSFET (15.9 mV dec−1 at 80 K) that we attribute to the steepness of the transmission conferred by DQI.
Temperature-dependent behaviour
We test the switching frequency limits of the device by applying a square wave to the gate (Vg,min = 0.61 V, Vg,max = 0.76 V) with a fixed bias voltage of Vsd = 100 mV. Robust current switching is observed at kilohertz frequencies (Fig. 4a and Supplementary Fig. 4-1). The response of the current to the voltage is rounded by the RC (resistance × capacitance) time, τ, of the circuit. In this case, τ = 30 ± 1 μs, giving a rise/fall time (10% to 90% of on-state current for rise time, vice versa for fall time) of 2.2 × τrise/fall = 66 ± 2 μs and a maximum switching frequency (10% to 90%) of 1/(τrise + τfall) = 7.6 ± 0.3 kHz. The frequency is limited by the bandwidth of the current amplifier, rather than the intrinsic switching mechanism of the molecular device, as the same RC time is found by measuring the output of the circuit with a 100 MΩ resistor in place of the molecular device (Supplementary Fig. 4-1). As shown by the agreement between the transmission spectrum calculated by non-interacting Landauer theory (in which the molecular geometry is fixed) and the experimental zero-bias conductance (Fig. 2d,e), the switching mechanism is a transition from DQI-suppressed off-resonant transmission to resonant tunnelling with gate voltage and does not involve any specific conformational changes of the molecule. As sequential resonant tunnelling is first order in Γ, we estimate that the intrinsic switching frequency could be up to hf ≈ Γ ≈ 8 meV (found from fitting the left side of the resonance peak) around 1 THz. Therefore, the upper frequency limit of switching for the actual device will be limited by the time taken to charge the gate, a property that depends on the dimensions and material of the electrode. Optimizing the gate specifications is required for future device development but beyond the scope of our study of the effect of DQI on molecular transistor performance.
a, On/off switching of the device with a 2 kHz square wave applied to the gate at Vsd = 100 mV at 80 K (top) and 10 K (bottom). Longer time traces and intermediate temperatures are shown in Supplementary Fig. 6-1. b, Differential conductance map measured as a function of temperature and gate voltage at Vsd = 0 mV. c, Conductance for the on state (green), the off state (purple), and the conductance on/off ratio (orange) at Vsd = 20 mV. The error bars represent the standard deviation of the conductance in a 50 mV gate-voltage window (19 data points) around the on- and off-state value.
A map of Gsd versus T shows that the on-state resonance width remains constant below 30 K and then broadens on increasing T because of temperature effects on the electrode Fermi distributions (Fig. 4b). We also observe that the conductance on resonance begins to increase above 30 K, suggesting that thermally activated processes begin to contribute to the conduction mechanism (Fig. 4c and Supplementary Fig. 7-1). We limit our analysis to temperatures in the range of 10–100 K because of the difficulty of accounting for charge trapping and atomic-scale fluctuations at graphene edges at higher temperatures29,30. Progress in controlling these effects is crucial for increasing the operating temperature31. The DQI dip, measured at Vg ≈ 0.8 V, where the transport mechanism is solely off-resonance phase-coherent transport, remains close to our minimum detection limit in the T = 10–100 K region. The slight positive T dependence is probably the result of a reduced influence of the DQI-induced suppression, which relies on coherent electron transmission, owing to dephasing produced at higher temperatures by inelastic tunnelling and vibrations at the dynamic molecular/graphene interfaces32. The positive T dependence of both on and off states leads to a stable on/off ratio above 40 K.
Transistor performance and limits
We now examine, through the subthreshold swing, how efficient switching of the device can be achieved. The best gate control that can be achieved in a field-effect transistor is the thermionic limit that results from the exponential tails of the Fermi distributions of the electrodes (Fig. 5a)33; however, in nanodevices, performance is usually degraded further by short-channel parasitic effects. The tunnelling current in a single-molecule junction is the convolution of ξ(E) with the difference in electrode Fermi distributions \({I}_{\mathrm{sd}}\propto \int \xi (E)[\,{f}_{\mathrm{S}}({\mu }_{\mathrm{S}})-{f}_{\mathrm{d}}({\mu }_{\mathrm{d}})]{{\mathrm{d}}{{E}}}\), and so a limit on Ss-th related to T will also apply. To understand the effect of DQI on this limit, we compare our experimental measurements of Ss-th at different temperatures to a simulation of Ss-th versus T around N – 1/N using the single-level model27. The single-level model treats the molecular resonance as a Breit–Wigner resonance, and as it only considers transmission through a single channel, it cannot capture interference effects. The lifetime broadening conferred by Γ (= 8 meV, the experimentally derived value) and thermal broadening both contribute to the subthreshold swing in an SMT, ensuring that it remains above the thermionic limit at all T, with a small change where kBT ≪ Γ (where kB is the Boltzmann constant) that becomes linear as T increases (Fig. 5a). This result reveals a fundamental trade-off when designing a three-terminal nanodevice for transistor applications: a larger Γ is desirable to give high on-state currents but comes at the expense of higher off-state currents and larger subthreshold swings. Conversely, a smaller Γ puts Ss-th closer to the thermionic limit but reduces tunnelling currents to smaller values, leading to high resistances on resonance, thereby limiting on/off ratios. Utilizing DQI removes the need to compromise: DQI suppresses off-resonant phase-coherent transport, leading to the steep energy-dependent transmission through the molecular device, even with an intermediate Γ, thereby permitting a high on-state and low off-state current that can be switched by only a small change in Vg.
a, Normalized subthreshold swing at Vsd = 20 mV as a function of temperature (red circles; see Supplementary Figs. 5-1–5-9 for Ss-th calculation), plotted with the thermionic limit for a classical field-effect transistor (grey), and simulated subthreshold swing for a single-level molecular Breit–Wigner resonance without DQI (blue). b, Isd as a function of αgVg around the N – 1/N resonance; the yellow curves are experimental and the blue curves are the simulations of a Breit–Wigner resonance. The ranges to calculate the subthreshold swing are the steepest parts of the curves and are highlighted (red for experimental and blue for simulated) and demonstrate the effect of DQI to increase the magnitude of the gradient of the N state current, thereby reducing Ss-th to the thermionic limit.
This effect is demonstrated here explicitly in Fig. 5b, where DQI accounts for the difference between the simulated and experimental data. At 10 K, DQI reduces Ss-th from 14.1 mV dec−1 to 3.6 ± 0.4 mV dec−1 (thermionic limit 2.0 mV dec−1), and at 80 K, from 26.3 mV dec−1 to 14.5 ± 0.4 mV dec−1 (thermionic limit 15.9 mV dec−1). These observations show the value of DQI in the device performance: it effectively negates the additional contribution of lifetime broadening to the subthreshold swing, reducing the value to the thermionic limit, even in the intermediate coupling regime.
The general relationship between the on/off ratio and the channel length in sub-10 nm transistors (Extended Data Fig. 1) can be understood by considering the molecule as a quantum tunnelling barrier—even if the device is tuned to the off state (that is, modulating Vg to give a high tunnel barrier), devices inevitably become exponentially more transmissive with decreasing molecular length (that is, decreasing barrier width), raising off currents and decreasing the switching ratio. Without considering the phase-coherent nature of electron transmission, this leakage current fundamentally limits the transistor performance on this length scale, shown by the fit in Extended Data Fig. 1. If devices have DQI in their transmission functions, however, this need not be the case; low off currents, even with short (<1 nm) molecular lengths34, are possible if two out-of-phase coherent transport channels (such as edge states or molecular orbitals) can interfere to suppress overall device transmission. Extended Data Fig. 1 demonstrates this effect where devices at the scale of a few nanometres that utilize DQI can have properties of those with longer channel lengths. Utilizing this mechanism is a particular advantage of molecular nanoelectronics, as the energies and phase properties of orbitals are routinely engineered through molecular design and synthesis. The reduction in the on/off ratio with increasing temperature owing to increasing leakage current (Fig. 4c) is attributed to a partial quenching of interference effects32; however, a fuller understanding of the underlying mechanism is crucial to design devices that retain extremely low off currents resulting from DQI at room temperature. The numbers that we report compare favourably to previous studies of SMT properties that have yielded subthreshold swings in the range of 400–1,000 mV dec−1 (our value would be 140 mV dec−1 at room temperature, removing the adjustment for αg and linearly extrapolating from Fig. 5a). While most SMTs are characterized by a handful of cycles at a frequency below a few hertz owing to inherent timescales of electrochemical gating, we demonstrate a switching frequency of ~7 kHz, and over the course of our measurements, we switch our device over 105 times. Furthermore, previous measurements are mostly based on scanning tunneling microscopy break-junction techniques, so they involve continuous reforming of molecular junctions, with the conductance of on and off states taken as an average over many traces, rather than our measurements of repeatedly switching the same, static unimolecular device.
Conclusion
Overall, these results reveal how QI can be harnessed in devices just a few nanometres wide, in pursuit of low-power miniaturized electronics. The performances attained offer proof of concept of nanodevices in which quantum effects are used as a resource to enhance device function, rather than being a limitation. Our demonstration makes specific use of the density of states fluctuations at graphene edges, revealing a hitherto undisclosed difference from standard metal electrodes. The key challenge that remains is to develop experimental methods to prepare graphene interfaces with defined geometries, such as through Joule heating35 or coupling to chemically synthesized nanoribbons36,37. The concepts we have presented, using phase-coherent transmission, can however be translated to a series of new compounds and device architectures that are designed to optimally exploit QI. The mild fabrication method allows using a wide range of chemical compounds to create these nanoscale transistors, opening the path to the creation of multifunctional devices, for example, with optical or spintronic properties, where interference can be used to control multiple effects at the same time.
Methods
Substrate fabrication
On an n-doped silicon wafer with a 300-nm-thick SiO2 layer, the gate electrode (3 μm wide) was defined by optical lithography with lift-off resist and electron-beam (e-beam) evaporation of titanium (5 nm) and platinum (15 nm). Next, an atomic-layer-deposition-grown dielectric layer of HfO2 (10 nm) was deposited. Finally, source and drain contact electrodes separated by a 7 μm gap (gap centred with the gate) were defined by optical lithography with lift-off resist and e-beam evaporation of titanium (5 nm) and platinum (45 nm). Wafers were diced into 10 × 10 mm chips, each containing 874 devices.
Graphene patterning
Poly(methyl methacrylate) (PMMA)-protected chemical-vapour-deposition-grown graphene was wet-transferred to the substrate. The PMMA was removed in warm acetone for 3 h. The graphene tape with a bow-tie-shaped structure was patterned by e-beam lithography with bilayer lift-off resist (PMMA495 and PMMA950) and thermal evaporation of aluminium (50 nm). After lift-off, the graphene on unexposed areas (not covered by aluminium) was etched with oxygen plasma. The aluminium was subsequently removed by aqueous NaOH solution (1.0 g in 50 ml water). The sample was finally immersed in warm acetone overnight to remove any residual PMMA. Scanning electron microscopy images can be found in Supplementary Section 2.
Graphene nanogaps
Graphene nanogaps were prepared by feedback-controlled electroburning of the graphene bow-tie shape until the resistance of the tunnel junction exceeds 1.3 GΩ (10−7 G0) (see Supplementary Section 2 for electroburning curves)38,39. HfO2 has a high dielectric constant, and in combination with the weaker screening of the gate field by using graphene in place of bulky three-dimensional metallic electrodes (most commonly used in molecular junctions)40, this yields a high gating efficiency. The empty nanogaps were characterized by measuring a current map as a function of bias voltage (Vsd) and gate voltage (Vg) at room temperature to exclude devices containing residual graphene quantum dots41. Only clean devices were selected for further measurement (see Supplementary Figs. 3-1, 3-3 and 3-6 for before and after current maps of the devices presented here).
Molecular junctions, measurements and device numbers
The mechanism of graphene breakdown under electroburning in air is oxidation18, and the oxygen-containing functional groups that are thus formed at the edges can be used to engineer the junction by covalent binding42,43,44. Single-molecule devices are fabricated using a condensation reaction between molecular amine groups and carboxylic groups on the edge of the graphene nanogap to form amide bonds44. Chips with freshly prepared graphene nanogaps were immersed in 0.5 ml dry NEt3, after which 20 mg of the amide coupling reagent, hexafluorophosphate azabenzotriazole tetramethyl uronium, was added. Then, 0.5 ml of a dry CH2Cl2 solution of ZnP (0.2 mmol l−1) was added. The mixture was then left at room temperature in the dark for 48–72 h. After the reaction, the chip was washed with CH2Cl2 and isopropyl alcohol and blown dry with nitrogen. Then the chip containing molecular devices was connected to a chip holder via wire bonding, loaded in an Oxford Instruments 4 K PuckTester and cooled to cryogenic temperatures (4–100 K) for detailed measurements. All current (Isd) maps and traces presented in the main text and supplementary files are unprocessed. Conductance data (Gsd) were calculated by applying a Savitzky–Golay filter (window length, 15; order, 5 or 7) to Isd and then differentiating to give Gsd = ∂Isd/∂Vsd. Subthreshold swings (Ss-th) were calculated from the steepest part of a log10(Isd) versus Vg trace (over two decades). The measurement was repeated six times for each temperature (see Supplementary Figs. 5-1–5-9 for the traces) and then averaged. The error reported is twice the standard deviation.
In total, we measured the current maps (Isd versus Vsd, Vg) before and after the amide coupling procedure for 440 devices over six chips at room temperature. Sixteen of these devices (3.6%) showed large conductance increases and resonant transport features only after the coupling procedure, indicating that a molecular device had been formed. Most of the other devices showed either resonant transport features before molecular deposition or open-circuit behaviour after the coupling, in line with the results from π-stacking single-molecule graphene devices, discussed in depth in ref. 41. Four chips that had a molecular device were wire-bonded and loaded into an Oxford Instruments PuckTester cryostat for low-temperature measurements. All four molecular devices (devices 1–4) measured at low temperature showed a DQI dip around Vg = 0 V. Two devices (devices 1 and 2—shown in the main text) were subjected to detailed transistor characterization over a range of temperatures. The charge transport properties of devices 3 and 4 are shown in Supplementary Fig. 3-7, and the performance of all the four devices are compared in Supplementary Table 3-1.
Theoretical calculations
Geometry optimizations were carried out using Gaussian 16 (ref. 45) for the isolated molecular structure using the University of Oxford Advanced Research Computing (ARC) facility, and SIESTA was used for the graphene-based junctions46. Transmission spectra were calculated from the Hamiltonian and overlap matrices of the DFT calculation of the junction using the GOLLUM47 quantum transport code. The atom-to-atom transmission pathways were obtained by using DFT combined with the non-equilibrium Green’s function method, implemented in the QuantumATK S-2021.06-SP1 software package20. Full details are given in Supplementary Section 8.
Data availability
All the data supporting the findings of this study are available within the article, its Supplementary Information or from the corresponding authors upon request.
References
Appenzeller, J., Lin, Y. M., Knoch, J. & Avouris, P. Band-to-band tunneling in carbon nanotube field-effect transistors. Phys. Rev. Lett. 93, 196805 (2004).
Perrin, M. L., Burzuri, E. & van der Zant, H. S. Single-molecule transistors. Chem. Soc. Rev. 44, 902–919 (2015).
Yuan, T. et al. CMOS scaling into the nanometer regime. Proc. IEEE 85, 486–504 (1997).
Heinrich, A. J. et al. Quantum-coherent nanoscience. Nat. Nanotechnol. 16, 1318–1329 (2021).
Aradhya, S. V. & Venkataraman, L. Single-molecule junctions beyond electronic transport. Nat. Nanotechnol. 8, 399–410 (2013).
Li, Y., Mol, J. A., Benjamin, S. C. & Briggs, G. A. Interference-based molecular transistors. Sci. Rep. 6, 33686 (2016).
Liu, J., Huang, X., Wang, F. & Hong, W. Quantum interference effects in charge transport through single-molecule junctions: detection, manipulation, and application. Acc. Chem. Res. 52, 151–160 (2019).
Andrews, D. Q., Solomon, G. C., Van Duyne, R. P. & Ratner, M. A. Single molecule electronics: increasing dynamic range and switching speed using cross-conjugated species. J. Am. Chem. Soc. 130, 17309–17319 (2008).
Bai, J. et al. Anti-resonance features of destructive quantum interference in single-molecule thiophene junctions achieved by electrochemical gating. Nat. Mater. 18, 364–369 (2019).
Li, Y. et al. Gate controlling of quantum interference and direct observation of anti-resonances in single molecule charge transport. Nat. Mater. 18, 357–363 (2019).
Lambert, C. J. Basic concepts of quantum interference and electron transport in single-molecule electronics. Chem. Soc. Rev. 44, 875–888 (2015).
Hong, W. et al. An MCBJ case study: the influence of pi-conjugation on the single-molecule conductance at a solid/liquid interface. Beilstein J. Nanotechnol. 2, 699–713 (2011).
Guedon, C. M. et al. Observation of quantum interference in molecular charge transport. Nat. Nanotechnol. 7, 305–309 (2012).
Fagaly, R. L. Superconducting quantum interference device instruments and applications. Rev. Sci. Instrum. 77, 101101 (2006).
Chen, Z. et al. Phase-coherent charge transport through a porphyrin nanoribbon. J. Am. Chem. Soc. 145, 15265–15274 (2023).
Carrascal, D., García-Suárez, V. M. & Ferrer, J. Impact of edge shape on the functionalities of graphene-based single-molecule electronics devices. Phys. Rev. B 85, 195434 (2012).
Gehring, P. et al. Distinguishing lead and molecule states in graphene-based single-electron transistors. ACS Nano 11, 5325–5331 (2017).
El Abbassi, M. et al. From electroburning to sublimation: substrate and environmental effects in the electrical breakdown process of monolayer graphene. Nanoscale 9, 17312–17317 (2017).
Lambert, C. J. Quantum Transport in Nanostructures and Molecules: An Introduction to Molecular Electronics (IOP, 2021).
Smidstrup, S. et al. QuantumATK: an integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Matter 32, 015901 (2020).
Yoshizawa, K. An orbital rule for electron transport in molecules. Acc. Chem. Res. 45, 1612–1621 (2012).
Markussen, T., Stadler, R. & Thygesen, K. S. The relation between structure and quantum interference in single molecule junctions. Nano Lett. 10, 4260–4265 (2010).
Garcia-Suarez, V. M. et al. Spin signatures in the electrical response of graphene nanogaps. Nanoscale 10, 18169–18177 (2018).
Solomon, G. C., Herrmann, C., Hansen, T., Mujica, V. & Ratner, M. A. Exploring local currents in molecular junctions. Nat. Chem. 2, 223–228 (2010).
Limburg, B. et al. Charge-state assignment of nanoscale single-electron transistors from their current-voltage characteristics. Nanoscale 11, 14820–14827 (2019).
Song, S. M. & Cho, B. J. Investigation of interaction between graphene and dielectrics. Nanotechnology 21, 335706 (2010).
Gehring, P., Thijssen, J. M. & van der Zant, H. S. J. Single-molecule quantum-transport phenomena in break junctions. Nat. Rev. Phys. 1, 381–396 (2019).
Moth-Poulsen, K. & Bjornholm, T. Molecular electronics with single molecules in solid-state devices. Nat. Nanotechnol. 4, 551–556 (2009).
Fried, J. P. et al. Large amplitude charge noise and random telegraph fluctuations in room-temperature graphene single-electron transistors. Nanoscale 12, 871–876 (2020).
Balandin, A. A. Low-frequency 1/f noise in graphene devices. Nat. Nanotechnol. 8, 549–555 (2013).
Pósa, L. et al. Noise diagnostics of graphene interconnects for atomic-scale electronics. npj 2D Mater. Appl. 5, 57 (2021).
Hartle, R., Butzin, M., Rubio-Pons, O. & Thoss, M. Quantum interference and decoherence in single-molecule junctions: how vibrations induce electrical current. Phys. Rev. Lett. 107, 046802 (2011).
Sze, S. M., Li, Y. & Ng, K. K. Physics of Semiconductor Devices (Wiley, 2021).
Garner, M. H. et al. Comprehensive suppression of single-molecule conductance using destructive sigma-interference. Nature 558, 415–419 (2018).
Jia, X. et al. Controlled formation of sharp zigzag and armchair edges in graphitic nanoribbons. Science 323, 1701–1705 (2009).
Zhang, J. et al. Contacting individual graphene nanoribbons using carbon nanotube electrodes. Nat. Electron. 6, 572–581 (2023).
Niu, W. et al. Exceptionally clean single-electron transistors from solutions of molecular graphene nanoribbons. Nat. Mater. 22, 180–185 (2023).
Lau, C. S., Mol, J. A., Warner, J. H. & Briggs, G. A. Nanoscale control of graphene electrodes. Phys. Chem. Chem. Phys. 16, 20398–20401 (2014).
Prins, F. et al. Room-temperature gating of molecular junctions using few-layer graphene nanogap electrodes. Nano Lett. 11, 4607–4611 (2011).
Thomas, J. O. et al. Understanding resonant charge transport through weakly coupled single-molecule junctions. Nat. Commun. 10, 4628 (2019).
Limburg, B. et al. Anchor groups for graphene-porphyrin single-molecule transistors. Adv. Funct. Mater. 28, 1803629 (2018).
Xu, Q. et al. Single electron transistor with single aromatic ring molecule covalently connected to graphene nanogaps. Nano Lett. 17, 5335–5341 (2017).
Cao, Y. et al. Building high-throughput molecular junctions using indented graphene point contacts. Angew. Chem. Int. Ed. 51, 12228–12232 (2012).
Guo, X. et al. Covalently bridging gaps in single-walled carbon nanotubes with conducting molecules. Science 311, 356–359 (2006).
Gaussian 16 Rev. C.01 (Guassian, Inc., 2016).
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 14, 2745–2779 (2002).
Ferrer, J. et al. GOLLUM: a next-generation simulation tool for electron, thermal and spin transport. New J. Phys. 16, 093029 (2014).
Brooke, R. J. et al. Single-molecule electrochemical transistor utilizing a nickel-pyridyl spinterface. Nano Lett. 15, 275–280 (2015).
Darwish, N. et al. Observation of electrochemically controlled quantum interference in a single anthraquinone-based norbornylogous bridge molecule. Angew. Chem. Int. Ed. 51, 3203–3206 (2012).
Jia, C. et al. Quantum interference mediated vertical molecular tunneling transistors. Sci. Adv. 4, eaat8237 (2018).
Diez-Perez, I. et al. Gate-controlled electron transport in coronenes as a bottom-up approach towards graphene transistors. Nat. Commun. 1, 31 (2010).
Franklin, A. D. et al. Sub-10 nm carbon nanotube transistor. Nano Lett. 12, 758–762 (2012).
Franklin, A. D. & Chen, Z. Length scaling of carbon nanotube transistors. Nat. Nanotechnol. 5, 858–862 (2010).
Weitz, R. T. et al. High-performance carbon nanotube field effect transistors with a thin gate dielectric based on a self-assembled monolayer. Nano Lett. 7, 22–27 (2007).
Lin, Y. M., Appenzeller, J., Knoch, J. & Avouris, P. High-performance carbon nanotube field-effect transistor with tunable polarities. IEEE Trans. Nanotechnol. 4, 481–489 (2005).
Acknowledgements
We acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out part of this work (https://doi.org/10.5281/zenodo.22558). The work was supported by the EPSRC (grants EP/X026876/1, EP/N017188/1 and EP/R029229/1), and the EU through EIC-Pathfinder-101099676-4D-NMR and ERC-CoG-773048-MMGNRs grants. J.A.M. acknowledges funding from the Royal Academy of Engineering and a UKRI Future Leaders Fellowship, grant no. MR/S032541/1. We thank J. Cremers for help with the synthesis and F. Kong for helpful discussions.
Author information
Authors and Affiliations
Contributions
The experiments were conceived by J.O.T. and Z.C. with support from G.A.D.B., C.J.L., J.A.M., L.B. and H.L.A. Z.C. performed the graphene patterning and fabrication of molecular devices and undertook the charge transport measurements with input from A.G. S.L.W. and J.O.T. synthesized and characterized the compounds under the supervision of H.L.A. J.B. prepared the device substrates. I.M.G. and Z.C. performed the DFT calculations under the supervision of C.J.L. J.O.T., L.C. and Z.C. analysed the data. J.O.T. and Z.C. wrote the paper. All authors discussed the results and edited the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Nanotechnology thanks Nadim Darwish, Christian Nijhuis and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Overview of quantum-Interference-enhanced transistor performance.
Scatter plot of ON/OFF ratio and molecular lengths for a number of molecular and carbon nanotube transistor devices (148, 29, 349, 410, 550, 651, 752, 853, 954, 1055 and this work, with the normalization for αg removed); SAM = self-assembled monolayer, CNT = carbon nanotube. Marker colours represent the device subthreshold swing normalised by the thermionic limit at the measurement temperature, which is room temperature except for those specifically marked. Markers with red outlines represent devices that have DQI in their transmission, the black line below 10 nm is a fit to the data points without interference.
Supplementary information
Supplementary Information
Chemical synthesis, Fabrication images, Additional transport measurements, RC time calculation, Subthreshold swing measurement, Temperature-dependent switching, Temperature dependence of resonant tunnelling and DFT calculations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, Z., Grace, I.M., Woltering, S.L. et al. Quantum interference enhances the performance of single-molecule transistors. Nat. Nanotechnol. 19, 986–992 (2024). https://doi.org/10.1038/s41565-024-01633-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-024-01633-1
This article is cited by
-
Graphene edge interference improves single-molecule transistors
Nature Nanotechnology (2024)