Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

In-memory factorization of holographic perceptual representations

Nature Nanotechnology volume 18, pages 479–485 (2023)Cite this article

Subjects

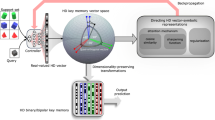
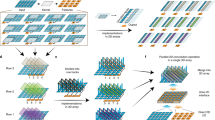
Abstract

Disentangling the attributes of a sensory signal is central to sensory perception and cognition and hence is a critical task for future artificial intelligence systems. Here we present a compute engine capable of efficiently factorizing high-dimensional holographic representations of combinations of such attributes, by exploiting the computation-in-superposition capability of brain-inspired hyperdimensional computing, and the intrinsic stochasticity associated with analogue in-memory computing based on nanoscale memristive devices. Such an iterative in-memory factorizer is shown to solve at least five orders of magnitude larger problems that cannot be solved otherwise, as well as substantially lowering the computational time and space complexity. We present a large-scale experimental demonstration of the factorizer by employing two in-memory compute chips based on phase-change memristive devices. The dominant matrix–vector multiplication operations take a constant time, irrespective of the size of the matrix, thus reducing the computational time complexity to merely the number of iterations. Moreover, we experimentally demonstrate the ability to reliably and efficiently factorize visual perceptual representations.

This is a preview of subscription content, access via your institution

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Factorization of perceptual representations using the in-memory factorizer.
Fig. 2: Stochastic similarity computation, sparse activations and limit cycles.
Fig. 3: Operational capacity of the stochastic in-memory factorizer with sparse activations.
Fig. 4: Experimental realization of the in-memory factorizer.

Data availability

The data that support the findings of this study are available via Zenodo at https://zenodo.org/record/7599430. Source data are provided with this paper.

Code availability

Our code is available via GitHub at https://github.com/IBM/in-memory-factorizer.

References

  1. Feldman, J. The neural binding problem(s). Cogn. Neurodyn. 7, 1–11 (2013).

    Article  Google Scholar 

  2. Land, E. H. & McCann, J. J. Lightness and retinex theory. J. Opt. Soc. Am. 61, 1–11 (1971).

    Article  CAS  Google Scholar 

  3. Barrow, H. G. & Tenenbaum, J. M. in Computer Vision Systems 3–26 (Academic Press, 1978).

  4. Adelson, E. & Pentland, A. in The Perception of Shading and Reflectance 409–424 (Cambridge Univ. Press, 1996).

  5. Barron, J. T. & Malik, J. Shape, illumination and reflectance from shading. IEEE Trans. Pattern Anal. Mach. Intell. 37, 1670–1687 (2015).

    Article  Google Scholar 

  6. Memisevic, R. & Hinton, G. E. Learning to represent spatial transformations with factored higher-order Boltzmann machines. Neural Comput. 22, 1473–1492 (2010).

    Article  Google Scholar 

  7. Burak, Y., Rokni, U., Meister, M. & Sompolinsky, H. Bayesian model of dynamic image stabilization in the visual system. Proc. Natl Acad. Sci. USA 107, 19525–19530 (2010).

    Article  CAS  Google Scholar 

  8. Cadieu, C. F. & Olshausen, B. A. Learning intermediate-level representations of form and motion from natural movies. Neural Comput. 24, 827–866 (2012).

    Article  Google Scholar 

  9. Anderson, A. G., Ratnam, K., Roorda, A. & Olshausen, B. A. High-acuity vision from retinal image motion. J. Vision 20, 34 (2020).

    Article  Google Scholar 

  10. Smolensky, P. Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artif. Intell. 46, 159–216 (1990).

    Article  Google Scholar 

  11. Jackendoff, R. Foundations of Language: Brain, Meaning, Grammar, Evolution (Oxford Univ. Press, 2002).

  12. Hummel, J. E. & Holyoak, K. J. Distributed representations of structure: a theory of analogical access and mapping. Psychol. Rev. 104, 427–466 (1997).

    Article  Google Scholar 

  13. Kanerva, P. in Advances in Analogy Research: Integration of Theory and Data from the Cognitive, Computational and Neural Sciences 164–170 (New Bulgarian Univ., 1998).

  14. Kanerva, P. Pattern completion with distributed representation. In International Joint Conference on Neural Networks 1416–1421 (IEEE, 1998).

  15. Plate, T. A. Analogy retrieval and processing with distributed vector representations. Expert Syst. Int. J. Knowledge Eng. Neural Netw. 17, 29–40 (2000).

    Google Scholar 

  16. Gayler, R. W. & Levy, S. D. A distributed basis for analogical mapping: new frontiers in analogy research. In New Frontiers in Analogy Research, Second International Conference on the Analogy 165–174 (New Bulgarian University Press, 2009).

  17. Gayler, R. W. Vector symbolic architectures answer Jackendoff’s challenges for cognitive neuroscience. In Joint International Conference on Cognitive Science 133–138 (Springer, 2003).

  18. Plate, T. A. Holographic reduced representations. IEEE Trans. Neural Netw. 6, 623–641 (1995).

    Article  CAS  Google Scholar 

  19. Plate, T. A. Holographic Reduced Representations: Distributed Representation for Cognitive Structures (Stanford Univ., 2003).

  20. Kanerva, P. Hyperdimensional computing: an introduction to computing in distributed representation with high-dimensional random vectors. Cogn. Comput. 1, 139–159 (2009).

    Article  Google Scholar 

  21. Frady, E. P., Kent, S. J., Olshausen, B. A. & Sommer, F. T. Resonator networks, 1: an efficient solution for factoring high-dimensional, distributed representations of data structures. Neural Comput. 32, 2311–2331 (2020).

    Article  Google Scholar 

  22. Hersche, M., Zeqiri, M., Benini, L., Sebastian, A. & Rahimi, A. A neuro-vector-symbolic architecture for solving Raven’s progressive matrices. Nat. Mach. Intell. https://doi.org/10.1038/s42256-023-00630-8 (2023).

  23. Lanza, M. et al. Memristive technologies for data storage, computation, encryption and radio-frequency communication. Science 376, eabj9979 (2022).

    Article  CAS  Google Scholar 

  24. Sebastian, A., Le Gallo, M., Khaddam-Aljameh, R. & Eleftheriou, E. Memory devices and applications for in-memory computing. Nat. Nanotechnol. 15, 529–544 (2020).

    Article  CAS  Google Scholar 

  25. Wang, Z. et al. Resistive switching materials for information processing. Nat. Rev. Mater. 5, 173–195 (2020).

    Article  CAS  Google Scholar 

  26. Kent, S. J., Frady, E. P., Sommer, F. T. & Olshausen, B. A. Resonator networks, 2: factorization performance and capacity compared to optimization-based methods. Neural Comput. 32, 2332–2388 (2020).

    Article  Google Scholar 

  27. Wong, H.-S. P. & Salahuddin, S. Memory leads the way to better computing. Nat. Nanotechnol. 10, 191–194 (2015).

    Article  CAS  Google Scholar 

  28. Chua, L. Resistance switching memories are memristors. Appl. Phys. A 102, 765–783 (2011).

    Article  CAS  Google Scholar 

  29. Shin, J. H., Jeong, Y. J., Zidan, M. A., Wang, Q. & Lu, W. D. Hardware acceleration of simulated annealing of spin glass by RRAM crossbar array. In Proc. IEEE International Electron Devices Meeting 3.3.1–3.3.4 (IEEE, 2018).

  30. Bojnordi, M. N. & Ipek, E. Memristive Boltzmann machine: a hardware accelerator for combinatorial optimization and deep learning. In Proc. IEEE International Symposium on High Performance Computer Architecture 1–13 (IEEE, 2016).

  31. Mahmoodi, M. R., Prezioso, M. & Strukov, D. B. Versatile stochastic dot product circuits based on nonvolatile memories for high performance neurocomputing and neurooptimization. Nat. Commun. 10, 5113 (2019).

    Article  CAS  Google Scholar 

  32. Borders, W. A. et al. Integer factorization using stochastic magnetic tunnel junctions. Nature 573, 390–393 (2019).

    Article  CAS  Google Scholar 

  33. Wan, W. et al. 33.1 A 74 TMACS/W CMOS-RRAM neurosynaptic core with dynamically reconfigurable dataflow and in-situ transposable weights for probabilistic graphical models. In Proc. IEEE International Solid-State Circuits Conference 498–500 (IEEE, 2020).

  34. Kumar, S., Strachan, J. P. & Williams, R. S. Chaotic dynamics in nanoscale NbO2 Mott memristors for analogue computing. Nature 548, 318–321 (2017).

    Article  CAS  Google Scholar 

  35. Cai, F. et al. Power-efficient combinatorial optimization using intrinsic noise in memristor Hopfield neural networks. Nat. Electron. 3, 409–418 (2020).

    Article  Google Scholar 

  36. Yang, K. et al. Transiently chaotic simulated annealing based on intrinsic nonlinearity of memristors for efficient solution of optimization problems. Sci. Adv. 6, eaba9901 (2020).

    Article  CAS  Google Scholar 

  37. Khaddam-Aljameh, R. et al. Hermes core—a 14nm CMOS and PCM-based in-memory compute core using an array of 300ps/LSB linearized CCO-based ADCs and local digital processing. In 2021 Symposium on VLSI Circuits 1–2 (IEEE, 2021).

  38. Tuma, T., Pantazi, A., Le Gallo, M., Sebastian, A. & Eleftheriou, E. Stochastic phase-change neurons. Nat. Nanotechnol. 11, 693–699 (2016).

    Article  CAS  Google Scholar 

  39. Le Gallo, M., Krebs, D., Zipoli, F., Salinga, M. & Sebastian, A. Collective structural relaxation in phase-change memory devices. Adv. Electron. Mater. 4, 1700627 (2018).

    Article  Google Scholar 

  40. Le Gallo, M. & Sebastian, A. An overview of phase-change memory device physics. J. Phys. D Appl. Phys. 53, 213002 (2020).

    Article  Google Scholar 

  41. Zhang, C., Gao, F., Jia, B., Zhu, Y. & Zhu, S.-C. RAVEN: a dataset for relational and analogical visual reasoning. In Proc. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 5312–5322 (IEEE, 2019).

  42. Kent, S. Multiplicative Coding and Factorization in Vector Symbolic Models of Cognition. PhD thesis, Univ. California (2020).

  43. Kleyko, D. et al. Integer factorization with compositional distributed representations. In Proc. 9th Annual Neuro-Inspired Computational Elements Conference 73–80 (ACM, 2022).

  44. Li, J. et al. Low angle annular dark field scanning transmission electron microscopy analysis of phase change material. In Proc. International Symposium for Testing and Failure Analysis 2021 206–210 (ASM, 2021).

Download references

Acknowledgements

This work is supported by the IBM Research AI Hardware Center and by the Swiss National Science Foundation (SNF) (grant no. 200800). We thank M. Le Gallo for the technical help; K. Brew and J. Li for assistance with TEM imaging of PCM devices; and V. Narayanan, C. Apte and R. Haas for managerial support.

Author information

Authors and Affiliations

  1. IBM Research—Zurich, Rüschlikon, Switzerland

    Jovin Langenegger, Geethan Karunaratne, Michael Hersche, Abu Sebastian & Abbas Rahimi

  2. Department of Information Technology and Electrical Engineering, ETH Zürich, Zürich, Switzerland

    Jovin Langenegger, Geethan Karunaratne, Michael Hersche & Luca Benini

Authors
  1. Jovin Langenegger
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Geethan Karunaratne
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Michael Hersche
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Luca Benini
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Abu Sebastian
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Abbas Rahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.L., G.K., M.H., A.S. and A.R. conceived the idea and designed the experiments. J.L. performed the experiments and characterization. J.L., A.S. and A.R. wrote the paper, with input from all the authors. All the authors provided critical comments and analyses.

Corresponding authors

Correspondence to Abu Sebastian or Abbas Rahimi.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Nanotechnology thanks Mario Lanza and Yuchao Yang for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Desirable range of noise.

The aggregated noise corresponding to the programming noise, drift variability, and read noise in the PCM devices affects (a) the accuracy of factorization, and (b) the number of iterations to converge. The optimal range for the standard deviation of the noise lies between 0.293μS and 1.277μS. As indicated by the green vertical line, the level of noise observed in the experimental crossbar array lies within the desirable range of noise.

Source data

Supplementary information

Supplementary Information

Supplementary Notes 1–4, Tables 1–3 and Figs. 1–5.

This video showcases one application of the proposed in-memory factorizer. Here the visual attributes of an image are disentangled using a front-end convolutional neural network and a back-end in-memory factorizer.

Source data

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Langenegger, J., Karunaratne, G., Hersche, M. et al. In-memory factorization of holographic perceptual representations. Nat. Nanotechnol. 18, 479–485 (2023). https://doi.org/10.1038/s41565-023-01357-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41565-023-01357-8

This article is cited by

Search

Advanced search

Quick links

Find nanotechnology articles, nanomaterial data and patents all in one place. Visit Nano by Nature Research