Abstract
Control over charge carrier density provides an efficient way to trigger phase transitions and modulate the optoelectronic properties of materials. This approach can also be used to induce topological transitions in the optical response of photonic systems. Here we report a topological transition in the isofrequency dispersion contours of hybrid polaritons supported by a two-dimensional heterostructure consisting of graphene and α-phase molybdenum trioxide. By chemically changing the doping level of graphene, we observed that the topology of polariton isofrequency surfaces transforms from open to closed shapes as a result of doping-dependent polariton hybridization. Moreover, when the substrate was changed, the dispersion contour became dominated by flat profiles at the topological transition, thus supporting tunable diffractionless polariton propagation and providing local control over the optical contour topology. We achieved subwavelength focusing of polaritons down to 4.8% of the free-space light wavelength by using a 1.5-μm-wide silica substrate as an in-plane lens. Our findings could lead to on-chip applications in nanoimaging, optical sensing and manipulation of energy transfer at the nanoscale.
Similar content being viewed by others
Main
The control of charge carrier concentration by either electrostatic or chemical means has been widely studied as a way to induce phase transitions of different nature, such as structural in transition metal dichalcogenides1,2,3,4, ferromagnetic in high-Curie-temperature manganites5,6,7,8,9,10 and topological in engineered materials11,12,13,14, with potential application in the development of active electronic phase-change devices15. In this context, a collection of different phases in magic-angle bilayer graphene has been achieved by changing its carrier density16. Similar concepts have been theoretically explored in photonics using hyperbolic metamaterials composed of subwavelength structures, such as a periodic array of graphene ribbons17 or a stack of graphene dielectric layers18, in which a topological transition in the isofrequency dispersion contour can occur by changing the doping level of graphene. However, these hyperbolic metamaterials rely on a strong anisotropy of the effective permittivity tensor, which is ultimately limited by spatial nonlocal effects that can hinder a practical verification of this concept.
Recently, a twisted stack of two α-phase molybdenum trioxide (α-MoO3) films was explored to control the topology of the isofrequency dispersion contour of phonon polaritons (PhPs) by varying the relative twist angle between the two α-MoO3 layers19,20,21,22. Owing to the in-plane anisotropy of the permittivity within the reststrahlen band from 816 to 976 cm−1, the real part of the permittivity is positive along the [001] direction but negative along the [100] direction23,24, a property that renders α-MoO3 a natural hyperbolic material supporting in-plane hyperbolic PhPs25,26. The low-loss in-plane hyperbolic PhPs in α-MoO3 thus emerge as an ideal platform to explore further possibilities of doping-driven and electrically tunable topological transitions in photonics.
In this work we have achieved the control of polariton dispersion in a van der Waals (vdW) heterostructure composed of an α-MoO3 film covered with monolayer graphene by changing the doping level of the latter. We observed the polariton dispersion contour to vary from hyperbolic (open) to elliptic (closed) on increasing the doping level of graphene, leading to the emergence of a mode dominated by its graphene plasmon polariton (GPP) component propagating along the [001] direction at high doping levels. The nature of the polaritons emerging at high doping in the heterostructure evolved from GPP to PhP when moving from the [001] to [100] α-MoO3 crystallographic direction. In addition, when the vdW heterostructure was placed on top of a gold substrate instead of SiO2, a rather flattened dispersion contour was obtained due to a topological transition. As an application, we have designed an in-plane subwavelength focusing device by engineering the substrate.
Tunable topological polaritons in heterostructures
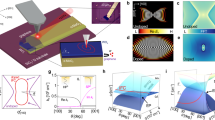
A schematic of our proposed structure is shown in Fig. 1, where a 150-nm-thick vdW heterostructure is placed on top of either a SiO2 (Fig. 1a) or gold (Fig. 1d) substrate. We were particularly interested in the reststrahlen band II of α-MoO3 extending over the frequency range of 816 to 976 cm−1, where the permittivity (ε) components along the [100], [001] and [010] crystal directions satisfy εx < 0, εy > 0 and εz > 0, respectively (Supplementary Fig. 1a)23,24. As a result, the in-plane PhPs in natural α-MoO3 exhibit a hyperbolic dispersion contour. To illustrate dynamic control of the dispersion contour topology of the in-plane hybrid plasmon–phonon polaritons in our structure, we present in Fig. 1b several calculated dispersion contours on SiO2 at different graphene Fermi energies (EF) under a fixed representative incident free-space wavelength of λ0 = 10.99 μm (frequency of 910 cm−1). As the graphene Fermi energy increases from 0 to 0.7 eV, the opening angle φ of the hyperbolic sectors gradually increases due to a change in the PhP wavelength when varying the dielectric environment, and eventually the dispersion contour changes its character from a hyperbolic (open) to elliptic (closed) shape. Note that the Fermi energy at which this topological transition occurs is conditioned to the appearance of well-defined graphene plasmons along the [001] direction at λ0 when increasing its doping level27,28,29,30. When the substrate was changed from SiO2 to gold, we found flatter dispersion contours (Fig. 1e) due to the stronger effect of screening provided by the gold substrate. Tunable polariton canalization and diffractionless propagation were thus expected.
a,d, Illustration of the graphene/α-MoO3 vdW heterostructure used in this study, supported on SiO2 (a) and gold (d) substrates. b,e, Calculated isofrequency dispersion contours of hybrid polaritons on a 300-nm-thick SiO2 substrate (b) and a 60-nm-thick gold substrate (e) at a fixed incident frequency of 910 cm−1 (λ0 = 10.99 µm) for different graphene Fermi energies ranging from 0 to 0.7 eV and an α-MoO3 film thickness of 150 nm. φ indicates the opening angle of the hyperbolic sectors. kx and ky are the momenta of polariton along the x and y crystal directions of α-MoO3, while k0 is the momentum of light in free space. c,f, Numerically simulated field distributions (real part of the z out-of-plane component of the electric field, Re{Ez}) of hybrid polaritons on SiO2 (c) and gold (f) substrates for several graphene doping levels at a fixed incident frequency of 910 cm−1, as launched by a dipole placed 100 nm above the origin.
Numerically simulated field distributions of hybrid polaritons for different graphene Fermi energies are shown in Fig. 1c,f. At EF = 0 eV, the polaritons of the heterostructure on a SiO2 substrate exhibit a hyperbolic wavefront, similar to that of the PhPs in α-MoO3. In contrast, the wavelength of the polaritons on a gold substrate is highly compressed, whereas their opening angle is increased. On increasing the doping level to EF = 0.2 eV, a topological transition takes place. The wavelength of the hybrid polaritons is increased compared with the undoped case, and we can still observe a hyperbolic wavefront along the x direction on the SiO2 substrate. Moreover, for the hybrid polaritons on the gold substrate (Fig. 1f), highly collimated and directive hybrid polaritons propagating along the x direction can be observed as a result of a rather flattened dispersion contour. At EF = 0.3 eV, a hyperbolic wavefront of hybrid polaritons can still be observed along the x direction with the SiO2 substrate, but another mode with an elliptic wavefront propagating along the y direction also emerges. With the gold substrate, the wavefront of the hybrid polaritons is dominated by a fine crescent shape along the x direction. At a higher doping level (EF = 0.7 eV), the dispersion contours for the hybrid polaritons on both SiO2 and gold substrates display an elliptic-like shape (Fig. 1b,e). As a consequence, we can find modes propagating anisotropically in the x–y plane (for additional theoretical analyses, see Supplementary Figs. 2–4 and other works31,32,33).
Experimental observation of topological transitions
We used infrared nanoimaging to visualize the propagating polaritons in the graphene/α-MoO3 heterostructures (Supplementary Fig. 5) and verify the above theoretical predictions (Fig. 2a–c,g–i). In this technique, upon p-polarized infrared light illumination, the resonant gold antenna efficiently launches hybrid polaritons (Supplementary Fig. 6), originating in the nanoscale concentrated fields at the two endpoints. While scanning the sample, the real part of the scattered light electric field (Re{ES}) is recorded simultaneously with the topography, making it possible to directly map the vertical near-field components of the hybrid polariton wavefronts launched by the antenna (for more details on near-field image analysis, see Supplementary Figs. 7 and 8).
a–c, Experimentally measured polariton near-field amplitude (S3) images with graphene doping EF = 0 eV (a), EF = 0.3 eV (b) and EF = 0.7 eV (c). The polaritons were launched by a gold antenna. The α-MoO3 film was placed on top of a 300 nm SiO2/500 μm Si substrate. d–f, Absolute value of the spatial Fourier transforms (FTs) of the experimental near-field images shown in a–c, respectively, revealing the isofrequency contours of hybrid polaritons. The grey curves represent calculated isofrequency contours. g–i, Experimentally measured polariton near-field amplitude (S3) images with graphene doping EF = 0 eV (g), EF = 0.3 eV (h) and EF = 0.7 eV (i) for an α-MoO3 film placed on a 60 nm Au/500 μm Si substrate. The canalized wavefronts were measured at a graphene Fermi energy close to the value at which the topological transition occurs (h), showing deep-subwavelength and diffractionless polariton propagation. j–l, Absolute value of the FTs of the experimental near-field images in g–i, respectively. The grey curves show the calculated isofrequency contours. The α-MoO3 thickness was 140 nm in all panels. The incident light wavelength was fixed at λ0 = 11.11 μm (900 cm−1). Each colour scale applies to all images in the respective column.
To visualize the polariton wavefronts34,35, we imaged antenna-launched polaritons in the heterostructure at several intermediate graphene Fermi energies in the range EF = 0–0.7 eV (Supplementary Fig. 9). We first investigated hybrid polaritons in an undoped sample with EF = 0 eV, which revealed a precise hyperbolic wavefront (Fig. 2a,g) for both SiO2 and gold substrates, consistent with previous results for a single film of α-MoO3 as a result of the hyperbolic dispersion contour. Next, we examined the optical response of a sample with a relatively high doping level (EF = 0.3 eV) on a SiO2 substrate at the same incidence frequency. The image in Fig. 2b shows that the measured wavefronts remain hyperbolic along the x direction, while fringes around the antenna appear in the y direction, indicating that the dispersion contour has evolved into a closed shape, as shown in Fig. 1b and Supplementary Fig. 2. In contrast, the sample on a gold substrate shows a nearly flat wavefront for EF = 0.3 eV (Fig. 2h), indicating a topological transition in the dispersion contour along the x direction. On increasing the doping level further to EF = 0.7 eV, only elliptical wavefronts were observed (Fig. 2c,i) for samples on both SiO2 and gold substrates, denoting a rather rounded anisotropic dispersion contour. The corresponding Fourier transforms of the experimental near-field images (Fig. 2d–f,j–l) and simulated near-field distributions (Supplementary Figs. 3 and 4) further confirmed the transformation of the dispersion contour with increasing doping level of graphene. Notably, our extracted experimental polariton wave vectors k = 2π/λp (dotted symbols in Supplementary Fig. 10; λp is the wavelength of hybrid polaritons) match quite well the calculated dispersion diagrams in all cases.
Low levels of disorder or minor imperfections in the heterostructure should not substantially affect the control capability (Supplementary Fig. 13). In addition, the thickness of α-MoO3 determines the influence of the dielectric environment (here, the substrate), which should not exceed the skin depth of hybrid polaritons (Supplementary Fig. 14).
Close to EF = 0.3 eV, where the dispersion contour is rather flat, as shown in Fig. 2h, the propagation of hybrid polaritons appears to be firmly guided along the x direction, yielding a highly directive and diffractionless behaviour. Furthermore, this type of polariton canalization can be found over a wide range of frequencies and different thicknesses of α-MoO3 (Supplementary Fig. 11) due to the inherent robustness of the topological transition. The line profiles (vertical cuts along the y direction) across the amplitude of the canalization mode give a full-width at half-maximum (FWHM) of around 115 ± 5 nm (~λ0/95, where λ0 is the free-space wavelength), as shown in Supplementary Fig. 12.
Launching and manipulation of hybrid polaritons with tailored antenna
By rotating the long axis of the antenna by an angle θ with respect to the y direction, we could selectively launch and manipulate hybrid polaritons with different in-plane wave vectors. The launching contribution from our antenna can be decomposed into four parts: two endpoints acting as resonant dipoles and two parallel edges behaving as line dipoles (and assimilated to linear arrays of discrete dipoles).
Figure 3a shows for a sample with a low doping level (EF = 0.1 eV) that, at θ = 0°, the field pattern of the exciting hybrid polaritons exhibits vertical fringes parallel to the long axis of the antenna, dominated by the line dipole contributions generated by the edges. Note that the two endpoint dipoles are not well excited when θ = 0° because the polarization direction of the incident light is not aligned with the long axis of the antenna. We can extract the polariton wave vector from the fringes parallel to this long axis. As θ increases from 0 to 90°, the wavefronts produced by the two endpoints gradually show up and interact with those produced by the edges. In the regime with rotation angles θ ≤ 40°, the distance between adjacent fringes parallel to the antenna edge is reduced from 590 to 380 nm, from which we can obtain the wave vector k perpendicular to the antenna. The extracted wave vectors are shown by red symbols in Fig. 3e, matching quite well the calculated dispersion contour (solid curves; more details on the extraction analysis are provided in Supplementary Fig. 16). When θ ≥ 60° (~φ, the opening angle indicated in Fig. 3e), there are no fringes parallel to the edge of the antenna because polariton propagation is prohibited along that direction, judging from the dispersion contour, and the field pattern is dominated by the hyperbolic wavefronts produced by the two endpoints of the antenna. The simulated field patterns shown in Fig. 3b corroborate these experimental observations for different rotation angles.
a,c, Experimentally measured near-field amplitude (S3) images of hybrid polaritons launched by gold antennas with orientation angle θ in the 0–90° range (Supplementary Fig. 15) for a graphene Fermi energy EF = 0.1 eV (a) and EF = 0.7 eV (c) at a light frequency of 910 cm−1. b,d, Numerically simulated near-field distributions (Re{Ez}, evaluated 20 nm above the surface of the heterostructure) corresponding to the measured results shown in a and c, respectively. e,f, Isofrequency dispersion contours extracted from the experimental data in a and c, respectively (red symbols), compared with the calculated hyperbolic dispersion contour (black solid curves) for an opening angle φ. The green arrows illustrate the direction of the exciting polariton wave vector k perpendicular to the long axis of the gold antenna. The α-MoO3 thickness was 207 nm in all panels. Scale bars in a–d, 2 μm. The error bars were extracted from four sets of measurements on the in situ sample (Supplementary Fig. 15). The artefacts observed in c and not in a can be attributed to the grain boundaries of polycrystalline graphene prepared by chemical vapour deposition43.
For a sample with a high doping level (EF = 0.7 eV, Fig. 3c), the antenna can generate polaritons propagating in all directions within the x–y plane when the polarization direction of the incident light is along the long axis of the antenna. Due to the in-plane anisotropy, the excited field patterns are therefore different for the various rotation angles explored in the range from 0 to 90°. The simulated field patterns (Fig. 3d) again agree well with our experimental observations. The polariton wave vectors can still be extracted from the measured fringes perpendicular to the antenna, shown as red symbols in Fig. 3f, which also match quite well the calculated dispersion contour (solid curves). Note that, at EF = 0.3 eV, the field patterns of hybrid polaritons launched by antennas with different rotation angles (from 0 to 45°) all lie strictly along the x direction (Supplementary Fig. 17) due to the flattening of the dispersion contour, which leads to directional canalization at this graphene Fermi energy. More details on the extraction of polariton wave vectors from experiments can be found in Supplementary Figs. 16 and 18.
Partial focusing of polaritons by substrate engineering
As the dispersion contour of the hybrid polaritons can be modified substantially by controlling the dielectric environment, we engineered the substrate for the heterostructure to manipulate the in-plane propagation of hybrid polaritons. The design is illustrated in Fig. 4a, where the heterostructure lies on top of a substrate composed of a Au–SiO2–Au in-plane sandwich structure. This substrate was used to locally engineer the isofrequency dispersion contour (Fig. 4b). The central SiO2 film, with a width of 1.5 μm, serves as an in-plane flat lens to partially focus the incident polaritons (with a wave vector ki and a Poynting vector Pi along the normal of the contour in Fig. 4b) generated by an antenna on top of the left gold substrate. When the hybrid polaritons cross the boundary between the gold and SiO2 substrates, due to the change in the detailed shape of the dispersion contour, negative refraction can occur at the boundary, with the y component of the wave vector being conserved, whereas the sign of the y component of the transmitted Poynting vector Pt is opposite to that of the incident Pi, as illustrated in Fig. 4b. This leads to a partial focusing of the polaritons (Fig. 4c). Supplementary Fig. 19 shows the evolution of the negative refraction of hybrid polaritons at different Fermi energies of graphene.
a, Schematic of the design, where the heterostructure lies on top of a substrate composed of a Au–SiO2–Au in-plane sandwich structure. b, Isofrequency dispersion contours of hybrid polaritons for Au and SiO2 substrates at 910 cm−1 (λ0 = 10.99 μm). The shaded areas highlight the convex and concave dispersion contours in the region around the x axis on the gold and SiO2 substrates, respectively. With a wave vector inside the shaded area, negative refraction can happen at the Au–SiO2 interface when the polaritons on the gold substrate propagate towards that interface. The scheme for negative refraction is illustrated by further showing the incident wave vector ki and the Poynting vector Pi, together with the resulting transmitted kt and Pt. c, Experimentally measured near-field amplitude (S3) image of hybrid polaritons showing partial focusing in the system shown in a. The central SiO2 film was 1.5 µm wide and served as an in-plane flat lens. The antenna was located 1.0 µm away from the left Au–SiO2 interface. d, Experimentally measured hybrid polaritons on a Au substrate, as a control to c. Scale bar indicates 1.5 μm and also applies to c. e, Near-field profiles for the sections marked by the red (A) and blue (C) vertical dashed lines in c and d, respectively. The black dashed curves are Gaussian fittings. WA and WC indicate the full width at half maximum (FWHM) of profiles A and C, respectively. f, Near-field profiles of the sections marked by red (B) and blue (D) horizontal dashed lines in c and d, respectively. SB1, SB2, SD1 and SD2 represent the electric-field intensity at each fringe. The graphene was doped to EF = 0.6 eV and the α-MoO3 thickness was 320 nm.
The measured antenna-launched polariton near-field distributions for the heterostructure on gold and SiO2 substrates are shown in Fig. 4d and Supplementary Figs. 20 and 21, respectively. On the gold substrate, only elliptical wavefronts are observed around the antenna, denoting a convex dispersion contour in the region around the x axis. In contrast, on the SiO2 substrate (Supplementary Fig. 21), wavefronts are hyperbolic along the x direction and elliptic along the y direction around the antenna, indicating a closed concave shape of the dispersion contour near the x axis. These measurements are consistent with our previous experimental results shown in Figs. 2 and 3, and also, they match quite well the isofrequency contours shown in Fig. 4b.
Furthermore, we launched hybrid polaritons towards the Au–SiO2–Au in-plane sandwich substrate from the left gold part by light coupling to an antenna prepared in that region. The resulting near-field distribution is shown in Fig. 4c (for more details, see Supplementary Figs. 20 and 21). When polaritons having elliptical wavefronts on the left gold substrate cross the boundary between the gold and SiO2 substrates, the Poynting vector of the polaritons refracts on the same side of the boundary-normal direction, therefore producing what is known as negative refraction due to the change in the detailed shape of the dispersion contour, which ultimately leads to partial focusing of the incident polaritons. Indeed, Fig. 4c shows the formation of a focal spot close to the right Au–SiO2 interface. The numerically simulated z out-of-plane component of the electric field distributions (Re{Ez}) shown in Supplementary Fig. 22 further corroborate the experimental findings. The red curve in Fig. 4e shows the spatial distribution of the electric field amplitude at the focal spot, demonstrating a high wavelength compression towards a FWHM of 520 nm along the y direction. This focal spot size is less than 1/21 of the corresponding illumination wavelength, thus emphasizing a deep subwavelength focusing effect (for more details, see Supplementary Figs. 23 and 24).
To estimate the intensity enhancement of the observed partial focusing, we extracted the spatial distribution of the electric field from the propagation profile (Fig. 4f). The intensity enhancement ξ is given by the square of the ratio of the electric field at the focal spot to that without focusing, \(\xi = \left( {\frac{{S_{{\mathrm{B}}2}/S_{{\mathrm{B}}1}}}{{S_{{\mathrm{D}}2}/S_{{\mathrm{D}}1}}}} \right)^2 = 4.5\). SB1, SB2, SD1, and SD2 represent the near-field intensity at each fringe. Note that the focusing effect can be further enhanced by improving the flatness of the interface, as its structural inhomogeneity inevitably introduces undesired reflection, scattering and radiative losses of the incident polaritons (for more details, see Supplementary Figs. 25–27).
Conclusions
We have experimentally demonstrated that the topology of the isofrequency dispersion contours for the hybrid polaritons supported in a heterostructure composed of a graphene sheet on top of an α-MoO3 layer can be substantially modified by chemically changing the doping level of graphene, with the contour topology being transformed from open to closed shapes over a broad frequency range. A flat dispersion contour appears at the topological transition, which supports a highly directive and diffractionless polariton propagation, resulting in a tunable canalization mode controlled by the doping level of graphene. We anticipate that electrical gating could be used to control the doping level in future studies36,37. Furthermore, through the appropriate choice of substrate for the heterostructure, we were also able to engineer the dispersion contour to exhibit even flatter profiles (for example, by using a gold substrate). This property has allowed us to design a deep-subwavelength device for in-plane focusing of hybrid polaritons, where negative refractive occurs at the boundary between two different substrates. Our study opens promising possibilities to tune topological polaritonic transitions in low-dimensional materials38,39,40 with potential applications in optical imaging, sensing and the control of spontaneous emission at the nanoscale18.
Note added in proof: While preparing this manuscript, two related theoretical and experimental studies on the tuning of highly anisotropic phonon polaritons in graphene and α-MoO3 vdW structures were reported41,42.
Methods
Nanofabrication of the devices
High-quality α-MoO3 flakes were mechanically exfoliated from bulk crystals synthesized by the chemical vapour deposition (CVD) method19 and then transferred onto either commercial 300 nm SiO2/500 μm Si wafers (SVM) or gold substrates using a deterministic dry transfer process with a polydimethylsiloxane (PDMS) stamp. CVD-grown monolayer graphene on copper foil was transferred onto the α-MoO3 samples using the poly(methyl methacrylate) (PMMA)-assisted method following our previous report44.
The launching efficiency of the resonant antenna is mainly determined by its geometry, together with a trade-off between the optimum size and illumination frequency45,46. We designed the gold antenna with a length of 3 μm and a thickness of 50 nm, which provided a high launching efficiency over the spectral range from 890 to 950 cm−1 within the α-MoO3 reststrahlen band. Alternatively, a thicker antenna with a stronger z component of the electric field could be used to launch the polaritons more efficiently in future studies. Note that narrow antennas (50-nm width) were used to prevent their shapes from affecting the polariton wavefronts, especially when their propagation is canalized (such as in Figs. 2 and 3), while wider antennas (250-nm width) were used to obtain a higher launching efficiency and observe polaritons propagating across the SiO2–Au interface in our experiments (for example, Fig. 4).
Gold antenna arrays were patterned on selected α-MoO3 flakes using 100 kV electron-beam lithography (Vistec 5000+ES) on an approximately 350 nm PMMA950K lithography resist. Electron-beam evaporation was subsequently used to deposit 5 nm Ti and 50 nm Au in a vacuum chamber at a pressure of <5 × 10−6 torr to fabricate the Au antennas. Electron-beam evaporation was also used to deposit a 60-nm-thick gold film onto a low-doped Si substrate. To remove any residual organic material, samples were immersed in a hot acetone bath at 80 °C for 25 min and then subjected to gentle rinsing with isopropyl alcohol (IPA) for 3 min, followed by drying with nitrogen gas and thermal baking (for more details on the fabrication and characterization of the Au–SiO2–Au in-plane sandwich structure, see Supplementary Figs. 26 and 27).
The samples were annealed in a vacuum to remove most of the dopants from the wet transfer process and then transferred to a chamber filled with NO2 gas to achieve different doping levels by surface adsorption of gas molecules47. The graphene Fermi energy could be controlled by varying the gas concentration and doping time, achieving values as high as ~0.7 eV (Supplementary Fig. 9). This gas-doping method provides excellent uniformity, reversibility and stability. Indeed, Raman mapping of a gas-doped graphene sample demonstrated the high uniformity of the method (Supplementary Fig. 9). As the deposition of NO2 gas molecules on the graphene surface occurs by physical adsorption, the topological transition of hybrid polaritons in graphene/α-MoO3 heterostructures can be reversed by controlling the gas doping. For example, after gas doping, the Fermi energy of graphene could be lowered from 0.7 to 0 eV by vacuum annealing at 150 °C for 2 h. The sample could subsequently be re-doped to reach another on-demand Fermi energy (Supplementary Fig. 28). It should be noted that the graphene Fermi energy only decreases from 0.7 to 0.6 eV after being left for 2 weeks under ambient conditions, which demonstrates the high stability of the doping effect (Supplementary Fig. 29). Note that chemical doping has been demonstrated to be an effective way to tune the characteristics of polaritons, such as their strength and in-plane wavelength48,49,50,51.
Scanning near-field optical microscopy measurements
A scattering scanning near-field optical microscope (Neaspec) equipped with a wavelength-tunable quantum cascade laser (890–2,000 cm−1) was used to image optical near fields. The atomic force microscopy (AFM) tip of the microscope was coated with gold, resulting in an apex radius of ~25 nm (NanoWorld), and the tip-tapping frequency and amplitudes were set to ~270 kHz and ~30–50 nm, respectively. The laser beam was directed towards the AFM tip, with lateral spot sizes of ~25 μm under the tip, which were sufficient to cover the antennas as well as a large area of the graphene/α-MoO3 samples. Third-order harmonic demodulation was applied to the near-field amplitude images to strongly suppress background noise.
In our experiments, the p-polarized plane-wave illumination (electric field Einc) impinged at an angle of 60° relative to the tip axis52. To avert any effects caused by the light polarization direction relative to the crystallographic orientation of α-MoO3, which is optically anisotropic, the in-plane projection of the polarization vector coincided with the x direction ([100] crystal axis) of α-MoO3 (Supplementary Fig. 6). Supplementary Fig. 30 shows the method used to extract antenna-launched hybrid polaritons from the complex background signals observed when the polaritons propagate across a Au–SiO2–Au in-plane structure to realize partial focusing.
Calculation of polariton dispersion and isofrequency dispersion contours (IFCs) of hybrid plasmon–phonon polaritons
The transfer matrix method was adopted to calculate the dispersion and IFCs of hybrid plasmon–phonon polaritons in graphene/α-MoO3 heterostructures. Our theoretical model was based on a three-layer structure: layer 1 (z > 0, air) is a cover layer, layer 2 (0 > z > –dh, graphene/α-MoO3) is an intermediate layer and layer 3 (z < –dh, SiO2 or Au) is a substrate where z is the value of the vertical axis and dh is the thickness of α-MoO3 (Supplementary Fig. 31). Each layer was regarded as a homogeneous material represented by the corresponding dielectric tensor. The air and substrate layers were modelled by isotropic tensors diag{εa,s} (ref. 53). The α-MoO3 film was modelled by an anisotropic diagonal tensor diag{εx, εy, εz}, where εx, εy and εz are the permittivity components along the x, y and z axes, respectively. Also, monolayer graphene was located on top of α-MoO3 at z = 0 and described as a zero-thickness current layer characterized by a frequency-dependent surface conductivity taken from the local random-phase approximation model54,55:
which depends on the Fermi energy EF, the inelastic relaxation time τ and the temperature T; the relaxation time is expressed in terms of the graphene Fermi velocity vF = c/300 and the carrier mobility μ, with \(\tau = \mu E_{\mathrm{F}}/ev_{\mathrm{F}}^2\); e is the elementary charge; kB is the Boltzmann constant; ℏ is the reduced Planck constant; and ω is the illumination frequency.
Given the strong field confinement produced by the structure under consideration, we only needed to consider transverse magnetic (TM) modes, because transverse electric (TE) components contribute negligibly. The corresponding p-polarization Fresnel reflection coefficient rp of the three-layer system admits the analytical expression
Here, rjk denotes the reflection coefficient of the j–k interface for illumination from medium j, with j,k = 1–3; \({\it{\epsilon }}_t^{(j)}\) is the tangential component of the in-plane dielectric function of layer j for a propagation wave vector kp(θ) (where θ is the angle relative to the x axis), which can be expressed as \({\it{\epsilon }}_t^{(j)} = {\it{\epsilon }}_x^{(j)}\mathop {{\cos }}\nolimits^2 \theta + {\it{\epsilon }}_y^{(j)}\mathop {{\sin }}\nolimits^2 \theta\) (where \({\it{\epsilon }}_x^{(j)}\) and \({\it{\epsilon }}_y^{(j)}\) are the diagonal dielectric tensor components of layer j along the x and y axes, respectively); \(k_z^{\left( j \right)} = \sqrt {\varepsilon _t^{\left( j \right)}\frac{{\omega ^2}}{{c^2}} - \frac{{\varepsilon _t^{\left( j \right)}}}{{\varepsilon _z^{\left( j \right)}}}q^2}\) is the out-of-plane wave vector, with \({\it{\epsilon }}_z^{(j)}\) being the dielectric function of layer j along the z axis; and Z0 is the vacuum impedance.
We find the polariton dispersion relation q(ω,θ) when the denominator of equation (2) is zero:
For simplicity, we considered a system with small dissipation, so that the maxima of Im{rp} (see colour plots in Supplementary Figure 10) approximately solve the condition given by equation (8), and therefore produce the sought-after dispersion relation q(ω,θ) (see additional discussion in Supplementary Note 1).
Electromagnetic simulations
The electromagnetic fields around the antennas were calculated by a finite-elements method using the COMSOL package. In our experiments, both tip and antenna launching were investigated. For the former, the sharp metallic tip was illuminated by an incident laser beam. The tip acted as a vertical optical antenna, converting the incident light into a strongly confined near field below the tip apex, which can be regarded as a vertically oriented point dipole located at the tip apex. This localized near field provided the necessary momentum to excite polaritons. Consequently, we modelled the tip as a vertical z-oriented oscillating dipole in our simulations (Fig. 1c,f), a procedure that has been widely used for tip-launched polaritons in vdW materials56. For the antenna launching, the gold antenna can provide strong near fields of opposite polarity at the two endpoints, thus delivering high-momentum near-field components that match the wave vector of the polaritons and excite propagating modes in the graphene/α-MoO3 heterostructure45,46. Our simulations of polariton excitation by means of antennas, such as in Fig. 3b,d, incorporated the same geometrical design as in the experimental structures.
We also used a dipole polarized along the z direction to launch polaritons, and the distance between the dipole and the uppermost surface of the sample was set to 100 nm. We obtained the distribution of the real part of the out-of-plane electric field (Re{Ez}) over a plane 20 nm above the surface of graphene. The boundary conditions were set to perfectly matching layers. Graphene was modelled as a transition interface with a conductivity described by the local random-phase approximation model (see above)55,57. We assumed a graphene carrier mobility of 2,000 cm2 V–1 s–1. Supplementary Fig. 1c,d shows the permittivity of SiO2 and Au, respectively, at the mid-infrared wavelengths used.
Data availability
The data that support the findings of this study are available within the paper and the Supplementary Information. Other relevant data are available from the corresponding authors upon reasonable request. Source data are provided with this paper.
Code availability
The code that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Kappera, R. et al. Phase-engineered low-resistance contacts for ultrathin MoS2 transistors. Nat. Mater. 13, 1128–1134 (2014).
Wang, Y. et al. Structural phase transition in monolayer MoTe2 driven by electrostatic doping. Nature 550, 487–491 (2017).
Zheng, Y. R. et al. Doping-induced structural phase transition in cobalt diselenide enables enhanced hydrogen evolution catalysis. Nat. Commun. 9, 2533 (2018).
Zhang, F. et al. Electric-field induced structural transition in vertical MoTe2-and Mo1-xWxTe2-based resistive memories. Nat. Mater. 18, 55–61 (2019).
Huang, M. et al. Voltage control of ferrimagnetic order and voltage-assisted writing of ferrimagnetic spin textures. Nat. Nanotechnol. 16, 981–988 (2021).
Walter, J. et al. Voltage-induced ferromagnetism in a diamagnet. Science 6, eabb7721 (2020).
Zheng, L. M. et al. Ambipolar ferromagnetism by electrostatic doping of a manganite. Nat. Commun. 9, 1897 (2018).
Jiang, S. et al. Controlling magnetism in 2D CrI3 by electrostatic doping. Nat. Nanotechnol. 13, 549–553 (2018).
Walter, J. et al. Giant electrostatic modification of magnetism via electrolyte-gate-induced cluster percolation in La1-xSrxCoO3-δ. Phys. Rev. Mater. 2, 111406 (2018).
Kim, D. et al. Tricritical point and the doping dependence of the order of the ferromagnetic phase transition of La1-xCaxMnO3. Phys. Rev. Lett. 89, 227202 (2002).
Chen, B. et al. Intrinsic magnetic topological insulator phases in the Sb doped MnBi2Te4 bulks and thin flakes. Nat. Commun. 10, 4469 (2019).
Sajadi, E. et al. Gate-induced superconductivity in a monolayer topological insulator. Science 362, 922–925 (2018).
Chen, Z. et al. Carrier density and disorder tuned superconductor-metal transition in a two-dimensional electron system. Nat. Commun. 9, 4008 (2018).
Liu, Q. et al. Switching a normal insulator into a topological insulator via electric field with application to phosphorene. Nano Lett. 15, 1222–1228 (2015).
Chen, Y. et al. Phase engineering of nanomaterials. Nat. Rev. Chem. 4, 243–256 (2020).
Choi, Y. et al. Correlation-driven topological phases in magic-angle twisted bilayer graphene. Nature 589, 536–541 (2021).
Gomez-Diaz, J. S. et al. Hyperbolic plasmons and topological transitions over uniaxial metasurfaces. Phys. Rev. Lett. 114, 233901 (2015).
Yu, R. et al. Ultrafast topological engineering in metamaterials. Phys. Rev. Lett. 125, 037403 (2020).
Chen, M. et al. Configurable phonon polaritons in twisted α-MoO3. Nat. Mater. 19, 1307–1311 (2020).
Duan, J. et al. Twisted nano-optics: manipulating light at the nanoscale with twisted phonon polaritonic slabs. Nano Lett. 20, 5323–5329 (2020).
Hu, G. et al. Topological polaritons and photonic magic angles in twisted α-MoO3 bilayers. Nature 582, 209–213 (2020).
Zheng, Z. et al. Phonon polaritons in twisted double-layers of hyperbolic van der Waals crystals. Nano Lett. 20, 5301–5308 (2020).
Zhang, Q. et al. Hybridized hyperbolic surface phonon polaritons at α-MoO3 and polar dielectric interfaces. Nano Lett. 21, 3112–3119 (2021).
Duan, J. et al. Enabling propagation of anisotropic polaritons along forbidden directions via a topological transition. Sci. Adv. 7, eabf2690 (2021).
Ma, W. et al. In-plane anisotropic and ultra-low-loss polaritons in a natural van der Waals crystal. Nature 562, 557–562 (2018).
Zheng, Z. et al. A mid-infrared biaxial hyperbolic van der Waals crystal. Sci. Adv. 5, eaav8690 (2019).
Chen, J. et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 487, 77–81 (2012).
Fei, Z. et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 487, 82–85 (2012).
Ni, G. et al. Fundamental limits to graphene plasmonics. Nature 557, 530–533 (2018).
Woessner, A. et al. Highly confined low-loss plasmons in graphene–boron nitride heterostructures. Nat. Mater. 14, 421–425 (2015).
Bapat, A. et al. Gate tunable light–matter interaction in natural biaxial hyperbolic van der Waals heterostructures. Nanophotonics 11, 2329–2340 (2022).
Yadav, A. et al. Tunable phonon-plasmon hybridization in α-MoO3–graphene based van der Waals heterostructures. Opt. Express 29, 33171–33183 (2021).
Hajian, H. et al. Hybrid surface plasmon polaritons in graphene coupled anisotropic van der Waals material waveguides. J. Phys. D 54, 455102 (2021).
Li, P. et al. Infrared hyperbolic metasurface based on nanostructured van der Waals materials. Science 359, 892–896 (2018).
Xiong, L. et al. Programmable Bloch polaritons in graphene. Sci. Adv. 7, eabe8087 (2021).
Zhao, W. et al. Efficient Fizeau drag from Dirac electrons in monolayer graphene. Nature 594, 517–521 (2021).
Dai, S. et al. Graphene on hexagonal boron nitride as a tunable hyperbolic metamaterial. Nat. Nanotechnol. 10, 682–686 (2015).
Zhang, Q. et al. Interface nano-optics with van der Waals polaritons. Nature 597, 187–195 (2021).
Low, T. et al. Polaritons in layered two-dimensional materials. Nat. Mater. 16, 182–194 (2017).
Sternbach, A. et al. Programmable hyperbolic polaritons in van der Waals semiconductors. Science 371, 617–620 (2021).
Álvarez-Pérez, G. et al. Active tuning of highly anisotropic phonon polaritons in van der Waals crystal slabs by gated graphene. ACS Photonics 9, 383–390 (2022).
Yali, Z. et al. Tailoring topological transition of anisotropic polaritons by interface engineering in biaxial crystals. Nano Lett. 22, 4260–4268 (2022).
Fei, Z. et al. Electronic and plasmonic phenomena at graphene grain boundaries. Nat. Nanotechnol. 8, 821–825 (2013).
Hu, H. et al. Far-field nanoscale infrared spectroscopy of vibrational fingerprints of molecules with graphene plasmons. Nat. Commun. 7, 12334 (2016).
Alonso-González, P. et al. Controlling graphene plasmons with resonant metal antennas and spatial conductivity patterns. Science 344, 1369–1373 (2014).
Pons-Valencia, P. et al. Launching of hyperbolic phonon-polaritons in h-BN slabs by resonant metal plasmonic antennas. Nat. Commun. 10, 3242 (2019).
Hu, H. et al. Gas identification with graphene plasmons. Nat. Commun. 10, 1131 (2019).
Taboada-Gutierrez, J. et al. Broad spectral tuning of ultra-low-loss polaritons in a van der Waals crystal by intercalation. Nat. Mater. 19, 964–968 (2020).
Wu, Y. et al. Chemical switching of low-loss phonon polaritons in α-MoO3 by hydrogen intercalation. Nat. Commun. 11, 2646 (2020).
Zheng, Z. et al. Chemically-doped graphene with improved surface plasmon characteristics: an optical near-field study. Nanoscale 8, 16621–16630 (2016).
Zheng, Z. et al. Highly confined and tunable hyperbolic phonon polaritons in van der Waals semiconducting transition metal oxides. Adv. Mater. 30, e1705318 (2018).
Amenabar, I. et al. Structural analysis and mapping of individual protein complexes by infrared nanospectroscopy. Nat. Commun. 4, 2890 (2013).
Kischkat, J. et al. Mid-infrared optical properties of thin films of aluminum oxide, titanium dioxide, silicon dioxide, aluminum nitride, and silicon nitride. Appl. Opt. 51, 6789–6798 (2012).
Wunsch, B. et al. Dynamical polarization of graphene at finite doping. New J. Phys. 8, 318 (2006).
Nikitin, A. et al. Real-space mapping of tailored sheet and edge plasmons in graphene nanoresonators. Nat. Photonics 10, 239–243 (2016).
Luan, Y. et al. Tip- and plasmon-enhanced infrared nanoscopy for ultrasensitive molecular characterizations. Phys. Rev. Appl. 13, 034020 (2020).
Epstein, I. et al. Far-field excitation of single graphene plasmon cavities with ultracompressed mode volumes. Science 368, 1219–1223 (2020).
Acknowledgements
We acknowledge P. Alonso-González and J. Duan (Departamento de Física, Universidad de Oviedo) for valuable discussions and constructive comments. This work was supported by the National Key Research and Development Program of China (grant no. 2021YFA1201500, to Q.D.; 2020YFB2205701, to H.H.), the National Natural Science Foundation of China (grant nos. 51902065, 52172139 to H.H.; 51925203, U2032206, 52072083 and 51972072, to Q.D.), Beijing Municipal Natural Science Foundation (grant no. 2202062, to H.H.) and the Strategic Priority Research Program of Chinese Academy of Sciences (grant nos. XDB30020100 and XDB30000000, to Q.D.). F.J.G.d.A. acknowledges the ERC (Advanced grant no. 789104-eNANO), the Spanish MICINN (PID2020-112625GB-I00 and SEV2015-0522) and the CAS President’s International Fellowship Initiative for 2021. S.F. acknowledges the support of the US Department of Energy (grant no. DE-FG02-07ER46426). Z.S. acknowledges the Academy of Finland (grant nos. 314810, 333982, 336144 and 336818), The Business Finland (ALDEL), the Academy of Finland Flagship Programme (320167, PREIN), the European Union’s Horizon 2020 research and innovation program (820423, S2QUIP and 965124, FEMTOCHIP), the EU H2020-MSCA-RISE-872049 (IPN-Bio) and the ERC (834742). P.L. acknowledges the National Natural Science Foundation of China (grant no. 62075070).
Author information
Authors and Affiliations
Contributions
Q.D., R.Y., H.H. and F.J.G.d.A. conceived the idea. Q.D., F.J.G.d.A. and S.F. supervised the project. H.H. and N.C. led the experiments. R.Y., H.T. and F.J.G.d.A. developed the theory and performed the simulations. H.H. and N.C. prepared the samples and performed the near-field measurements. H.H., R.Y., N.C. and H.T. analysed the data, and all authors discussed the results. R.Y. and H.H. wrote the manuscript with input and comments from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Nanotechnology thanks Min Seok Jang, Alex Krasnok and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–31.
Source data
Source Data Fig. 3
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, H., Chen, N., Teng, H. et al. Doping-driven topological polaritons in graphene/α-MoO3 heterostructures. Nat. Nanotechnol. 17, 940–946 (2022). https://doi.org/10.1038/s41565-022-01185-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-022-01185-2
This article is cited by
-
Functional nanoporous graphene superlattice
Nature Communications (2024)
-
Tunable anisotropic van der Waals films of 2M-WS2 for plasmon canalization
Nature Communications (2024)
-
Steering and cloaking of hyperbolic polaritons at deep-subwavelength scales
Nature Communications (2024)
-
Plasmons in the Kagome metal CsV3Sb5
Nature Communications (2024)
-
Van der Waals quaternary oxides for tunable low-loss anisotropic polaritonics
Nature Nanotechnology (2024)