Abstract
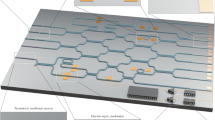
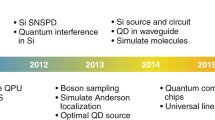
The scale-up of quantum hardware is fundamental to realize the full potential of quantum technology. Among a plethora of hardware platforms, photonics stands out: it provides a modular approach where the main challenges lie in the construction of high-quality building blocks and in the development of methods to interface the modules. The subsequent scale-up could exploit mature integrated photonics foundry technology to produce small-footprint quantum processors of immense complexity. Solid-state quantum emitters can realize a deterministic photon–emitter interface and enable key quantum photonic resources and functionalities, including on-demand single- and multi-photon-entanglement sources, as well as photon–photon nonlinear quantum gates. In this Review, we use the example of quantum dot devices to present the physics of deterministic photon–emitter interfaces, including the main photonic building blocks required to scale up, and discuss quantitative performance benchmarks. While our focus is on quantum dot devices, the presented methods also apply to other quantum-emitter platforms such as atoms, vacancy centres, molecules and superconducting qubits. We also identify applications within quantum communication and computing, presenting a route towards photonics with a genuine quantum advantage.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Aharonovich, I., Englund, D. & Toth, M. Solid-state single-photon emitters. Nat. Photon. 10, 631–641 (2016).
Blais, A., Grimsmo, A. L., Girvin, S. & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005 (2021).
Senellart, P., Solomon, G. & White, A. G. High-performance semiconductor quantum-dot single-photon sources. Nat. Nanotechnol. 12, 1026–1039 (2017).
Wang, H. et al. Towards optimal single-photon sources from polarized microcavities. Nat. Photon. 13, 770–775 (2019).
Uppu, R. et al. Scalable integrated single-photon source. Sci. Adv. 6, eabc8268 (2020). Scalable implementation of single-photon sources, providing a route to realizing quantum advantage.
Tomm, N. et al. A bright and fast source of coherent single photons. Nat. Nanotechnol. 16, 399–403 (2021).
Rudolph, T. Why I am optimistic about the silicon-photonic route to quantum computing. APL Photon. 2, 030901 (2017).
Lodahl, P., Mahmoodian, S. & Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 87, 347 (2015).
Kuhlmann, A. V. et al. Charge noise and spin noise in a semiconductor quantum device. Nat. Phys. 9, 570–575 (2013).
Kuhlmann, A. V. et al. Transform-limited single photons from a single quantum dot. Nat. Commun. 6, 8204 (2015). Demonstration of transform-limited photon emission with a quantum dot source.
Pedersen, F. T. et al. Near transform-limited quantum dot linewidths in a broadband photonic crystal waveguide. ACS Photon. 7, 2343–2349 (2020).
Dreeßen, C. L. et al. Suppressing phonon decoherence of high performance single-photon sources in nanophotonic waveguides. Quantum Sci. Technol. 4, 015003 (2018).
Santori, C., Fattal, D., Vučković, J., Solomon, G. S. & Yamamoto, Y. Indistinguishable photons from a single-photon device. Nature 419, 594–597 (2002).
Huthmacher, L. et al. Coherence of a dynamically decoupled quantum-dot hole spin. Phys. Rev. B 97, 241413 (2018).
Stockill, R. et al. Quantum dot spin coherence governed by a strained nuclear environment. Nat. Commun. 7, 12745 (2016).
Benson, O., Santori, C., Pelton, M. & Yamamoto, Y. Regulated and entangled photons from a single quantum dot. Phys. Rev. Lett. 84, 2513 (2000).
Liu, J. et al. A solid-state source of strongly entangled photon pairs with high brightness and indistinguishability. Nat. Nanotechnol. 14, 586–593 (2019).
Greilich, A., Carter, S. G., Kim, D., Bracker, A. S. & Gammon, D. Optical control of one and two hole spins in interacting quantum dots. Nat. Photon. 5, 702–708 (2011).
Grim, J. Q. et al. Scalable in operando strain tuning in nanophotonic waveguides enabling three-quantum-dot superradiance. Nat. Mater. 18, 963–969 (2019).
Krizek, F. et al. Field effect enhancement in buffered quantum nanowire networks. Phys. Rev. Mater. 2, 093401 (2018).
Sun, C. et al. Single-chip microprocessor that communicates directly using light. Nature 528, 534–538 (2015).
Bogaerts, W. et al. Programmable photonic circuits. Nature 586, 207–216 (2020).
Shaikh, F. K., Zeadally, S. & Exposito, E. Enabling technologies for green internet of things. IEEE Syst. J. 11, 983–994 (2015).
Morley, J., Widdicks, K. & Hazas, M. Digitalisation, energy and data demand: the impact of internet traffic on overall and peak electricity consumption. Energy Res. Soc. Sci. 38, 128–137 (2018).
Wootters, W. K. & Zurek, W. H. A single quantum cannot be cloned. Nature 299, 802–803 (1982).
Elshaari, A. W., Pernice, W., Srinivasan, K., Benson, O. & Zwiller, V. Hybrid integrated quantum photonic circuits. Nat. Photon. 14, 285–298 (2020).
Kim, J.-H., Aghaeimeibodi, S., Carolan, J., Englund, D. & Waks, E. Hybrid integration methods for on-chip quantum photonics. Optica 7, 291–308 (2020).
Antón, C. et al. Interfacing scalable photonic platforms: solid-state based multi-photon interference in a reconfigurable glass chip. Optica 6, 1471–1477 (2019).
Wan, N. H. et al. Large-scale integration of artificial atoms in hybrid photonic circuits. Nature 583, 226–231 (2020).
Zanin, G. L. et al. Fiber-compatible photonic feed-forward with 99% fidelity. Opt. Express 29, 3425–3437 (2021).
Hadfield, R. H. Single-photon detectors for optical quantum information applications. Nat. Photon. 3, 696–705 (2009).
Cohen, J. D., Meenehan, S. M. & Painter, O. Optical coupling to nanoscale optomechanical cavities for near quantum-limited motion transduction. Opt. Express 21, 11227–11236 (2013).
Ding, Y., Peucheret, C., Ou, H. & Yvind, K. Fully etched apodized grating coupler on the SOI platform with -0.58 dB coupling efficiency. Opt. Lett. 39, 5348–5350 (2014).
Tiecke, T. G. et al. Efficient fiber-optical interface for nanophotonic devices. Optica 2, 70–75 (2015).
Lenzini, F. et al. Active demultiplexing of single photons from a solid-state source. Laser Photon. Rev. 11, 1600297 (2017).
Papon, C. et al. Nanomechanical single-photon routing. Optica 6, 524–530 (2019). Demonstration of single-photon routing with ultra-low-loss nanomechanical transducer.
Bauters, J. F. et al. Planar waveguides with less than 0.1 dB/m propagation loss fabricated with wafer bonding. Opt. Express 19, 24090–24101 (2011).
Li, G. et al. Ultralow-loss, high-density SOI optical waveguide routing for macrochip interconnects. Opt. Express 20, 12035–12039 (2012).
Zhang, M., Wang, C., Cheng, R., Shams-Ansari, A. & Lončar, M. Monolithic ultra-high-Q lithium niobate microring resonator. Optica 4, 1536–1537 (2017).
Wang, C. et al. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 562, 101–104 (2018).
He, M. et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photon. 13, 359–364 (2019).
Midolo, L., Schliesser, A. & Fiore, A. Nano-opto-electro-mechanical systems. Nat. Nanotechnol. 13, 11–18 (2018).
Haffner, C. et al. Nano-opto-electro-mechanical switches operated at CMOS-level voltages. Science 366, 860–864 (2019).
Seok, T. J., Kwon, K., Henriksson, J., Luo, J. & Wu, M. C. Wafer-scale silicon photonic switches beyond die size limit. Optica 6, 490–494 (2019).
Elshaari, A. W. et al. On-chip single photon filtering and multiplexing in hybrid quantum photonic circuits. Nat. Commun. 8, 379 (2017).
Elshaari, A. W. et al. Strain-tunable quantum integrated photonics. Nano Lett. 18, 7969–7976 (2018).
Zhou, X. et al. On-chip nanomechanical filtering of quantum-dot single-photon sources. Laser Photon. Rev. 14, 1900404 (2019).
Li, H. et al. Multispectral superconducting nanowire single photon detector. Opt. Express 27, 4727–4733 (2019).
Lee, H., Chen, T., Li, J., Painter, O. & Vahala, K. J. Ultra-low-loss optical delay line on a silicon chip. Nat. Commun. 3, 867 (2012).
Weber, J. H. et al. Two-photon interference in the telecom C-band after frequency conversion of photons from remote quantum emitters. Nat. Nanotechnol. 14, 23–26 (2019).
Wang, C. et al. Ultrahigh-efficiency wavelength conversion in nanophotonic periodically poled lithium niobate waveguides. Optica 5, 1438–1441 (2018).
Chang, L. et al. Heterogeneously integrated GaAs waveguides on insulator for efficient frequency conversion. Laser Photon. Rev. 12, 1800149 (2018).
Singh, A. et al. Quantum frequency conversion of a quantum dot single-photon source on a nanophotonic chip. Optica 6, 563–569 (2019).
You, L. Superconducting nanowire single-photon detectors for quantum information. Nanophotonics 9, 2673 – 2692 (2020).
Reddy, D. V., Nerem, R. R., Nam, S. W., Mirin, R. P. & Verma, V. B. Superconducting nanowire single-photon detectors with 98% system detection efficiency at 1550 nm. Optica 7, 1649–1653 (2020).
Zhang, W. et al. A 16-pixel interleaved superconducting nanowire single-photon detector array with a maximum count rate exceeding 1.5 GHz. IEEE Trans. Appl. Supercond. 29, 2200204 (2019).
Marsili, F. et al. Detecting single infrared photons with 93% system efficiency. Nat. Photon. 7, 210–214 (2013).
Korzh, B. et al. Demonstration of sub-3 ps temporal resolution with a superconducting nanowire single-photon detector. Nat. Photon. 14, 250–255 (2020).
Zhu, D. et al. A scalable multi-photon coincidence detector based on superconducting nanowires. Nat. Nanotechnol. 13, 596–601 (2018).
Harris, N. C. et al. Quantum transport simulations in a programmable nanophotonic processor. Nat. Photon. 11, 447–452 (2017).
Carolan, J. et al. Universal linear optics. Science 349, 711–716 (2015). Realization of programmable universal photonic-integrated circuit for quantum photonics.
Wang, H. et al. Boson sampling with 20 input photons and a 60-mode interferometer in a 1014-dimensional Hilbert space. Phys. Rev. Lett. 123, 250503 (2019).
Gimeno-Segovia, M., Shadbolt, P., Browne, D. E. & Rudolph, T. From three-photon Greenberger-Horne-Zeilinger states to ballistic universal quantum computation. Phys. Rev. Lett. 115, 020502 (2015). Proposal of architecture for realising universal photonic cluster state with single-photon sources.
Zhang, Q. et al. Demonstration of a scheme for the generation of ‘event-ready’ entangled photon pairs from a single-photon source. Phys. Rev. A 77, 062316 (2008).
Varnava, M., Browne, D. E. & Rudolph, T. How good must single photon sources and detectors be for efficient linear optical quantum computation? Phys. Rev. Lett. 100, 060502 (2008).
Barz, S., Cronenberg, G., Zeilinger, A. & Walther, P. Heralded generation of entangled photon pairs. Nat. Photon. 4, 553–556 (2010).
Li, J.-P. et al. Heralded nondestructive quantum entangling gate with single-photon sources. Phys. Rev. Lett. 126, 140501 (2021).
Salter, C. et al. An entangled-light-emitting diode. Nature 465, 594–597 (2010).
Basset, F. B. et al. Quantum key distribution with entangled photons generated on demand by a quantum dot. Sci. Adv. 7, eabe6379 (2021).
Prilmüller, M. et al. Hyperentanglement of photons emitted by a quantum dot. Phys. Rev. Lett. 121, 110503 (2018).
Sheng, Y.-B. & Deng, F.-G. Deterministic entanglement purification and complete nonlocal Bell-state analysis with hyperentanglement. Phys. Rev. A 81, 032307 (2010).
Gershoni, D. A quantum knitting machine generating on demand cluster states of entangled photons. In Conference on Lasers and Electro-Optics (CLEO) FTu3H–3 (Optical Society of America, 2018).
Gao, W., Fallahi, P., Togan, E., Miguel-Sánchez, J. & Imamoglu, A. Observation of entanglement between a quantum dot spin and a single photon. Nature 491, 426–430 (2012).
Schwartz, I. et al. Deterministic generation of a cluster state of entangled photons. Science 354, 434–437 (2016). Demonstration of multi-photon entanglement with a quantum dot source.
Tiurev, K. et al. High-fidelity multi-photon-entangled cluster state with solid-state quantum emitters in photonic nanostructures. Preprint at https://arxiv.org/abs/2007.09295 (2020).
Briegel, H. J., Browne, D. E., Dür, W., Raussendorf, R. & Van den Nest, M. Measurement-based quantum computation. Nat. Phys. 5, 19–26 (2009).
Economou, S. E., Lindner, N. & Rudolph, T. Optically generated 2-dimensional photonic cluster state from coupled quantum dots. Phys. Rev. Lett. 105, 093601 (2010).
Pichler, H., Choi, S., Zoller, P. & Lukin, M. D. Universal photonic quantum computation via time-delayed feedback. Proc. Natl Acad. Sci. USA 114, 11362–11367 (2017).
Mahmoodian, S., Lodahl, P. & Sørensen, A. S. Quantum networks with chiral-light–matter interaction in waveguides. Phys. Rev. Lett. 117, 240501 (2016).
Le Jeannic, H. et al. Experimental reconstruction of the few-photon nonlinear scattering matrix from a single quantum dot in a nanophotonic waveguide. Phys. Rev. Lett. 126, 023603 (2021).
Javadi, A. et al. Spin–photon interface and spin-controlled photon switching in a nanobeam waveguide. Nat. Nanotechnol. 13, 398–403 (2018).
Chang, D. E., Sørensen, A. S., Demler, E. A. & Lukin, M. D. A single-photon transistor using nanoscale surface plasmons. Nat. Phys. 3, 807–812 (2007).
Braunstein, S. L. & van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Acín, A. et al. Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 98, 230501 (2007).
Kołodyński, J. et al. Device-independent quantum key distribution with single-photon sources. Quantum 4, 260 (2020).
Herrero-Collantes, M. & Garcia-Escartin, J. C. Quantum random number generators. Rev. Mod. Phys. 89, 015004 (2017).
Liu, Y. et al. Device-independent quantum random-number generation. Nature 562, 548–551 (2018).
Sangouard, N., Simon, C., De Riedmatten, H. & Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33 (2011).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).
Heshami, K. et al. Quantum memories: emerging applications and recent advances. J. Mod. Opt. 63, 2005–2028 (2016).
Fowler, A. G. et al. Surface code quantum communication. Phys. Rev. Lett. 104, 180503 (2010).
Buterakos, D., Barnes, E. & Economou, S. E. Deterministic generation of all-photonic quantum repeaters from solid-state emitters. Phys. Rev. X 7, 041023 (2017).
Borregaard, J. et al. One-way quantum repeater based on near-deterministic photon-emitter interfaces. Phys. Rev. X 10, 021071 (2020). Proposal of a one-way quantum repeater based on deterministic photon-emitter interfaces.
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018).
Sparrow, C. et al. Simulating the vibrational quantum dynamics of molecules using photonics. Nature 557, 660–667 (2018). Proof-of-concept quantum simulation of vibrational dynamics with single photons.
Cao, Y. et al. Quantum chemistry in the age of quantum computing. Chem. Rev. 119, 10856–10915 (2019).
Henriksen, N. E. & Hansen, F. Y. Theories of Molecular Reaction Dynamics: The Microscopic Foundation of Chemical Kinetics (Oxford Univ. Press, 2018).
Cao, Y., Romero, J. & Aspuru-Guzik, A. Potential of quantum computing for drug discovery. IBM J. Res. Dev. 62, 6:1–6:20 (2018).
Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).
Biamonte, J. et al. Quantum machine learning. Nature 549, 195–202 (2017).
Steinbrecher, G. R., Olson, J. P., Englund, D. & Carolan, J. Quantum optical neural networks. npj Quantum Inf. 5, 60 (2019).
Raussendorf, R. & Briegel, H. J. A one-way quantum computer. Phys. Rev. Lett. 86, 5188 (2001).
Walther, P. et al. Experimental one-way quantum computing. Nature 434, 169–176 (2005). Proof-of-concept demonstration of one-way quantum computing.
Witthaut, D., Lukin, M. D. & Sørensen, A. S. Photon sorters and qnd detectors using single photon emitters. Europhys. Lett. 97, 50007 (2012).
Gangloff, D. A. et al. Quantum interface of an electron and a nuclear ensemble. Science 364, 62–66 (2019).
Akopian, N., Wang, L., Rastelli, A., Schmidt, O. & Zwiller, V. Hybrid semiconductor-atomic interface: slowing down single photons from a quantum dot. Nat. Photon. 5, 230–233 (2011).
Meyer, H. M. et al. Direct photonic coupling of a semiconductor quantum dot and a trapped ion. Phys. Rev. Lett. 114, 123001 (2015).
Tsaturyan, Y., Barg, A., Polzik, E. S. & Schliesser, A. Ultracoherent nanomechanical resonators via soft clamping and dissipation dilution. Nat. Nanotechnol. 12, 776–783 (2017).
Monroe, C. & Kim, J. Scaling the ion trap quantum processor. Science 339, 1164–1169 (2013).
Mirhosseini, M., Sipahigil, A., Kalaee, M. & Painter, O. Superconducting qubit to optical photon transduction. Nature 588, 599–603 (2020).
Elfving, V. E., Das, S. & Sørensen, A. S. Enhancing quantum transduction via long-range waveguide-mediated interactions between quantum emitters. Phys. Rev. A 100, 053843 (2019).
Hummel, T. et al. Efficient demultiplexed single-photon source with a quantum dot coupled to a nanophotonic waveguide. Appl. Phys. Lett. 115, 021102 (2019).
Palacios-Berraquero, C., Mueck, L. & Persaud, D. M. Instead of ‘supremacy’ use ‘quantum advantage’. Nature 576, 213 (2019).
Preskill, J. Quantum entanglement and quantum computing. In Proc. 25th Solvay Conference on Physics (ed. Gross, D., Henneaux, M. & Sevrin, A.) 63–80 (World Scientific, 2013).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Aaronson, S. & Arkhipov, A. The computational complexity of linear optics. In Proc. 43rd Annual ACM Symposium on Theory of Computing 333–342 (ACM, 2011).
Zhong, H.-S. et al. Quantum computational advantage using photons. Science 370, 1460–1463 (2020). Photonic boson sampling experiment demonstrating quantum advantage with squeezed light sources.
Shchesnovich, V. S. Tight bound on the trace distance between a realistic device with partially indistinguishable bosons and the ideal boson sampling. Phys. Rev. A 91, 063842 (2015).
Acknowledgements
We thank S. Paesani for constructive comments on the manuscript. We gratefully acknowledge financial support from Danmarks Grundforskningsfond (DNRF 139, Hy-Q Center for Hybrid Quantum Networks).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
P.L. is founder of the start-up company Sparrow Quantum.
Additional information
Peer review information Nature Nanotechnology thanks Xinlun Cai, Roberto Osellame and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Uppu, R., Midolo, L., Zhou, X. et al. Quantum-dot-based deterministic photon–emitter interfaces for scalable photonic quantum technology. Nat. Nanotechnol. 16, 1308–1317 (2021). https://doi.org/10.1038/s41565-021-00965-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-021-00965-6
This article is cited by
-
Quantum key distribution using deterministic single-photon sources over a field-installed fibre link
npj Quantum Information (2024)
-
Light–matter interactions in quantum nanophotonic devices
Nature Reviews Physics (2024)
-
Mlora-CBF: efficient cluster-based routing protocol against resource allocation using modified location routing algorithm with cluster-based flooding
Wireless Networks (2024)
-
Heralded entanglement between error-protected logical qubits for fault-tolerant distributed quantum computing
Science China Physics, Mechanics & Astronomy (2024)
-
Deterministic photon source interfaced with a programmable silicon-nitride integrated circuit
npj Quantum Information (2023)