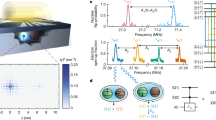
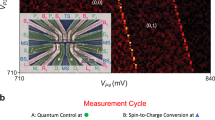
Abstract
Quantum entanglement is a fundamental property of coherent quantum states and an essential resource for quantum computing1. In large-scale quantum systems, the error accumulation requires concepts for quantum error correction. A first step toward error correction is the creation of genuinely multipartite entanglement, which has served as a performance benchmark for quantum computing platforms such as superconducting circuits2,3, trapped ions4 and nitrogen-vacancy centres in diamond5. Among the candidates for large-scale quantum computing devices, silicon-based spin qubits offer an outstanding nanofabrication capability for scaling-up. Recent studies demonstrated improved coherence times6,7,8, high-fidelity all-electrical control9,10,11,12,13, high-temperature operation14,15 and quantum entanglement of two spin qubits9,11,12. Here we generated a three-qubit Greenberger–Horne–Zeilinger state using a low-disorder, fully controllable array of three spin qubits in silicon. We performed quantum state tomography16 and obtained a state fidelity of 88.0%. The measurements witness a genuine Greenberger–Horne–Zeilinger class quantum entanglement that cannot be separated into any biseparable state. Our results showcase the potential of silicon-based spin qubit platforms for multiqubit quantum algorithms.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
All data in this study are available from the Zenodo repository at https://doi.org/10.5281/zenodo.4722605. Source data are provided with this paper.
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Dicarlo, L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574–578 (2010).
Neeley, M. et al. Generation of three-qubit entangled states using superconducting phase qubits. Nature 467, 570–573 (2010).
Häffner, H. et al. Scalable multiparticle entanglement of trapped ions. Nature 438, 643–646 (2005).
Neumann, P. et al. Multipartite entanglement among single spins in diamond. Science 323, 1326–1330 (2009).
Pla, J. J. et al. A single-atom electron spin qubit in silicon. Nature 489, 541–544 (2012).
Pla, J. J. et al. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334–338 (2013).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 9, 981–985 (2014).
Zajac, D. M. et al. Resonantly driven CNOT gate for electron spins. Science 359, 439–442 (2018).
Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotechnol. 13, 102–106 (2018).
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).
Huang, W. et al. Fidelity benchmarks for two-qubit gates in silicon. Nature 569, 532–536 (2019).
Yang, C. H. et al. Silicon qubit fidelities approaching incoherent noise limits via pulse engineering. Nat. Electron. 2, 151–158 (2019).
Yang, C. H. et al. Silicon quantum processor unit cell operation above one Kelvin. Nature 580, 350–354 (2020).
Petit, L. et al. Universal quantum logic in hot silicon qubits. Nature 580, 355–359 (2020).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Vandersypen, L. M. K. et al. Interfacing spin qubits in quantum dots and donors—hot, dense, and coherent. npj Quantum Inf. 3, 34 (2017).
Veldhorst, M., Eenink, H. G. J., Yang, C. H. & Dzurak, A. S. Silicon CMOS architecture for a spin-based quantum computer. Nat. Commun. 8, 1766 (2017).
Yoneda, J. et al. Quantum non-demolition readout of an electron spin in silicon. Nat. Commun. 11, 1144 (2020).
Xue, X. et al. Repetitive quantum non-demolition measurement and soft decoding of a silicon spin qubit. Phys. Rev. X 10, 021006 (2020).
Qiao, H. et al. Coherent multi-spin exchange coupling in a quantum-dot spin chain. Phys. Rev. X 10, 31006 (2020).
Zajac, D. M., Hazard, T. M., Mi, X., Nielsen, E. & Petta, J. R. Scalable gate architecture for densely packed semiconductor spin qubits. Phys. Rev. Appl. 6, 054013 (2016).
Angus, S. J., Ferguson, A. J., Dzurak, A. S. & Clark, R. G. Gate-defined quantum dots in intrinsic silicon. Nano Lett. 7, 2051–2055 (2007).
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004).
Sigillito, A. J., Gullans, M. J., Edge, L. F., Borselli, M. & Petta, J. R. Coherent transfer of quantum information in silicon using resonant SWAP gates. npj Quantum Inf. 5, 110 (2019).
Takeda, K., Noiri, A., Yoneda, J., Nakajima, T. & Tarucha, S. Resonantly driven singlet-triplet spin qubit in silicon. Phys. Rev. Lett. 124, 117701 (2020).
Tokura, Y., Van Der Wiel, W. G., Obata, T. & Tarucha, S. Coherent single electron spin control in a slanting Zeeman field. Phys. Rev. Lett. 96, 047202 (2006).
Takeda, K. et al. A fault-tolerant addressable spin qubit in a natural silicon quantum dot. Sci. Adv. 2, e1600694 (2016).
Borjans, F., Zajac, D. M., Hazard, T. M. & Petta, J. R. Single-spin relaxation in a synthetic spin–orbit field. Phys. Rev. Appl. 11, 044063 (2018).
Knill, E. et al. Randomized benchmarking of quantum gates. Phys. Rev. A 77, 012307 (2008).
Meunier, T., Calado, V. E. & Vandersypen, L. M. K. Efficient controlled-phase gate for single-spin qubits in quantum dots. Phys. Rev. B 83, 121403(R) (2011).
Martins, F. et al. Noise suppression using symmetric exchange gates in spin qubits. Phys. Rev. Lett. 116, 116801 (2016).
Reed, M. D. et al. Reduced sensitivity to charge noise in semiconductor spin qubits via symmetric operation. Phys. Rev. Lett. 116, 110402 (2016).
Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503 (2014).
Reed, M. D. et al. Realization of three-qubit quantum error correction with superconducting circuits. Nature 482, 382–385 (2012).
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015).
Mermin, N. D. Extreme quantum entanglement in a superposition of macroscopically distinct states. Phys. Rev. Lett. 65, 1838 (1990).
Connors, E. J., Nelson, J., Qiao, H., Edge, L. F. & Nichol, J. M. Low-frequency charge noise in Si/SiGe quantum dots. Phys. Rev. B 100, 165305 (2019).
Hendrickx, N. W. et al. A four-qubit germanium quantum processor. Nature 591, 580–585 (2021).
Mueller, F. et al. Printed circuit board metal powder filters for low electron temperatures. Rev. Sci. Instrum. 84, 044706 (2013).
Reilly, D. J., Marcus, C. M., Hanson, M. P. & Gossard, A. C. Fast single-charge sensing with a rf quantum point contact. Appl. Phys. Lett. 91, 162101 (2007).
Noiri, A. et al. Radio-frequency detected fast charge sensing in undoped silicon quantum dots. Nano Lett. 20, 947–952 (2020).
Andrews, R. W. et al. Quantifying error and leakage in an encoded Si/SiGe triple-dot qubit. Nat. Nanotechnol. 14, 747–750 (2019).
Hensgens, T. et al. Quantum simulation of a Fermi–Hubbard model using a semiconductor quantum dot array. Nature 548, 70–73 (2017).
Jones, A. M. et al. Spin-blockade spectroscopy of Si/Si–Ge quantum dots. Phys. Rev. Appl. 12, 014026 (2019).
Newville, M., Stensitzki, T., Allen, D. & Ingargiola, A. LMFIT: non-linear least-square minimization and curve-fitting for Python. Zenodo https://zenodo.org/record/11813#.YH6fbej7SUl (2014).
Jones, E., Oliphant, T. & Peterson, P. SciPy: open source scientific tools for Python. Science Open https://www.scienceopen.com/document?vid=ab12905a-8a5b-43d8-a2bb-defc771410b9 (2001).
Acknowledgements
We thank the Microwave Research Group at Caltech for technical support. This work was supported financially by Core Research for Evolutional Science and Technology (CREST), Japan Science and Technology Agency (JST) (JPMJCR15N2 and JPMJCR1675), MEXT Quantum Leap Flagship Program (MEXT Q-LEAP) grant no. JPMXS0118069228, JST Moonshot R&D grant no. JPMJMS2065 and JSPS KAKENHI grant nos. 16H02204, 17K14078, 18H01819, 19K14640 and 20H00237. T.N. acknowledges support from the Murata Science Foundation Research Grant and JST, PRESTO grant no. JPMJPR2017.
Author information
Authors and Affiliations
Contributions
K.T. and A.N. fabricated the device and performed the measurements. T.N., J.Y. and T.K. contributed the data acquisition and discussed the results. K.T. wrote the paper with inputs from all the co-authors. S.T. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Nanotechnology thanks Joseph Kerckhoff and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Initialization and measurement protocol.
Initialization and readout procedure. The spin readout and initialization for Q1 is performed near the (111)–(011) boundary, whereas for Q2 and Q3 it is performed near the (111)–(110) boundary. Note that Q2 cannot be directly read out through the reservoir as the co-tunnelling rate between the (111) and (101) states is too small compared to the spin relaxation rate \(T_1^{ - 1}\). The dwell times are 450 μs for Q3 initialization, 750 μs for Q1 initialization, 300 μs for Q3 readout and 750 μs for Q1 readout. The resonant SWAP pulses are 0.25 μs long and it corresponds to an exchange Rabi frequency of 2 MHz. The resonance frequency is typically around 410 MHz. The readout dwell time of Q3 is compromised for the finite T1 relaxation times of Q1 and Q2 and it results in imperfect spin-down initialization after the readout stage. Therefore, in order to increase the initialization fidelities, we use an explicit initialization stage which is redundant in the ideal case where all the three spins are initialized to spin-down after the readout stage.
Extended Data Fig. 2 Single-qubit characterization.
All qubits are initialized to spin-down before the manipulation stage and only one of the qubits is read out right after the manipulation stage unless noted. The exchange interactions are turned off. All errors represent the estimated standard errors for the best-fit values. a–d, T1 measurements. First, a spin-up state is prepared using an X pulse. Then we vary the waiting time of tw at the single-qubit manipulation point before performing single-shot measurement. In this T1 measurement, all three spins are sequentially read out and therefore the visibilities of Q1 and Q2 are decreased by T1 relaxation during the readout stage. Note that the visibility of Q3 is unaffected by the sequential readout. e–h, Ramsey interferometry measurements. First, a π/2 pulse (+2 MHz detuned from the resonance frequency) is applied to rotate the spin state to the xy-plane in the Bloch sphere. After an evolution time of tevol, another π/2 pulse is applied to project the spin state in the z-axis for measurement. The black solid curves are the fit with Gaussian decay. The integration time is 75.8 sec for all qubits. i–l, Hahn echo measurements. Each fitting curve is given by P↑(tevol) = Aexp(−(tevol/T2echo)γ) + B, where A and B are the constants to account for the readout fidelities and γ is an exponent. The exponents are found to be γ = 1.79 ± 0.12 (Q1), 2.75 ± 0.10 (Q2) and 2.61 ± 0.09 (Q3).
Extended Data Fig. 3 Additional randomized benchmarking measurements.
a, Measurement result with an asymmetric readout condition. F1 (F0) is the spin-up probability when the recovery Clifford gate is chosen so that the ideal final spin state is spin-up (-down). The data points at m = 0 are measured without any random Clifford gates applied. Only an X pulse is applied in the case of F1 and no pulse is applied in the case of F0. The dashed line shows a constant 0.462, the expected saturation value derived from the readout asymmetry. b, Measurement result with a more symmetric readout condition.
Extended Data Fig. 4 Randomized benchmarking with detuned microwave frequency.
a, Randomized benchmarking sequence for Q2 fidelity measurement. b, Randomized benchmarking measurement result of Q2 with a frequency detuning of 0.6 MHz. For each of the control bit (Q3) states, the measurement is performed for 16 sets of random Clifford gate sequences. The sequence fidelity shows an average of the results for the two control bit configurations. The errors represent the estimated standard errors for the best-fit values. c, d, Similar randomized benchmarking measurement performed for Q3. The errors represent the estimated standard errors for the best-fit values.
Extended Data Fig. 5 Measurements of exchange interactions.
All errors represent the estimated standard errors for the best-fit values. a, b, Controlled-rotation for Q1 and Q2. The measurement is performed to probe \(J_{12}^\prime\). First, Q1 and Q2 are initialized to spin-down. To prepare a spin-up control qubit (Q2) state, an X pulse is applied. After tuning on \(J_{12}^\prime\) by a gate voltage pulse, a low-power Gaussian microwave pulse (truncated at ±2σ) is applied to induce a controlled-rotation. The filled (open) circles show the measured spin-up probabilities with the control qubit spin-down (up). The solid lines are Gaussian fitting curves. From the separation of the two peaks, we obtain \(J_{12}^\prime\) = 2.75 ± 0.02 MHz. c, d, Similar controlled rotation measurement for Q2 and Q3. We obtain \(J_{23}^\prime\) = 12.50 ± 0.02 MHz from this measurement. e, Ramsey experiment to extract \(J_{12}^{{\mathrm{off}}}\). We perform two Ramsey measurements of Q1 with different control qubit (Q2) states. The difference of qubit frequency detuning is equivalent to \(J_{12}^{{\mathrm{off}}}\). f, Ramsey measurement result when Q2 is spin-down. The red circles are the measured Q1 spin-up probabilities and the black solid curve shows a fit with Gaussian decay. From the oscillation frequency of the decay curve, we extract δf↓ = 2.28 ± 0.01MHz. g, Measurement similar to the one in f when Q2 is spin-up. We extract δf↑ = 2.21 ± 0.01MHz. Since the difference between δf↓ and δf↑ is below the stochastic fluctuation of the frequency detuning, we conclude that \(J_{12}^{{\mathrm{off}}}\) is below our detection limit. Note that each frequency error shows one standard deviation of the fitting parameter. h–j, Ramsey experiments to extract \(J_{23}^{{\mathrm{off}}}\). We obtain \(J_{23}^{{\mathrm{off}}}\) = δf↑−δf↓ = 1.17 ± 0.01 MHz from these measurements.
Extended Data Fig. 6 Bell state tomography using Q2 and Q3.
As a benchmark of our two-qubit CZ gate, we perform Bell state tomography on Q2 and Q3. The experiment is a reduced version of the three-qubit GHZ state tomography. The readout errors are removed using the measured readout fidelities and maximum likelihood estimation is used to reconstruct the density matrices. a, Quantum gate sequence for Bell state creation and state tomography. By modifying the phase gates after the second CZ/2 pulse, we can create all four Bell states. b–e, Real parts of the measured density matrices for four Bell states, \(\Phi ^ + = (|{\uparrow \uparrow}\rangle + |{\downarrow \downarrow}\rangle )/\sqrt 2\) (b), \(\Phi ^ - = (|{\uparrow \uparrow}\rangle - |{\downarrow \downarrow} \rangle )/\sqrt 2\) (c), \(\Psi ^ + = (|{\downarrow \uparrow}\rangle + |{\downarrow \uparrow}\rangle)/\sqrt 2\) (d), and \(\Psi ^ - = (|{\downarrow \uparrow}\rangle - |{\uparrow \downarrow}\rangle)/\sqrt 2\) (e). We obtain the state fidelities relative to the target states of 0.942 (Φ+), 0.933 (Φ−), 0.950 (Ψ+) and 0.940 (Ψ−), and the concurrences of 0.950 (Φ+), 0.906 (Φ−), 0.923 (Ψ+) and 0.935 (Ψ−).
Extended Data Fig. 7 Imaginary part of the experimental GHZ state.
The imaginary part is all zero for an ideal GHZ state. Here, the maximum absolute value of the matrix elements is 0.09.
Source data
Source Data Fig. 1
Numerical data used to generate Fig. 1.
Source Data Fig. 2
Numerical data used to generate Fig. 2.
Source Data Fig. 3
Numerical data used to generate Fig. 3.
Source Data Extended Data Fig. 2
Numerical data used to generate Extended Data Fig. 2.
Source Data Extended Data Fig. 3
Numerical data used to generate Extended Data Fig. 3.
Source Data Extended Data Fig. 4
Numerical data used to generate Extended Data Fig. 4.
Source Data Extended Data Fig. 5
Numerical data used to generate Extended Data Fig. 5.
Source Data Extended Data Fig. 6
Numerical data used to generate Extended Data Fig. 6.
Source Data Extended Data Fig. 7
Numerical data used to generate Extended Data Fig. 7.
Rights and permissions
About this article
Cite this article
Takeda, K., Noiri, A., Nakajima, T. et al. Quantum tomography of an entangled three-qubit state in silicon. Nat. Nanotechnol. 16, 965–969 (2021). https://doi.org/10.1038/s41565-021-00925-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-021-00925-0
This article is cited by
-
Entangling gates on degenerate spin qubits dressed by a global field
Nature Communications (2024)
-
Design of high-performance entangling logic in silicon quantum dot systems with Bayesian optimization
Scientific Reports (2024)
-
Feedback-based active reset of a spin qubit in silicon
npj Quantum Information (2023)
-
Simultaneous single-qubit driving of semiconductor spin qubits at the fault-tolerant threshold
Nature Communications (2023)
-
Probing two-qubit capacitive interactions beyond bilinear regime using dual Hamiltonian parameter estimations
npj Quantum Information (2023)