Abstract
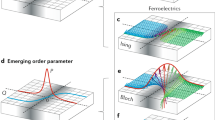
The driving force in materials to spontaneously form states with magnetic or electric order is of fundamental importance for basic research and device technology. The macroscopic properties and functionalities of these ferroics depend on the size, distribution and morphology of domains; that is, of regions across which such uniform order is maintained1. Typically, extrinsic factors such as strain profiles, grain size or annealing procedures control the size and shape of the domains2,3,4,5, whereas intrinsic parameters are often difficult to extract due to the complexity of a processed material. Here, we achieve this separation by building artificial crystals of planar nanomagnets that are coupled by well-defined, tuneable and competing magnetic interactions6,7,8,9. Aside from analysing the domain configurations, we uncover fundamental intrinsic correlations between the microscopic interactions establishing magnetically compensated order and the macroscopic manifestations of these interactions in basic physical properties. Experiment and simulations reveal how competing interactions can be exploited to control ferroic hallmark properties such as the size and morphology of domains, topological properties of domain walls or their thermal mobility.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the figures and other findings of this study can be found here (https://doi.org/10.3929/ethz-b-000429489).
Code availability
The programme codes that support the figures and other findings of this study can be found here (https://doi.org/10.3929/ethz-b-000429490). Additional data and information are available from the corresponding authors upon reasonable request.
References
Wadhawan, V. K. Introduction to Ferroic Materials (CRC Press, 2000).
Hubert, A. & Schäfer, R. Magnetic Domains: The Analysis of Magnetic Microstructures (Springer, 2009).
Seul, M. & Andelman, D. Domain shapes and patterns: the phenomenology of modulated phases. Science 267, 476–483 (1995).
Farztdinov, M. M. Structure of antiferromagnets. Sov. Phys. Uspekhi 7, 855–876 (1965).
Fiebig, M., Fröhlich, D., Leute, S. & Pisarev, R. V. Second harmonic spectroscopy and control of domain size in antiferromagnetic YMnO3. J. Appl. Phys. 83, 6560–6562 (1998).
Nisoli, C., Moessner, R. & Schiffer, P. Colloquium: artificial spin ice: designing and imaging magnetic frustration. Rev. Mod. Phys. 85, 1473–1490 (2013).
Heyderman, L. J. & Stamps, R. L. Artificial ferroic systems: novel functionality from structure, interactions and dynamics. J. Phys.: Condens. Matter 25, 363201 (2013).
Rougemaille, N. & Canals, B. Cooperative magnetic phenomena in artificial spin systems: spin liquids, Coulomb phase and fragmentation of magnetism – a colloquium. Eur. Phys. J. B. 92, 62 (2019).
Skjærvø, S. H., Marrows, C. H., Stamps, R. L. & Heyderman, L. J. Advances in artificial spin ice. Nat. Rev. Phys. 2, 13–28 (2020).
Kittel, C. Physical theory of ferromagnetic domains. Rev. Mod. Phys. 21, 541–583 (1949).
Sander, D. et al. The 2017 magnetism roadmap. J. Phys. D. Appl. Phys. 50, 363001 (2017).
Jungwirth, T. et al. The multiple directions of antiferromagnetic spintronics. Nat. Phys. 14, 200–203 (2018).
Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231–241 (2016).
Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587–590 (2016).
Gomonay, H. V. & Loktev, V. M. Shape-induced phenomena in finite-size antiferromagnets. Phys. Rev. B. 75, 174439 (2007).
Lehmann, J., Donnelly, C., Derlet, P. M., Heyderman, L. J. & Fiebig, M. Poling of an artificial magneto-toroidal crystal. Nat. Nanotechnol. 14, 141–144 (2019).
Luttinger, J. M. & Tisza, L. Theory of dipole interaction in crystals. Phys. Rev. 70, 954–964 (1946).
Kraemer, C. et al. Dipolar antiferromagnetism and quantum criticality in LiErF4. Science 336, 1416–1419 (2012).
Alkadour, B., Mercer, J. I., Whitehead, J. P., Southern, B. W. & van Lierop, J. Dipolar ferromagnetism in three-dimensional superlattices of nanoparticles. Phys. Rev. B. 95, 214407 (2017).
Sendetskyi, O. et al. Continuous magnetic phase transition in artificial square ice. Phys. Rev. B. 99, 214430 (2019).
Wang, R. F. et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 439, 303–306 (2006).
Ladak, S., Read, D. E., Perkins, G. K., Cohen, L. F. & Branford, W. R. Direct observation of magnetic monopole defects in an artificial spin-ice system. Nat. Phys. 6, 359–363 (2010).
Mengotti, E. et al. Real-space observation of emergent magnetic monopoles and associated dirac strings in artificial kagome spin ice. Nat. Phys. 7, 68–74 (2011).
Farhan, A. et al. Exploring hyper-cubic energy landscapes in thermally active finite artificial spin-ice systems. Nat. Phys. 9, 375–382 (2013).
Kapaklis, V. et al. Thermal fluctuations in artificial spin ice. Nat. Nanotechnol. 9, 514–519 (2014).
Anghinolfi, L. et al. Thermodynamic phase transitions in a frustrated magnetic metamaterial. Nat. Commun. 6, 8278 (2015).
Farhan, A. et al. Direct observation of thermal relaxation in artificial spin ice. Phys. Rev. Lett. 111, 057204 (2013).
Gliga, S. et al. Emergent dynamic chirality in a thermally driven artificial spin ratchet. Nat. Mater. 16, 1106–1111 (2017).
Loreto, R. P. et al. Emergence and mobility of monopoles in a unidirectional arrangement of magnetic nanoislands. Nanotechnology 26, 295303 (2015).
Arnalds, U. B. et al. A new look on the two-dimensional Ising model: thermal artificial spins. N. J. Phys. 18, 023008 (2016).
Morgan, J. P., Stein, A., Langridge, S. & Marrows, C. H. Thermal ground-state ordering and elementary excitations in artificial magnetic square ice. Nat. Phys. 7, 75–79 (2011).
Nisoli, C. On thermalization of magnetic nano-arrays at fabrication. N. J. Phys. 14, 035017 (2012).
Mól, L. A. et al. Magnetic monopole and string excitations in two-dimensional spin ice. J. Appl. Phys. 106, 063913 (2009).
Bortz, A., Kalos, M. & Lebowitz, J. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Computational Phys. 17, 10–18 (1975).
Acknowledgements
We thank T. Lottermoser, S. Vélez Centoral, A. Cano and T. Weber for discussions. M.F. acknowledges funding by the Swiss National Science Foundation (project no. 200021-175926). J.L. and M.F. acknowledge funding by the ETH Research grant no. ETH-28 14-1 ‘Resonant optical magnetoelectric effect in magnetic nanostructures’. A.B. and M.F. acknowledge funding by the European Research Council (advanced grant no. 694955–INSEETO). N.L. and L.J.H. acknowledge funding by the Swiss National Science Foundation (project no. 200021-155917).
Author information
Authors and Affiliations
Contributions
All authors contributed to the discussion and interpretation of the study. J.L., A.B. and M.F. wrote the manuscript with input from all coauthors. C.D. and N.L. fabricated the nanomagnetic structures. J.L. performed magnetic force microscopy experiments. A.B. and P.M.D. performed the Monte Carlo simulations. M.F. and L.J.H. supervised the study.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Nanotechnology thanks Will Branford, Olena Gomonay and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Lehmann, J., Bortis, A., Derlet, P.M. et al. Relation between microscopic interactions and macroscopic properties in ferroics. Nat. Nanotechnol. 15, 896–900 (2020). https://doi.org/10.1038/s41565-020-0763-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-020-0763-9
This article is cited by
-
Selectively designed Fe doping of lead-free BaTiO3 piezoceramics
Journal of Materials Science: Materials in Electronics (2022)